
Linear Subset Size Scheduling for Many-objective Optimization
using NSGA-II based on Pareto Partial Dominance
Makoto Ohki
Field of Technology, Tottori University,
4, 101 Koyama-Minami, Tottori, Tottori 680-8552, Japan
Keywords:
Many-Objective Evolutionary Algorithm, Pareto Partial Dominance, Subset Size Scheduling, NSGA-II,
0/1 Knapsack Problem.
Abstract:
This paper describes techniques for improving the solution search performance of a multi-objective evolution-
ary algorithm (MOEA) in many-objective optimization problems (MaOP). As an MOEA for MaOP, we focus
on NSGA-II based on Pareto partial dominance. NSGA-II based on Pareto partial dominance requires before-
hand a combination list of the number of objective functions to be used for Pareto partial dominance. More-
over, the contents of the combination list greatly influence the optimization result. We propose to schedule a
parameter r meaning the subset size of objective functions for Pareto partial dominance. This improvement not
only releases users from the schedule of the parameter r but also improves the convergence to Pareto optimal
solutions (P OS) and the diversity of the individual set obtained by the optimization. Moreover, we propose
to kill individuals of the archive set, where the individuals have the same contents as the individual created
by the mating. This improvement excludes individuals with the same contents which obtained relatively good
evaluations. The improved technique and other conventional techniques are applied to a many-objective 0/1
knapsack problem for verification of the effectiveness.
1 INTRODUCTION
In the real world, there are many problems with
more than four objectives. Such the multi-objective
optimization problems (MOP) with objective num-
ber of four or more are called many-objective op-
timization problem (MaOP). MaOP is difficult to
solve and is tackled by many researchers (Zitzler
and Thiele, 1998; Zitzler, 1999; Zitzler et al., 2001;
Deb et al., 2000; Deb, 2001; Coello et al., 2007).
Although SPEA2 (Zitzler and Thiele, 1998; Zitzler,
1999; Zitzler et al., 2001) and NSGA-II (Deb et al.,
2000; Deb, 2001) are well known as powerful al-
gorithm for MOPs, they do not work so effectively
for MaOPs (Purshouse and Fleming, 2003; Hughes,
2005; Aguirre and Tanaka, 2007). In this paper, we
handle the case of solving an MaOP by NSGA-II
based algorithm.
When applying NSGA-II or SPEA2 to MaOP, as
the objective number increases, most of the solutions
in the solution set, or population, become a relation
that is not superior or inferior to each other. This re-
lation is called non-dominated (ND) relationship. As
a result, the convergence of the obtained set of Pareto
Optimal Solutions (P OS) to the optimum Pareto front
remarkably decreases. Sato et al. have proposed a
Pareto partial dominance that makes it easier to deter-
mine the superiority/inferiority relationship between
solutions by using several objective functions instead
of all objective functions as an algorithm for such
MaOP (Sato et al., 2010). Since NSGA-II based on
Pareto partial dominance focuses on a relatively small
number of objectives, solutions are easy to decide su-
periority/inferiority even on MaOP, and an effective
selection pressure can be expected.
NSGA-II based on Pareto partial dominance has
the following three problems. The first problem is
that a combination list of the number of objects to
be used for Pareto partial dominance must be speci-
fied before the optimization. The second one is that
an appropriate number of selected objectives accord-
ing to the complexity of the problem in undecided.
Moreover, the contents of the combination list greatly
influence the optimization result. NSGA-II based on
Pareto partial dominance performs ND sorting using
all objective functions at a specific generation cycle,
and preserves parents as an archive set for the next
generation. This process generates child individuals
Ohki, M.
Linear Subset Size Scheduling for Many-objective Optimization using NSGA-II based on Pareto Partial Dominance.
DOI: 10.5220/0006905402770283
In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 1, pages 277-283
ISBN: 978-989-758-321-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
277

having the same contents as the already existing indi-
vidual in the archive set in some cases. As a result, the
same individuals increases in the first front set, which
disturbs effective ranking in the front selection. This
is the third problem. By consideration of these prob-
lems, this paper proposes a simple scheduling tech-
nique of partial objective set used for Pareto partial
dominance and a technique of killing individuals hav-
ing the same contents in preserving the archive set. In
order to verify the effectiveness of the proposed tech-
niques, we examine a many-objective 0/1 knapsack
problem(Zitzler and Thiele, 1998).
2 MANY-OBJECTIVE
OPTIMIZATION PROBLEM
MOP is a problem that optimizes, or maximizes in
this paper, multiple objective functions under several
constraints. Since the objective functions are in a
trade-off relationship with each other, it is not pos-
sible, in general, to obtain the only one solution that
completely satisfies all the objective functions. There-
fore, we require to obtain P OS of compromised solu-
tions without superiority or inferiority to each other.
For the objective function vector f consisting m objec-
tive functions, f
i
, the problem of finding the variable
vector x that maximizes the value of f
i
in the feasible
region S in the solution space is defined as follows.
max. f(x) = [ f
1
(x), f
2
(x),··· , f
m
(x)]
T
s.t. x ∈ S
(1)
When the values of the objective function, f
i
, of two
solutions x and y satisfy the following relation, we say
that the solution x dominates the solution y.
f(x) f(y) ,
∀i ∈ M : f
i
(x) = f
i
(y) ∧ ∃i ∈ M : f
i
(y) > f
i
(y) (2)
where M denotes a set of the indexes for the objec-
tive function, {1,2,..., m}. When there is no solu-
tion dominates a solution x, the solution x is called
non-inferior solution. A set of such the non-inferior
solutions is defined as the following P OS.
P OS = {x ∈ S|¬∃y ∈ S.f(y) f(x)} (3)
A Pareto front showing the the trade-off relation be-
tween the objective functions is defined as follows.
F ront = {f(x)|x ∈ P OS} (4)
Several effective studies (Zitzler and Thiele, 1998;
Zitzler, 1999; Zitzler et al., 2001; Deb et al., 2000;
Deb, 2001; Coello et al., 2007) have been made on
MOP as defined by Eq.(1). NSGA-II shown in Fig.1
is a powerful multi-objective optimization scheme as
a method proposed on one of these studies. NSGA-
II applies non-dominated sorting (ND sorting) to the
population Q, and the individuals are classified to sev-
eral ranked subsets, F
1
,F
2
,F
3
,· ··. While not exceed-
ing the size of the parent set P, the individuals of each
subset are moved to the parent set in order. Individ-
uals of the subset that exceeds the size of the parent
set is sorted using crowding distance (CD sorting) and
moved to the parent set. The individuals not selected
are culled. The mating operators generates the child
set C from the parent set P by using the crossover and
mutation operators.
Although NSGA-II effectively solves MOP with
less than four objective functions, as the objective
number m increases, an appropriate P OS could not be
obtained even by those methods containing the con-
ventional NSGA-II. When ND is performed based on
the conventional Pareto dominance using all m objec-
tive functions, as the number of objective function in-
creases, a subset of solutions satisfying Eq.(2) is dif-
ficult to obtain (Tsuchida et al., 2009). Then most
solutions of the population become non-inferior solu-
tions. As a result, the superiority/inferiority relation-
ship between solutions is difficult to determined, and
the selection pressure in the optimization is signifi-
cantly reduced. This paper focuses to NSGA-II with
Pareto partial dominance shown in Fig.2 for solving
MaOP. Pareto partial dominance is based on a con-
cept of partially applying Pareto domination to r ob-
jective functions extracted from all m objective func-
tions. The Pareto partial dominance is defined by the
following formula.
f(x) A f(y) ,
∀i ∈ R ⊂ M : f
i
(x) = f
i
(y)
∧∃i ∈ R ⊂ M : f
i
(y) > f
i
(y) (5)
where R denotes a set of r indexes selected from M.
Since conditions satisfying Pareto partial dominance
are relaxed as compared with the conventional domi-
nance using all m objective functions, the population
is easier to rank finely in MaOP with large m.
Figure 1: The conventional NSGA-II.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
278

In NSGA-II based on Pareto partial dominance,
first of all, given r, the number of objective functions
to be considered in the partial ND sorting, a combi-
nation list of
m
C
r
selections is prepared beforehand.
For each I
g
generations, the combination of the ob-
jective functions to be considered for Pareto partial
dominance is changed, and R
g+1
is selected with per-
forming ND sorting on P
g
+C
g
+A using all m objec-
tive functions and copied to the archive set A, where
+ denotes the direct sum.
Figure 2: NSGA-II with Pareto partial dominance.
3 IMPROVEMENT OF NSGA-II
BASED ON PARETO PARTIAL
DOMINANCE
NSGA-II based on Pareto partial dominance has the
following three problems. The first problem is that
the subset size of the objective functions to be used
for Pareto partial dominance is required to beforehand
specify before the optimization in a form of a list, or
the combination list. The second one is that an appro-
priate value of the subset size according to the com-
plexity of the problem is unknown. The contents of
the combination list greatly influence the optimization
result. On the other hand, the creation of the combi-
nation list is a very troublesome and difficult task for
the user. NSGA-II based on Pareto partial dominance
performs ND sorting using all objective functions at
a specific generation cycle, and preserves parents as
an archive set for the next generation. This process
generates child individuals having the same contents
as the already existing individual in the archive set
in some cases. As a result, the same individuals in-
creases in the first front set, which disturbs effective
ranking in the front selection. This is the third prob-
lem. In order to avoid these problems, this paper pro-
poses two improvements. A block chart of the im-
proved NSGA-II based on Pareto partial dominance
is shown in Fig.3.
As the first improvement, a subset size scheduling
is proposed for NSGA-II based on Pareto partial dom-
inance. NSGA-II based on Pareto partial dominance
treated in this paper does not use the combination list
for each I
g
generation cycle. The parameter r is given
by the following equations.
q =
g · m
G
+ rand int(2B + 1) − B, (6)
r =
B, q < B
q, B 5 q < m
m, q = m
(7)
where m denotes the number of the objective func-
tions, rand int(·) denotes a function returns a random
integer less than the argument, B denotes an integer
parameter larger than 1 and less than m/2, and G de-
notes the end generation. Fig.4 shows the possible
value of the selection number, r.
Figure 3: Improved NSGA-II with Pareto partial domi-
nance.
In NSGA-II based on Pareto partial dominance,
several individuals having the same contents as an in-
dividual already existing in the children, C
t
, or the
archive set, A, are generated and stored by the mating.
If the optimization proceeds while sustaining such the
individuals having relatively good evaluation, dupli-
cates of them increases within the population. If the
problem to be optimized is relatively simple, individ-
uals with the same content arefrequently generated
during the optimization. The second improvement is
killing such the individuals having the same contents
of an individual already existing in the children, C
g
,
and the archive set, A, after the mating. Since the
optimization problem treated in this paper is the max-
imizing problem, by setting the value of all objective
functions of such the individual to 0, the individual
are killed. The same content individual become the
worst individual. After killing the same content indi-
vidual, the mating does not reproduce the individual.
Linear Subset Size Scheduling for Many-objective Optimization using NSGA-II based on Pareto Partial Dominance
279

Figure 4: The selection number, r, probablistically takes a
value on the colored range according to the generation g,
where rand int(·) denotes a function returns a random inte-
ger less than the argument, B denotes an integer parameter
larger than 1 and less than m/2, and G denotes the final
generation.
4 MANY-OBJECTIVE 0/1
KNAPSACK PROBLEM
In order to verify the effectiveness of the improved
technique, a many-objective 0/1 knapsack Problem
(MaOKSP) is performed. MaOKSP composed of m
knapsacks and j items. The capacity of the i-th knap-
sack is c
i
. The weight and the price of the j-th item
are w
i j
and p
i j
respectively in the i-th knapsack. Let
an individual x ∈ 0, 1
n
be the n dimensional vector
that selects the items. MaOKSP is defined by the fol-
lowing formula.
max. f(x) = [ f
1
(x), f
2
(x),· ·· , f
m
(x)]
T
s.t.
n
∑
j=1
w
i j
· x
j
5 c
i
(8)
f
i
(x) =
n
∑
j=1
p
i j
· x
j
for i = 1,2, ··· ,m (9)
P OS obtained by the optimization is evaluated by
using Maximum Spread (MS)(Zitzler, 1999) and
Norm(Sato et al., 2006).
MS expresses a measure showing the spread of
P OS distribution. On the other hand, Norm shows
a measure of the convergence to the optimal Pareto
front of P OS. These values are obtained by the fol-
lowing equations.
Norm(P OS) =
|
P OS
|
∑
j=1
s
m
∑
i=1
f
i
(x
j
)
2
|
P OS
|
(10)
MS(P OS) = (11)
s
m
∑
i=1
max
|
P OS
|
j=1
f
i
(x
j
) − min
|
P OS
|
j=1
f
i
(x
j
)
2
The conventional NSGA-II, NSGA-II based on Pareto
partial dominance when r = 3, r = 6 and r = 8,
NSGA-II based on Pareto partial dominance in the
case of giving the combination list shown in Table1
and the improved technique are carried out for the
verification. The optimization is performed by set-
ting the objective number to m = 4, 6,8, 10 and the
iterative generations to G = 1,000, 000.
Fig.5 shows transition of the number of individu-
als of the first-front according to the generation in the
case that m = 10 and I
g
= 500. In the figure, “NSGA-
II” denotes the results by the conventional NSGA-II,
“PPD(r=*)” denotes the results by NSGA-II based on
Pareto partial dominance with the constant value of
r = ∗, “PPD(list)” denotes the results by NSGA-II
based on Pareto partial dominace with the combina-
tion list shown in Table1, and “Improved” denotes the
results by the algorithm proposed in this paper. The
conventional NSGA-II and NSGA-II based on Pareto
partial dominance in r = 8 has given large number
of the individuals of the first-front set throughout the
optimization. NSGA-II based on Pareto partial domi-
nance with r = 6 has given the number next to them.
At the end of the optimization, the improved tech-
nique has caught up with these values. NSGA-II
based on Pareto partial dominance with the combi-
nation list is also similar.
Fig.6 shows Norm values values after the opti-
mization to the objective number m in the case that
I
g
= 500. In any technique, the convergence to
P OS increases as the number of objectives increases.
Although, regarding to the convergence, NSGA-II
based on Pareto partial dominance in the case that
r = 3, NSGA-II based on Pareto partial dominance
with the combination list and the improved technique
have given almost equivalent results, the conventional
NSGA-II has given relatively poor results.
Fig.7 shows MS values values after the optimiza-
tion to the objective number m in the case that I
g
=
500. The MS value, or the diversity of P OS, given
by NSGA-II based on Pareto partial dominance in
Table 1: The combination list for NSGA-II based on Pareto
partial dominance.
generation range
0 500k 900k
−500k −900k −1M
m r
4 2 3 4
6 3 5 6
generation rage
0 300k 600k 900k
−300k −600k −900k −1M
m r
8 3 5 7 8
10 3 6 8 10
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
280

Figure 5: Transition of the number of individuals of the
first-front according to the generation.
the case that r = 3 decreases as the objective num-
ber increases, whereas it increases with the other three
techniques. In the improved technique, since r in-
creases as the generation progresses, the superior-
ity/inferiority relationship of solutions becomes dif-
ficult to decide by Pareto partial dominance at the end
of the optimization, and many individuals belong to
the first-front set. As a result, since most individu-
als of the parents are ranked by the CD sorting, and
it is considered that diversity has increased. NSGA-II
based on Pareto partial dominance with the combi-
nation list has shown diversity equal to or less than
that of the improved technique. The reason that suf-
ficient diversity has not been obtained by NSGA-II
Figure 6: Comparison of Norm values to the object number
m.
based on Pareto partial dominance in the case that
r = 3 is considered as because partial dominance by
using all objectives has not been performed only be-
tween 900,000-1 million generations. Regarding the
diversity of solutions, the conventional NSGA-II has
given the highest value.
Fig.8 shows Norm values to the generation g in
the case that m = 10 and I
g
= 500. In NSGA-II based
on Pareto partial dominance, the convergence to P OS
tends to decrease as the value of the parameter r in-
creases. In this technique, when r approaches m, the
solutions are hard to dominated by the partial domi-
nance, so a large number of individuals are selected
as the first-front set. As a result, sufficient ranking
is not made in the non-dominated sorting, and the
convergence has deteriorated. On the other hand, al-
though the improved technique has shown the highest
convergence at the beginning of the optimization, the
convergence has declined at the final stage. In the
improved technique, since the value of r increases as
the generation progresses, the solutions become hard
to dominated by the partial dominance. As a result,
sufficient ranking is not made in the non-dominated
sorting, and the convergence has deteriorated in the
final stage.
Fig.9 shows MS values to the generation g in the
case that m = 10 and I
g
= 500. Although the diversity
in the cases of the conventional NSGA-II and NSGA-
II based on Pareto partial dominance in r = 8, main-
tains a high value throughout, the convergence is low
as shown in Fig.8, so it is not necessary to pay atten-
tion to them. On the other hand, the diversity is ris-
ing as the optimization progress in the case of the im-
proved technique. Moreover, the improved technique
Figure 7: Comparison of MS values to the object number
m.
Linear Subset Size Scheduling for Many-objective Optimization using NSGA-II based on Pareto Partial Dominance
281
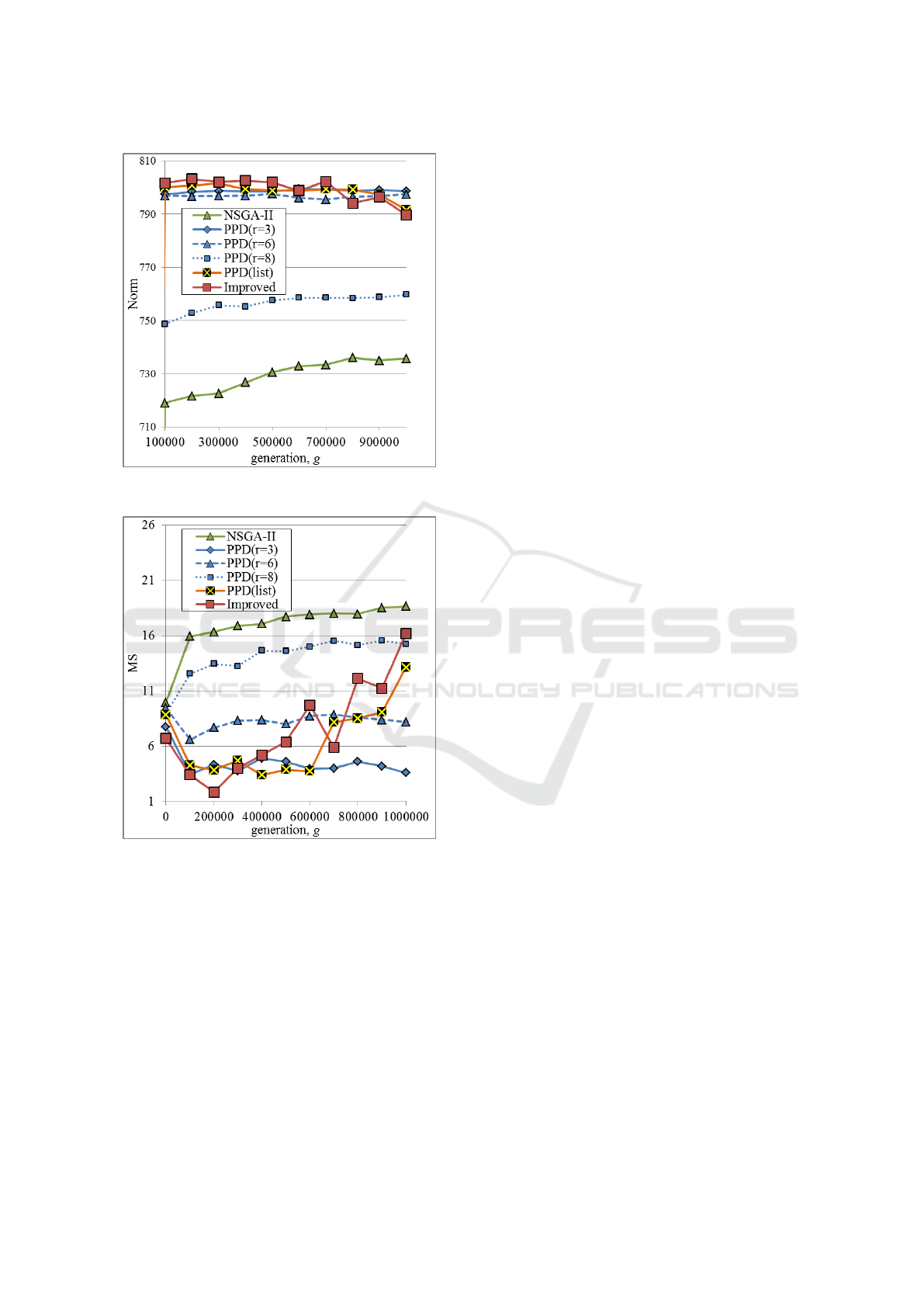
Figure 8: Comparison of the Norm values to the generation
g.
Figure 9: Comparison of the MS values to the generation g.
brings relatively high convergence as shown in Fig.8,
so that the superiority of the improved technique is
shown overall.
5 CONCLUSION
In this paper, the improvement of NSGA-II based
on Pareto partial dominance has been proposed with
the aim of improving the solution search performance
of MOEA for MaOP. In the improvement, we have
proposed the simple scheduling of the number r of
the objective functions for Pareto partial dominance
and killing the individuals of the archive set, where
the individual has the same contents as the individ-
ual created by the mating. The improved technique
and other conventional techniques are applied to the
many-objective 0/1 knapsack problem for verification
of the effectiveness. The improved technique has
given the higher diversity than other techniques as the
number of the objective functions of the problem in-
creases. On the other hand, the improved technique
has given the convergence equal to or higher than the
other techniques even when the number of the objec-
tive functions becomes large. By means of the pro-
posed simple scheduling of the parameter r, sufficient
convergence has been obtained in the early genera-
tions with the smaller r, and the diversity has been
supplemented in the generations with the larger r at
the end of the optimization.
Since the improved technique still has given in-
sufficient results in terms of the diversity, we need to
improve this point while maintaining the current con-
vergence. Although each technique has been applied
to the relatively simple many-objective 0/1 knapsack
problem in this paper, we need to apply to more com-
plicated problems and verify the effectiveness. And
we also need to pursue an optimal combination list
for NSGA-II based on Pareto partial dominance with
the selection list.
ACKNOWLEDGEMENTS
This research work has been supported by JSPS
KAKENHI Grant Number JP17K00339.
The author would like to thank to her families, the
late Miss Blackin’, Miss Blanc, Miss Caramel, Mr.
Civita, Miss Marron, Miss Markin’, Mr. Yukichi and
Mr. Ojarumaru, for bringing her daily healing and
good research environment.
REFERENCES
Aguirre, H. E. and Tanaka, K. (2007). Working princi-
ples, behavior, and performance of moeas on mnk-
landscapes. European Journal of Operational Re-
search, 181(3):1670–1690.
Coello, C. A. C., Lamont, G. B., Van Veldhuizen, D. A.,
et al. (2007). Evolutionary algorithms for solving
multi-objective problems, volume 5. Springer.
Deb, K. (2001). Multi-objective optimization using evolu-
tionary algorithms, volume 16. John Wiley & Sons.
Deb, K., Agrawal, S., Pratap, A., and Meyarivan, T. (2000).
A fast elitist non-dominated sorting genetic algorithm
for multi-objective optimization: Nsga-ii. In Interna-
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
282

tional Conference on Parallel Problem Solving From
Nature, pages 849–858. Springer.
Hughes, E. J. (2005). Evolutionary many-objective opti-
misation: many once or one many? In Evolutionary
Computation, 2005. The 2005 IEEE Congress on, vol-
ume 1, pages 222–227. IEEE.
Purshouse, R. C. and Fleming, P. J. (2003). Conflict, har-
mony, and independence: Relationships in evolution-
ary multi-criterion optimisation. In International Con-
ference on Evolutionary Multi-Criterion Optimiza-
tion, pages 16–30. Springer.
Sato, H., Aguirre, H. E., and Kiyoshi, T. (2010). Effects of
moea temporally switching pareto partial dominance
on many-objective 0/1 knapsack problems. Trans-
actions of the Japanese Society for Artificial Intelli-
gence, 25:320–331.
Sato, M., Aguirre, H. E., and Tanaka, K. (2006). Ef-
fects of δ-similar elimination and controlled elitism
in the nsga-ii multiobjective evolutionary algorithm.
In Evolutionary Computation, 2006. CEC 2006. IEEE
Congress on, pages 1164–1171. IEEE.
Tsuchida, K., Sato, H., Aguirre, H. E., and Tanaka, K.
(2009). Analysis of nsga-ii and nsga-ii with cdas,
and proposal of an enhanced cdas mechanism. JACIII,
13(4):470–480.
Zitzler, E. (1999). Evolutionary algorithms for multiobjec-
tive optimization: Methods and applications. Citeseer.
Zitzler, E., Laumanns, M., and Thiele, L. (2001). Spea2:
Improving the strength pareto evolutionary algorithm.
TIK-report, 103.
Zitzler, E. and Thiele, L. (1998). Multiobjective optimiza-
tion using evolutionary algorithms comparative case
study. In international conference on parallel prob-
lem solving from nature, pages 292–301. Springer.
Linear Subset Size Scheduling for Many-objective Optimization using NSGA-II based on Pareto Partial Dominance
283
