A Suboptimal Strategy for Autonomous Marine Vehicle Navigation

in Variable Sea Currents

Kangsoo Kim

National Maritime Research Institute, National Institute of Maritime, Port, and Aviation Technology,

6-38-1 Shinkawa, Mitaka, Tokyo 181-0004, Japan

Keywords: Suboptimal, Navigation, Uncertainty, Variable, Sea Current, Minimum-time, Marine Vehicle.

Abstract: A navigation strategy achieving suboptimality in the transits of autonomous marine vehicles is presented. The

objective of optimal navigation is the minimum-time transit of a marine vehicle moving in a flow field of sea

currents. Reactive revisions of an ongoing optimal navigation followed by tracking controls are the key

features of the proposed suboptimal strategy. In this research, a globally working numerical procedure for

obtaining the solution of an optimal heading guidance law is presented. The developed solution procedure

derives optimal heading reference that achieves the minimum-time transit of a marine vehicle in any

deterministic sea currents whether stationary or time varying. The proposed suboptimal navigation works as

a fail-safe strategy for the optimal navigation when there happen significant hostile actions which possibly

cause the failure in ongoing optimal navigation. Simplicity and robustness are notable characteristics of our

suboptimal strategy compared to others seeking rigorous optimality. Simulation results of autonomous

underwater vehicle routing conducted by suboptimal navigation in various sea currents are presented.

1 INTRODUCTION

The sea environment contains several kinds of flows

that significantly interact with the motion of surface

or submerged vessels. Among these, sea or ocean

currents are the most significant flow disturbances,

directly affecting the travelling speed, the power

consumption, and thus the endurance and range of a

vehicle. Suppose that a marine vehicle is to transit to

a given destination in a region of flow disturbance.

Then it is quite natural that the transit time of the

vehicle should change according to the selection of a

specific trajectory. When the power consumption of a

vehicle is controlled to be constant throughout the

transit, the travelling time is directly proportional to

the total energy consumption.

Recently, autonomous marine vehicles (AMVs) are

playing important roles in diverse applications, such

as oceanographic survey, marine patrol, undersea

oil/gas production, and various military applications

(Nicholson and Healey, 2008). Relying on an on-

board battery system as the main energy source,

endurance and moving range of an AMV are limited

by its power consumption, as well as its energy

capacity. Therefore, the minimum-time transit of an

AMV can achieve enhanced vehicle safety and

mission effectiveness (Kim and Ura, 2010).

Considerable research has been done on the optimal

guidance or path planning for a mobile vehicle

through a varied fluid environment. Though aiming at

the same objectives, the most notable difference

between the guidance and the path planning is the

consideration of dynamical constraints. While, in

general, dynamical constraints in vehicle motion are

incorporated into the formulation of vehicle guidance

problems (Crespo and Sun, 2001; Zhao and Bryson,

1990), they are ignored in most path planning

problems (Alvarez et. al, 2004; Papadakis and

Perakis, 1990). This allows great flexibility in the

target path generation, enabling the use of

combinatorial optimization techniques in path

planning approaches. Dynamic programming (DP)

might be one of the most classical and popular

techniques for combinatorial optimization. Papadakis

and Perakis (1990) treated the problem of minimal

time vessel routing in a region of deterministic wave

environment on the basis of the dynamic

programming approach. In this problem, the

navigation region is subdivided into several

subregions of different sea states. The optimal

navigation path is derived by determining the

sequence of subregions to be visited, which

minimizes the travelling time to a destination. Aside

432

Kim, K.

A Suboptimal Strategy for Autonomous Marine Vehicle Navigation in Variable Sea Currents.

DOI: 10.5220/0006906204320439

In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 2, pages 432-439

ISBN: 978-989-758-321-6

from the difficulty in establishing a practically

available numerical procedure adjoining the

formulation, the significant solution dependency on

the regional subdivision is a critical issue in the

approach. Some recent researches reported the

application of a generic algorithm (GA) to path

planning for an underwater vehicle in a variable

ocean. Major advantages of the GA over dynamic

programming are reduced computational complexity

and time, though it is susceptible to local minima,

however. Also, one of its significant drawbacks is a

strong constraint in generating the optimal path. In a

path planning application on the basis of GA, a user-

defined primary coordinate should strictly maintain a

monotonic increase in the optimal path (Alvarez et.

al, 2004). This is such a strong constraint that makes

it impossible to generate the optimal path containing

interim backward intervals.

Optimal guidance of a mobile vehicle in an arbitrarily

varied fluid environment is a strongly nonlinear

optimization problem, which is quite difficult to solve

numerically, as well as analytically. One of the recent

approach to treating this sort of problems is cell

mapping (Crespo and Sun, 2001). Though the cell

mapping is known to be especially adequate for

strongly nonlinear problems, computational demand

for obtaining a stable solution is enormous.

Path finding or guidance algorithms can be classified

into two categories according to the instant when its

solution is generated. While a pregenerative one

derives an unchangeable solution prior to a mission,

a reactive algorithm allows revised solution during

the mission (Alvarez et. al, 2004; Kamon and Rivlin,

1997). In this research, as a reactive strategy for

optimal vehicle navigation in varied sea current

environments, we propose a concept of suboptimal

navigation. In our problem of optimal navigation, the

minimum-time transit of a vehicle is attempted on the

basis of the optimal guidance law presented by

Bryson and Ho (1975). The solution of this guidance

law is a time sequence of the optimal headings. In an

actual field application for the minimum-time transit,

obtained optimal headings are tracked by a vehicle as

the reference in its heading control. Compact as it is,

the optimal guidance law is derived without

considering any specific dynamic constraint, like

many other path planning approaches. In our

suboptimal strategy, we compensate for this

drawback by incorporating reactive revisions in the

optimal navigation followed by tracking controls.

Once there happens a failure in tracking the optimal

trajectory due to the limitations in vehicle dynamics,

revised optimal navigation generates a new optimal

trajectory to be followed from then on.

In addition to the dynamic constraints, there are

several unfavorable environmental factors that might

be fatal in achieving the proposed optimal navigation.

Examples of such factors are uncertainties in sea

environments, severe sensor noises, or temporally-

faulty actuators (Burken et. al, 2001; Kim and Ura,

2009). As a fail-safe strategy, our suboptimal

navigation can cope with the failure in ongoing

optimal navigation due to any of the abovementioned

factors. The result of suboptimal navigation is not

rigorously optimal, but achieves a near-optimality

realized by the utmost in-situ actions as possible.

Though provides superior adaptiveness, robustness,

and more flexibility, a reactive approach in marine

vehicle navigation incurs a heavy computational cost

in its onboard implementation (Alvarez et. al, 2004;

Crespo and Sun, 2001; Kim and Ura, 2009). In this

research, we present a practical solution procedure of

highly reduced computational cost which derives the

numerical solution of the optimal guidance law in

implementing our suboptimal as well as optimal

navigation. This is a simple procedure applicable to

any sea current whether stationary or time-varying,

provided that its distribution at a specified instant is

deterministic. Robust global convergence is another

advantage of our procedure. On the basis of the

minimum principle (Bryson and Ho, 1975), it realizes

an efficient search space reduction, enabling optimal

solution search in a global manner. Due to this

algorithmic nature, our numerical procedure has a

much lower possibility of taking local minima,

compared to other search algorithms, primarily

relying on initial guesses.

As mentioned previously, deterministic sea current is

the prerequisite for implementing our optimal and

suboptimal navigation strategies. In many cases

however, it is not easy to obtain a predescribed

current distribution in the sea region of interest. One

of the simplest ways to build up sea current data is

direct measurement. Many governmental, public, or

private institutions related to maritime affairs provide

tabulated surface current distributions, obtained by

field measurements (McCormick, 2007; National

Ocean Service, 2002). The availability of these data

is more or less restrictive, because there are many sea

regions for which the current distribution data are not

built up or treated as confidential. As another source

of ocean environmental information, numerical

estimation models are playing an important role. By

assimilating the field measurement into them, some

recent numerical models provide both forecasts and

nowcasts of ocean fields with sufficiently accurate

mesoscale resolution (Robinson, 1999).

A Suboptimal Strategy for Autonomous Marine Vehicle Navigation in Variable Sea Currents

433

2 MINIMUM-TIME NAVIGATION

2.1 Problem Definition

As mentioned previously, the objective of the optimal

navigation presented in this study is the minimum-

time transit of a marine vehicle in sea currents. In still

water, a straight line connecting an initial position and

a destination is the shortest and thus the minimum-

time path. In regions of sea currents, however, smart

navigation possibly achieves the minimum-time

transit of a marine vehicle in which it takes the best

trajectory differing from the straight-line. In this

paper, we present a numerical solution procedure for

the minimum-time guidance law by Bryson and Ho

(1975). The solution of the guidance law is the

optimal heading reference, by tracking which a

vehicle achieves the minimum-time transit to the

destination, following the optimal trajectory.

In treating the minimum-time guidance law, we use

two sets of coordinate systems: the inertial (earth-

fixed) coordinate system o-xy and the body fixed

coordinate system o'-x'y', as shown in Fig. 1.

Figure 1: Coordinate systems for optimal guidance problem

formulation.

As the marine vehicle used in our navigation problem,

we employ an autonomous underwater vehicle

(AUV) "r2D4" described in Kim and Ura (2009). In

Figure 1, actuator inputs as well as kinematic

variables used in the lateral dynamic model of our

AUV are represented. While

denotes the main

thruster axis deflection,

and

are the deflections

of elevators on left and right sides, respectively.

Vehicle heading

is defined as the angular

displacement of the x'-axis relative to the x-axis. In

this work, we approximate that the direction of the

vehicle's advance velocity coincides with the x'-axis.

Since the distribution of a sea current is considered to

be deterministic in our research, current velocity is

described as a function of the position and time.

Therefore, on the assumption that the advance

velocity of a vehicle and the current velocity are

superimposable, the resultant vehicle velocity in a sea

current is expressed as

y,t)(x,vsinUyv

y,t)(x,ucosUxu

+==



(1)

where u and v are the components of the vehicle

velocity relative to the inertial frame, U

is the

advance speed of the vehicle in still water, and u

and

are the components of current velocity at a given

position and time. It is noted that we assume U

constant throughout a mission, which corresponds to

the operating condition of letting the rpm of vehicle's

main thruster fixed.

Equation (2) shows the minimum-time guidance law

of a marine vehicle moving in a sea current (Bryson

and Ho, 1975). Detailed procedure deriving (2) are

well explained in Kim and Ura (2009). It is noted here

that if only deterministic, there is no restriction on the

type of the sea current in (2). That is, not only

stationary, but also time-varying sea current can be

applied to (2) in deriving the solution for optimal

navigation. This leads to one of the most powerful

aspect of our approach over many other path planning

algorithms based on combinatorial optimization.

cos-sin2

sin

ccc

∂













∂

ψψψψ



(2)

2.2 Numerical Solution Procedure

Equation (2) is a nonlinear ordinary differential

equation (ODE) for an unspecified vehicle heading

(t). If the functions u

(x,y,t) and v

(x,y,t) describing

current velocity distribution are differentiable as well

as deterministic, the solution of (2) seems to be

attainable with an initial value of

(t), in terms of an

appropriate numerical solution algorithm such as

Runge-Kutta. However in practice, with an arbitrary

initial heading a vehicle travelling by the guidance

law (2) does not reach the destination. More precisely,

the initial value of vehicle heading is not arbitrary, but

is to be assigned correctly, consisting of a part of the

solution. This is because (2) is derived from the

Euler-Lagrange equation, which is a typical example

of the two-point boundary value problem,

characterized by split boundary conditions in states

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

434

and costates (Bryson and Ho, 1975). To obtain the

solution of a two-point boundary value problem, an

iterative solution procedure is usually required. The

most famous and commonly used numerical

procedures for such purpose are the shooting and the

relaxation methods (Press et. al, 1992). However,

direct applications of these methods to our minimum-

time navigation problem have significant difficulties.

In applying shooting method to a two-point boundary

problem in time domain, governing ODEs with

proper initial guesses should be integrated until

reaching the upper limit of the boundary. However,

as noticeable from its name, i.e., the minimum-time

navigation, our problem is a so-called free boundary

one, having unspecified upper limit in time domain.

In treating a free boundary problem by relaxation

method, on the other hand, the independent variable

should be transformed into a new one defined

between 0 and 1. Here, we can anticipate an intrinsic

serious difficulty in determining the stepsize in free

boundary problems. Properness of temporal grid

distribution ensuring convergence is initially

unknown and to know it is extremely difficult before

the end of a computation. Moreover, strong initial

guess dependency of the solution is another serious

concern in applying the relaxation method to our

problem, inappropriate selection of which possibly

leads to a local optimality or divergence (Press et. al,

1992).

As a new approach deriving the numerical solution of

the optimal guidance law (2), we presented a search

procedure which determines correct initial heading of

this two-point boundary value problem. Being named

AREN (Arbitrary Reference Navigation), our

procedure works globally on the basis of the

minimum principle. Figure 2 shows the algorithmic

scheme of our solution procedure. In Fig. 2, an

asterisked variable denotes the one corresponding to

the optimal solution. Refer to Kim and Ura (2009) for

the details of AREN. By applying the correct (i.e.,

optimal) initial heading

derived by AREN to (2)

and solving it in time domain, we can obtain the time

sequence of the optimal heading reference which

achieves the minimum-time transit to the destination.

It is noted here that the minimum distance l

min

shown

in Fig.2 is to be interpreted as the residual error in the

converged solution, since it represents how closely a

vehicle has approached the destination. Therefore,

when l

min

is unacceptably large, the optimal initial

heading should be refined by further searches

repeated in the vicinity of

Figure 2: Algorithmic scheme of the numerical solution

procedure AREN for deriving the optimal initial heading.

3 SUBOPTIMAL NAVIGATION

3.1 Optimal Navigation Validation

As a validation test of our solution procedure

explained thus far, we conducted a simulation of

minimum-time vehicle routing in a stationary flow

field. Deterministic as it is, the flow field is an

artificial one induced by multiple vortical sources. A

vortical source is a mathematical singularity made of

a point source superimposed by a point vortex. Once

its location and strength are determined, flow field

induced by a vortical source is immediately

calculated (Kim and Ura, 2009). Locations and

strengths of the vortical sources used in this example

are summarized in Table 1.

In this example, the AUV r2D4 is routed by three

different navigation strategies. The first one is so

called proportional navigation (PN), which might be

the simplest strategy for guiding a vehicle to a target.

Apply any navigation (e.g., Proportional Navigation) to a vehicle

routing simulation in maneuvering the vehicle to reach the destination.

Keep the travelling time obtained as t

f_ref

, the reference final time.

Applied navigation is called the "Reference Navigation"

Prepare N equispaced heading guesses

within 0 ~ 2

i= 0

Make a vehicle routing simulation following the minimum-

time guidance law (2). The simulation continues until t =

f_ref

starting with the initial heading

= 0. This simulation

is referred to as 0-th trial.

i= i+1

Assign current minimum distance and reference final time to

their optimal values, i.e., , .

(0)

min

ll =

(0)

f_ref

tt =

Find the minimum distance between the destination and the

vehicle trajectory generated by the 0-th trial. is the travelling time

in the 0-th trial corresponding to the vehicle position of .

(0)

min

(0)

f_ref

(0)

min

Make i-th trial vehicle routing simulation

with the initial heading .

N / i2

(i)

?ll

min

(i)

min

≤

i= N-1 ?

(i)

min

ll =

(i)

Accept as approximate optimal initial heading.

Yes

)( i

f_ref

tt =

A Suboptimal Strategy for Autonomous Marine Vehicle Navigation in Variable Sea Currents

435

In PN, the heading of a vehicle is continuously

adjusted to let its line of sight (LOS) direct toward the

target. It should be noted here that, by default, PN is

used as the reference navigation deriving the

reference final time t

f_ref

(Fig. 2), in our research. The

second one used for the performance exemplification

of our optimal navigation is straight-line tracking. As

noticeable from its name, the straight-line tracking

lets a vehicle follow a straight-line trajectory

connecting the initial position and the destination. In

a straight-line tracking, vehicle heading is determined

so as to compensate for the trajectory normal

component of the flow velocity at current vehicle

position. Detailed descriptions as well as at-sea field

results of the straight-line tracking navigation are

found in Kim and Ura (2002). In this paper, it is

assumed that the main thruster rpm of the AUV r2D4

is controlled to keep its water-reference velocity to be

1.54 m/s throughout any mission. In Fig. 3, vehicle

trajectories in the vortical source flow field obtained

by three different navigation strategies are shown.

Table 1: Locations and strengths of vortical sources.

No. Location (m)

Vortical source strength

Source strength

/s)

Vortex strength

/s)

1 -50 , 250 -15 -10

2 -100 , 400 -40 -30

3 -100 , 500 -50 -50

4 -250 , 600 40 -35

5 -200 , 150 30 30

6 -300 , 350 -35 -35

7 -400 , 550 30 30

8 120 , 540 -40 60

9 -500 , 0 -50 15

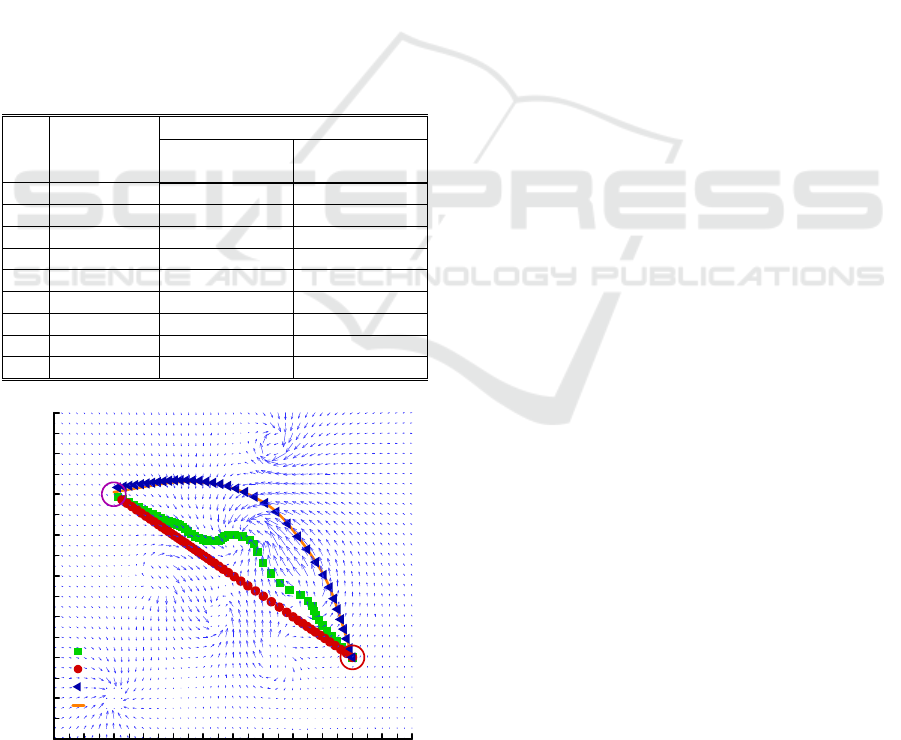
Figure 3: Vehicle trajectories in a vortical source flow.

In each navigation shown above, the vehicle moves

towards the destination at the origin, starting from the

initial position (-400 m, 800 m). Though it gets to the

final state at the destination, the vehicle following PN

experiences severe drift due to the interaction with

current flow. In the straight-line tracking, the vehicle

has difficulty in moving toward the destination,

because in a large portion its travel, it is made to

advance against the flow. In the optimal navigation

however, the vehicle takes a detouring trajectory

riding on favorable flows. The optimal navigation

enables the vehicle to get flow-induced speed

increase in favorable flows. Travelling time reduction

by this speed increase prevails over the extra

travelling time caused by the detour, resulting in the

travelling times of 795.0 s, 762.5 s, and 550.5 s,

corresponding to the PN, straight-line tracking, and

optimal navigation, respectively.

3.2 Suboptimal Strategy

The optimal navigation implemented by our solution

procedure seems to work properly and effectively, as

shown in the previous example. Here, it should be

noted that one of the essential prerequisites for

accomplishing the proposed optimal navigation is

that the system being treated is deterministic. Induced

by mathematical singularities, vortical source flows

are perfectly deterministic without any uncertainty. In

real world, however, any measurement data does

contain uncertainty. Another significant issue is the

dynamic constraint. An optimal trajectory obtained

by solving the guidance law (2) is the one derived

without considering dynamic constraints of a specific

vehicle. This means that some optimal trajectories are

not able to be realized unless a vehicle exerts

unrealistic velocity or acceleration. As a remedy for

such issues, we propose the strategy of suboptimal

navigation. The suboptimal navigation is a fail-safe

strategy towards the field implementation of the

optimal navigation. The basic idea of the suboptimal

navigation presented in this paper is rather simple. Let

denote the deviation distance between the present

vehicle position and the preassigned one on the

optimal reference trajectory. When d

exceeds a

prescribed acceptable limit set for preserving an

ongoing optimal navigation, the high-level controller

for the vehicle navigation is activated and revises the

current optimal trajectory. By re-applying the AREN

to current vehicle position, velocity, attitude, as well

as environmental conditions, optimal trajectory as the

reference is newly revised. Figure 4 depicts the

schematic of the suboptimal navigation explained

thus far.

Lateral Posi tio n (m)

Longi t udinal Position (m)

-200 -100 0 100 200 300 400 500 600 700 800 900 1000

-600

-500

-400

-300

-200

-100

100

200

: Optimal Reference

: Propor t i opnal Navigation

: Straight-line Tracking

:Optimal(Tracked)

Initial Position

Destination

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

436

Figure 4: Schematic of the suboptimal navigation.

4 APPLICATIONS

4.1 Suboptimal Navigation in

Northwestern Pacific

In what follows, we apply the suboptimal navigation

to actual sea environments. The sea region selected

for the first example is located in the Northwestern

Pacific Ocean near Japan. The daily updated sea

current data of this region is available at https://www.

data.jma.go.jp/kaiyou/data/db/kaikyo/daily/current_

HQ.html?areano=2 presented by the Japan

Meteorological Agency. The most notable

environmental characteristic in this sea region is the

current field dominated by the Kuroshio. The

Kuroshio is a strong western boundary current

flowing northeastward along the coast of Japan.

At first, the optimal navigation has been applied to the

vehicle routing in the abovementioned sea region. In

this example, we do not consider any environmental

uncertainty in the sea current data. Figure 5 shows the

vehicle trajectories obtained by three different

navigation strategies: PN, straight-line tracking, and

optimal navigation.

Figure 5: Vehicle trajectories in a Northwestern Pacific

Ocean region.

As shown in the figure, like the preceding example in

which exact values of current velocity and its

gradients are available anywhere in the region, the

vehicle tracks the optimal reference trajectory with a

negligibly small deviation. This indicates that our

strategy of optimal navigation is also valid in the

actual sea current data.

In the following example, we apply the optimal

navigation to a vehicle routing in the same sea region

that was used in the preceding example. The only

thing different from the preceding example is we

consider uncertainty in our sea current data in order

to enhance the reality of our optimal navigation. An

environmental uncertainty model is introduced in

determining sea current velocities. The uncertainty

components in the sea currents are expressed as

additive white Gaussian noise (AWGN). Taking the

sea current velocities in the Northwestern Pacific

Ocean used beforehand as the mean values, on-site

current velocities including uncertainty are given by

(x,y,t) = u

(x,y,t) + e

(

)

(x,y,t) = v

(x,y,t) + e

(

)

(3)

where u

and v

are the components of the on-site

current velocity, u

and v

are the components of the

deterministic current velocity taken from the database,

and e

(

) and e

(

) are the AWGNs with standard

deviation

. As the parameter for specifying the value

in a given navigation region, we introduce the

regional mean current speed U

defined as



(4)

where i denotes the index covering all grid nodes on

which the database-based current velocities are

defined. In Fig. 6, vehicle trajectories obtained by

optimal navigation applied to different levels of

velocity uncertainties are shown. When the level of

velocity uncertainty is such that

= 2U

, the optimal

trajectory derived without considering uncertainty

still seems to work acceptably. As a result, though

slightly deviating from the destination, the final

position of the vehicle remains in the vicinity of the

destination. When the level of velocity uncertainty

increases up to

= 4U

, however, following the

optimal trajectory can no longer make the vehicle

approach the destination, as shown. As was

demonstrated in this example, the optimal navigation

proposed in this research bears the risk of failure

which increases in proportion to the degree of

environmental uncertainty.

Tokyo

Kii

Peninsula

Mainstream of Kuroshio

Initial Position

(Minamiizu)

Boso

Peninsula

Izu Peninsula

: Straight-line Tracking

Destination

: Optimal Reference

: Propor t i onal Navigation

: Optimal (Tracked)

Pacific Ocean

A Suboptimal Strategy for Autonomous Marine Vehicle Navigation in Variable Sea Currents

437

Figure 6: Vehicle trajectories in a Northwestern Pacific

Ocean region. In this example, on-site sea current velocities

are generated to include uncertainties expressed by

AWGNs.

Next, we apply the suboptimal navigation to a vehicle

routing in the same sea region. In the suboptimal

navigation, however, the vehicle does not merely

track the pregenerated optimal reference trajectory

throughout, but regenerates and follows new ones

whenever necessary, adapting to the current states of

environment as well as the vehicle position. Figure 7

shows the result of suboptimal navigation.

Figure 7: Vehicle trajectories by suboptimal navigation.

In Fig.7, it is noted that during the travel the optimal

navigation has been revised five times. Discontinuous

intervals appearing in the optimal reference trajectory

indicate the occurrences of the optimal navigation

revisions. These revisions enable the vehicle to arrive

at the destination.

Figure 8: Monitored vehicle trajectories by suboptimal

navigation in a tidal flow in Tokyo Bay observed at (a)

12000.0 s (b) 18000.0 s (c) 24251.0 s.

Tokyo

Kii

Peninsula

Pacific Ocean

Initial Position

(Minamiizu)

Boso

Peninsula

Izu Peninsula

:Optimal( )

Destination

: Optimal (without Uncertainty)

:Optimal( )

σ U

=2U

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

438

4.2 Suboptimal Navigation in a

Time-Varying Sea Current

The last optimal navigation example presented in this

paper is an underwater vehicle routing in Tokyo Bay.

In this example, we consider the mission of

minimum-time homing to the port of Yokohama. Due

to its narrow entrance and shallow depth, sea currents

in Tokyo Bay are hardly affected by the outer ocean

currents such as Kuroshio. Instead, like many other

littoral zones, currents in Tokyo Bay are dominated

by the tidal flow. In this research, we use the time-

varying sea current distribution data in Tokyo Bay,

generated by a numerical tidal flow simulation model

by Kitazawa et al. (2001). Figures 8(a) ~ (c) are

sequential vehicle trajectories derived by applying the

suboptimal navigation. By the suboptimal navigation

consisting of total four self-revisions, the vehicle has

accomplished its homing mission.

5 CONCLUSIONS

In this paper, a systematic procedure for obtaining the

numerical solution of the optimal guidance law for a

marine vehicle moving in a region of sea current has

been presented. Reduced computational cost is one of

the outstanding features of our solution procedure.

Whilst linearly proportional to the area of a search

region in dynamic programming, the computational

time in our procedure exhibits square root

dependence on it. Moreover, unlike other path finding

algorithms such as dynamic programming or generic

algorithm, our procedure does not extend search

space when applied to a time-varying problem. This

means a great advantage that a time-varying problem

can be solved merely using the same computational

cost as is required for solving a time-invariant one.

As a fail-safe strategy for the field application of the

optimal navigation, suboptimal navigation has been

proposed. The fact that there actually are several

uncertainties which possibly disrupt ongoing optimal

navigation emphasizes the practical importance of the

suboptimal strategy proposed by us.

ACKNOWLEDGEMENTS

The author would like to thank Prof. D. Kitazawa of

IIS, the University of Tokyo for providing simulated

tidal flow data of Tokyo Bay.

REFERENCES

Nicholson, J. W., Healey, A. J., 2008. The present state of

autonomous underwater vehicle applications and

technologies. Marine Technology Society Journal,

42(1), 44-51.

Kim, K., Ura, T., 2010. Applied model-based analysis and

synthesis for the dynamics, guidance, and control of an

autonomous undersea vehicle. Mathematical Problems

in Engineering, 2010, Article ID 149385, 23 pages.

doi:10.1155/2010/149385.

Crespo L. G., Sun, J. Q., 2001. Optimal control of target

tracking with state constraints via cell mapping. J. of

Guidance, Control, and Dynamics, 24(5), 1029-1031.

Zhao, Y., Bryson, A. E., 1990. Optimal paths through

downbursts. J. of Guidance, Control, and Dynamics,

13(5), 813-818.

Alvarez, A., Caiti, A., Onken, R., 2004. Evolutionary path

planning for autonomous underwater vehicles in a

variable ocean. IEEE J. of Oceanic Engineering, 29(2),

418-429.

Papadakis, N. A., Perakis A. N., 1990. Deterministic

minimal time vessel routing. Operations Research,

38(3), 426-438.

Kamon, I., Rivlin, E., 1997. Sensory-based motion planning

with global proofs. IEEE Trans. on Robotics and

Automation, 13(6), 814-822.

Kim, K., Ura, T., 2009. Optimal guidance for AUV

navigation within undersea area of current disturbances.

Advanced Robotics, 23(5), 601-628.

Bryson, A. E., Ho, Y. C., 1975. Applied Optimal Control,

Taylor & Francis, Levittown.

Burken, J. J. et al., 2001. Two reconfigurable flight-control

design methods: Robust servomechanism and control

allocation. J. of Guidance, Control, and Dynamics,

24(3), 482-493.

McCormick, H., 2007. Reed's Nautical Almanac: North

American West Coast 2008, Thomas Reed Publications.

National Ocean Service, 2002. Tidal Current Tables 2003,

Pacific Coast of North America and Asia, International

Marine Publishing.

Robinson, A. R., 1999. Forecasting and simulating coastal

ocean processes and variabilities with the Harvard

Ocean Prediction System. In: Mooers, C.N.K. (eds.)

Coastal Ocean Prediction, 77-100.

Press, W. H., Flannery, B. P., Teukolsky, S. A., Vetterling,

W. T., 1992. Numerical Recipes in Fortran, Cambridge

University Press.

Kim, K., Ura, T., 2002. 3-dimensional trajectory tracking

control of an AUV "R-One Robot" considering current

interaction. In Proceedings of Int. Offshore and Polar

Engineering Conf., 277-283, Kita-Kyushu.

Kitazawa, D. et al., 2001. Predictions of coastal ecosystem

in Tokyo Bay by pelagic-benthic coupled model. In

Proceedings of 20th Int. Conf. on Offshore Mechanics

and Arctic Engineering, Rio de Janeiro, OSU-5035.

A Suboptimal Strategy for Autonomous Marine Vehicle Navigation in Variable Sea Currents

439