Multicasting in Tactical Networks: Forwarding Versus Network Coding

Ola Ashour, Marc St-Hilaire and Thomas Kunz

Systems and Computer Engineering, Carleton University, Ottawa, Canada

Keywords:

Multicast, Network Coding, Packet Forwarding, Lower Bounds, Tactical Networks.

Abstract:

Multicasting refers to the transmission of packets to a group of one or more destinations. It can be very useful

in military applications, such as command and control, in which a commander needs to send instructions to a

group of tanks, users, or planes. Broadcast is a unique case of multicast, where all the nodes in the network

are intended receivers. The broadcast case has been studied quite extensively in the literature, showing that the

use of Network Coding (NC) requires fewer data transmissions than Packet Forwarding (PF). That motivates

us to explore whether the same result holds true when only a subset of nodes are receivers. In this paper,

we developed two linear optimization models that determine lower bounds on the number of required data

packet transmissions when sending data in a Mobile Ad-hoc Network (MANET) from a single source to

multiple receivers. The ﬁrst model determines the minimum number of required packet transmissions under

the assumption that PF is used. The second model assumes that data is distributed using NC. We derive lower

bounds for different scenarios while varying the network size, network density, and the number of receivers in

the multicast group and compare them with each other. Results indicate that the lower bounds for both PF and

NC are almost the same for smaller network sizes (30 nodes or less), small multicast group sizes (5 or lower),

or dense networks. However, for larger network sizes, sparser networks, and larger multicast group sizes NC

is more advantageous than PF.

1 INTRODUCTION

Tactical networks are MANETs that are temporarily

formed using radios with relatively long range and

very limited bandwidth. These networks are built

from mobile nodes such as sensors, soldiers and ve-

hicles that communicate through tactical radio links.

Most of the communications over tactical networks

are group-oriented, requiring the transmission of the

same data to several destinations. One example would

be transmitting instructions from military headquar-

ters to a group of military units that are moving to-

gether such as a squad, platoons, or battalions (Refaei

and Bush, 2014; Egbogah et al., 2008). In such an en-

vironment, using unicast transmission is not efﬁcient,

so multicasting can be a good solution.

Multicasting refers to the transmission of packets

to a group of nodes identiﬁed by a single multicast

group address. Several multicast routing protocols

have been proposed to address the problem of data

distribution in MANETs which require transmitting

data from single or multiple sources to multiple desti-

nations.(Royer and Perkins, 1999; Lee et al., 2002;

Lucile Canourgues and Beylot, 2006). These mul-

ticast routing protocols assume that packets are for-

warded on a per-packet basis as would be the case in

the Internet. Ahlswede et al. (Ahlswede et al., 2000)

introduced a new idea to enhance the multicast trafﬁc

throughput called Network Coding (NC). NC enables

the nodes to combine or encode a certain number of

incoming packets together instead of simply forward-

ing them. One of the popular coding schemes is called

Random Linear Network Coding (RLNC). RLNC al-

lows a node to linearly combine a number of pack-

ets into one or more coded packets. A coding vector

that contains the coding coefﬁcient of the constituent

packets is then appended to each coded packet. The

receiving node must receive a certain number of lin-

early independent coded packets (at least equal to the

number of original packets) to be able to decode the

received packets.

In this paper, we are interested in comparing the

lower bounds obtained from applying PF and NC

to a multicast scenario. Our key metric is the re-

quired number of data packet transmissions at the

MAC layer. Unlike most of the previous work, which

explored the use of NC for increasing the multicast

throughput, we are interested in exploring ways to

distribute a given amount of data most efﬁciently to

Ashour, O., St-Hilaire, M. and Kunz, T.

Multicasting in Tactical Networks: Forwarding Versus Network Coding.

DOI: 10.5220/0006907900420051

In Proceedings of the 15th International Joint Conference on e-Business and Telecommunications (ICETE 2018) - Volume 1: DCNET, ICE-B, OPTICS, SIGMAP and WINSYS, pages 42-51

ISBN: 978-989-758-319-3

a group of receivers. The fewer packet transmissions

a given approach requires, the fewer radio resources

and (ﬁnite) battery energy are required. To that end,

we develop two linear optimization models that, given

a network scenario, determine lower bounds on the

required number of data packet transmissions when

sending data in a MANET from a single source to

multiple destinations. Both linear programs are opti-

mistic in that they assume that packets are never lost,

in addition to being forwarded over the optimal path.

The outline of this paper is as follows. Section 2

reviews related work. Section 3, describes the PF and

NC linear programs and compare the results obtained

from both models. Finally, conclusions and future

work are provided in Section 4.

2 RELATED WORK

There exist several work that addressed the problem

of data distribution in MANETS. Some methods ap-

plied multicast routing protocols which is based on PF

to enhance bandwidth utilization. Gopinath and Na-

garajan (Gopinath and Nagarajan, 2015) proposed the

residual energy-based reliable multicast routing pro-

tocol (RERMR), which increases packet delivery ra-

tio and network life time. This is achieved by inte-

grating a stability model with a multicast backbone

to improve node stability and link quality. The pro-

tocol estimates the reliability of each path, as well as

the residual energy of its nodes. The path with higher

reliability and residual energy is then chosen for for-

warding data packets. The algorithm monitors the er-

ror rate on each path and if the error rate for a certain

path increases, another path will be selected. Sim-

ulation results show that the proposed algorithm has

better performance in terms of higher delivery ratio,

network stability, and lower delay. However, the algo-

rithm assumes a priori knowledge of nodes direction

of motion.

The problem of ﬁnding the minimal set of for-

warding nodes for broadcasting in the PF case

is called the Minimum Connected Dominating Set

(MCDS) problem and is known to be NP-hard (

Cagalj

et al., 2002). The best exact solution to ﬁnd a Mini-

mum Connected Dominating Set of an arbitrary graph

of n nodes is described in (Fomin et al., 2008) and

solves the problem in O(1.9407

), a slight improve-

ment of the trivial (2

) algorithm. If the complete

topology is known, centralized heuristics such as the

one in (Butenko et al., 2004) can be applied and pro-

vide in general a good approximation to the MCDS

size. The work done in (Kunz et al., 2010) imple-

mented this heuristic to derive the lower bound for

broadcasting data from one source to all nodes in the

network based on PF.

Other methods suggest the use of NC to reduce

duplicate packet transmission and enhance the trans-

mission efﬁciency of the network.The work done by

Lun et al. (Lun et al., 2008), propose the use of Ran-

dom Linear Network Coding (RLNC) to provide reli-

able communication in lossy multi-hop wireless net-

works. RLNC enables the node to linearly combine a

number of incoming packets to produce a single en-

coded packet that conveys useful information about

the whole data set. The encoded packets are then

transmitted over the wireless channel in which pack-

ets can get lost. However, if the receiving node re-

ceives a certain number of linearly independent coded

packets, it can reconstruct the original message. This

ensures a reliable delivery of data.

Determining the lower bounds in the case of net-

work coding was formulated as a linear optimization

problem in (Kunz et al., 2010; Kunz et al., 2012).

The program minimizes the total number of packet

transmissions by all nodes, subject to the constraints

that each receiver has to receive M coded data packets

from each source. The underlying assumption is that,

if a source generates M coded data packets, a receiver,

upon receipt of all M coded data packets, will be able

to decode them and regenerate the original data pack-

ets. A RLNC broadcast protocol called ARLNCCF

was proposed in (Kunz et al., 2012). The protocol

supports the use of cross source coding by allowing

packets from different sources to be coded together.

Results showed that the use of cross source coding

can decrease the number of packet transmitted in the

network by 8%-20%. Moreover,the PDR was im-

proved and packet latency was decreased. However,

the protocol complexity increased due to the need for

managing packets from different sources.

Broadcast is a unique case of multicast, where

all the nodes in the network are intended destina-

tions. (Fragouli et al., 2008) studied in-depth the case

for all-node broadcasting (all sources generate a data

packet that then has to be shared with all other nodes

in a wireless multi-hop network). The paper shows

that for certain regular topologies (ring, square grid),

NC can distribute the data at a competitive advan-

tage over PF, which they refer to as coding gain. In

the case of a ring topology, as the number of nodes

grows, NC requires only half the number of packet

transmissions compared to PF. In the grid topology,

PF requires about 33% more packet transmissions.

More generally, the theoretical analysis in the paper

shows that network coding improves performance by

a constant factor in ﬁxed networks. In networks where

the topology dynamically changes, for example due to

Multicasting in Tactical Networks: Forwarding Versus Network Coding

mobility, and where operations are restricted to sim-

ple distributed algorithms, network coding can offer

improvements of a factor of log n, where n is the num-

ber of nodes in the network.

3 OPTIMIZATION MODELS

The previous section showed that NC can have signif-

icant performance beneﬁts over PF in various broad-

casting scenarios, in particular as the network size

increases. On the other hand, in the case of a sin-

gle source and a single destination (unicasting), there

is no difference between PF and NC: the minimum

number of packet transmissions at the MAC layer

is achieved by forwarding all data or coded packets

over the shortest hop path connecting source and des-

tination. In this section, we want to examine cases

between these two extremes. Is NC beneﬁcial in

scenarios where a single source multicasts data to a

(relatively small) number of receivers? To answer

this question, we developed two linear optimization

models using IBM ILOG CPLEX Optimization Stu-

dio. The programs determine lower bounds on the

required number of data packet transmissions when

sending data in a MANET from a single source to

multiple destinations.

3.1 Problem Formulation

Consider a static wireless ad-hoc network with N

nodes, that are randomly positioned in a square area,

based on a uniform distribution. To compare the

lower bounds in a meaningful way, we generated 25

network scenarios with the setdest utility in NS2,

which places a certain number of nodes within a given

area, using a uniform random distribution. We vary

both the number of nodes in the network as well as the

network density. We created networks with 10 to 100

nodes in steps of 10. The network size scales with the

number of nodes to keep the nodal density approx-

imately constant. To explore the impact of network

density, three sets of network scenarios were created,

which we refer to as Sparse Density, Medium Den-

sity, and High Density. In Sparse Density, the net-

work area ranges from 470 m x 470 m for a 10 node

network to an area of size 1500 m x 1500 m for a 100

node network. With an assumed transmission range

of 250 m, nodes have, on average, slightly below 2

neighbors. All networks are connected. In Medium

Density networks, the area size ranges from 346 m

x 346 m to 1095 m x 1095 m, with nodes having, on

average, slightly more than 4 neighbors. In High Den-

sity networks, the area size ranges from 255 m x 255

m to 806 m x 806 m, nodes have, on average, 8 to 9

neighbors.

In all scenarios, we assume that we have a single

source which is node zero that needs to transmit data

to a number of destinations (d). The number of re-

ceivers in the multicast group can vary from 2 to 5

and 9 which is the maximum number of destinations

that can exist in a 10 nodes network (the smallest net-

work size we consider). The linear programs assume

that the nodes with the highest ID are multicast re-

ceivers. As an example, if the user speciﬁes that d

nodes (out of N) are to be receivers, the model uses

nodes N-d to N-1 as the receiving nodes. With ran-

dom node placements, these receivers could be close

or far away from the source node (always node 0).

The number of packet transmissions will be very sen-

sitive to the relative location of source and destina-

tions, particularly for smaller multicast group sizes

and sparser networks. To allow for coding opportu-

nities, the source node has to send more than a sin-

gle data packet, so the two linear programs assume

that the source sends 1000 data packets. We will use

these scenarios to evaluate/compare PF and NC lower

bounds.

Table 1 summarizes all experimental parameters

we varied in this paper.

Table 1: Experimental Parameters.

Parameter Possible Values

Number of Nodes 10, 20, 30, 40, 50, 60, 70,

80, 90, 100

Network Density Sparse, Medium, High

Multicast Group Size 2, 5, 9

3.2 Packet Forwarding Model

The lower bound for PF is derived using a linear pro-

gram which is illustrated as follow. Let s represent

the source node, P represent the number of packets

transmitted by the source node, N(i) is the set of one

hop neighbours of node i, X

is the number of pack-

ets transmitted by node i, F

i, j

(d) is the data ﬂow from

source node s over link (i,j) to destination d. The ob-

jective of the optimization model is to minimize the

total number of packets transmitted by all the nodes

in the network.

min

∑

Subject to:

Constraint 1: the ﬂow over any link (i,j) to desti-

nation d should be greater than or equal to zero.

i, j

(d) >= 0 (i, j ∈ N) (1)

DCNET 2018 - International Conference on Data Communication Networking

Constraint 2: ﬂow balance constraints which indicates

that, if i is the source node, it has to transmit P pack-

ets. If i is the destination node, it has to receive P

packets. For any other intermediate node, the sum

of outgoing ﬂows minus the sum of incoming ﬂows

should be zero.

∑

j∈N(i)

i, j

(d) −

∑

l∈N(i)

l,i

(d) =











P f or i = s

−P f or i = d

0 otherwise

(2)

Constraint 3: the ﬂow over existing link (i,j)

should not exceed the number of packets transmitted

by the head of the link.

≥ F

i, j

(d) (i, j ∈ N) (3)

Constraint 4: the ﬂow over any link is either all

the packets or none.

i, j

(d) = P || F

i, j

(d) = 0 (i, j ∈ N) (4)

Figures 1 to 3 plot the lower bounds when using

PF to implement multicasting for various multicast

group sizes. The X axis plots the number of nodes in

the network, the Y axis shows the number of packet

transmissions to send a single packet to all destina-

tions in the multicast group, averaged over all 25 sce-

narios. The results presented also include the 95%

conﬁdence interval.

The results illustrate that we need more packet

transmissions per data packet for larger networks, as-

suming the network density remains constant. We

also require more packet transmissions as the multi-

cast group size increases. Finally, as network density

increases, fewer packet transmissions are necessary to

reach all multicast group members.

3.3 Network Coding Model

Determining the lower bounds in the case of NC is de-

rived using the linear program we introduced in (Kunz

et al., 2010), but here we are interested in multicast

scenarios where only a subset of the nodes are inten-

dent destinations. The main difference between the

PF and NC linear programs is in Constraint 4 which

indicates that the ﬂow over any link is either all the

packets or none. This constraint can not be used in

the case of NC as it will force the node to forward

all the packets it received and the idea of NC is to al-

low the node to combine multiple incoming packets

into one or more outgoing coded packets. Removing

that constraint will raise another problem which will

be illustrated using the following example. Consider

a ring network consisting of six nodes, and assume

that the source node (node 1) wants to transmit two

packets (a and b) to destination nodes 3, 4, and 5. If

we use PF, the minimum number of required packet

transmission to deliver the two packets to all the three

destinations is 8 packets as shown in Figure 4. Node

1 will transmit the two packets to its one hop neigh-

bours node 2 and 6, then node 2 will transmit the two

packets to node 3. Meanwhile node 6 will transmit

the two packets to node 5. Finally either node 3 or

node 5 will transmit the two packets to node 4. How-

ever, if we remove Constraint 4, the result from the

optimization program indicate that we need only 6

packet transmissions to deliver the two packets to all

the destinations. Figure 5 illustrates how packets are

transmitted in the case of NC. The source node will

transmit packet a to node 2 and packet b to node 6,

node 2 will transmit packet a to node 3, while node

6 will transmit packet b to node 5. After that node 3

will transmit packet a to node 4. Meanwhile node 5

will transmit packet b to node 4. In this case, node

4 received the two packets a and b, but each of node

3 and 5 received only one packet, so node 4 will en-

code packet a and packet b and transmit one encoded

packet (a ⊕ b) which will be received by nodes 3 and

5. Nodes 3 and 5 will decode the received encoded

packet to obtain the missing packet (either a or b). The

problem that arises here is that although the source

node transmitted two packets when it sent packets a

and b, and each transmission occupies the transmis-

sion media, the minimum number of packet transmis-

sion should be 7 not 6. However, if we account for

physical packet transmissons the way we do in the PF

case, these two transmissons would only be counted

as one packet transmission sent by the source node.

In order to ﬁx this problem we introduce the notion of

dummy nodes. In the above scenario, the two pack-

ets transmitted by node 1 will ﬁrst be sent to node 1’s

dummy node, and count as two physical packet trans-

missions, before the dummy node forwards the two

packets to different intended receivers.

We assume that any real node i has to transmit the

packets to its dummy node

i, which in turn will for-

ward the packets to the direct neighbours of i. Assume

that we are again transmitting P packets, which now

may be coded (i.e., combinations of native data pack-

ets). The objective of the program is to minimize the

total number of packets transmitted by all nodes in the

network.

min

∑

Subject to:

Const. 1: the ﬂow from node i to its dummy node

should be less than or equal to the number of physical

packets transmitted by that node.

>= F

(d) ∀ i, j ∈ N (5)

Multicasting in Tactical Networks: Forwarding Versus Network Coding

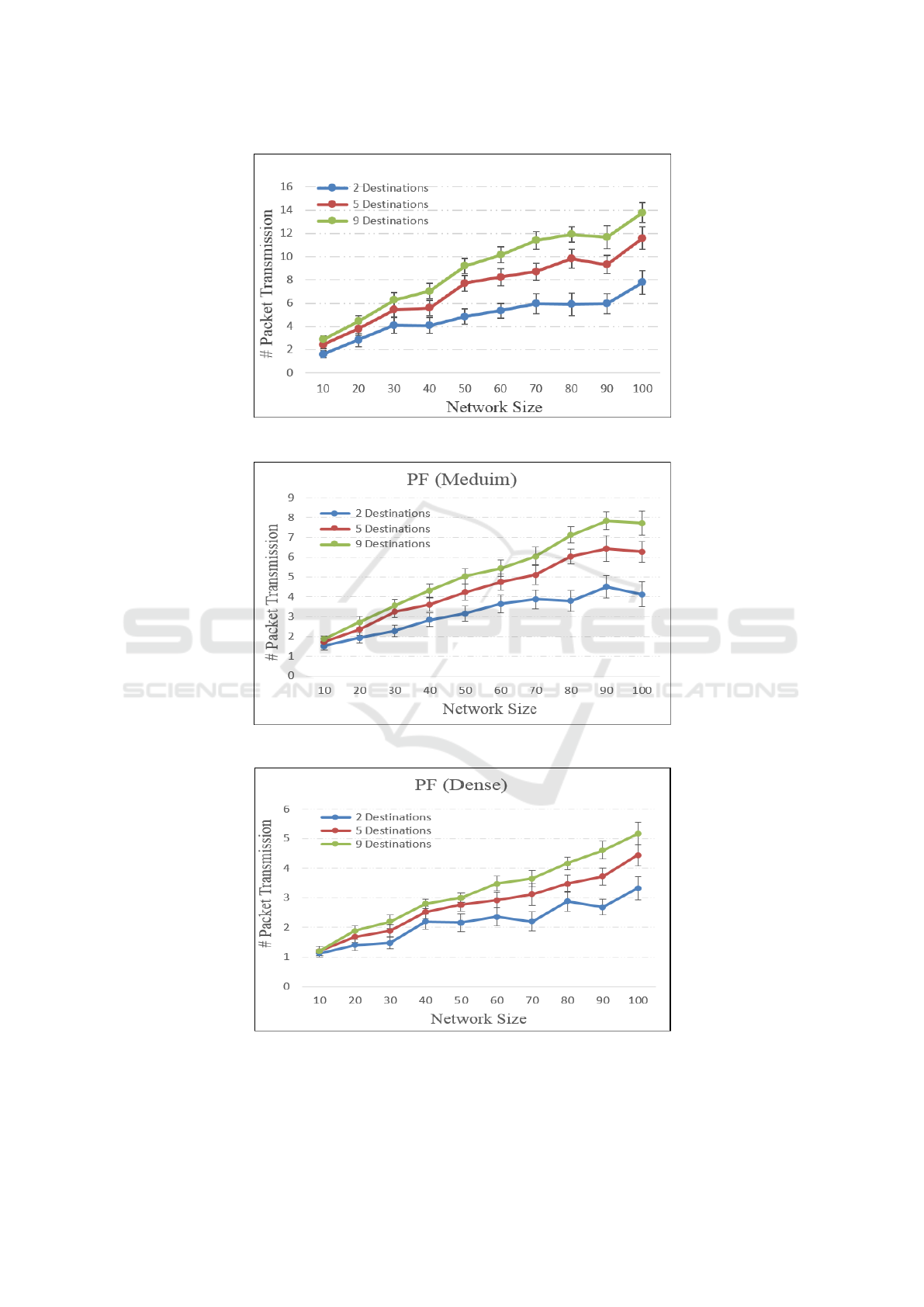
Figure 1: Lower Bounds for PF in Networks of Sparse Density.

Figure 2: Lower Bounds for PF in Networks of Medium Density.

Figure 3: Lower Bounds for PF in Networks of High Density.

Const. 2: ﬂow balance constraints which indicate that

the source node has to generate P packets and the

destination node should receive P coded data pack-

ets. Otherwise, the node should forward all the data

DCNET 2018 - International Conference on Data Communication Networking

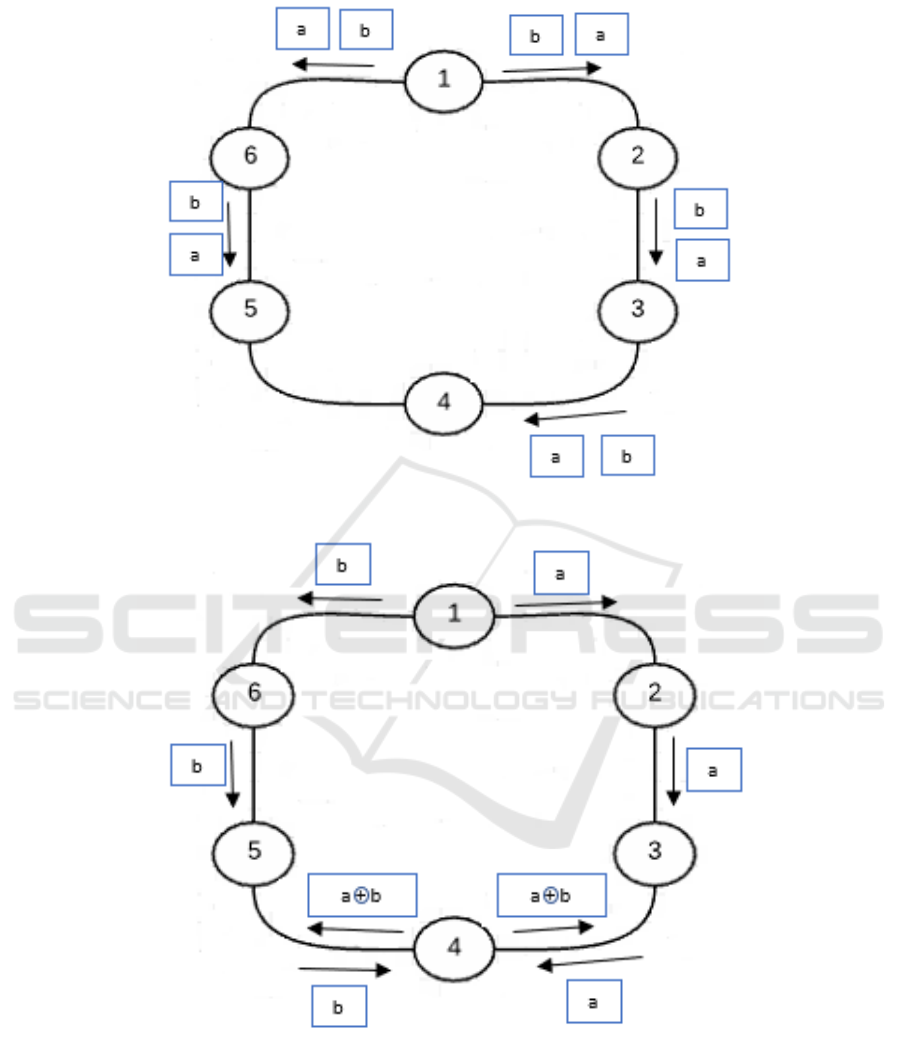
Figure 4: Packet Transmission using PF.

Figure 5: Packet Transmission using NC.

packets it received to its dummy node.

(d) −

∑

j∈N(i)

j,i

(d) =











P f or i = s

−P f or i = d

0 otherwise

(6)

Const. 3: the ﬂow balance constraints on the

dummy node is zero.

∑

j∈N(i)

i, j

(d) − F

(d) = 0 (7)

Const. 4: the number of packets transmitted by

any node i should be greater than or equal to zero.

>= 0 ∀ i ∈ N (8)

Multicasting in Tactical Networks: Forwarding Versus Network Coding

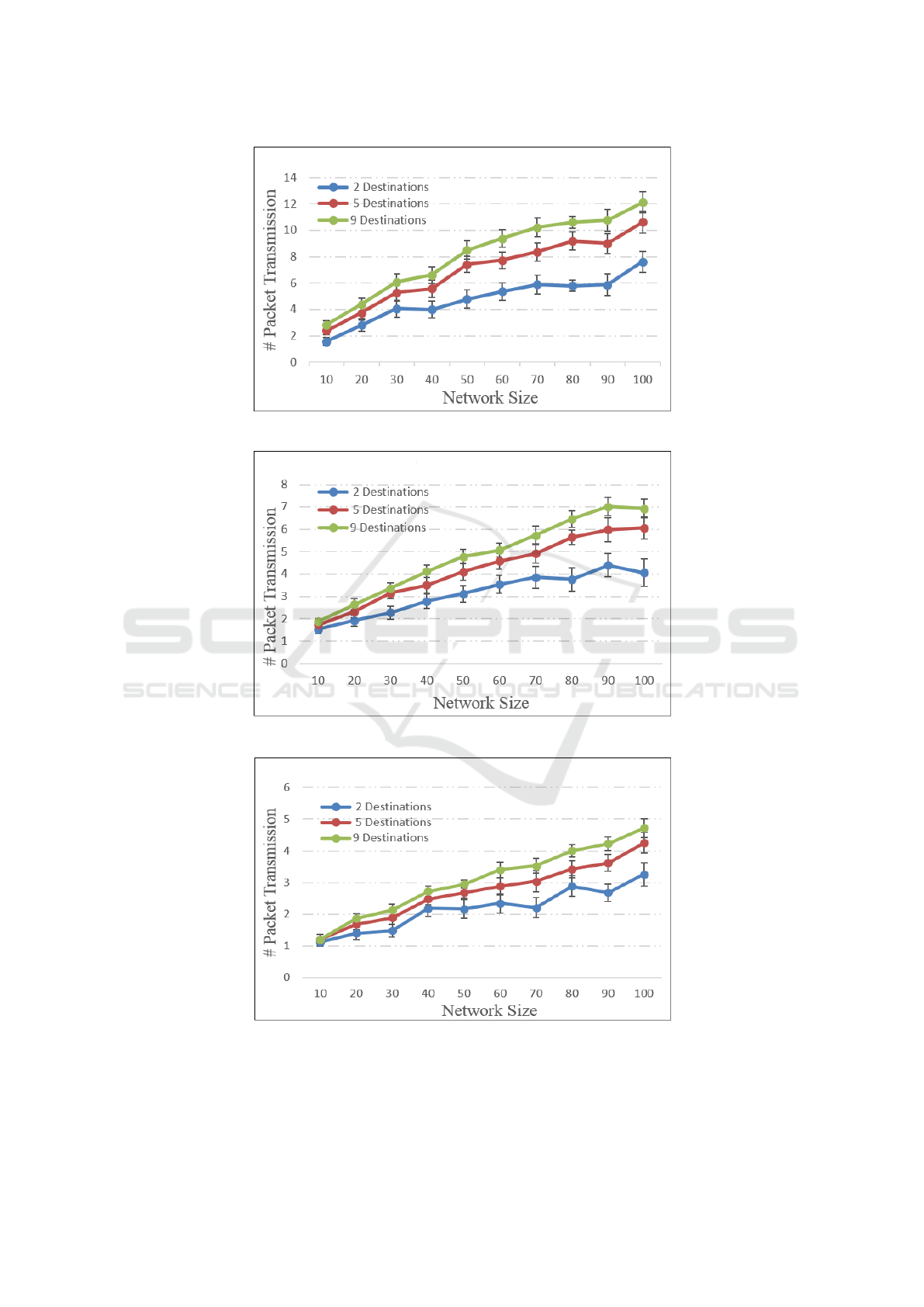
Figure 6: Lower Bounds for NC in Networks of Sparse Density.

Figure 7: Lower Bounds for NC in Networks of Medium Density.

Figure 8: Lower Bounds for NC in Networks of High Density.

Figures 4 to 6 plot the lower bounds when us-

ing NC to implement multicasting for various multi-

cast group sizes. The 95% conﬁdence intervals are

quite tight, giving us assurance that the results av-

eraged over 25 scenarios are meaningful enough to

draw some conclusions/observations from our data.

DCNET 2018 - International Conference on Data Communication Networking

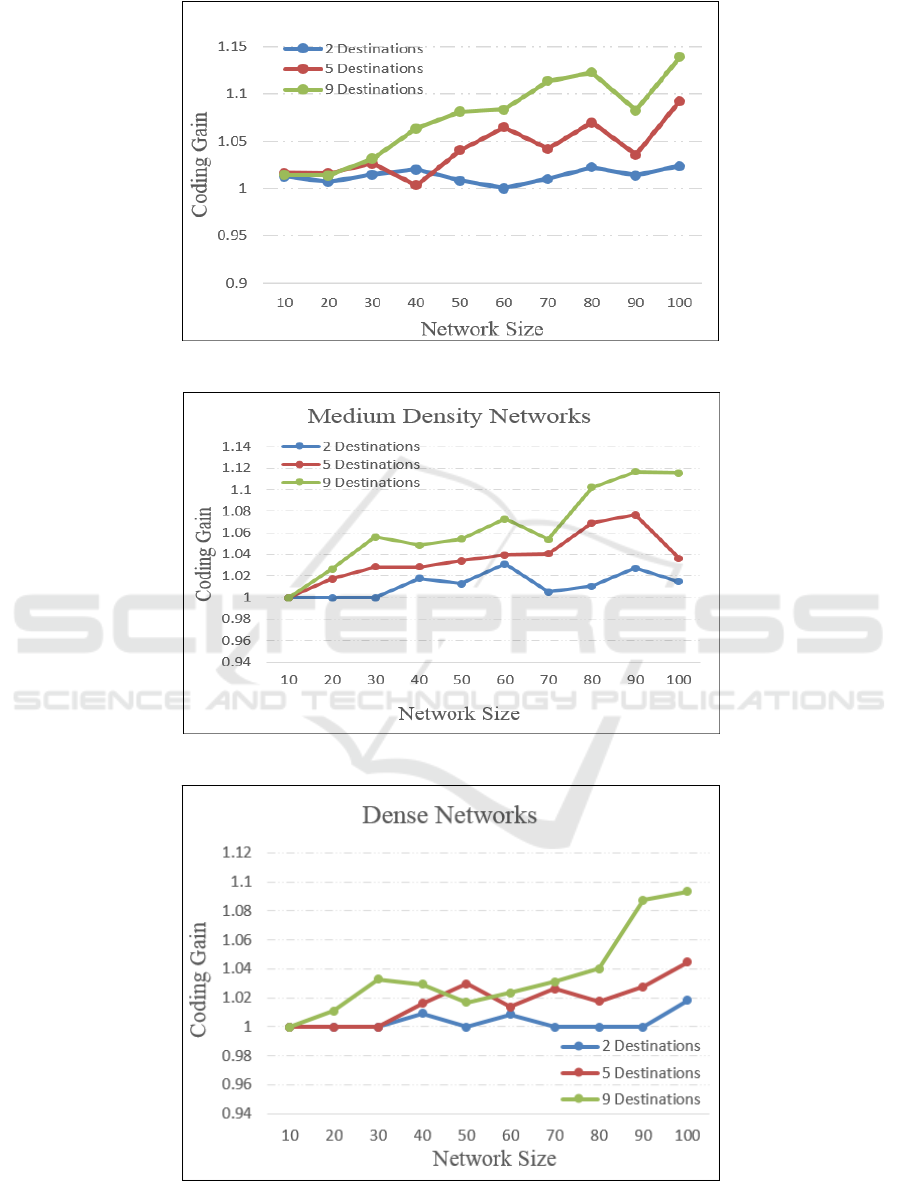
Figure 9: Coding Gain in Networks of Sparse Density.

Figure 10: Coding Gain in Networks of Medium Density.

Figure 11: Coding Gain in Networks of High Density.

Multicasting in Tactical Networks: Forwarding Versus Network Coding

Similar to the PF results, NC results show that

as the multicast group size increases, more packet

transmissions are required to reach all group mem-

bers. For a given network density, as the number of

nodes increases, again more packet transmissions are

required, as destinations are (potentially) further away

from the multicast source. Finally, as network density

increases, the network diameter shrinks, resulting in

fewer packet transmissions to reach a given number

of multicast receivers.

3.4 Comparing NC and PF Results

Based on the results obtained from PF and NC in the

previous sections, the question that arises is whether

NC has a clear advantage over PF. To answer this

question, we calculated the coding gain and plotted

it in Figures 7, 8, and 9 as a function of network size,

network density, and multicast group size.

NC has an advantage over PF if it requires fewer

packet transmissions, so we divide the number of

packet transmissions under PF by the number of

packet transmissions under NC. A value of 1 indi-

cates that both approaches require the same number

of packet transmissions to deliver a data packet to

all multicast receivers. A value of 1.2, for exam-

ple, would indicate that PF requires 20% more packet

transmissions than NC under the same scenario. Con-

sider for example that we want to calculate the cod-

ing gain in a sparse network of size 90 nodes and 9

destinations. The number of required packet trans-

missions in case of PF is 11.68 which can be obtained

from Figure 1. The corresponding number of required

packet transmissions in case of NC is 10.79 which is

obtained from Figure 6. Dividing the number of re-

quired packet transmissions in case of PF by that of

NC we get 1.08 which is the value plotted in Figure 9.

This value indicates that PF requires transmitting 8%

more packets than NC.

Figures 7, 8, and 9 illustrate that NC is never

worse than PF, no matter the network density, num-

ber of nodes, or multicast group size. Using NC will

often result in a coding gain, and the gain is more pro-

nounced for larger networks, sparser networks, and

larger multicast group sizes. For multicasting to 2

destinations, NC has at best a marginal improvement

over PF (often less than 1%, with a maximum gain of

3%). For multicasting to 9 destinations, NC starts to

show a non-trivial gain for networks as small as 30

nodes. However, given the width of the conﬁdence

intervals for the individual data points, we should not

over-analyze these differences. It turns out that, for

all network sizes, multicast group sizes, and network

densities, the differences in the lower bounds are NOT

statistically signiﬁcant.

4 CONCLUSIONS

Based on our models and the results collected, it

would seem that NC is potentially advantageous, un-

less we limit ourselves to small networks (30 nodes

or less) and small multicast group sizes (5 or lower).

However, any coding scheme also introduces over-

heads: packets have to be encoded at the source, de-

coded at the receiver, and potentially recoded at in-

termediate nodes. Depending on the coding scheme

used, network coding may also increase end-to-end

latency, as a number of coded packets may have to

be received at a node before the original data pack-

ets can be reconstructed. Finally, in a network coding

scheme, losing a single coded packet may result in a

receiver being unable to recover a number of original

data packets. In deciding whether to apply PF or NC,

these factors also should be considered.

In the future work, we plan to build on these mod-

els to model/include the impact of lossy links.

REFERENCES

Ahlswede, R., Cai, N., Li, S.-Y. R., and Yeung, R. W.

(2000). Network information ﬂow. IEEE Transac-

tions on information theory, 46(4):1204–1216.

Butenko, S., Cheng, X., Oliveira, C. A., and Pardalos, P. M.

(2004). A new heuristic for the minimum connected

dominating set problem on ad hoc wireless networks.

In Recent developments in cooperative control and op-

timization, pages 61–73. Springer.

Cagalj, M., Hubaux, J.-P., and Enz, C. (2002). Minimum-

energy broadcast in all-wireless networks: Np-

completeness and distribution issues. In Proceedings

of the 8th annual international conference on Mobile

computing and networking, pages 172–182. ACM.

Egbogah, E. E., Fapojuwo, A. O., and Chan, N. (2008).

Scalable team oriented reliable multicast routing pro-

tocol for tactical mobile ad hoc networks. In IEEE,

Military Communications Conference (MILCOM).

Fomin, F. V., Grandoni, F., and Kratsch, D. (2008). Solving

connected dominating set faster than 2 n. Algorith-

mica, 52(2):153–166.

Fragouli, C., Widmer, J., and Boudec, J.-Y. L. (2008). Efﬁ-

cient broadcasting using network coding. IEEE/ACM

transactions on Networking, 16(2):450–463.

Gopinath, S. and Nagarajan, N. (2015). Energy based reli-

able multicast routing protocol for packet forwarding

in manet. Journal of applied research and technology,

13(3):374–381.

Kunz, T., Mahmood, K., and Li, L. (2012). Broadcasting

in multihop wireless networks: The case for multi-

source network coding. In IEEE, International Com-

munications Conference (ICC).

Kunz, T., Paul, S., and Li, L. (2010). Efﬁcient broadcasting

in tactical networks: Forwarding vs. network coding.

DCNET 2018 - International Conference on Data Communication Networking

In IEEE, Military Communications Conference (MIL-

COM).

Lee, S.-J., Su, W., and Gerla, M. (2002). On-demand multi-

cast routing protocol in multihop wireless mobile net-

works. Mobile networks and applications, 7(6):441–

453.

Lucile Canourgues, Jerome Lephay, L. S. and Beylot, A.-L.

(2006). Stamp: Shared-tree adhoc multicast protocol.

In IEEE, Military Communications Conference (MIL-

COM).

Lun, D. S., M

edard, M., Koetter, R., and Effros, M. (2008).

On coding for reliable communication over packet

networks. Physical Communication, 1(1):3–20.

Refaei, M. T. and Bush, J. (2014). Secure reliable group

communication for tactical networks. In IEEE, Mili-

tary Communications Conference (MILCOM).

Royer, E. M. and Perkins, C. E. (1999). Multicast opera-

tion of the ad-hoc on-demand distance vector routing

protocol. In The 5th Annual ACM/IEEE International

Conference on Mobile Computing and Networking.

Multicasting in Tactical Networks: Forwarding Versus Network Coding