Force Control of Surgical Robot with Time Delay using Model
Predictive Control
Jasmeet Singh Ladoiye
1
, Dan S. Necsulescu
1
and Jurek Sasiadek
2
1
Department of Mechanical Engineering, University of Ottawa, Ottawa, Canada
2
Department of Mechanical Engineering, Carleton University, Ottawa, Canada
Keywords: Minimum Invasive Surgery (MIS), Surgical Robots, Telecommunication, Force Feedback, Model Predictive
Control (MPC), Time Delays, Proportional-integral-derivative (PID), Bilateral Master-slave Control.
Abstract: Tele-surgical robotic systems are making our vision of “virtual open surgery” into reality by using minimum
invasive techniques with laparoscopic vision technology. The commercial available minimally invasive
robotic systems (MIRS) force the surgeons to forgo the ability to touch and feel the environment, unlike
conventional open surgery. Surgeons rely on the visual feedback from the patient’s side at the master console
to get information about the operation site. The control gets even more difficult in the teleoperated surgical
systems due to random network delays. The difference in the network delay in data and perception makes
hand to eye coordination even more difficult. Force feedback can offer surgeon instant perception of the
physical properties at the operating end. A novel approach is proposed to control the force of a surgical robot
suffering from signal delays using model predictive control. The proposed MPC-scheme of force control in
between the master and slave station shows compensation of the deterministic time delays.
1 INTRODUCTION
With the rapid advancement in technology,
telerobotic concepts play a vital role in the world of
robotic research (Tachi, Arai, and Maeda,1990),(
Buss and Schmidt,1999). Telerobotic systems
allowed a person to extend his intelligence and
manipulation skills to the remote unknown
environment. It was the leap towards the semi-
intelligent systems, by providing semiautonomous
capabilities to the system while having task controlled
by humans. Remote surgery became possible by
exploiting the capabilities of the teleoperated systems
by overcoming the barriers such as temperature,
scaling, and pressure. Force feedback is a much-
esteemed feature required by the human operator to
understand the characteristics of the unknown
environment.
Minimum Invasive Surgery (MIS) is one of the
areas where this field of telerobotics has led to
massive advancements by enlarging the human
possibilities (Ortmaier, Reintsema, Seibold, Hagan,
and Hirzinger,2001). MIS has the following
advantages over the open surgery (C. Preusche, T.
Ortmaier and G. Hirzinder ,2002):
 Shorter rehabilitation time and fast recovery
at the hospital.
 Pain reduced because of operating through
incisions.
 Cosmetical advantages due to small
incisions.
Figure 1: Conventional minimally invasive surgery (Hagn,
2011).
Figure 1 shows long slender instruments that are
used to perform MIS. These long instruments are
inserted into the patient’s body through small cuts
made on the body. The incision act as fulcrum point
about which instruments rotates, this point restricts
192
Ladoiye, J., Necsulescu, D. and Sasiadek, J.
Force Control of Surgical Robot with Time Delay using Model Predictive Control.
DOI: 10.5220/0006908601920200
In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 2, pages 192-200
ISBN: 978-989-758-321-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

the motion of the body to 4 DOF (degrees of
freedom).
MIS techniques also serve as disadvantages for
the operators (C. Preusche, T. Ortmaier and G.
Hirzinder ,2002) that are as following:
 Reduced or no tactile and force feedback
because of long instruments.
 Reduced sight.
 Tremor gets amplified because of the giant
lever arm.
 Pivot points restrict the motion.
New surgical systems have been developed such
as ZEUS-Systems (ComputerMotion, 2003) and Da
Vinci-Systems (Intuitive Systems, 2000) that are
trying to overcome these handicaps.
Teleoperation is the ability to perform the surgery
remotely, that will help the surgeon to practice it
throughout the world. The Biorobotics lab at the
University of Washington developed a RAVEN
telerobotic system ( B. H. et al., 2009) that focuses on
carrying out remote surgeries. RAVEN is operated
currently by using PHANTOM Omni controllers in
which haptic feedback is yet not developed for the
system.
Haptic feedback is a large area of interest when it
comes to medical robotics. The traditional
teleoperation one of the limitation is the lack of the
force feedback to the surgeon such that surgeon only
depends on the visual feedback to feel the force
applied to the environment.
The Technical University of Eindhoven
developed Surgeon’s Operating Force Feedback
Interface Eindhoven (SOFIE) robotic arm to improve
the haptic feedback to the Da Vinci system. SOFIE
was designed keeping following design requirements:
easier set-up times; additional DOF at the tip of the
instrument; haptic feedback and increased patient
safety ( Hannaford and Okamura, 2008).
In advanced telesurgery scenarios such as in
orthopaedic surgeries, the surgeon and robot can
share the tasks or can work on autonomous mode
under the supervision of a surgeon like ROBODOC
sold by Think Surgical Inc. ( Netravali, Borner and
Barger,2016). The robot uses Computed Tomography
(CT) scans and fiducial markers to plan the motion
using systems software.
PID controllers is widely spread in industries
owing to its simplicity and effectiveness. MPC with
the capability to predict the future enables it to cater
the large time delayed processes unlike PID (Lennox
and Lauri,2013).
In this paper, control of force using hybrid
force/position control architecture suffering from
time delay is discussed. The compensation of time
delay using MPC is discussed that arises due to the
wireless communication link in a surgical robot is
proposed making the force control even more
difficult.
In Summary, the significant contributions of this
paper are: The robustness of the MPC controller over
the PID as a force control in a teleoperated surgical
system providing force feedback at the master end.
Force feedback provides another dimension to the
surgeon to feel the environment such as the tension of
the surgical knot, the stiffness of the environment etc.
The effectiveness of the MPC has been tested out in
different constant delays. This study is limited to
surgical arms capable of performing surgery in
autonomous mode under the supervision of surgeon
such that the reference is known to them before the
operation starts.
Rest of the paper is organised as follows: The
systems control architecture construction is discussed
in section 2. MPC as a force controller along with its
control synthesis is described in section 2.1 as a part
of master end following the communication and slave
end. Section 3 shows the simulation results of the
force control using MPC and a comparison has been
presented with PID. Section 4 discusses in detail the
simulation results shown in section 3 of the paper In
the end, Section 5 and 6 describes the conclusion
along with the future work.
2 CONTROL ARCHITECTURE
Surgical robots are based on the principle of master
and slave robot. A typical teleoperated robot has three
major components: a master device (surgeon’s end),
a slave device and a communication channel
(transmission) as shown in Figure 2. Slave side is
extended affected by the tool-tissue interaction with
the unknown environment inside the human body. It
is vital to simulate a proper environment to study the
behaviours of the system in those conditions.
Systematic illustration of the operation is described as
follows:
Figure 2: Position/force control architecture for telesurgical
robot.
Force Control of Surgical Robot with Time Delay using Model Predictive Control
193

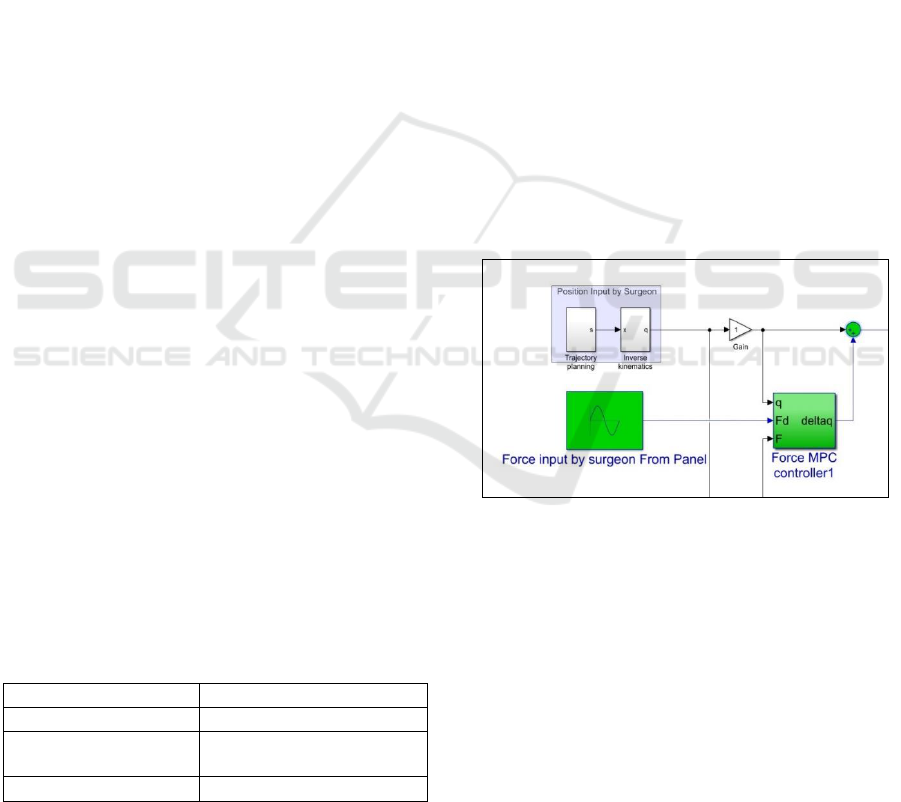
2.1 Communication System
The system responsible for the data transfer, coding
and decoding signals and other tasks to have a
communication between the two ends. A
communication system comprises a transmitter, a
receiver and a transmission medium. Latency and
signal quality depends on the subcomponents of the
system. Besides quality issues, in telesurgical
systems, data loss is one of the most critical
components to be taken care of which is best handled
by User Datagram Protocol (UDP) ( Arata, Jumpei,
Takahashi, Pitakwatchara, Warisawa, Tanoue,
Konishi and Ieiri et al., 2007). In the trans-Atlantic
surgery carried in the past, the mean signal delay was
around 155ms (Marescaux, Jacques, Leroy, Gagner,
Rubino, Mutter, Vix, Butner, and Smith, 2001). 85ms
of lag occurs in the data signals lag, but the 70ms lag
occurs in the slave side in encoding and decoding of
the visual cues. In telesurgery worked out between
Japan and Thailand (Arata, Jumpei, Takahashi,
Pitakwatchara, Warisawa, Tanoue, Konishi and Ieiri
et al., 2007), the average time delay in data was
observed around 122ms. When the average value of
random delays changes, the effects of delay gets more
pronounced.
In a study carried out (Smith and Chauhan, 2012)
to investigate the effects of the distance on the
latency. Da Vinci robotic mimic simulator was used
to get the results for studying the impact of latency.
This simulator was initialised with the actual delay
parameters of the real-time scenario. Following
observations were made:
1. The surgeons could not detect the lag time
till 200ms.
2. From 300ms to 500ms, they could detect the
lag time, but they were able to compensate
for it by pausing their movements.
3. However, after 500ms it becomes insecure
as the settling time increases for the system
as shown in Table 1.
Table 1: Observations of the Da Vinci simulator.
Time lag (milliseconds)
Effect on the system
0 – 200
Safe
200-500
Physically dependent on
the surgeon
600 - more
Unsafe
The experiments were carried out in a virtual
environment, rather than on live patients. The
effectiveness of the proposed control scheme is tested
under the deterministic time delays chosen in each of
the three intervals in Table 1 and results are compared
with the observation of the above study.
2.2 Master Model
The surgeon controls the slave end of the robot by
using a master model that is capable of visual output
from the slave end. The prime objective of this model
is to provide a realistic and accurate surgical situation
carried out in a remote site.
Figure 3 describes the principal components
comprising the master’s end. The master’s inputs are
designed like the inputs of the minimally invasive
surgical tools. The surgeon also gets visual feedback
from the slave robot that helps in effective decision
making.
A position/force control approach is used to do
the study such that the master end is responsible for
controlling the end of effectors position and force. A
hybrid approach for controlling position and force of
the end of the effector is used as shown in figure 3
such that position and force is controlled
independently. This architecture has two different
loops one for controlling force and other for position
control.
Figure 3: Design of master side.
The time delay can be controlled by a
controller in a system only if the controller can predict
the future. The feedback from the slave end suffers
from transmission delay; the master controller must
compensate for that. The proportional-integral-
derivative (PID) can only predict one step, i.e. T
d
(derivate time constant) such that the controller
becomes unstable when the time delay is more than
the time constant of the system (O’ Dwyer, 2000). An
adequate force controller should have the capability
to compensate the time delay and reach the setpoint
robustly by using prediction property. A model
predictive controller is chosen for looking ahead and
predicting the robot’s behaviour in the future and
control the force loop efficiently.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
194

2.2.1 Model Predictive Control
MPC attracts researchers because of its unique
advantages over other controllers. It is also known as
Receding Horizon Control (RHC). The MPC
performs the optimisation operation of the
performance index concerning the future control
sequences, using predictions of the output signal
based on a systems model with constraints on the
states, inputs and output. The difference in the
primary methodology of both the type of controllers
in which predicting the future is desirable while latter
only has the property to react to the past behaviours.
Model predictive control solves an optimisation
problem at each control interval to determine to
manipulate variables (MV’s) for the system until next
control interval. A quadratic problem comprises a
cost function, constraints and decisions. The cost
function is a scalar quantity that must be minimised
to at each interval to measure the controller’s
performance. Physical bounds in the form of
constraints on mv’s and plant output can be applied
to keep a check on systems performance. MV is
adjusted as per the applied constraints to satisfy the
solution.
The Cost function (1) is given by:
J(z
k
) = J
y
(z
k
) + J
u
(z
k
) + J
du
(z
k
) + J
e
(z
k
) (1)
Where z
k
is the Quadratic Problem (QP)
decision. Default weights as shown in (2), (3), (4), (5)
are applied on each term that can be varied to achieve
the objectives of the system.
J
y
(z
k
) =
 









 

 






2
(2)
J
du
(z
k
)=
 









 







 
2
(3)
J
u
(z
k
) = 
 









 









(4)
J
e
(z
k
) =




(5)
where:
k- Current control interval.
p- Prediction horizon (number of intervals)
n
y
– Number of plant output variables.
z
k
- QP decision, given by:
z
T
k
= [ u(k|k)
T
u(k+1|k)
T
….. u(k+p-1|k)
T
e
k
].
y
j
(k+i|k) – the Predicted value of j
th
plant
output at i
th
step.
r
j
(k+i|k) – Reference value for j
th
plant output
at i
th
step.
s
y
j
– output scale factor.
w
y
i,j
– Tuning weights for the plant output.
s
u
j
– input scale factor.
w
u
i,j
– tuning weight for plant input.
w
du
i,j
– tuning weight for the rate of change of
input.
e
k
- slack variable at control variable k.


– Constraint violation penalty weight.
The discrete state space format for a time
delayed is given in equations (6) and (7) (Wang,
2004):
x(k+1) = Ax(k) + B∆u(k-d) (6)
y(k) = Cx(k-d) (7)
Where:
x
i
= i-th control variable
r
i
= i-th reference variable
u
i
= i-th manipulated variable
d = (total) time delay in the system
A = 
 













B = 







C = 







x(k)
T
= 



 


∆x
p
(k) = x
p
(k) – x
p
(k-1)
At each control interval t, The process output
is predicted p-steps into the future y(t+l), where l =
1,..,p. The prediction output depends on the past
results and planned m-steps. The planned move is
evaluated by minimising a quadratic cost function.
The cost function index incorporates the error and the
actuation moves. Only u(t) is applied to the system,
and the future vector is evaluated. Prediction value is
evaluated at every step by comparing the current
values to the predicted values through the filter as
shown in Figure 4. The above-stated methods are
repeated at every control interval, that is why it is
called receding horizon control.
Force Control of Surgical Robot with Time Delay using Model Predictive Control
195

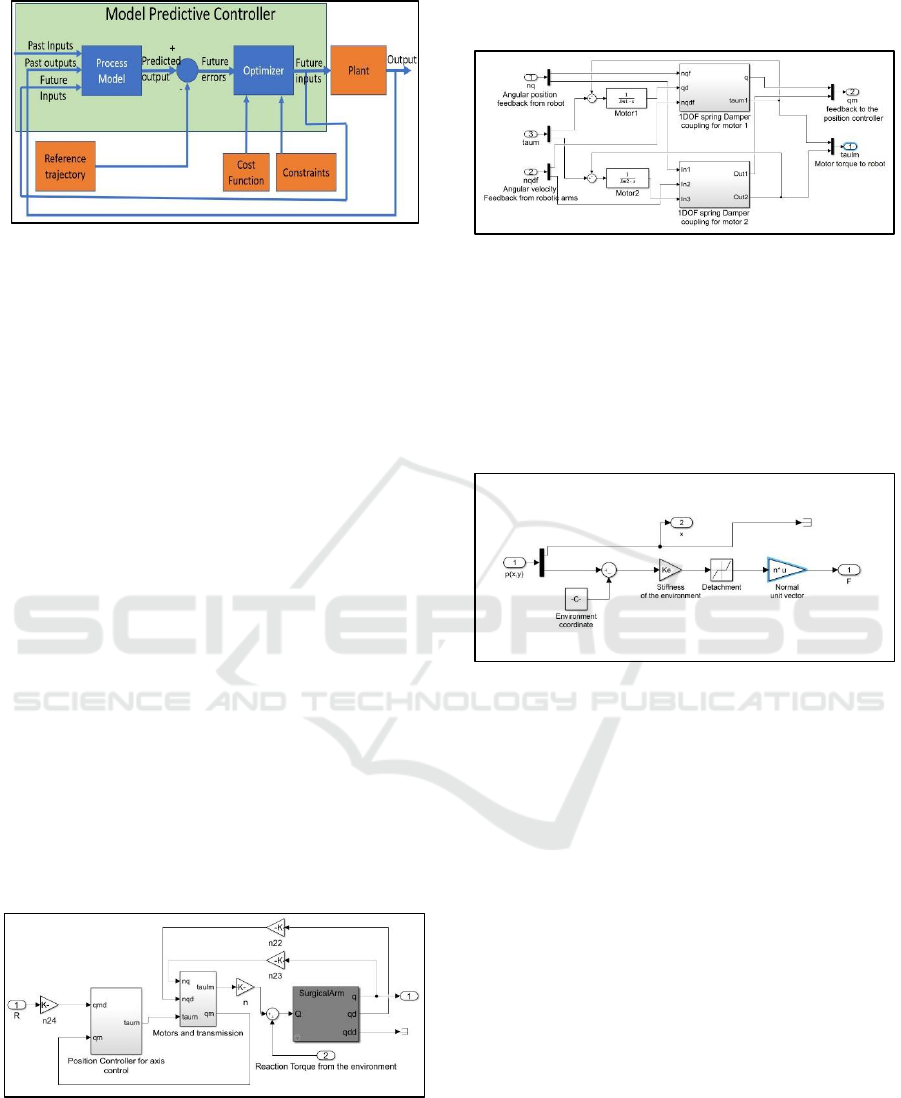
Figure 4: Model Predictive Controller.
MPC also has a “previewing” feature such that the
past information helps to predict the future
information of the system. This feature can be utilized
for the systems with known reference trajectories
such as surgical robots with the ability to perform
autonomously to compensate for the time delay. Such
information is useful because that makes the
controller prepare few steps ahead of time.
2.3 Slave Model
Functionality and safety of the patient is the most
crucial factor in the telesurgery. The accurate
kinematic and dynamic models of the robot along
with the appropriate image guidance and modelling
widely contribute towards accuracy and safety of the
system.
It is essential to know the accurate model of
the slave robot and its behaviour when it encounters
the environment. A 2 DOF dynamic model with first
order flexible joints coupling is considered for our
system.
The reaction force from the environment is
calculated in the form of reaction torque and is used
as feedforward compensation to the robot as shown in
the Simulink
TM
model of slave model in figure 5.
Figure 5: The dynamic model of the slave robot.
A 1-DOF spring damping system in the form
of Proportional-Derivative (PD) control is used as an
artificial flexible coupling for our system. Actuators
provide localised feedback to the controller. The
position controller founds the necessary driving
torque required to minimise the error.
Figure 6: Block diagram of the motor attached with
artificial coupling.
We have assumed that the slave is operating in
a known environment with a point contact interaction
model as depicted in figure 7. The robot is in free
motion initially until meets the environment. The
detachment block outputs zero value when the robot
is not in contact with the environment and gives a
nonzero value when in contact.
Figure 7: Known environment model.
A simple spring model of the environment
reaction force is given in equation (8) :
F
e
= K
e
*(x - x
e
) (8)
Where:
K
e
= Stiffness of the environment.
Y = EOF position.
y
e
= Environment position.
The following values were chosen for
simulation:
K
e
=1. e+7 [N/m ], for hard tissue
y
e
= 2.82.e-5 [m]
2.3.1 Robot Specifications
A 2-R (Revolute) degree planar robot as shown in
figure 8 is considered for the study. The dynamic
parameters of the robot as follows:
L
1
= 1 m is the length of the link 1.
L
2
= 1 m is the length of the link 2.
M
1
= 50 kg, the mass of the link 1.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
196

M
2
= 50 kg, the mass of the link 2.
ɵ
1
is the rotational angle of the joint 1.
ɵ
2
is the rotational angle of the joint 2.
Lc
1
= Lc
2
= 0.5m is the length to the mass
centre of the link.
Figure 8: Surgical arm with 2 DOF.
2.3.2 Robot Kinematics
Denavit - Hartenburg representation for the 2-R
robot is shown in table 2 below:
Table 2: D-H parameters of the 2-R robot.
Joint no.
a
i
α
i
d
i
ɵ
i
1.
L
1
0
0
ɵ
1
2.
L
2
0
0
ɵ
2
2.3.3 Robot Dynamics
Forward kinematic equations (9), (10), (11), (12) of
the 2-R robot are described as follows:

1
=
1
sin
1
(9)

1
=
1
cos
1
(10)

2
=
1
sin
1
+ 
2
sin (
1
+
2
) (11)

2
=
1
cos
1
+ 
2
cos (
1
+
2
) (12)
The general form of the equation of robot is described
in (13):
H(q
̈
)+ C(q
̇
, q)+ g(q)= M + J
T
.F (13)
Where:
H(q
̈
): is the inertia matrix of the system
C (q
̇
, q): Coriolis and Centrifugal forces
G(q): gravitational components
M: Torque of the system
J
T
: transpose of the Jacobian
F: Force at the EOF
Table 3 shows the dynamic parameters of the
system simulation (Rocco, Paolo, Gianni Ferretti, and
Magnani, 1996)
Table 3: Dynamic parameters of the system.
Sr.
No
Parameters
Values
1.
Moment of inertia of the
motors(Jm
1
)
5.e-3 kg.m
2
2.
Moment of inertia of the
motors(Jm
2
)
2.e-3 kg.m
2
3.
Stiffness for coupling (Kel
1
)
70 Nm
-1
4.
Stiffness for coupling (Kel
2
)
70 Nm
-1
5.
Viscous damping (del
1
)
0.05 Nsm
-1
6.
Viscous damping (del
2
)
0.05 Nsm
-1
7.
Reduction ratio
100
3 SIMULATION RESULTS
Let’s consider the robot initially at a steady state with
the initial conditions described in Table 4, in a lower
elbow posture. The environment is supposed to be
known and frictionless such that robot will apply
force on the negative y-direction while moving
parallel to the x-axis (for 30 cm) with a trapezoidal
velocity profile with a maximum velocity of 3 mm/s
in 15 seconds.
Table 4 shows the initial conditions of the arm
for the simulation.
Table 4: Initial conditions of the arm.
Sr.
No
Parameter
Initial condition
1.
Initial motor position
(qm0)
[-147.06,294.12]
rad
2.
End of effector position
[0.2,0] m
3.
Initial link position (q0)
[-1.47,2.94] rad
The robot was tested with different constant
time delays as suggested (Smith and Chauhan, 2012),
in Table 1.
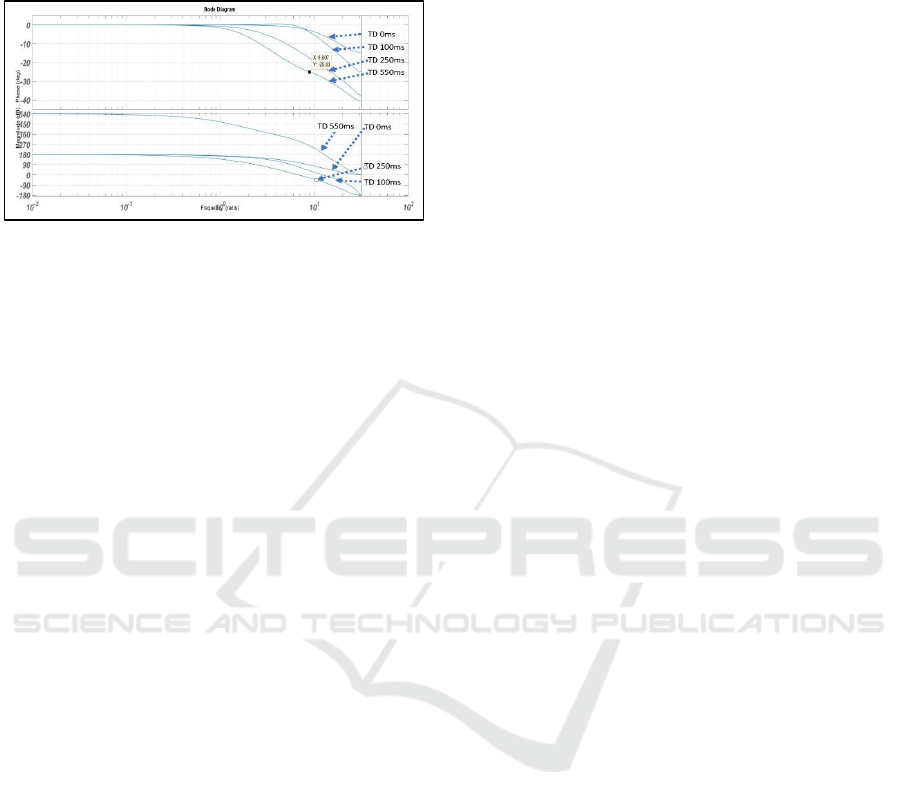
Figure 9 illustrates that with the increase in the
dead time, oscillations in the system increases that is
controlled by tuning the weights of MPC to get an
overshoot free system. The response of the system
gets slower as the weights are made less aggressive
with the increase of time delay. Overshoot of less than
10% was observed with the time delay of 100ms
when using MPC for specific tuning weights of MPC
with no time delay are used.
Force Control of Surgical Robot with Time Delay using Model Predictive Control
197

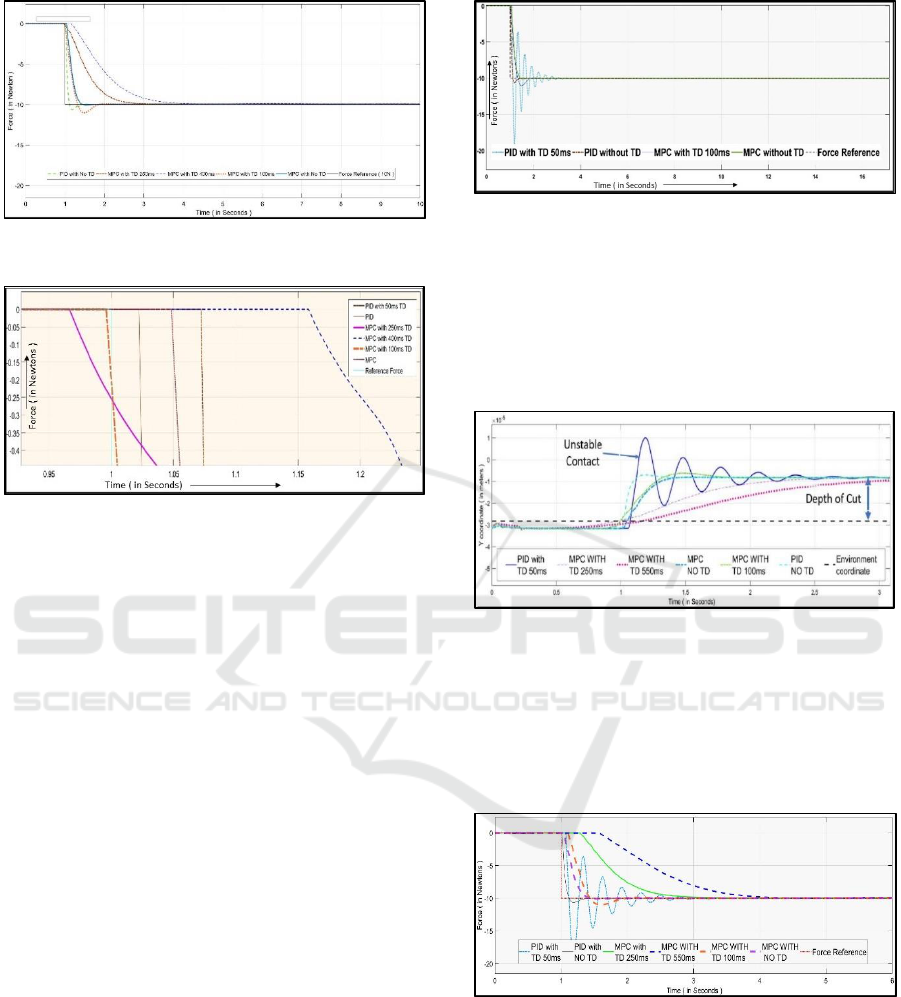
Figure 9: MPC (with previewing) with a different time
delay with 10
7
N/m stiffness.
Figure 10: Panned view of Figure 8 around time stamp 1
second when force starts acting on the system.
Figure 10 shows that previewing can help to
compensate for the effect of dead time in the system
as we can see that MPC is prepared for the dead time
ahead of its time. All the responses with different time
delays are tuned for previewing in such a way that
makes their response close to the reference of the
system showing no or minimal dead time effect on the
reaction of the force control. Previewing could be
used for the case of surgical robots capable to operate
in autonomous mode since the reference is known to
them. MPC previews the reference to make the
system closed to delayed free system when the time
delay is deterministic as shown.
Figure 11 presents a comparison of PID
controller vs MPC with time delay. PID results in a
highly oscillatory response with the time delay of
100ms and hence making the system unstable.
Therefore, the time delay of 50ms is considered for
PID to compare with MPC with dead time 100ms.
The system's response with PID is oscillatory and
cannot be damped by changing the tuning parameters.
MPC has shown its robustness as compared to PID
with double the time delay.
Figure 11: Comparison of MPC vs PID with time delay.
Figure 12 shows the position of the surgical
arm in Y plane versus time. It compares the type of
contact robot is making in the presence of time delays
with MPC and PID controllers. PID with the time
delay shows oscillatory contact with the environment
versus stable contact by MPC under different time
delays.
Figure 12: Position of the robot vs time.
In the situation when no previewing is
available, the dead time cannot be compensated by
using MPC. The effects of dead time are neutralised
by the MPC unlike PID as shown in figure 13 but a
time lag exists in the system unlike with previewing.
The simulation results show that the system is stable
under the control of MPC.
Figure 13: MPC vs PID with different time delays with no
previewing.
Figure 14 shows the frequency analysis of the
system with different time delays by using bode plot.
The phase lag increases with the increase of the time
delay as described in the above figure with an
increase in frequency. The time delays considered in
the system are approximated by using Padé
approximation technique. Increasing the frequency of
the system increases the computational load on the
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
198

system increases demanding for more computation
power. Since the system gets the linearised system is
controllable even when the frequency is increased.
Figure 14: Bode plot for the system under different time
delays.
4 DISCUSSIONS
 MPC as a force controller can be used to develop
haptic feedback in a surgical system suffering
from time delays.
 The approach’s effectiveness was tested in
different scenarios and results were compared
with the observations of the previous work by
researchers. MPC shows a stable response in all
the scenarios.
 MPC can be used even when the time delay is
more significant than 500ms and shows the
system is robust enough to carry out the surgery.
The response of the system gets slower when
time delay goes beyond 500ms increasing total
time to carry out the operation.
 Previewing can be used to compensate for the
dead time using MPC when reference is known.
The response of the system is closer to a delay-
free system in that case. This feature can be used
in surgical robots with the capability of
performing in autonomous mode.
5 FUTURE WORK
Introducing impact and velocity model into the
system to have a zero-impact velocity during the
contact is the proposed future work. Such work will
also show the more considerable difference in the
performance of MPC over PID. Gain scheduling
using MPC can help to handle the system with
random delays.
6 CONCLUSIONS
In this paper, force feedback by using Model
Predictive Control (MPC) for surgical robots was
developed and discussed that will give an extra
dimension to the existing surgical systems. MPC can
compensate the time delays when the delays are
known by previewing. The goal is to design control
signal at each sampling time k such that state
feedback law minimises the cost function to
constraints of control input. The benefit of using the
previewing in case of known references helps
controller to predict the delayed free future.
Simulation experiments show the effectiveness of the
concept.
REFERENCES
Tachi, S., Arai, H. & Maeda, T., 1990. Tele-existence
master-slave system for remote manipulation. II. 29th
IEEE Conference on Decision and Control, pp.85–90.
Buss, M. & Schmidt, G., 1999. Control Problems in Multi-
Modal Telepresence Systems. Advances in Control,
pp.65–101.
Ortmaier, T., Reintsema, D., Seibold, U., Hagn, U. and
Hirzinger, G., 2001. The DLR minimally invasive
robotics surgery scenario. Hieronymus
Buchreproduktions GmbH, München Proceedings.
Preusche, C., Ortmaier, T. and Hirzinger, G., 2002.
Teleoperation concepts in minimal invasive
surgery. Control engineering practice, 10(11), pp.1245-
1250.
Lanfranco, A.R., Castellanos, A.E., Desai, J.P. and Meyers,
W.C., 2004. Robotic surgery: a current
perspective. Annals of surgery, 239(1), p.14.
Guthart, G.S. and Salisbury, J.K., 2000. The Intuitive/sup
TM/telesurgery system: overview and application.
In Robotics and Automation, 2000. Proceedings.
ICRA'00. IEEE International Conference on (Vol. 1,
pp. 618-621). IEEE.
Hannaford, B., Friedman, D., King, H., Lum, M., Rosen, J.
and Sankaranarayanan, G., 2009. Evaluation of
RAVEN surgical telerobot during the NASA extreme
environment mission operations (NEEMO) 12
mission. Electrical Engineering Department,
University of Washington, SeattleTech. Rep, 2.
Hannaford, B. and Okamura, A.M., 2008. Chapter 30:
Haptics, Handbook of Robotics.
Arata, J., Takahashi, H., Pitakwatchara, P., Warisawa, S.I.,
Tanoue, K., Konishi, K., Ieiri, S., Shimizu, S.,
Nakashima, N., Okamura, K. and Fujino, Y., 2007,
April. A remote surgery experiment between Japan and
Thailand over Internet using a low latency CODEC
system. In Robotics and Automation, 2007 IEEE
International Conference on (pp. 953-959). IEEE.
Marescaux, J., Leroy, J., Gagner, M., Rubino, F., Mutter,
D., Vix, M., Butner, S.E. and Smith, M.K., 2001.
Force Control of Surgical Robot with Time Delay using Model Predictive Control
199

Transatlantic robot-assisted
telesurgery. Nature, 413(6854), p.379.
Smith, R. and Chauhan, S., Using simulators to measure
communication latency effects in robotic telesurgery.
Wang, L., 2004. A Tutorial on Model Predictive Control:
Using a Linear Velocity‐Form Model. Asia‐Pacific
Journal of Chemical Engineering, 12(5‐6), pp.573-614.
Hagn, U., 2011. The aspect of versatility in the design of a
lightweight robot for surgical applications (Doctoral
dissertation, DLR).
Netravali, N.A., Börner, M. and Bargar, W.L., 2016. The
Use of ROBODOC in Total Hip and Knee Arthroplasty.
In Computer-Assisted Musculoskeletal Surgery (pp.
219-234). Springer, Cham.
O'Dwyer, A., 2000, January. PID compensation of time
delayed processes: a survey. In Conference papers (p.
44).
Rocco, P., Ferretti, G. and Magnani, G., 1997. Implicit
force control for industrial robots in contact with stiff
surfaces. Automatica, 33(11), pp.2041-2047.
Sha'aban, Y.A., Lennox, B. and Laurí, D., 2013. PID versus
MPC performance for siso dead-time dominant
processes. IFAC Proceedings Volumes, 46(32),
pp.241-246.
UKEssays. November 2013. Zeus Robotic Surgical System
Information Technology Essay. [online]. Available
from: https://www.ukessays.com/essays/information-
technology/zeus-robotic-surgical-system-information-
technology-essay.php?vref=1 [Accessed 26 June
2018].
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
200