
Learning Plaintext in Galbraith’s LWE Cryptosystem
Tikaram Sanyashi, Sreyans Nahata, Rushang Dhanesha and Bernard Menezes
Indian Institute of Technology Bombay, Powai, Mumbai, India
Keywords:
Learning with Errors, Linear Programming, Integer Linear Programming, Galbraith’s Binary LWE.
Abstract:
Unlike many widely used cryptosytems, Learning with Errors (LWE) - based cryptosystems are known to be
invulnerable to quantum computers. Galbraith’s Binary LWE (GB-LWE) was proposed to reduce the large key
size of the original LWE scheme by over two orders of magnitude. In GB-LWE, recovering the plaintext from
the ciphertext involves solving for the binary vector x
x
x in the equation x
x
xA
A
A = b
b
b (A
A
A, a 640 ×256 binary matrix and
b
b
b, a 256 element integer vector are knowns). Previously, lattice-based attacks on binary matrices larger than
400 × 256 were found to be infeasible. Linear programming was proposed and shown to handle significantly
larger matrices but its success rate for 640 × 256 matrices was found to be negligible. Our strategy involves
identification of regimes L, M and H within the output (based on LP relaxation) where the mis-prediction rates
are low, medium or high respectively. Bits in the output vector are guessed and removed to create and solve a
reduced instance. We report extensive experimental results on prediction accuracy and success probability as
a function of number of bits removed in L, M and H. We identify trade-offs between lower execution time and
greater probability of success. Our success probability is much higher than previous efforts and its execution
time of 1 day with 150 cores is a partial response to the challenge posed in (Galbraith, 2013) to solve a random
640 × 256 instance using “current computing facilities in less than a year”.
1 INTRODUCTION
Introduced by Regev (Regev, 2005) in 2005, Learning
with Errors (LWE) is a problem in machine learning
and is as hard to solve as certain worst-case lattice
problems. Unlike most widely used cryptographic al-
gorithms, it is known to be invulnerable to quantum
computers. It is the basis of many cryptographic con-
structions including identity-based encryption (Cash
et al., 2010), (Agrawal et al., 2010), oblivious transfer
protocols (Peikert et al., 2008), homomorphic encryp-
tion (Brakerski and Vaikuntanathan, 2014), (Braker-
ski et al., 2014) and many more.
The LWE cryptosystem performs bit by bit en-
cryption. The private key, s
s
s, is a vector of length n
where each element of s
s
s is randomly chosen over Z
q
,
q prime. The corresponding public key has two com-
ponents. The first is a random m × n matrix, A
A
A, with
elements over Z
q
and with rows denoted a
a
a
T
i
. The sec-
ond component is a vector, b
b
b, of length m where the i
th
element of b
b
b is a
a
a
T
i
s
s
s + e
i
(mod q). The e
i
’s are drawn
from a discretized normal distribution with mean 0
and standard deviation σ.
To encrypt a bit, x, a random binary vector
(nonce), u
u
u, of length m is chosen. This is a per-
message ephemeral secret. The ciphertext is (c
c
c
1
, c
2
)
where c
c
c
T
1
= u
u
u
T
A
A
A (mod q) and c
2
= u
u
u
T
b
b
b+xbq/2c (mod
q). A received message is decrypted to 0 or 1 depend-
ing on whether c
2
− c
c
c
1
s
s
s is closer to 0 or bq/2c.
To thwart various lattice-based attacks, Lindner
et al. (Lindner and Peikert, 2011) suggested the
values of 256, 640 and 4093 respectively for n, m
and q leading to a public key of size approximately
250 Kbytes. This unacceptable storage overhead for
resource-constrained devices motivated consideration
of binary values in matrix A
A
A.
Galbraith (Galbraith, 2013) studied a ciphertext-
only attack on the GB-LWE scheme to recover the
plaintext. Given c
c
c
1
= u
u
u
T
A
A
A and A
A
A, the challenge is to
obtain u
u
u
T
. Once u
u
u
T
is known, the plaintext x can be
easily computed from c
2
. Because u
u
u
T
is binary, ob-
taining its value is equivalent to finding the rows of
A
A
A that sum to c
c
c
1
, i.e. the Vector Subset Sum (VSS)
problem. (Galbraith, 2013) studied lattice-based at-
tacks on GB-LWE and concluded that such attacks
were infeasible for m >400.
(Galbraith, 2013) also posed two challenges. The
first of these was to be completed on an ordinary PC
in one day and involved computing u
u
u
T
given a random
400×256 binary matrix A
A
A and c
c
c
T
1
= u
u
u
T
A
A
A. The second
problem was the same but with a random 640 × 256
binary matrix to be solved in one year with “cur-
Sanyashi, T., Nahata, S., Dhanesha, R. and Menezes, B.
Learning Plaintext in Galbraith’s LWE Cryptosystem.
DOI: 10.5220/0006909405590565
In Proceedings of the 15th Inter national Joint Conference on e-Business and Telecommunications (ICETE 2018) - Volume 2: SECRYPT, pages 559-565
ISBN: 978-989-758-319-3
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
559

rent computing facilities”. Herold et al. (Herold and
May, 2017) responded to the first challenge success-
fully by formulating VSS as a problem in Linear Pro-
gramming (LP) and/or Integer Linear Programming
(ILP). However, for m>490, the success rate of this
approach dropped greatly. Our goal is to address the
second of these two challenges with a much higher
success rate and execution time of roughly 1 day.
The main contribution of this paper is the outline
of a strategy wherein we attempt to solve a given in-
stance of the VSS problem by guessing some of the
bits in the unknown vector u
u
u
T
. We remove these to
create and solve a reduced instance or sub-instance
of the original problem. Using LP as in (Herold and
May, 2017), we obtain fractional solutions for m>2n
in particular. Rounding the solutions to 0 or 1 results
in a mis-prediction rate of about 20% on average for
m = 640. We identify regimes L, M and H within
the predicted solution vector where the mis-prediction
rates are low, medium or high respectively. It is nec-
essary to carefully choose the bits in u
u
u
T
for removal
since a valid sub-instance can only be created by re-
moval of bits that are all correctly guessed. This sug-
gests choosing bits in regime L. However, extensive
experiments conducted by us led to the conclusion
that the resulting sub-instance is hard to solve even
if the size of the sub-instance is greatly reduced. In-
deed it is best to remove bits in H but the correctness
of their predicted values is hardest to guarantee.
We report results on both, prediction accuracy and
success probability as a function of number of bits
removed in L, M and H. We also experimented with
simultaneously removing bits in multiple regimes. Fi-
nally, we categorize instances into classes A, B and C
based merely on the LP output and with no knowledge
of the ephemeral secret. A Class A instance will, in
general, have a lower mis-prediction rate and can be
solved with far less computational effort.
Our convention is to represent a vector in lower-
case bold and a matrix in uppercase bold. A row vec-
tor, v
v
v, is represented as v
v
v
T
.
The rest of the paper is organized as follows. Sec-
tion 2 contains a brief background including related
work. Section 3 outlines our approach and contains
results of experiments on mis-prediction rates and
success probabilities obtained by removing bits in dif-
ferent regimes. Section 4 includes an explanation of
our main results, suggests certain optimizations and
presents a classification of instances. Section 5 con-
tains the conclusion.
2 BACKGROUND AND RELATED
WORK
(Regev, 2005) proposed LWE - a lattice based hard
problem. To reduce the key size in the original LWE
problem, the ring LWE cryptosystem was studied in
(Lyubashevsky et al., 2010) and was also shown to be
as hard as worst case lattice problems. Another vari-
ant of the LWE problem known as Binary-LWE (Mic-
ciancio and Peikert, 2013) was later proposed. Here,
the secret is a binary string instead of a string of in-
tegers modulo q. It results in smaller cryptographic
keys without compromising theoretical security guar-
antees. Hardness of B-LWE problem was proved the-
oretically in (Micciancio and Peikert, 2013). (Bai and
Galbraith, 2014) concluded that a key size of 440 is
sufficient to make B-LWE as secure as the LWE prob-
lem with key size 256. Later another variant of LWE
problem, GB-LWE was studied in (Galbraith, 2013)
for devices with low storage capacity. In this case,
both the matrix A
A
A and secret vector s
s
s are binary which
further reduces the size of the public key.
For m = 640, n = 256 and q = 4093, the LWE
crypto scheme provides security equivalent to AES-
128 (Lindner and Peikert, 2011). With these param-
eters, the total size of the public key is 640(256 +
1)log
2
(4093) = 246.7 Kbytes. However, this is far
higher than the size of the RSA or ECC public keys
which are less than 1 Kbyte. In GB-LWE, the binary
matrix A
A
A is not stored but is generated on the fly using
a PRNG with a 256 bit seed (Coron et al., 2012). In
this case, we just need to store the seed and the vector
b
b
b, which require 256+640log
2
(4093) = 7935 bits - a
considerable reduction over LWE with non-binary A
A
A.
A lattice-based attack on GB-LWE was launched
in (Galbraith, 2013) wherein an m-dimensional lattice
was constructed with the columns of A
A
A as its basis
vectors. The problem of finding u
u
u
T
was mapped to the
Closest Vector Problem with target vector, b
b
b. It was
concluded that for m >400, the attack was infeasible.
(Herold and May, 2017) studied the application of
LP and ILP to obtain u
u
u
T
. They obtained results for
n = 256 and m ranging from 400 to 640 for 1000 in-
stances. The execution of a particular instance using
ILP was aborted if it failed to obtain a solution within
10 seconds. The success probability dropped from
100% at m = 490 to 1% at m = 590. Under certain
mild assumptions, they also proved that the solution
with LP relaxation for m ≤ 2n is unique. For any
given instance they computed a score which quanti-
fies the search space for the ILP . 2
19
instances of
GB-LWE were generated for m = 640. From this en-
semble, 271 weak instances were identified. 16 of
these were solved within half an hour each.
SECRYPT 2018 - International Conference on Security and Cryptography
560
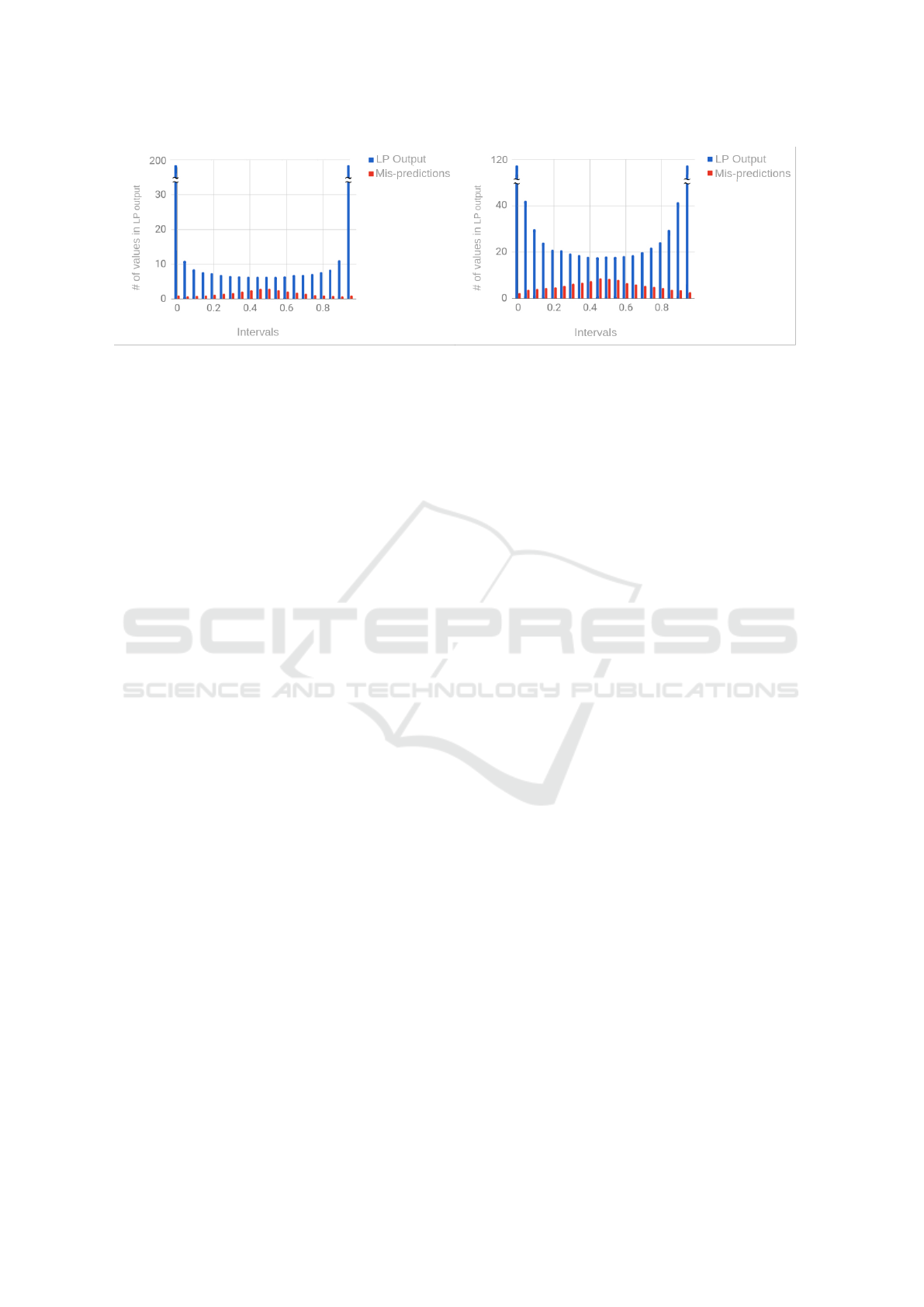
(a) 256 × 512 (b) 256 × 640
Figure 1: Distribution of LP output values and corresponding number of mis-predictions(averaged over 1000 instances).
3 OUR APPROACH
Our goal is to reduce the size of a given problem in-
stance by making accurate estimates of various bits
in u
u
u
T
and then creating a smaller sub-instance by re-
moving those bits from u
u
u
T
, removing the correspond-
ing rows of A
A
A and re-computing the new value of
c
c
c
1
. Formally, if the values of the guessed bits are
x
i
1
,x
i
2
, .. .,x
i
r
in positions i
1
,i
2
, .. .,i
r
, then those bits
are removed from u
u
u
T
, row vectors, a
a
a
i
1
,a
a
a
i
2
, ...,a
a
a
i
r
in
A
A
A are removed and the new value of c
c
c
1
is computed
as
c
c
c
0
1
= c
c
c
1
−
∑
i=i
1
,i
2
,...,i
r
x
x
x
i
∗ a
a
a
i
(1)
We then use either LP or ILP to solve for the remain-
ing bits in u
u
u
T
.
In (Herold and May, 2017) , the VSS problem was
formulated as an LP problem with the following con-
straints
A
A
A
T
u
u
u ≤ c
c
c
1
−A
A
A
T
u
u
u ≤ −c
c
c
1
u
i
≤ 1, 1 ≤ i ≤ m
u
i
≥ 0, 1 ≤ i ≤ m
Using information-theoretic arguments, (Herold
and May, 2017) concluded that the above constraints
resulted in a unique integral solution for m ≤ 1500.
Using the above formulation, we experimented
with over 1000 instances each for values of m equal
to 512 and 640. Our experiments were conducted on
an Intel i5 3.5 GHz quad core system running Ubuntu
16.04. All the programs were written in MATLAB
2015 and its inbuilt functions for LP and ILP solver
were used. For m = 512, the LP solver provided the
correct integral solution for u
u
u
T
about 50% of the time.
In the remaining 505 instances, the LP solver pro-
vided fractional outputs which were rounded to obtain
a prediction of each element in u
u
u
T
. Since the correct
value of u
u
u
T
was not obtained, we used the ILP solver
to obtain a solution. Of the 505 instances, 395 were
solved within 30 seconds. Of the remaining, 67 took
less than 10 minutes and 23 took between 10 minutes
and 2 hours. The remaining 20 could not be solved
by ILP even with maximum time configured to be 2
hours. For m = 640, neither LP nor ILP gave a correct
solution for even a single instance.
Figure 1(a) shows the average number of values
in the LP output lying in each interval of width 0.05
between 0 and 1 for m = 512. About 75% of the val-
ues lie in the intervals [0,0.05] or [0.95, 1]. Figure
1(a) also shows the number of bits incorrectly pre-
dicted from the LP output. Note that the percentage
of incorrectly predicted bits increases greatly as the
LP output value tends to 0.5. Figure 1(b) shows the
corresponding plot for m = 640. Note that the general
trend of higher number of LP output values at the ex-
treme ends of the spectrum and an increasing percent-
age of mis-predictions towards 0.5 remain similar.
However, the average percentage of mis-predictions
is much larger for m = 640 in every interval. Overall,
the average percentage of incorrectly predicted bits is
5% with m = 512 versus 20% with m = 640.
Our goal is to remove bits in u
u
u
T
to create a smaller
sub-instance via Equation. 1. Based on error proba-
bility alone (Figure 1), it should seem that removing
bits most strongly predicted to be either 0 or 1 is the
right strategy. However, another crucial factor is the
effectiveness of bit removal as a function of the LP
output value. For ease of explanation, we re-arrange
the bits in u
u
u
T
in increasing order of the proximity of
the LP output value to 0.5 (thus the rightmost bits are
closest to 0.5). Under consideration are removal of
bits in three different regimes - L, M and H (i.e. Low
error, Moderate error and High error regimes).
The elements to be removed are split into clusters
- each cluster, typically, resides in one of the regimes
Learning Plaintext in Galbraith’s LWE Cryptosystem
561
L, M or H. A regime may also contain multiple clus-
ters. A cluster is characterized by a common mis-
prediction rate for each of its elements. If there are s
elements in a cluster with mis-prediction rate e, then
there are likely to be about e
0
= ds ∗ ee mis-predicted
elements in that cluster.
The predicted values of the elements in a cluster
may be laid out in an s-bit binary string. The actual
value of the binary string is likely to be within a Ham-
ming distance of e
0
from the string. Thus it is expected
that there are
∑
e
0
i=0
s
i
possibilities for the actual value
of that string. In a similar manner, we can estimate the
number of possibilities for values in the other clus-
ters under consideration. The true value of the bits
proposed to be removed would likely be contained in
the Cartesian product of the sets of strings derived for
each cluster. For each value of the removed bits in the
Cartesian product, we create a separate sub-instance
and attempt to solve it using the ILP solver subject to
a maximum stipulated time. We proceed this way us-
ing each combination of values in the Cartesian prod-
uct until we obtain a solution or until all values in the
Cartesian product have been processed.
Note that the above procedure does not guaran-
tee that the actual values of the removed bits is con-
tained in the Cartesian product. This is because the
estimated mis-prediction rate is an experimentally de-
termined average over thousands of randomly gener-
ated instances and specific instances may have higher
mis-prediction rates in the chosen sets together with
local variations.
We experimented with creating sub-instances by
removing bits in different regimes of u
u
u
T
and solved
them within a stipulated time. We consider an ex-
periment a success if application of ILP on the sub-
instance resulted in obtaining the correct values of all
bits in the reduced u
u
u
T
within a stipulated time. Ta-
bles 1, 2, 3 show the success probability as a function
of number of bits removed and the specific regime(s)
involved, with 1000 instances.
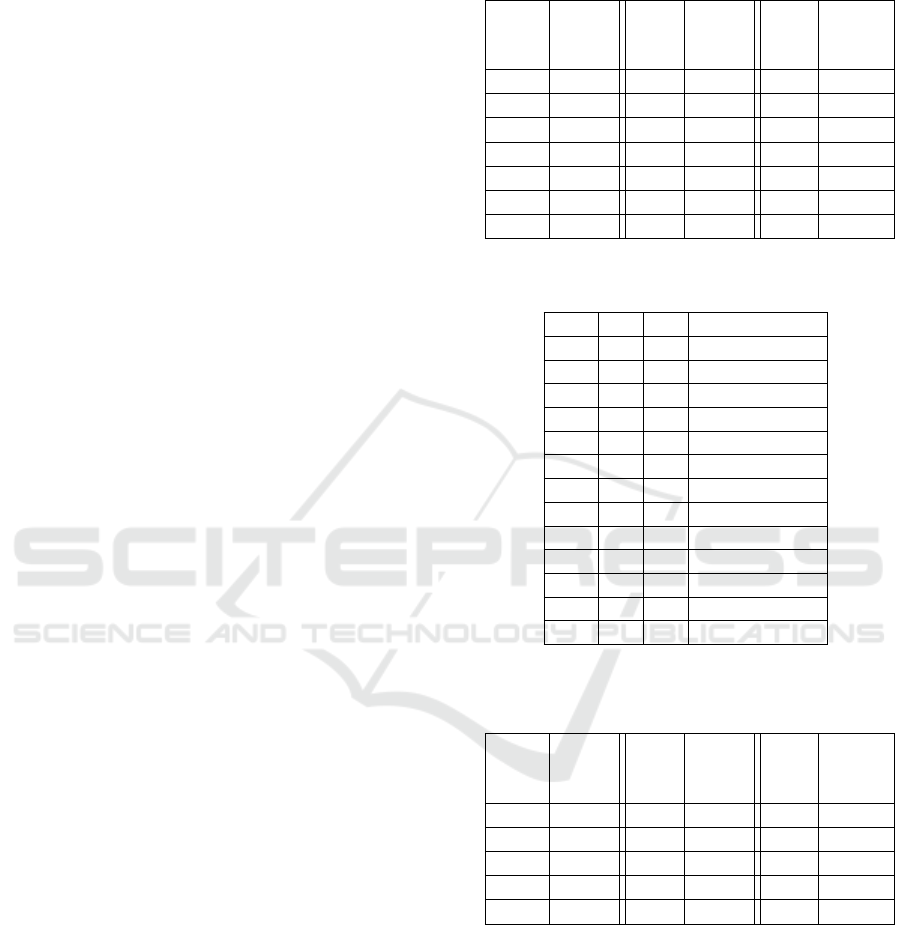
Table 1 shows that removing the rightmost 50 bits
in H succeeds in creating a solvable instance about
20% of the time but removing 50 bits starting at po-
sition 300 from the left of u
u
u
T
(in Regime M) resulted
in average success rate of only 2%. Removing the
leftmost 50 bits in u
u
u
T
(in Regime L) failed to create a
solvable sub-instance in every case. To achieve 20%
success, we need to remove about 70 bits in M or 220
bits in L. For a given number of bits, it is most effec-
tive to remove bits in H, less effective to remove bits
in M and least effective to remove bits in L.
Table 2 shows the effect of removing bits in mul-
tiple regimes. Removing 25 bits in H resulted in 1%
success (Table 1). The same effect can be obtained
Table 1: Success Probability as a function of number of bits
removed in a single regime (m = 640, ILP).
L
Succ.
Prob.
%
170 0.7
180 1.2
190 2.3
200 4.9
220 20.2
250 75.9
280 99.7
M
Succ.
Prob.
%
30 0.6
40 1.2
50 2
60 4.6
80 26.0
100 72.8
150 100
H
Succ.
Prob.
%
20 0.5
25 1.0
30 1.8
40 5
50 20.3
70 68.1
120 100
Table 2: Success Probability as a function of number of bits
removed in multiple regimes (m = 640, ILP).
L M H Succ. Prob. %
140 20 - 1.2
140 40 - 7.6
160 20 - 3.5
160 40 - 27.4
180 - 5 2.7
200 - 5 6.4
220 - 5 38.7
220 - 10 56.8
- 40 5 1.3
- 30 10 1
- 40 10 2.2
120 20 5 1
120 20 10 2.3
Table 3: Success Probability as a function of number of bits
removed in a single regime (m = 640, LP).
L
Succ.
Prob.
%
210 1.0
230 5.1
240 11.3
250 24.5
320 100
M
Succ.
Prob.
%
60 1.0
85 5.0
90 12.2
100 26.5
160 100
H
Succ.
Prob.
%
35 1.0
55 5.2
60 12.4
65 24.3
150 100
by removing only 10 bits in H together with 30 bits in
M or 5 bits in H together with 20 bits in M and 120
bits in L. Finally, Table 3 shows the effect of applying
LP rather than ILP to a sub-instance. In general, ILP
is far more likely to solve a sub-instance, although its
execution time is considerably higher.
SECRYPT 2018 - International Conference on Security and Cryptography
562
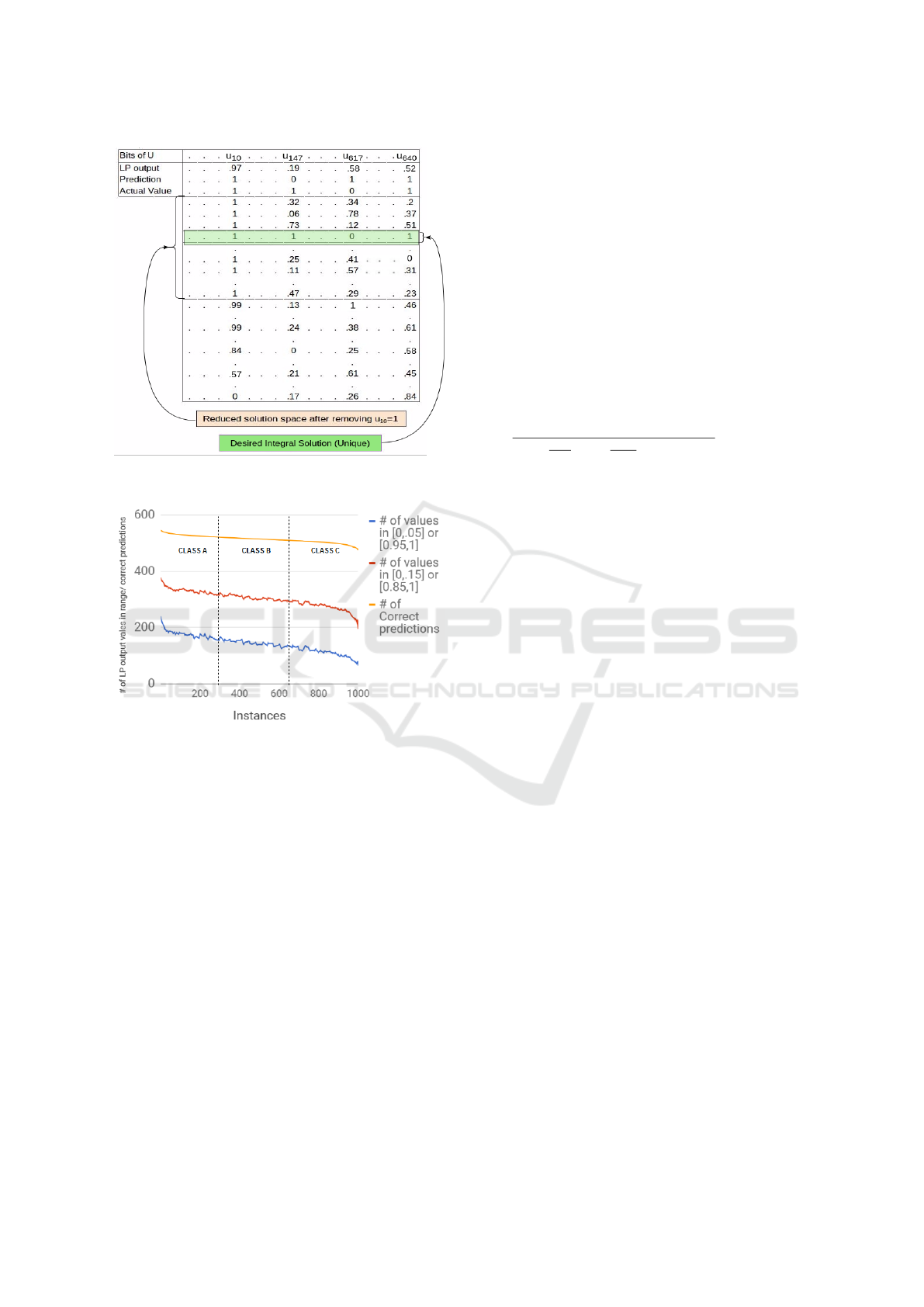
Figure 2: Illustrating solution space reduction by removing
a bit of u
u
u
T
.
Figure 3: Instance Classification with 3 metrics.
4 RESULTS, ANALYSIS AND
DISCUSSION
We first present our results, then suggest metrics to
classify instances and finally propose an optimization.
4.1 Results and Interpretation
For m = 512, of the 1000 instances considered, the
ILP solver was unable to provide a solution to only 43
instances within 10 minutes. In each of these cases,
we removed the 5 rightmost bits in Regime H. These
bits are likely to be 0 or 1 with nearly equal probabil-
ity. So, we iterated over all 2
5
= 32 combinations of
those bits, i.e., we removed each combination of those
5 bits and applied ILP to the resulting sub-instance
setting the timeout period to 10 seconds. We suc-
ceeded in 23 of the 43 cases with average execution
time less than 3 minutes. Of the remaining 20 cases,
18 succeeded by removing the rightmost 10 bits while
two required the removal of 15 bits.
In the case of m = 640, the ILP solver did not suc-
ceed in even a single case. As in the case of m = 512,
we experimented with removal of the rightmost bits in
Regime H. For each instance, we first removed 20 bits
iterating over all 2
20
combinations of them. We con-
figured the ILP package to time out after 30 seconds.
Five instances out of 1000 yielded the correct value of
u
u
u
T
for a success probability of 0.5%. On average, the
solution (if it could be found) would be obtained after
2
19
iterations. So, the execution time on 150 cores is
estimated to be
2
19
iterations × 30 sec
3600
sec
hour
× 24
hours
day
× 150 cores
∼ 1 day
If 30 bits at the rightmost end of Regime H were
removed, the success rate would increase to nearly
2% at the expense of a greatly increased execution
time of 50 days with 3000 cores.
Table 2 suggests that removing bits in multiple
regimes greatly improves the success rate. However,
in general, we require removal of larger sets of bits
in M and a much larger set of bits in L. Despite the
smaller mis-prediction rates, the total number of bits
in error is large. This requires iterating over a large
number of combinations of values. Since the total
number of possible values is multiplicative in the car-
dinalities of the chosen sets of strings, we end up with
prohibitive execution times.
We next present an explanation of our results
based on a possible interpretation of the LP output.
There are an infinite number of solutions to u
u
u
T
A
A
A = c
c
c
1
in the interval [0, 1] though the LP solver outputs only
a single solution. It follows from the linearity of this
equation that the average of any set of solution vec-
tors is also a valid solution. Because of the way the
LP solver works, its output may be thought of as a
reasonable approximation to the average of all solu-
tions.
One can consider a finite subset of all solutions by
rounding to say 10 decimal places. Figure 2 enumer-
ates these solutions. The first three rows show the LP
output before and after rounding and the actual values
of the elements in u
u
u
T
. The elements in u
u
u
T
(columns)
are arranged in increasing order of their proximity to
0.5 while the solution vectors (rows) are listed in de-
creasing order of the value of u
10
. The value of a bit,
u
i
in u
u
u
T
obtained from the LP solver can be thought
of as the approximate average of the values in that
column.
If a sub-instance is created by removing bit u
10
,
the solution space now contains only those vectors
Learning Plaintext in Galbraith’s LWE Cryptosystem
563
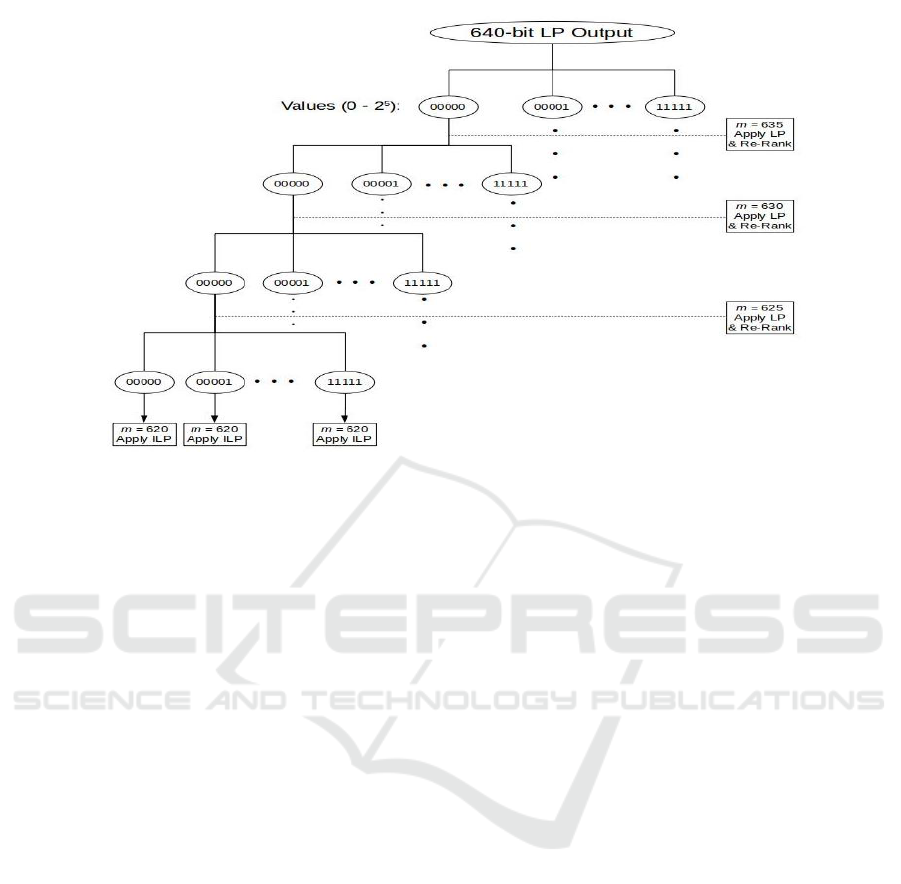
Figure 4: Removing 20 bits in u
u
u
T
in blocks of size 5.
(rows) with u
10
= 1. Because the value of u
10
in the
LP output is 0.9, this column will have a preponder-
ance of high values (closer to 1), so removal of this bit
will shrink the solution space but much less so com-
pared to that caused by removal of a bit in the right-
most section of the table. As an example of the latter,
the LP output of u
640
is 0.52, so the high values (close
to 1) and low values (close to 0) would tend to balance
out. In the computation of the average, there would
be fewer values with 1, so creating a sub-instance by
removing this bit would shrink the space to a much
larger extent. In general, removing multiple bits at
the rightmost end would considerably reduce the so-
lution space vis-a-vis removing bits from the left of
the vector. This explains why the success rate for re-
moval of bits from Regime H is so much higher than
that from regime L (Table 1).
In Figure 2 the unique binary solution is high-
lighted. Finally, the LP value of u
147
is 0.19, so our
prediction is that its value is 0. However, its actual
value is 1. If a sub-instance could be created by first
correcting and then removing this bit, we would ex-
pect the solution space to greatly shrink. Removing
such bits, especially in Regime L, appears to be an
attractive option but identifying them is non-trivial.
4.2 Instance Classification and
Optimization
Our estimates of execution time to obtain the secret,
u
u
u
T
, vary greatly across instances. One metric to clas-
sify instances is the number of mis-predicted values
in u
u
u
T
. However, this requires knowledge of u
u
u
T
. With
knowledge of only A
A
A and b
b
b, is it possible to deduce the
class affiliation of an instance? (Class A contains the
weak/easy instances and Class C contains the hard-
est).
For a given instance, we count the number of val-
ues in the output of the LP solver within specified
ranges. Figure 3 shows the count of the values greater
than 0.95 or less than 0.05. Also included for compar-
ison are the counts of values greater than 0.85 or less
than 0.15. The instances (along the X axis) are ar-
ranged in decreasing order of the number of correct
predictions. These metrics appear to be consistent
and could be used as a basis for instance classification
(Figure 3). As supporting evidence for the validity of
this classification scheme, we note that the successful
instances reported in Tables 1 and 2 are overwhelm-
ingly in Class A.
In our experiments on removing r bits in Regime
H, we created sub-instances of size m − r bits by re-
moving all r bits in one go. Another option is to create
sub-instances of decreasing sizes, m − b, m − 2b, . . . ,
m − r, with b, the block size, as selectable parameter.
As before, the LP solver would be initially applied on
the given instance but now b rightmost bits (in Regime
H) would be removed to create 2
b
sub-instances of
size m − b, one per combination of values of the b
bits (Figure 4). The LP solver would be applied to
each sub-instance and the LP output sorted anew in
increasing order of proximity to 0.5. The rightmost
b bits (in Regime H) would be removed to create in-
stances of size m − 2b and so on. Only after all r bits
SECRYPT 2018 - International Conference on Security and Cryptography
564

were removed would ILP be applied on the resulting
sub-instances.
A key feature of this approach is that LP is used
repeatedly and the bits to be removed are dynami-
cally determined by subsequent applications of LP.
This leads to a greater shrinkage of the solution space.
As proof of concept, we considered the removal of 50
rightmost bits in Regime H in two steps - removal of
30 bits first followed by the removal of 20 bits. The
success probability increased from 20% for a one-shot
removal to 26% in the 2-step case. In the 5-step case
(removal of 10 + 10 + 10 + 10 + 10 bits), the success
probability increased to 32%. In the case of removal
of just 20 bits in Regime H, the success probability
increased by 20% for a 4-step removal (5 + 5 + 5 + 5
bits) over a single step removal.
One possible advantage of multi-step removal is
that it may be likely to prune the search tree in Figure
4. For example, it may be possible to rank the dif-
ferent sub-instances based on presumed probability
of success heuristically computed from the LP out-
puts. Root-to-leaf paths deemed to have greater suc-
cess probability could be explored first resulting in
much reduced execution time.
5 CONCLUSION
We addressed the challenge posed by (Galbraith,
2013) to obtain the plaintext in a ciphertext only at-
tack for m = 640. We were able to solve the challenge
for 5 instances out of 1000 (in 1 day with 150 cores)
and for 10 instances (in 2 days with 2400 cores). We
applied LP/ILP on reduced instances by removing bits
in different regimes - L, M and H. We found that it
was most effective to remove bits in H. A sub-instance
of size 550 can be solved with 97% success proba-
bility by removing just 90 bits in H. We performed
an optimization wherein we removed bits in smaller
blocks rather than in one go and obtained significant
improvement in success rate. While our initial re-
sults are based on experiments with 1000 random in-
stances, we generated and tested another 1000 ran-
dom instances and our conclusions are nearly identi-
cal. Finally, we outlined a very simple way to catego-
rize instances into classes A, B and C where instances
in A are easiest to solve while instances in C are hard-
est.
The approach and experiments reported here,
while simple, were partially successful in trying to
address Galbraith’s challenge. Through insightful re-
finements and optimizations, we feel it may be possi-
ble to greatly increase the success rate while decreas-
ing the execution time.
REFERENCES
Agrawal, S., Boneh, D., and Boyen, X. (2010). Lattice basis
delegation in fixed dimension and shorter-ciphertext
hierarchical IBE. In Annual Cryptology Conference,
pages 98–115. Springer.
Bai, S. and Galbraith, S. D. (2014). Lattice decoding at-
tacks on binary LWE. In Australasian Conference
on Information Security and Privacy, pages 322–337.
Springer.
Brakerski, Z., Gentry, C., and Vaikuntanathan, V. (2014).
(leveled) fully homomorphic encryption without boot-
strapping. ACM Transactions on Computation Theory
(TOCT), 6(3):13.
Brakerski, Z. and Vaikuntanathan, V. (2014). Efficient
fully homomorphic encryption from (standard) LWE.
SIAM Journal on Computing, 43(2):831–871.
Cash, D., Hofheinz, D., Kiltz, E., and Peikert, C. (2010).
Bonsai trees, or how to delegate a lattice basis. In An-
nual International Conference on the Theory and Ap-
plications of Cryptographic Techniques, pages 523–
552. Springer.
Coron, J.-S., Naccache, D., and Tibouchi, M. (2012). Pub-
lic key compression and modulus switching for fully
homomorphic encryption over the integers. In Annual
International Conference on the Theory and Applica-
tions of Cryptographic Techniques, pages 446–464.
Springer.
Galbraith, S. D. (2013). Space-efficient variants
of cryptosystems based on learning with er-
rors. url: https://www. math. auckland. ac. nz/˜
sgal018/compact-LWE. pdf.
Herold, G. and May, A. (2017). LP solutions of vecto-
rial integer subset sums–cryptanalysis of galbraiths bi-
nary matrix LWE. In IACR International Workshop on
Public Key Cryptography, pages 3–15. Springer.
Lindner, R. and Peikert, C. (2011). Better key sizes (and
attacks) for LWE-based encryption. In Cryptogra-
phers Track at the RSA Conference, pages 319–339.
Springer.
Lyubashevsky, V., Peikert, C., and Regev, O. (2010). On
ideal lattices and learning with errors over rings. In
Annual International Conference on the Theory and
Applications of Cryptographic Techniques, pages 1–
23. Springer.
Micciancio, D. and Peikert, C. (2013). Hardness of SIS
and LWE with small parameters. In Advances in
Cryptology–CRYPTO 2013, pages 21–39. Springer.
Peikert, C., Vaikuntanathan, V., and Waters, B. (2008).
A framework for efficient and composable oblivious
transfer. In Annual International Cryptology Confer-
ence, pages 554–571. Springer.
Regev, O. (2005). On lattices, learning with errors, ran-
dom linear codes, and cryptography. In Proceedings of
the 37th Annual ACM Symposium on Theory of Com-
puting, Baltimore, MD, USA, May 22-24, 2005, pages
84–93.
Learning Plaintext in Galbraith’s LWE Cryptosystem
565
