
A Comparative Study of PID-PSO and Fuzzy Controller for Path
Tracking Control of Autonomous Ground Vehicles
Sami Allou and Youcef Zennir
Automatic Laboratory of Skikda, Université 20 août 1955 Skikda, Skikda, Algeria
Keywords: Mobile Robot, Particles Swarm Optimization, PID Controller, Fuzzy Controller, Kinematic Vehicles Model,
Trajectory Tracking, V-Rep 3D Simulation.
Abstract: The work presented in this paper focuses on platonning navigation control (train of vehicles) according to
different trajectories. As a first step we based our study on two vehicles. an kinematic model of the two
vehicles is described followed by a PID multi-controller control approach based on conventional PID, PID
optimized by Particle Swarm Optimization (PSO) technique and fuzzy controller applied to the longitudinal
and lateral control of each vehicle. Controller parameters optimization is based on a fitness function time
weight square error (ITSE). The communication between the two vehicles is ensured with the exchange of
information, the speed and orientation angle, respecting the safety distance between the vehicles. To
approve our approach we have use different reference trajectory in different simulations in matlab-simulink
environment and v-rep 3D simulation. The simulation obtained results illustrate the efficiency of our control
design and open the perspectives for future work.
1 INTRODUCTION
Today's transportation systems are increasingly
complex systems with some difficulty in ensuring
the control and security of these systems the number
of vehicles is growing exponentially and the
accomplishment of simple tasks really becomes a
defeat with risk for the human being autonomous
vehicles can solve this problem and act in the place
of human beings. greasy to their capacity mobile
robots (Car like vehicles or autonomous vehicles)
are able to perform many tasks in dangerous places
where humans cannot enter, those sites where
harmful gases or high temperature are present in a
harsh environment to humans and to ensure the
delivery of goods at long distances in risky roads
with autonomous vehicles we can save money by
performing various routine tasks (Baturone et al.,
2004). So that this goal is to ensure this means that it
is necessary to upgrade and optimize autonomous
vehicle controllers that solve complicated problems
and tackle complicated in variable environments. in
the literature different control approach are used to
control the navigation of autonomous vehicles like
fuzzy controller, controller based on networks of
noodles, sliding mode control (Garcia et al., 2008;
Bingyi et al., 2017; Fernandes, 2010). The simplest
controller used in controlling the navigation of an
autonomous vehicle being the PID controller. The
traditional PID controller has been used to control
the various industrial processes in the world (Bingyi
et al., 2017). This controller has a major problem
with a fixed choice of these parameters in a
dynamic, complex environment and when there are
variations in the installation parameters and
operating conditions, which may cause the controller
to not provide the parameters control performance
required. There are different methods for adjusting
the PID controller parameters according to the
variation in the state of the environment and the
system among these best-known methods, frequently
used in industrial applications, the Ziegler-Nichols
method, the genetic algorithm GA, fuzzy logic
controller (Cao and Liu, 2017), etc. the PSO
optimization technique was another very fashionable
method of tuning. this technique (PSO) introduced
by Kennedy and Eberhart (Campolo et al., 2015;
Ploeg et al., 2014) is one of the modern heuristic
algorithms, it was motivated by the behavior of
organisms, such as fish farming and flocking of
birds (Cao and Liu, 2017). Other modern heuristics
algorithms are used as reinforcement learning (Q-
learning) to optimize the parameters of the PID
296
Allou, S. and Zennir, Y.
A Comparative Study of PID-PSO and Fuzzy Controller for Path Tracking Control of Autonomous Ground Vehicles.
DOI: 10.5220/0006910902960304
In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 1, pages 296-304
ISBN: 978-989-758-321-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
controllers. Unlike other heuristics (Campolo et al.,
2015), PSO has a flexible and well-balanced
mechanism to improve global and local exploration
capabilities (Ploeg et al., 2014; Dumont, 2006;
Bouibed, 2010). This technique is easy to implement
and informally efficient. In this paper, a new control
approach based on multi-PID-PSO controllers to
optimally design a PID controller for tracking the
trajectory of an autonomous vehicles train
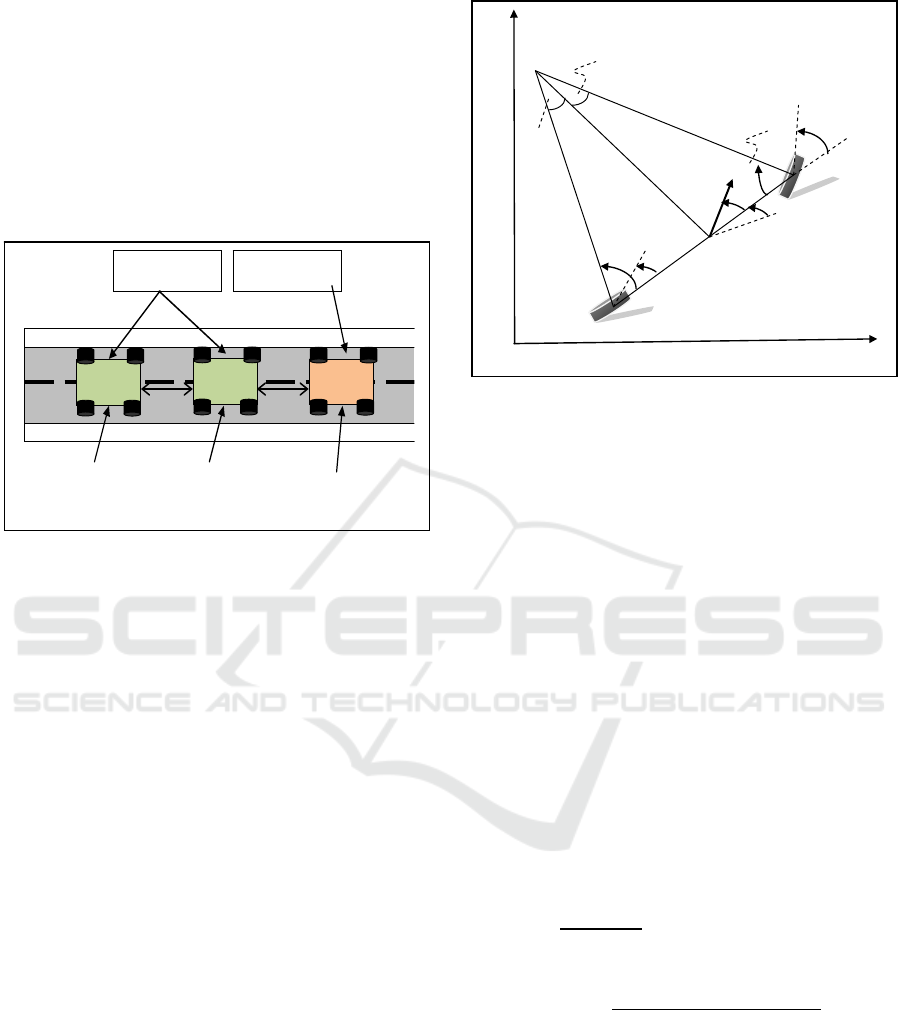
(platonning) is proposed (figure 1).
Figure 1: Architecture of Platonning system.
This article was organized as follows: in section
2, a kinematic model of the autonomous vehicle
(mobile robot) is described. In Section 3, the method
of optimizing the particle swarm is reviewed.
Section 4 describes how PSO is used to design the
PID controller optimally for the mobile robot to
control the speed and angle of orientation of the
vehicle. Section 5 simulation and results.
2 KINEMATIC MODLING
Different model of autonomous electrical vehicles
existing in the literature (Baturone et al., 2014). this
model more and less complex depend of the
situation and the elements composed the vehicle.
The model is more represent the vehicle when its
take into account all the forces applied on the
system. in this case the control results obtained are
high efficient. Our work is based on the control
study of two autonomous electric vehicles, that used
four wheels driven by DC motor, the braking is done
by electromagnetic brakes when the absence of
current it also has dual front steering system and
back. The simplified geometric model of vehicles is
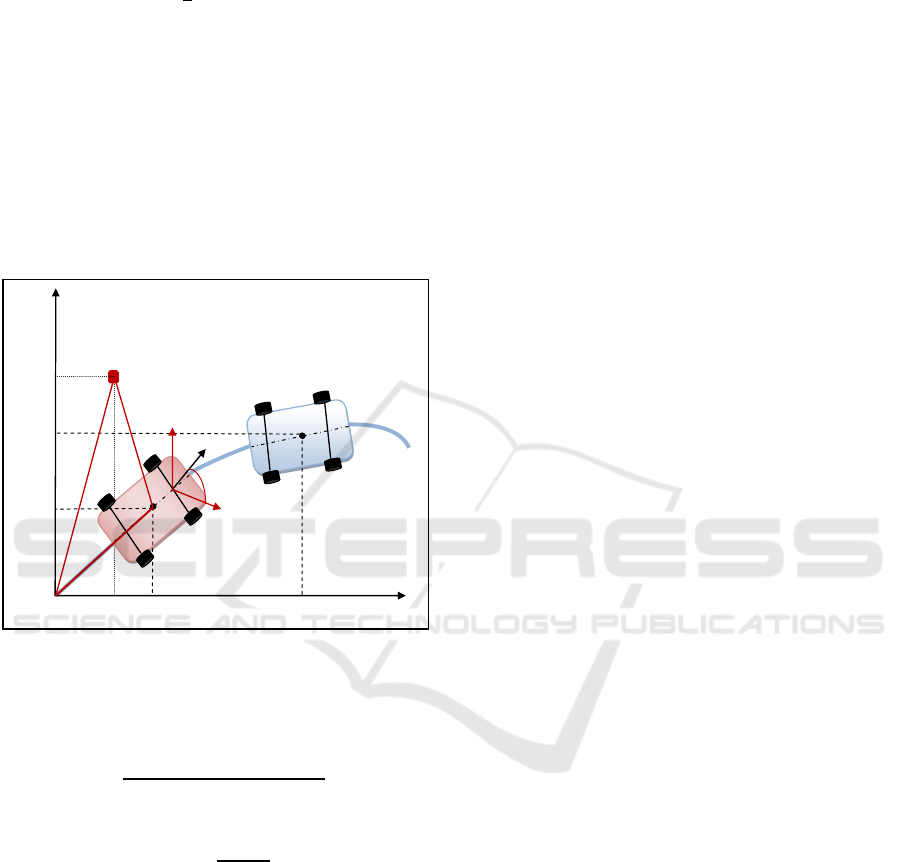
represented by the following figure :
Figure 2: Geometric model of Electric vehicle (RobuCar)
and kinematic model.
With :
O : is the instantaneous rolling centre for the vehicle
C : gravity centre of vehicle.
β : slip angle of the vehicle
Ψ : heading angle of the vehicle.
δf,δr : steering angles.
lr, lf :distance between gravity centre of vehicle and
the wheels (AC and BC)
R : the radius (OC)
The course angle for the vehicle is γ=β+Ψ . Apply
the sine rule to triangle OCA with same
simplification, the kinematic model is described by
the following formulary :
=∙cos
(
+
)
(1)
=∙sin
(
+
)
(2)
=
∙cos
(
)
+
∙tan
−tan
(
)
(3)
=
∙tan
+
∙tan
(
)
+
(4)
In this model there are three inputs:δ
, δ
and V.
In our work we consider that our vehicle has a
simple braking and the slip angle equal zero (β=0
and δr=0). The kinematic model in this situation is
as follows :
=∙cos
(
)
(5)
PID-PSO controller Controlled by Man
d
v
1
,Ψ
1
v
2
,Ψ
2
d
vehicle
1
(
V1
)
vehicle
2
(V2)
vehicle
3
(
V3
)
v
3
,Ψ
3
A
C
B
O
δ
f
δ
r
Ψ
β
V
π/2+δ
r
π/2-δ
f
δ
f
-
β
β
-
δ
r
R
l
r
l
f
x
y
A Comparative Study of PID-PSO and Fuzzy Controller for Path Tracking Control of Autonomous Ground Vehicles
297
=∙sin
(
)
(6)
=
∙tan
(7)
With : L=
+
To keep the mobile robot on our desired
trajectory it is necessary to design a regulator which
will allow tracking of arbitrary trajectories (xr (t), yr
(t)). The design of controller which we used is based
on conventional PID controller it receives the values
of distance and the robot location relative to the path
as shown in Fig 3,
Figure 3: Technical diagram of the technique.
The error victor represents the distance between
the vehicle and the desired position.
=
(
x
−x
)
+
(
y
−
y
)
(8)
Ψ
=tan
y
−
y
x
−x
(9)
=
−
(10)
This model is used for the two vehicles. we
described the architecture of multi-controller PID-
PSO control approach in the following section.
3 PARTICLE SWARM
OPTIMIZATION WITH PID
The Particle Swarm Optimization (PSO) is
evolutionary computational technique based on the
movement and intelligence of swarms looking for
the most fertile feeding location; it was developed in
1995 by James Kennedy and Russell Eberhart. PSO
is one of the optimization techniques and a kind of
evolutionary computation technique. This algorithm
is simple, easy to implement and few parameters to
adjust mainly the velocity. It’s inspired by social
behavior of birds and fishes and it's combines self-
experience with social experience and applies to
concept of social interaction to problem solving (Al-
Mayyahi, 2015) (Turki and Abdulkareem, 2012).
The goal of Optimization is to find values of the
variables that minimize or maximize the objective
function while satisfying the constraints. The
optimization needs the good mathematical model of
the optimization problem and an algorithm that
should have robustness (good performance for a
wide class of problems), efficiency (not too much
computer time) and accuracy (can identify the error).
The optimization is based in population; it has been
applied successfully to a wide variety of search and
optimization problems. In this technique, a swarm of
n individuals communicate either directly or
indirectly with one another search directions
(gradients) (Al-Mayyahi, 2014). PSO technique is
not only a tool for optimization, but also a tool for
representing socio cognition of human and artificial
agents, based on principles of social psychology. A
PSO system combines local search methods with
global search methods, attempting to balance
exploration and exploitation (Zoleikha et al., 2017).
The Population-based search procedure in which
individuals called particles change their position
(state) with time. The Particles fly around in a
multidimensional search space. During flight, each
particle adjusts its position according to its own
experience, and according to the experience of a
neighboring particle, making use of the best position
encountered by itself and its neighbor. Suppose that
the search space is D-dimensional, then the ith
particle of the swarm can be represented by a D-
dimensional vector X
=[x
x
…x
]
. The
velocity of the particle can be represented by another
D-dimensional vector V
=[Vi
(
1
)
Vi(2)…Vi(D)]
.
The best previously visited position of the ith
particle is denoted as P
=[p
p
…p
]
. Defining
‘‘g’’ as the index of the best particle in the swarm,
where the gth particle is the best, and let the
y
x
G2
xx
d
o
y
G2
y
G1
y
d
P
m
d
x
G1
Ψ
the desired point
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
298
superscripts denote the iteration number, then the
swarm is manipulated according to the following
two equations (Zennir et al., 2017).
(
+1
)
=.
(
)
+
.
(
)
−
(
)
+
.
(
)
−
(
)
(11)
(
+1
)
=
(
+1
)
+
(
)
(12)
where t = 1, 2, . . . , D; i= 1, 2, . . . , M, and M is
the size of the swarm (i.e. number of particles in the
swarm); c1, c2 are the positive values, called
acceleration constants; r1,r2 are the random
numbers uniformly distributed in [0, 1]. Typically
w(t) is reduced linearly, from w
to w
, each
iteration, a good starting point is to set w
to0.9
and w
to0.4.
w
(
t
)
=
(
)
×(
)
+w
(13)
Thought V
has been found not to be
necessary in the PSO with inertia version, however it
can be useful and is suggested that a V
=X
be used. The original procedure for implementing
PSO is as (Allou et al., 2017). In PID controller
design methods, the most common performance
criteria are integrated absolute error (IAE), the
integrated of time weight square error (ITSE),
integrated of squared error (ISE) and Mean Square
Error (MSE) (Al-Mayyahi et al.,2015). In this work
we use parallel PID, and the coefficients Kp, Ki, Kd
are determined by the PSO algorithm using ITSE
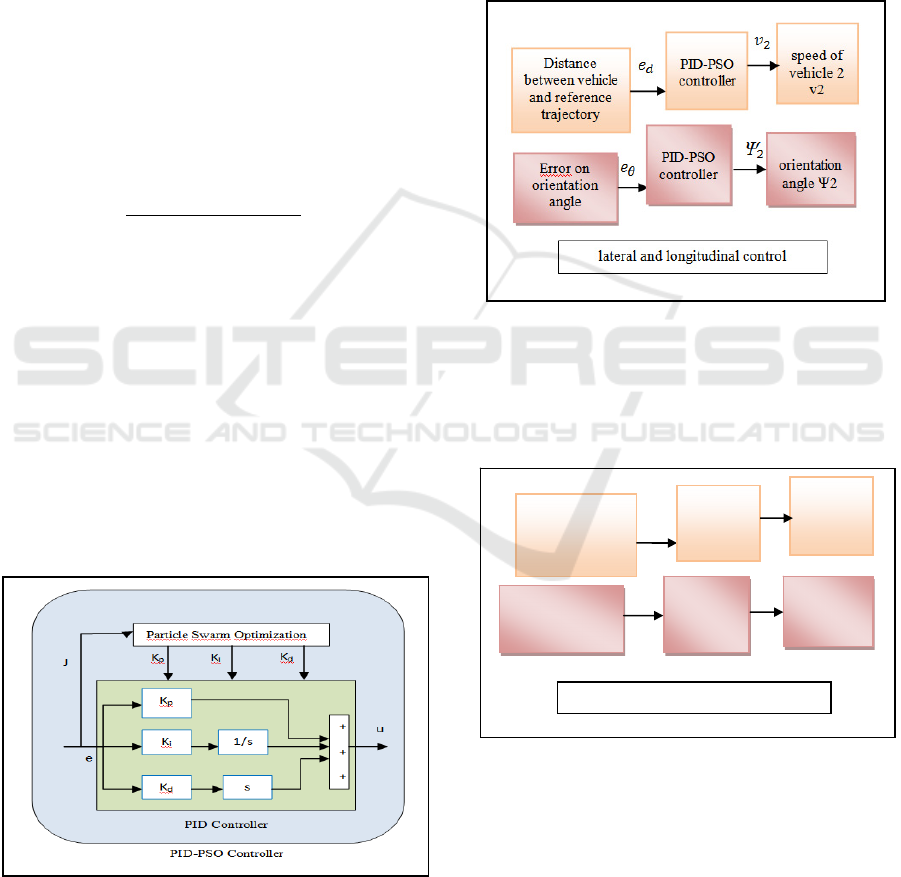
performance criteria (figure 4).
Figure 4: PID parameters based on PSO.
With: J: ITSE performance criteria (fitness
function); u: law control; e: error.
4 DESIGN OF CONTROLLERS
In this paper we used two type of controller. in the
first two PSO algorithm to find the optimal
parameters for two PID controllers for the control of
velocity and angle of orientation of vehicles. Figure
5 shows the block diagram of optimal PID controller
for the vehicles. The design of our control approach
used to control lateral and longitudinal position of
vehicles is shown in the following figure:
Figure 5: Optimal PID-PSO control structure.
The second controller based fuzzy controller
applied in lateral and longitudinal control like in
following figure:
Figure 6: Control structure with Fuzzy controller.
The architecture of control for the controllers in
simulink is illustrted in the following figures:
lateral and longitudinal control
2
Distance between
vehicle and
reference
trajectory
Fuzzy
controller
speed of
vehicle 2
v2
Error on
orientation angle
Fuzzy
controller
Ψ
orientation
angle
Ψ
2
Ψ
2
A Comparative Study of PID-PSO and Fuzzy Controller for Path Tracking Control of Autonomous Ground Vehicles
299
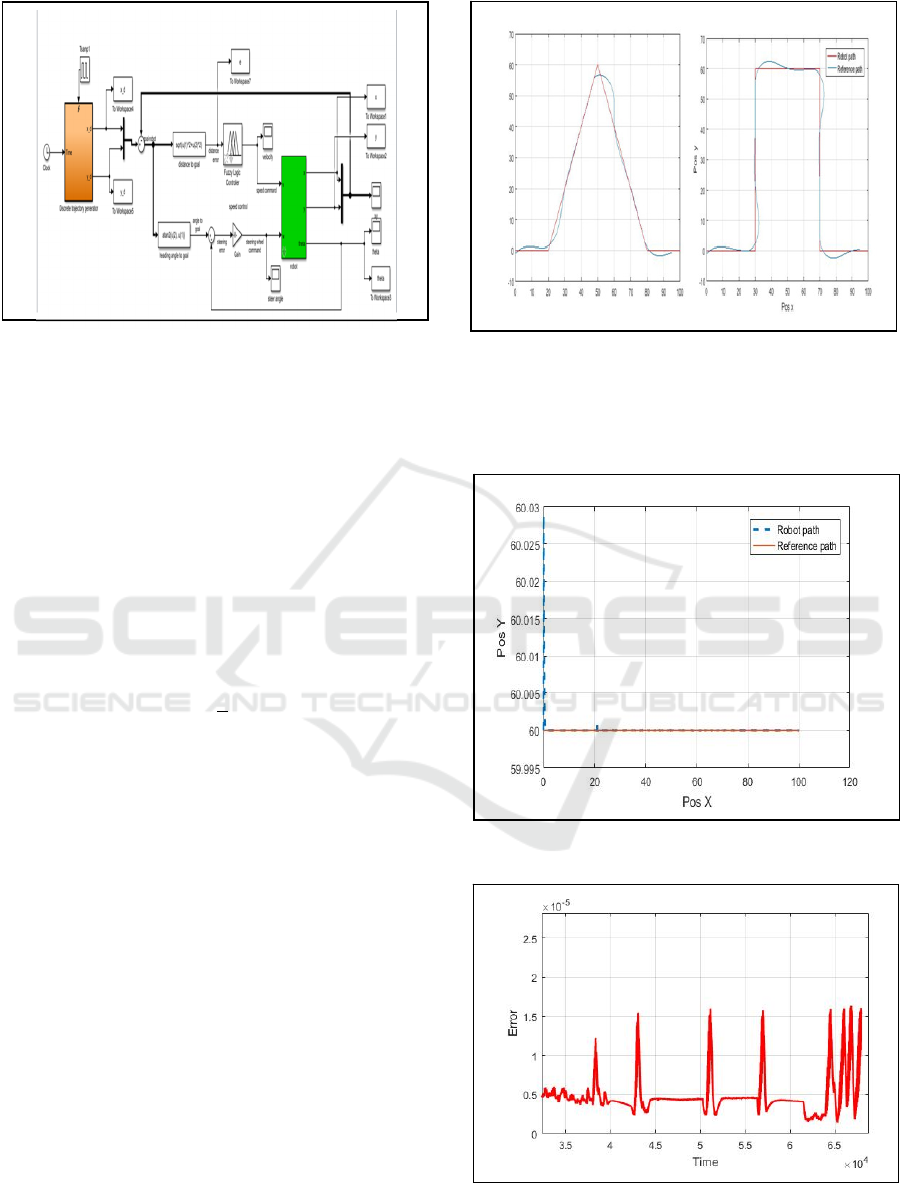
Figure 7: Control block diagram with fuzzy controller.
The Parallel PID controller parameters are
extracted using the PID tool command. The
following figure shows that our system is regulated
by a parallel PID controller. We control the speed
and orientation angle of vehicle. The transfer
function of PID controller used to control orientation
angle is as follows:
=∗
(14)
The transfer function of PID controller used to
control speed of vehicle is as follows:
G
(
s
)
=Kp+Ki.
1
s
+Kd.s∙e
(15)
5 SIMULATION
We have simulated our architecture control approach
in continues time. The simulation aim is to approve
the controller's efficiency on two types of controller
(PID and PID-PSO controller) in five different
trajectory in plan (triangle, rectangle, sinusoidal
form, straight line form and trapezoidal form). The
parameter of PID controller are:
- Controller for speed
=25;
=0.1;
=0.02
- Controller for orientation angle
=100
The obtained results without control are
illustrated in the following figures:
Figure 8: Rectangle and triangle trajectory without control.
The obtained results are illustrated in the
following figures:
Figure 9: Straight line trajectory with PID-PSO.
Figure 10: Error with straight line trajectory (PID-PSO
controller).
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
300
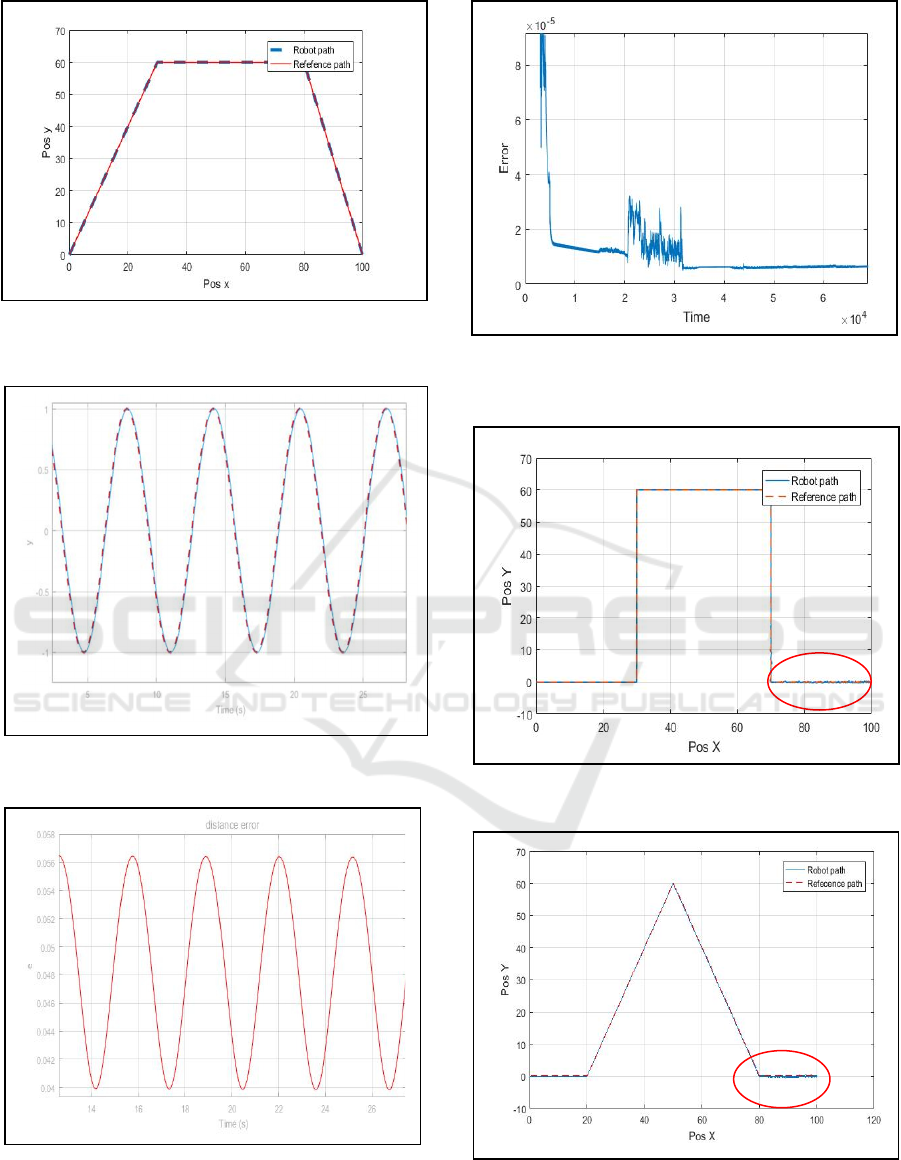
Figure 11: Trapezoidal trajectory with PID-PSO
controller.
Figure 12: Sinusoidal trajectory with PID-PSO controller.
Figure 13: error with Sinusoidal trajectory (PID-PSO).
Figure 14: Error with rectangle trajectory PID-PSO
controller.
Figure 15: Rectangle trajectory with PID-PSO controller.
Figure 16: Curved triangle trajectory with PID-PSO
controller.
A Comparative Study of PID-PSO and Fuzzy Controller for Path Tracking Control of Autonomous Ground Vehicles
301

Figure 17: Error with triangle trajectory with PID-PSO
controller.
Figure 18: Error with rectangle trajectory with PID-PSO
controller.
The obtained results obtained with fuzzy
controller in different trajectory are illustrated in the
following figures:
Figure 19: Rectangle trajectory with fuzzy controller.
Figure 20: Triangle trajectory with fuzzy controller.
Figure 21: Trapezoidal trajectory with fuzzy controller.
Table 1: Error obtained with pid controller and fuzzy
controller.
Trajectory Error with
PID
controller
Error with
Fuzzy
controller
Triangle form 0.033-0.039 0.014-
0.0175
Rectangle form 0.0315 0.0139
Sinusoidal form 0.015 0.007
Curved form 0.0095-0.0195 0.003-0.006
Trapezoidal form 0.03391 0.01395
Straight form 0.034 0.0137
The figures figure.8 show the tracking of the
trajectory without optimization of PID controller.
After adjusting the parameters of the controllers
(PID) with PSO technique, the results are much
improved and the tracking error is very small for all
type of trajectory (figure.9-figure.18). But we have
observed too that same error in the end of triangle or
rectangle trajectory (figure.19 and figure.20). The
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
302

tracking error with sinusoidal trajectory must be
improved (figure. 13). The figures figure.19,
figure.20 and figure.21 shows the tracking of the
trajectory after adjusting the parameters of the
controllers (PID and Fuzzy) the results are much
improved and specially with the fuzzy controller as
shown in the error table (table.I). This efficiency of
the fuzzy controller is whatever the type of trajectory
and specially in curved and sinusoidal trajectory.
With obtained results we can observed that Fuzzy
controller give very important stability and precision
in the end of trajectory compared with PID and PID-
PSO controllers. PSO-PID controller give high
precision in all type of trajectory only in curved and
sinusoidal trajectory. 3D simulation in v-rep in the
following figure:
Figure 22: 3D simulation in v-rep with two vehicles.
6 CONCLUSION
In this paper we have proposed A comparative study
with different controller design PID, PID-PSO and
Fuzzy controller applied to control path tracking for
platonning autonomous vehicles with four wheels.
The controllers choses for able to offer more tracking
flexibility and stability of our system. Different
simulation has been realized in different trajectory
with very interesting results in lateral and
longitudinal control of vehicles with Fuzzy controller
and PID-PSO controller. We can conclude that our
approach of control gives high results in stability and
precision but this approach must be more optimized
where the platonning vehicles travel in curved
trajectory and in the end of trajectory for PID-PSO
controller. In the future works we plan, to improve
our control approach with other optimization
algorithm like Fractional PID controller (FOPID)
optimizing by PSO algorithm, Genetic Algorithm
and wolf Algorithm to optimize the parameters of
controller in other trajectory with obstacle.
REFERENCES
Baturone, I. Moreno-Velo, Sánches-Solano, F. J. S. and
Ollero, A., 2004. “Automatic Design of Fuzzy
Controllers for Car-Like Autonomous Robots”. IEEE
Transactions on fuzzy systems, vol.12, n°.4, pp.....
García, C. Strang, T. Lehner, A., 2008. “A Broadcast
Vehicle to Vehicle Communication System in Railway
Environments“, ISVCS 2008, July 22 - 24, 2008,
Dublin, Ireland, pp.6.
Bingyi, L. Dongyao, Kejie, J. Dong, L. N. Jianping, W.
and Libing, W., 2017.“A Joint Control-
Communication Design for Reliable Vehicle
Platooning in Hybrid Traffic“. IEEE Transactions on
Vehicular Technology, 66 (10). pp. 9394-9409.
Fernandes, P., 2010. "Platooning of Autonomous Vehicles
with Intervehicle Communications in SUMO Traffic
Simulator". 13th IEEE International Conference on
Intelligent Transportation Systems, Portugal,
September, 19-22, 2010, pp.1313-1318.
Cao Y. and liu, S., 2017, “Visual Servo Control for
wheeled robot platooning based on homography”. 6th
Data Diven Controol and Lerning System, pp. 628 -
632.
Campolo, C. Mlinaro, A. Araniti G. and Berthet, A. O.,
2017. “Better Platooning Control Toward
Autonomous Driving: An LTE Device to- Device
Communication Thate Meets Ultralow Latency
Requirements”, IEE vehicular Technology Magazine.
Vol 12, Issue 1, pp.30-38.
Ploeg, J. Vande WOuw, N. and Nijmeijer, H., 2014.“Lp
String Stability of Cascaded systems/ Application to
vehicle Platooning”, IEE Trans. On Control Syst.
Technologe, vol 22, No 2, pp.786-793.
Dumont, P-E., 2006. “Tolérance active aux fautes des
systèmes d’instrumentation“, Thèse doctorat,
université Lille 1, p.163.
Bouibed, K., 2010. “Contribution à la gestion de
défaillances d’un train de véhicules électriques légers
autonomes “, Thèse doctorat, université Lille 1, p.181.
Al-Mayyahi, A., 2015. “Path Tracking of Autonomous
Ground Vehicle Based on Fractional Order PID
Controller Optimized by PSO“, IEEE 13th
International Symposium on Applied Machine
Intelligence and Informatics, January 22-24, Slovakia,
pp.109-114.
Turki, Y. A. Abdulkareem, A. A., 2012. "PSO-based
Optimum Design of PID Controller for Mobile Robot
Trajectory Tracking ", International Journal of
Computer Applications, vol.47, no.23, pp.30-35.
Al-Mayyahi, A. Wang, W. and Birch, P., 2015."Design of
Fractional-Order Controller for Trajectory Tracking
Control of a Non-holonomic Autonomous Ground
Vehicle", International Journal of Control Autom
Electr Syst, p.14
A Comparative Study of PID-PSO and Fuzzy Controller for Path Tracking Control of Autonomous Ground Vehicles
303

Al-Mayyahi, A. Wang, W. and Birch, P., 2014. "Adaptive
Neuro-Fuzzy Technique for Autonomous Ground
Vehicle Navigation", Robotics, pp.349-370.
Zoleikha, A.B Satadru, D. and Pisu, P., 2017." Real-time
Detection and Estimation of Denial of Service Attack
in Connected Vehicle Systems", Ieee Transactions On
Intelligent Transportation Systems, Vol. Xx, No. X,
p.11.
Allou, S. Zennir, Y. and Belmeguenai , A., 2017 " Fuzzy
logic controller for autonomous vehicle path tracking",
18
th
international conference on Sciences and
Techniques of Automatic control & computer
engineering - STA'2017, Monastir, Tunisia, December
21-23, pp.328-333.
Zennir, Y., Mechhoud, E-A., Seboui, A., Bendib, R.,
2017." Multi-controller approach with PSO- PIλDμ
Controllers for a Robotic Wrist". The 5
th
International
Conference on Electrical Engineering – Boumerdes
(ICEE-B), October 29-31, Boumerdes, Algeria, p.7.
ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics
304
