Initial Tuning Procedure for Attitude and Vertical Movement Controllers

in Multirotor Aerial Vehicles with Heterogeneous Propulsion Units

Przemysław Ga¸sior, Adam Bondyra and Stanisław Gardecki

Institute of Control, Robotics and Information Engineering,

Poznan University of Technology, Piotrowo 3A, Poznan, Poland

Keywords:

Multirotor UAV, PID Control, Tuning, Propulsion Units, Modelling.

Abstract:

In this paper, a hybrid procedure of tuning the control structure of a newly developed multirotor aerial platform

is presented. Such situation presents a demanding task because there are no initial parameters of PID control-

lers ensuring safe ﬂight conditions. Most methods base on full mathematical models which can be divergent

from the real plant and require a process of detailed system’s identiﬁcation. The second area of solutions

utilises different types of test benches to perform trial and error tuning in safe conditions. A method presented

in this article comprises a hybrid approach connecting both practices. The key element in this solution is a

model of the implemented propulsion system and physical parameters of the airframe itself obtained from the

CAD software. System noise variances are gathered from experiments on the test bench and implemented

in appropriate simulations. Next, the optimisation can be executed to gather parameters for every constituent

controller. Finally, veriﬁcation in real conditions is performed. The presented method was used for the de-

velopment of two signiﬁcantly different multirotor UAVs during the pre-ﬂight PID control tuning phase. An

approach is versatile for both symmetrical and unsymmetrical heterogeneous airframes.

1 INTRODUCTION

Over the past decade, micro multirotor aerial vehicles

became very popular in research and commercial ap-

plications, mostly because of their ﬂight characteris-

tics. New solutions concerning propulsion systems

and airframe designs are developed constantly. Al-

ong with increasing complexity and demands of UAV

applications, more sophisticated aerial platforms with

plenty of the on-board equipment are introduced. Ho-

wever, more payload requires extended lift capability,

which is usually achieved by increasing power and

size of propulsion units. Unfortunately, a signiﬁcant

rise of the UAV mechanical outline prevents ﬂights

in closed or indoor spaces. An exemplary solution

for this problem is the introduction of coaxial propul-

sion into the micro UAV technology, which increases

maximum thrust and payload lift capabilities within

the same physical size (Bondyra et al., 2016). For

some designs, the process of optimising the payload

capabilities and ﬂight time efﬁciency leads to usage of

heterogeneous, non-symmetrical propulsion systems.

Example of such structure is the Kruk UAV described

further in this paper.

While there is a great ﬂexibility in designing and

arranging motors and propellers for particular UAV

design, every divergence from classic, symmetrical

quarto-/hexa-/octo- copter scheme results in the more

demanding control strategy. There are several, well

researched approaches to control of a multirotor aerial

platform: attitude, attitude with altitude hold and po-

sition control. Different ﬂight controllers, especially

the custom ones, are equipped with various control

algorithms, starting from attitude ((Bouabdallah and

Siegwart, 2007), (Dikmen et al., 2009)), vertical mo-

vement ((Ga¸sior et al., 2016a), (Connor et al., 2017))

or overall position ((Gasior et al., 2017)). However, in

every case of the newly developed UAV, the problem

of initial tuning of its controllers arise. This essen-

tial for the proper in-ﬂight operation of the UAV task

has to be performed in a very cautious way in order to

reduce risk to the operator or equipment.

In addition, ﬂexible and universal tuning proce-

dure is very useful for the further exploitation of the

UAV, i.e. during signiﬁcant payload rearrangement,

development of different control methods or adapta-

tion to varying ﬂight conditions.

G ˛asior, P., Bondyra, A. and Gardecki, S.

Initial Tuning Procedure for Attitude and Vertical Movement Controllers in Multirotor Aerial Vehicles with Heterogeneous Propulsion Units.

DOI: 10.5220/0006911304650472

In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 2, pages 465-472

ISBN: 978-989-758-321-6

465

2 RELATED WORK

In general, there are three methods of initial tuning of

controllers for multirotor aerial platforms. The ﬁrst

solution is based on the expert knowledge of the team

of engineers and parameters obtained during develop-

ment of previously constructed vehicles. If there are

no major differences in the airframe design and pro-

pulsion setup, there is a high probability that a new

design will require only some minor, in-ﬂight tuning.

This is a situation very common in development pro-

jects, where new iterations of market products are re-

leased. However, there may be differences not only

in physical parameters and performance but in me-

chanical vibrations due to use of different materials

and speciﬁc aspects of structural design. It is a well-

known issue leading to errors and inadequacies in the

state estimation which automatically leads to failure

in the control process. To sum up, even in this ap-

proach it is recommended to test platform in the test

stand before carrying out free ﬂight experiments.

The second method depends on the complete mat-

hematical model of the developed platform. Unfortu-

nately, it is hard to utilise such model for newly con-

structed UAV, while there is no data to tune the mo-

del itself. Sometimes the sub-models are used to sim-

plify this process. In such case, the problem is divi-

ded into several simpler simulations, i.e. concerning

single axis of rotation. In addition, noise in sensor re-

adings has a great impact on control quality as well.

Therefore, there is a requirement to perform noise le-

vels trimming.

Third approach utilises various test benches ((Pa-

nizza et al., 2016), (Bondyra et al., 2017), (Hoffmann

et al., 2010), (Tayebi and McGilvray, 2006)), which

allow performing tuning process in safe, laboratory

conditions without the risk of damaging the equip-

ment in-ﬂight. In addition, this method is based on

the trial and error technique. Without reaching into

the details of mathematical modelling, parameters are

chosen on the basis of rules corresponding to the type

of the applied control technique. This process can

also be automated which leads to the reduction of

tuning time (Wang and Poksawat, 2017) (Howard,

2017). It has to be mentioned, that platform during

the tuning process on the test bench can change its

physical characteristics, since ﬁxing the UAV in test

rig inﬂuences mainly the vibration levels in compari-

son to the in-ﬂight performance. Test bench usually

dampens vibrations due to the dispersion in extended

mechanical structure. Therefore, during the real ﬂight

tests, noise amplitude can be signiﬁcantly higher, dis-

turbing state estimation and ﬂight control. Another

important issue with ﬁxing the UAV to the stationary

bench is the introduction of friction in axes of rota-

tion. Omitting this phenomenon causes higher overs-

hoot during ﬂight attitude stabilisation.

Every mentioned approach has its own advanta-

ges and disadvantages since there is no perfect rou-

tine. A hybrid and ﬂexible method described in the

next section constitutes the novel and safe approach

to selecting initial parameters of the ﬂight controllers

with the high success rate preserved.

Proposed tuning process was used in various mo-

diﬁcations of the control algorithm in the Falcon V5

platform and during initial tuning of the Kruk UAV.

Both vehicles, shown in the Fig. 1, are quite different

in the terms of size, payload capabilities and conﬁgu-

ration of the propulsion system. The Falcon V5 UAV

was developed as an indoor research aerial platform

with extended lift capabilities. It is equipped with 8

motor-propeller sets arranged on 4 symmetrical arms

in the coaxial conﬁguration. Such approach allowed

to achieve up to 6kg of maximum thrust force within

2.7kg of the UAV’s own mass. Payload capabilities

reach up to 1kg of equipment with the ﬂight time of 12

minutes. On the other hand, the Kruk UAV is desig-

ned as asymmetrical hexacopter with heterogeneous

propulsion system consisting of four single units and

two double, coaxial ones. This UAV has the ability to

lift several kilograms of payload with the ﬂight time

extended up to 40 minutes. However, both vehicles

were successfully developed, tuned and tested thanks

to the procedure described in this article.

3 METHOD DESCRIPTION

The proposed method is based on a fusion of previ-

ously mentioned solutions. It uses simple models of

propulsion units, gathered from the test bench, and

physical information about hardware from the CAD

software. This approach, connected with experimen-

tal veriﬁcation on the rotary test stand, results with in-

creased safety of tuning process, especially with high

thrust platforms.

As mentioned above, the ﬁrst element of the pro-

cedure is a model of the propulsion unit. It is develo-

ped on the basis of measurements from the propulsion

analysis system presented in (Aszkowski et al., 2017)

showed in Fig. 2. This test rig provides measure-

ments of thrust, reaction torque, angular velocity and

power consumption in relation to the duty cycle of

the control signal. Such equipment is especially use-

ful in case of coaxial propulsion units, which are way

harder to model in a mathematical manner. Sensors

of the propellers’ angular velocity are rarely available

on the multirotor UAVs, therefore all models have to

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

466

Figure 1: Comparison of Falcon V5 (upper) and Kruk (lo-

wer) UAVs.

be based on the duty cycle of PWM signal as a control

input.

Next step is a simulation development phase. Fir-

stly, it is performed separately for each sub-controller

(Roll, Pitch, Yaw rotation and vertical movement).

Then, the simulation is extended into the full attitude

and vertical movement control. At this point, depen-

dencies between controllers are taken into conside-

ration. In the developed simulation, some additional

blocks are required. First one is a preset signal gene-

ration block which delivers operator command inputs

to the second block - control algorithms. Finally, data

acquisition and presentation block is required to com-

pare tuning results. In rotation and movement model

section, there are parameters deﬁning noise amplitude

on the output signals, which highly affect the perfor-

mance of control algorithms. Those parameters have

to be estimated, but it is better to marginally overesti-

mate than underestimate. In this step, tuning of men-

tioned controllers is performed with manual or auto-

matic techniques.

Figure 2: Propulsion analysis system used in modelling pro-

cess.

Next step is an experimental veriﬁcation on the

test stand. This phase allows to correct noise para-

meters and ﬁt simulation to the real environment if

needed. If propulsion unit models were formulated

correctly and physical parameters of the structure re-

mained unchanged, selected parameters should allow

the platform to maintain stability. This stage is usu-

ally performed for Roll and Pitch axes because it is

the most popular conﬁguration of rotary test benches.

Moreover, it is hard to construct the test stand with

rotation about Yaw axis and changing altitude, which

would have a negligible effect on the platform mo-

vement.

After those steps, full movement simulation can

be utilised and all parameters of controllers can be

modiﬁed to meet desired performance. In this step,

vibration parameters should be slightly increased to

eliminate the dampening effect of the test stand. It

is important to tune controllers in a cautious manner,

because too aggressive parameters in the real environ-

ment may cause instability. It is important to mention,

Initial Tuning Procedure for Attitude and Vertical Movement Controllers in Multirotor Aerial Vehicles with Heterogeneous Propulsion Units

467

that on every step of simulations or experimental veri-

ﬁcation it is possible to implement corrections in pa-

rameters to adapt to the real behaviour and meet stated

requirements. Summary of the proposed method was

shortened into following points:

1. Physical CAD modelling of multirotor UAV;

2. Propulsion units experiments on the test rig;

3. Development of models of propulsion units;

4. Formulation of separate simulations for each mo-

vement axes;

5. Implementation of controllers and tuning process;

6. Experimental veriﬁcation of simulation on the test

stand;

7. Correction of tuned parameters (optional);

8. Formulation of full attitude with vertical mo-

vement simulation;

9. Correction of tuned parameters (optional);

10. Experimental veriﬁcation during free ﬂight tests;

11. Correction of tuned parameters (optional).

4 MODELLING OF PROPULSION

UNITS

In a majority of mathematical models, the thrust force

generated by propulsion unit is represented by Eq. 1.

= b

· ω

; (1)

where: F

- force generated by i − th propulsion unit,

- scaling factor, ω

- angular velocity of a propeller.

This method is applicable only to single propulsion

units, which makes harder to represent coaxial setup

with tractor-pusher propeller pair. In addition, in most

cases, no information about the rotational speed is

available in the most UAV sensory systems. There-

fore it has to be omitted and extracted from the PWM

control signal, as the ESCs (Electronic Speed Regu-

lators) keep the blade velocity constant in relation to

the control signal.

Tests were performed on the thrust analysis sy-

stem (Aszkowski et al., 2017) for propulsion units de-

dicated to both considered platforms. Based on gat-

hered data, models were formulated. Thrust model of

units implemented in Falcon V5 platform was deve-

loped in (Ga¸sior et al., 2016b). The same procedure

was applied to the ones mounted in Kruk UAV. Block

diagram of mentioned modelling method is shown in

Fig. 3. Two duty cycle signals and supply voltage

measurements are processed by Takagi-Sugeno fuzzy

system, which calculates the thrust. The same met-

Figure 3: Block diagram of a coaxial propulsion unit model.

hod was used in modelling of the reaction torque of

coaxial propulsion unit, which is essential to develop

the simulation of Yaw movement. However, thrust

and reaction force for single propulsion units were

approximated by two dimensional polynomial (x − y,

duty cycle - voltage, with orders for each axis of 3 and

1 respectively).

5 SIMULATIONS

As stated earlier, there are four main areas of develo-

ped simulations during described tuning workﬂow:

• Roll and Pitch;

• Yaw;

• Vertical movement;

• Roll, Pitch, Yaw and vertical movement in one.

Separated simulations for each axis are formulated

with the Euler’s dynamics equation of a rigid body:

τ = Iα +(ω × Iω), (2)

where: τ - applied torques, α - angular accelerations

of the body, ω - angular velocities of the body and I

- the matrix of moments of inertia. Formulation for

angular accelerations is gathered after several opera-

tions:

α = I

−1



τ − (ω × Iω)



. (3)

Reducing above equations to single axis (ω

= ω

= 0

and α

= α

= 0 in case of an X axis) is following:

. (4)

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

468

Torques are calculated from forces generated by each

propulsion unit and distance from selected symmetry

axis:

τ =

i<n

∑

i=0

· F

, (5)

where: n - number of propulsion units, d

- distance

of propulsion unit from rotation axis and F

- force

generated by i-th propulsion unit. Positions of each

propulsion unit is gathered from CAD model along

with moments of inertia. Symmetric axes, if possible,

are located the same way as an on-board AHRS (Atti-

tude and Heading Reference System). Torque around

Yaw axis is calculated from the Eq. 5 with reaction

forces generated by each propulsion system and pla-

nar distances to them.

The general method of the single axis simulation

development was presented in (Gasior et al., 2017),

where tuning process of cascade controllers for Fal-

con V5 platform was performed. In the same paper,

the adequacy of simulation has been proven for the

stated platform. As it has been mentioned in Sec. 3,

the ﬁrst phase of initial tuning is a development of se-

parate simulations for Roll, Pitch, Yaw and vertical

movement. This usually comes down to calculating

angular or vertical acceleration based on generated

thrust and double integrating to gather velocity and

position. Fusion of this method along with additio-

nally required blocks merges into the full simulation.

Simulation results of the rotary test bench for the Kruk

platform with a comparison to the experimental data

are shown in Fig. 4. Presented case is performed on

tuned parameters, which also have been used in real

experiment. This example validates the possibility to

tune controllers on the basis of simulation. As can be

seen, tracking quality is satisfactory and squared error

characteristics are very close between two presented

cases.

After tuning and validating controllers in all men-

tioned axes separately, there is a need to merge all

of them into the one system. The overall block dia-

gram of all four simulation components is presented

in Fig. 5. Preset signals are artiﬁcially generated or

recreated from recorded ﬂight sequences and passed

to the control block. This section is responsible for

calculating appropriate control signals for propulsion

units. The control structure is design-dependant and

should be identical to the one implemented in avionics

software. The output of this block consists of eight

duty cycle signals which are also design-dependant.

In Falcon V5 and Kruk platform there are always eight

motors implemented, divided into four or six propul-

sion unit respectively. Next step is a calculation of

generated thrust and reaction force, which are there-

after transformed into angular and vertical accelerati-

75 80 85 90

Pitch [°]

-20

-10

Preset

Real

Simulation

Time [s]

75 80 85 90

Figure 4: Results of the control performance of platform

Kruk in Pitch axis during simulation and real experiment on

the test bench.

ons based on physical parameters from CAD model.

Finally, double integration in both cases allows gat-

hering velocities and positions. In each output, the

noise is added to adapt them to real conditions. These

signals close the loop for the implemented control-

lers. Every simulation is executed with the frequency

equal to the refresh rate of a control loop in the main

on-board controller.

Tuning process should be performed sequentially,

one controller at a time. Parameters selected in the

individual simulations should be used as initial ones

in the merged simulation. Experimental veriﬁcation

is described in the following section.

6 EXPERIMENTS AND TUNING

RESULTS

With the fully developed and tuned simulations, the

next step is to conduct experimental validation. The

ﬁrst phase was performed on the rotary test stand sho-

wed in Fig. 6. This device ﬁxes the UAV movement

and reduces degrees of freedom to only one rotatio-

nal axis. In this conﬁguration, Roll and Pitch con-

trollers can be validated. Exemplary characteristics

from one experiment with Kruk platform are presen-

ted in Fig. 4, where Pitch axis was concerned. As can

be seen, the controller has a good performance and

maintains tracking during the whole sequence. The

squared error remains within reasonable limits. The

Initial Tuning Procedure for Attitude and Vertical Movement Controllers in Multirotor Aerial Vehicles with Heterogeneous Propulsion Units

469

Figure 5: Block diagram of Roll, Pitch, Yaw and vertical movement simulation.

Figure 6: Platform Kruk mounted on the test stand in Pitch

axis.

highest points in error characteristics are present du-

ring rapid changes in preset signal, where controllers’

response is slightly slower.

After positive veriﬁcation on the test bench, the

oncoming step is a free ﬂight experiment performed

in order to check the performance of the Yaw and ver-

tical movement controllers. It is advised to implement

them sequentially, ﬁrstly Roll, Pitch and Yaw with

throttle control, and ﬁnally with vertical movement

turned on. This approach reduces the number of pos-

sible errors during implementation and allows to lo-

cate them more accurately. Three characteristics from

exemplary free ﬂight are presented in Fig. 7, 8 and 9,

representing Roll, Pitch and Yaw respectively. Con-

trollers with parameters selected during the simula-

tion phase managed to correctly track preset signal

which was very dynamic because of a characteristic

of the performed mission. Errors in all three exam-

ples were comparable, but the highest divergence has

been observed in Yaw controller. This could be the

result of wind gusts during ﬂying through corridors.

450 500 550 600

Roll [°]

-4

-2

Angle Preset

Time [s]

450 500 550 600

Figure 7: Results of the control performance of platform

Kruk in Roll axis during real ﬂight.

Experiments on controllers of vertical velocity has

been performed in (Gasior et al., 2017) for Falcon V5

platform. Unfortunately, these experiments have not

been completed so far for the Kruk UAV.

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

470

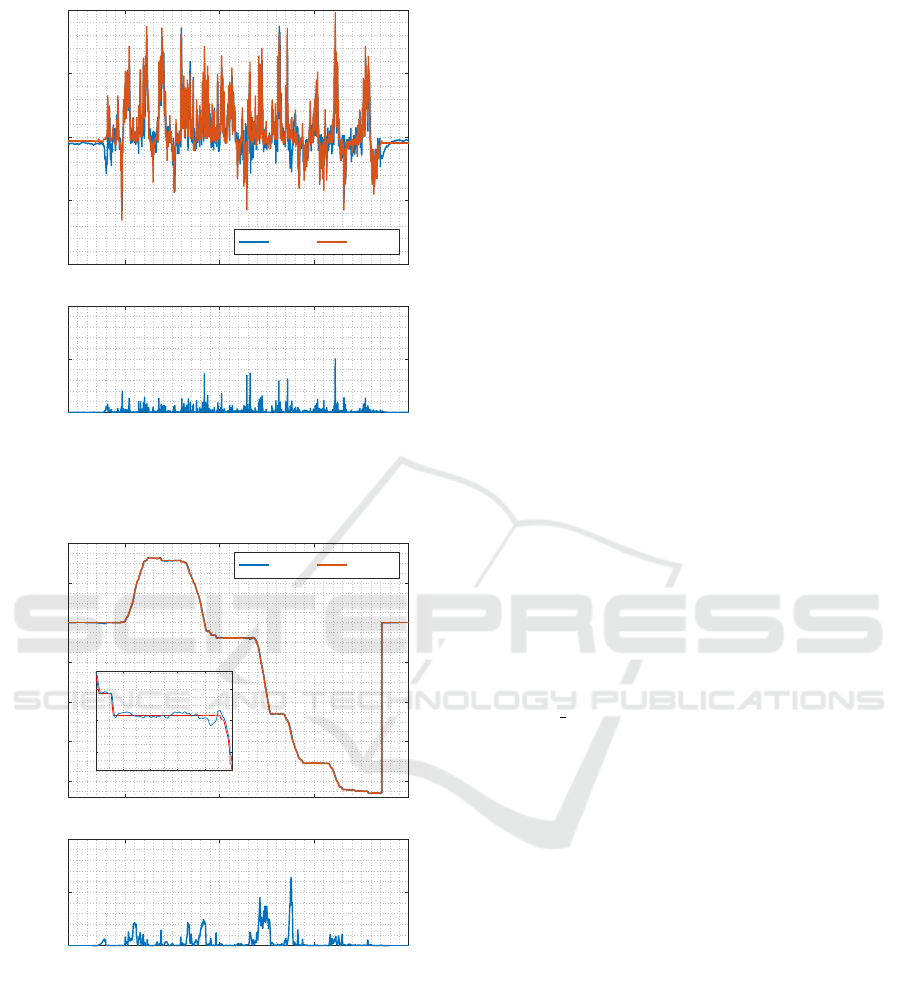
450 500 550 600

Pitch [°]

-4

-2

Angle Preset

Time [s]

450 500 550 600

Figure 8: Results of the control performance of platform

Kruk in Pitch axis during real ﬂight.

450 500 550 600

Yaw [°]

-200

-150

-100

-50

100

Angle Preset

500 505 510 515

-25

-20

-15

Time [s]

450 500 550 600

Figure 9: Results of the control performance of platform

Kruk in Yaw axis during real ﬂight.

7 CONCLUSIONS AND FUTURE

WORK

Presented method of initial tuning of the controllers’

parameters proven itself in real life scenarios. It was

tested during modiﬁcation of control scheme for the

Falcon V5 platform and initial tuning for the Kruk

UAV. It is important to mention, that the complete

model of analysed multirotor UAV is not required to

achieve satisfactory results. This affects the develop-

ment time, which can be reduced by eliminating the

calibration process of the mentioned model.

One of the key points of the described method is

a model of propulsion unit, which is the foundation

to all of the simulations. Thanks to its ﬂexibility, this

method is extremely useful to simulate unsymmetri-

cal platforms with heterogeneous propulsion units.

In the future work, authors plan to ﬁnish the ex-

perimental veriﬁcation process of the vertical mo-

vement controller for the Kruk UAV. Moreover, com-

parison with state-of-the-art initial tuning techniques

will be performed. Finally, automatic tuning algo-

rithms for different types of controllers will be im-

plemented to simplify comparison process and para-

meterise tracking performance with an adequate cost

function.

ACKNOWLEDGEMENTS

This research was funded by the Poznan Univer-

sity of Technology grant DSPB/0162. In addition,

part of this work concerning the Kruk platform,

was co-ﬁnanced by the European Regional Develop-

ment Fund under the Smart Growth Operational Pro-

gramme 2014-2020 under the Operation 1.2 - Contest

1/1.2/2015 INNOLOT.

REFERENCES

Aszkowski, P., Błoszyk, K., Bondyra, A., Ga¸sior, P., and

Giernacki, W. (2017). UAV propulsion analysis sy-

stem with reconﬁgurable controller feature. Measure-

ment Automation Monitoring, 63(5):171–173.

Bondyra, A., Gardecki, S., Ga¸sior, P., and Giernacki, W.

(2016). Performance of coaxial propulsion in design

of multi-rotor UAVs. In Challenges in Automation,

Robotics and Measurement Techniques, pages 523–

531. Springer.

Bondyra, A., Gasior, P., and Gardecki, S. (2017). Experi-

mental test bench for multirotor UAVs. In Internatio-

nal Conference Automation, pages 330–338. Springer.

Bouabdallah, S. and Siegwart, R. (2007). Full control of

a quadrotor. In Intelligent robots and systems, 2007.

IROS 2007. IEEE/RSJ international conference on,

pages 153–158. Ieee.

Connor, J., Seyedmahmoudian, M., and Horan, B. (2017).

Using particle swarm optimization for PID optimiza-

tion for altitude control on a quadrotor. In Univer-

sities Power Engineering Conference (AUPEC), 2017

Australasian, pages 1–6. IEEE.

Initial Tuning Procedure for Attitude and Vertical Movement Controllers in Multirotor Aerial Vehicles with Heterogeneous Propulsion Units

471

Dikmen,

I. C., Arisoy, A., and Temeltas, H. (2009). Attitude

control of a quadrotor. In Recent Advances in Space

Technologies, 2009. RAST’09. 4th International Con-

ference on, pages 722–727. IEEE.

Ga¸sior, P., Bondyra, A., Gardecki, S., and Giernacki, W.

(2016a). Robust estimation algorithm of altitude and

vertical velocity for multirotor UAVs. In Methods

and Models in Automation and Robotics (MMAR),

2016 21st International Conference on, pages 714–

719. IEEE.

Ga¸sior, P., Bondyra, A., Gardecki, S., Giernacki, W., and

Kasi

nski, A. (2016b). Thrust estimation by fuzzy mo-

deling of coaxial propulsion unit for multirotor UAVs.

In Multisensor Fusion and Integration for Intelligent

Systems (MFI), 2016 IEEE International Conference

on, pages 13–18. IEEE.

Gasior, P., Bondyra, A., Gardecki, S., and Kasinski, A.

(2017). Cascade control algorithms of position and

attitude for multirotor UAV. In Methods and Models

in Automation and Robotics (MMAR), 2017 22nd In-

ternational Conference on, pages 47–52. IEEE.

Hoffmann, F., Goddemeier, N., and Bertram, T. (2010).

Attitude estimation and control of a quadrocop-

ter. In Intelligent Robots and Systems (IROS), 2010

IEEE/RSJ International Conference on, pages 1072–

1077. IEEE.

Howard, D. (2017). A platform that directly evolves multi-

rotor controllers. IEEE Transactions on Evolutionary

Computation, 21(6):943–955.

Panizza, P., Invernizzi, D., Riccardi, F., Formentin, S., and

Lovera, M. (2016). Data-driven attitude control law

design for a variable-pitch quadrotor. In American

Control Conference (ACC), 2016, pages 4434–4439.

IEEE.

Tayebi, A. and McGilvray, S. (2006). Attitude stabilization

of a VTOL quadrotor aircraft. IEEE Transactions on

control systems technology, 14(3):562–571.

Wang, L. and Poksawat, P. (2017). Automatic tuning of

hexacopter attitude control systems with experimen-

tal validation. In System Theory, Control and Com-

puting (ICSTCC), 2017 21st International Conference

on, pages 753–758. IEEE.

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

472