Clustering-based Under-sampling for Software Defect Prediction

Moheb M. R. Henein, Doaa M. Shawky and Salwa K. Abd-El-Haﬁz

Engineering Mathematics and Physics Department, Faculty of Engineering, Cairo University, Giza, 12613, Egypt

Keywords:

Software Defect Prediction, Under-sampling, Clustering, K-means, Artiﬁcial Neural Network.

Abstract:

Detection of software defective modules is important for reducing the time and resources consumed by soft-

ware testing. Software defect data sets usually suffer from imbalance, where the number of defective modules

is fewer than the number of defect-free modules. Imbalanced data sets make the machine learning algorithms

to be biased toward the majority class. Clustering-based under-sampling shows its ability to ﬁnd good repre-

sentatives of the majority data in different applications. This paper presents an approach for software defect

prediction based on clustering-based under-sampling and Artiﬁcial Neural Network (ANN). Firstly, clustering-

based under-sampling is used for selecting a subset of the majority samples, which is then combined with the

minority samples to produce a balanced data set. Secondly, an ANN model is built and trained using the

resulted balanced data set. The used ANN is trained to classify the software modules into defective or defect-

free. In addition, a sensitivity analysis is conducted to choose the number of majority samples that yields the

best performance measures. Results show the high prediction capability for the detection of defective modules

while maintaining the ability of detecting defect-free modules.

1 INTRODUCTION

The main purpose of software defect prediction (SDP)

is to classify a software module into defective or

defect-free based on some calculated software met-

rics, and without being intensively tested. Hence, it

reduces both the time and resources that are needed

for the testing process before the software release. An

ideal SDP should correctly classify all modules. Typ-

ically, two classiﬁcation errors may occur; the ﬁrst

one originates from classifying a defective module as

defect-free, meanwhile the second error results from

classifying a defect-free module as defective. The

ﬁrst type is more risky as it causes failures to the

software after release. Also, the second type slows

down the process of releasing software, because the

modules classiﬁed as defective are subject to test-

ing and maintenance, hence, additional time and re-

sources are consumed. One of the most challenging

problems facing SDP is the data imbalance. Almost

all SDP data sets suffer from high imbalance ratio be-

tween the defect-free and defective modules. Most of

the software modules are defect-free, thus, they rep-

resent the majority class. Meanwhile, the defective

modules represent the minority class. Data imbal-

ance is the main cause of the ﬁrst type of classiﬁca-

tion errors, due to the weak representation of the mi-

nority class with respect to the majority class. Since

data imbalance leads the classiﬁer to be biased to-

ward the majority class, it is a serious problem that

needs to be considered carefully in the context of

SDP. Previously, different imbalance learning tech-

niques were applied to SDP (Menzies et al., 2008;

Zheng, 2010; Khoshgoftaar et al., 2010; Riquelme

et al., 2008; Kamei et al., 2007). Class imbalance

learning techniques are divided into two main cate-

gories, namely data level and algorithm level (He and

Garcia, 2009). Data level techniques, also known as

preprocessing techniques, are dealing with the skew-

ness of data by over-sampling the minority class or

under-sampling the majority class or hybrid under-

sampling and over-sampling. Algorithm level tech-

niques, on the other hand, emphasize the minority

samples through assigning higher weights compared

to the majority samples in the learning or the clas-

siﬁcation processes. In (Wang and Yao, 2013), ﬁve

class imbalance learning methods were applied with

two software defect prediction classiﬁers on NASA

MDP data sets (Chapman et al., 2004). The two soft-

ware defect predictors are Na

ıve Bayes with log ﬁl-

ter (NB), and Random Forest (RF). The ﬁve class

imbalance learning methods include random under-

sampling (RUS), balanced random under-sampling

(RUS-bal), threshold-moving (THM), SMOTEBoost

Henein, M., Shawky, D. and Abd-El-Haﬁz, S.

Clustering-based Under-sampling for Software Defect Prediction.

DOI: 10.5220/0006911401850193

In Proceedings of the 13th International Conference on Software Technologies (ICSOFT 2018), pages 185-193

ISBN: 978-989-758-320-9

185

(SMB), and AdaBoost.NC (BNC). RUS and RUS-bal

belong to data-level methods. THM is a cost sen-

sitive classiﬁer belonging to algorithm level. SMB

and BNC are ensemble classiﬁers. In (Arar and Ayan,

2015), the authors used a cost sensitive ANN, where

traditional error functions (mean square error, least

square error, relative absolute error, etc.) were re-

placed by Normalized Expected Costed of Misclas-

siﬁcation (NECM), which is given by (1).

NECM = FPR × P

nd p

× FNR × P

d p

(1)

Where FPR and FNR are the calculated false pos-

itive and false negative rates, respectively, P

nd p

and

d p

are the prior percentage of non-defect prone and

defect prone, respectively, and the term

deﬁnes

the ratio between the costs of false negative error

to false positive error. Due to the imbalance prop-

erty, this term controls the trade-off between two

types of accuracy, overall accuracy and positive de-

tection accuracy. The training process of the ANN

adjusts the weights between neurons using Artiﬁcial

Bee Colony (ABC) based on the back-propagated

error from NECM equation.In this paper, we apply

the clustering-based approach that was introduced in

(Lin et al., 2017), for under-sampling the majority

samples. The clustering-based under-sampling ap-

proach is based on balancing an imbalanced data set

by reducing the majority class size to the size of

the minority class. Majority data samples are clus-

tered into number of clusters equivalent to the num-

ber of minority data. Then, for each cluster, only

one sample is selected to replace the whole cluster.

Clustering-based under-sampling can efﬁciently rep-

resent the whole majority data by a selected subset

instead of random under-sampling. Clustering-based

under-sampling combined with different classiﬁers

showed high prediction ability on different data sets

in different applications, such as breast cancer (Lin

et al., 2017) and bankruptcy prediction (Kim et al.,

2016). In this paper, we apply this promising ap-

proach with a modiﬁed strategy for the selection of

majority data subset for balancing the data sets in the

context of SDP. In this strategy, the clusters’ represen-

tatives are selected in an iterative approach in order to

ensure that the sample was selected at most once. The

rest of the paper is organized as follows: Section 2

discusses the proposed approach. Section 3 describes

the evaluation of the proposed approach in detail, in-

cluding the description of the used data sets, perfor-

mance measures, and the conducted experiments. Fi-

nally, conclusion and future work are given in Section

2 PROPOSED APPROACH

The proposed approach for SDP consists of the fol-

lowing steps. In the ﬁrst step, the analyzed data

sets are balanced using the clustering-based under-

sampling technique. In the second step, an ANN-

based classiﬁer is built. The built ANN model

was constructed with ten nodes in the single hidden

layer. In addition, Log-sigmoidal function is used as

the transfer function for the hidden layer, and soft-

max function as tranfer function for the output layer.

Adam is used for training the ANN (Kingma and

Ba, 2014). Adam is a gradient-based optimization of

stochastic objective functions.

The clustering-based under-sampling was introduced

in (Lin et al., 2017). The procedure is shown in Fig.

1. The imbalanced data set is divided into major-

ity and minority samples. The majority samples are

clustered, where the number of clusters is equal to

the number of minority samples. For each cluster,

the nearest neighbor sample to the cluster center is

chosen to represent the whole cluster. The clusters’

centers are not suitable for representing the cluster,

because they are artiﬁcially calculated samples (Lin

et al., 2017). However, the selection of the nearest

neighbor to clusters center might result in selecting

a sample several times due to overlapping between

clusters. Thus, for preventing duplicates, an iterative

approach for the selection of the majority representa-

tives was used by choosing a unique nearest neighbor

sample to each clusters center in each iteration. Fi-

nally, the selected nearest neighbors samples are com-

bined with the minority samples to form a balanced

data set. In this step, K-means is used for clustering.

K-means clustering algorithm is introduced in (Harti-

gan and Wong, 1979). It calculates the distances be-

tween the target data. The samples with minimum

distances between each other are grouped to form a

cluster. Thus, a cluster combines the samples with

similar characteristics.

3 EVALUATION

3.1 Data Sets

NASAs Metrics Data Program Data Repository

(MDP) is considered as a bench-mark for SDP (Chap-

man et al., 2004). Recently, it was used for the evalu-

ation of SDP models such as in (Wang and Yao, 2013;

Arar and Ayan, 2015; Kumudha and Venkatesan,

2016; L

opez et al., 2012; Liu et al., 2014; Li et al.,

2016; Jin and Jin, 2015). It contains defect data of dif-

ferent projects implemented using C, C++, and Java.

ICSOFT 2018 - 13th International Conference on Software Technologies

186

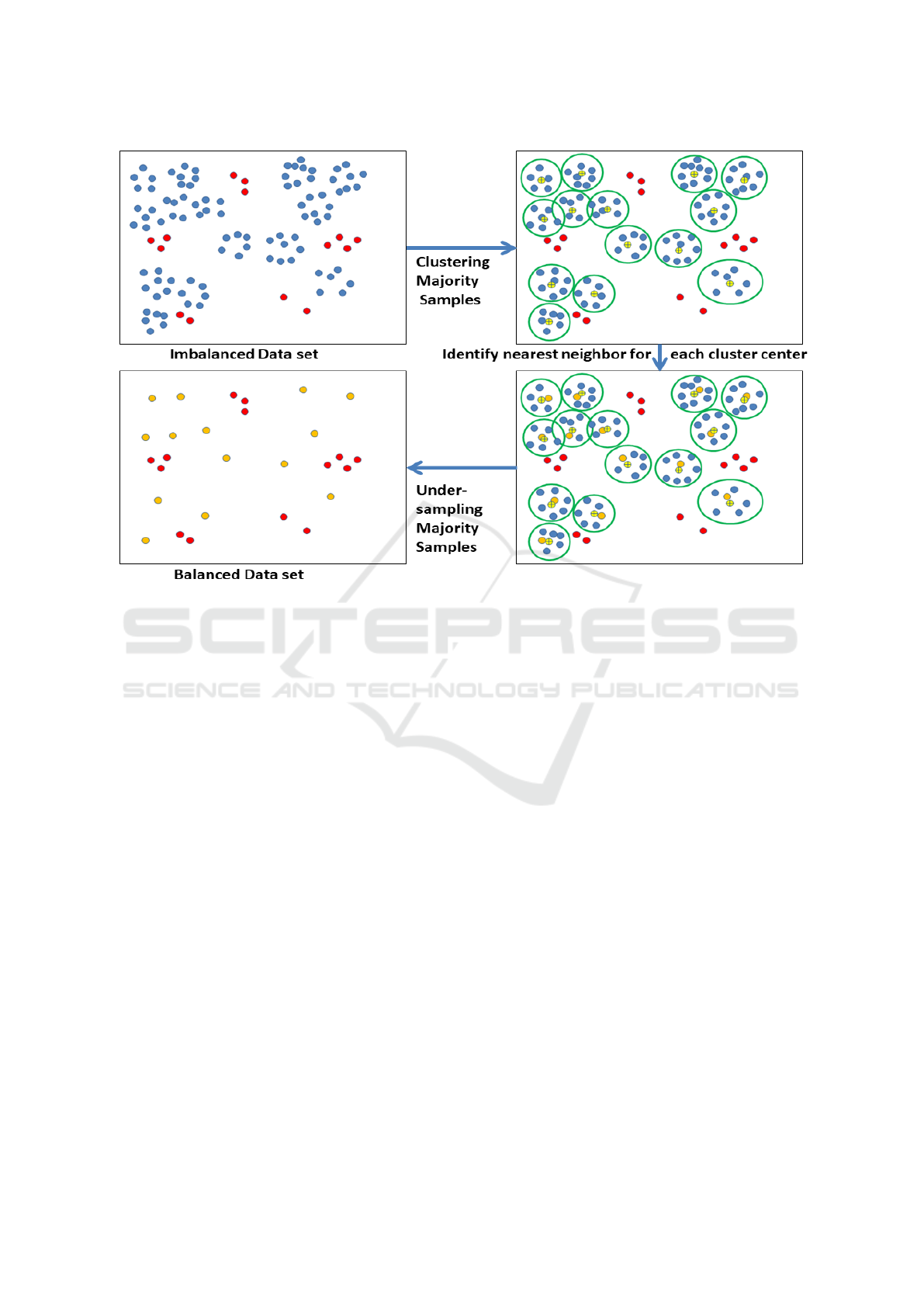
Figure 1: Clustering-based Under-sampling majority samples.

The projects have different sizes and defect ratios.

The software modules are described using different

attributes such as McCabe measures (McCabe, 1976)

and Halstead measures (Halstead, 1977). In this pa-

per, ﬁve NASA MPD data sets were selected for the

evaluation of the proposed approach. Since these data

sets were selected by recent similar approaches, we

have applied our proposed approach on them to be

able to conduct a fair comparison. Some descriptions

about the selected data sets from PROMISE reposi-

tory (available at http://promisedata.org/) are shown

in Table 1.

3.1.1 Data Preprocessing

Three preprocessing steps were ﬁrstly performed on

the data sets. These steps are recommended by (Gray

et al., 2012; Shepperd et al., 2013) and include the

following:

1. Removing duplicated samples with the same fea-

ture values.

2. Replacing unavailable values by the mean value

of the corresponding feature.

3. Normalizing the feature values. In this paper, a

quantile transformer is used for each feature inde-

pendently by mapping the data to a uniform distri-

bution with values between 0 and 1. This is a non

linear transformation which reduces the impact of

marginal outliers (Pedregosa et al., 2011)

3.2 Performance Measurement

3.2.1 Confusion Matrix

Different performance measurements based on the

confusion matrix are used in the software defect pre-

diction domain for reporting and comparing the re-

sults of different techniques (He and Garcia, 2009;

Wang and Yao, 2013; Arar and Ayan, 2015; Ku-

mudha and Venkatesan, 2016; L

opez et al., 2012;

Liu et al., 2014; Li et al., 2016; Jin and Jin, 2015;

Abaei et al., 2015). Table 2 shows a typical confu-

sion matrix where the defect-prone and the defect-free

are considered as positive and negative, respectively.

Confusion matrix for binary classiﬁcation is formed

by four cells namely, the number of positive modules

truly classiﬁed (T P), the number of positive modules

falsely classiﬁed (FP), the number of negative mod-

ules falsely classiﬁed (FN), and the number of neg-

ative modules truly classiﬁed (T N). The following

measurements are calculated based on the elements

of the confusion matrix.

• Overall Accuracy

Accuracy measures the ratio of the truly classiﬁed

samples to the total number of samples as given by

Clustering-based Under-sampling for Software Defect Prediction

187

Table 1: NASA MDP data sets description.

Data Description Language Number of Percentage of

set Modules defective modules

CM1 Spacecraft instrument C 498 9.83

KC2 Storage management C++ 522 20.49

for ground data

PC1 Flight software C++ 1109 6.94

for earth

orbiting satellite

KC1 Storage management C++ 2109 15

for ground data

JM1 Real-time predictive C 10885 21.4

ground system

Table 2: Confusion Matrix.

Predicted

Actual

Defect-Prone Defect-Free

Defect-Prone True Positive False Positive

T P FP

Defect-Free False Negative True Negative

FN T N

(2). Accuracy can have values between zero and

one, where accuracy values closer to one mean

that the classiﬁer has a better prediction perfor-

mance.

Accuracy =

T P + T N

T P + FP + T N + FN

(2)

• Probability of Detection (PD) or True Positive

rate(T PR)

PD is the ratio of the actual positive samples truly

classiﬁed to the total number of actual positive

samples as given by (3). PD values closer to one

mean that the classiﬁer has a better prediction per-

formance.

PD = T PR =

T P

T P + FN

(3)

• Probability of False Alarm (PF) or false positive

rate (FPR)

PF is the ratio of the actual negative samples

falsely classiﬁed to the total number of actual neg-

ative samples as given by (4). PF closer to zero

means that classiﬁer has better prediction perfor-

mance.

PF = FPR =

FP + T N

(4)

• Balance

Balance combines PF and PD into one measure.

It is deﬁned as the Euclidian distance from the real

point (PD, PF) to the ideal point (PF = 0, PD =

1) as given by (5). Balance is expected to be high

for a good predictor.

Balance = 1 −

(0 − PF)

+ (1 − PD)

(5)

• F1-measure

F1-measure is calculated based on confusion ma-

trix’ elements as given by (6). F1-measure closer

to one means that classiﬁer has better prediction

performance.

F1 =

2 ∗ (

T P

T P+FP

∗

T P

T P+FN

)

(

T P

T P+FP

T P

T P+FN

)

(6)

3.2.2 Receiver Operating Characteristics Curve

(ROC)

ROC curve illustrates the trade-off between the proba-

bility of detection (PD) and the false alarm rates (PF).

It is used in the performance evaluation of a classiﬁer

across all possible decision thresholds. Values of area

under curve (AUC) lie between 0 and 1 (Huang and

Ling, 2005; Bradley, 1997). It is equivalent to the

probability that a randomly chosen sample of the pos-

itive class will have lower estimated probability to be

misclassiﬁed than a randomly chosen sample of the

negative class. A good predictor should have a high

AUC value.

3.3 Experiments and Results

Two experiments were performed on the selected data

sets. The ﬁrst experiment evaluates the performance

ICSOFT 2018 - 13th International Conference on Software Technologies

188

of the proposed balancing approach combined with

ANN. The effect of the number of under-sampling

majority samples was investigated in the second ex-

periment. The experiments were performed using 5-

fold cross validation repeated 10 times for reporting

the mean results, which resulted in 50 runs, in order

to test the robustness of the proposed model by select-

ing different random learning and testing sets for each

run. The experiments were performed using Python,

where scikit-learn library was used for K-means and

performance measures calculation (Pedregosa et al.,

2011). ANN was built using tensorﬂow with three

layers; namely input layer, hidden layer, and output

layer. Moreover, log-sigmoidal function was used as

transfer function of the hidden layer, that consists of

10 neurons, meanwhile the softmax function is used

as transfer function for the output layer.

3.3.1 Experiment 1

In the ﬁrst experiment, the data set was balanced by

selecting the number of majority clusters to be equal

to the number of minority samples. Then, each clus-

ter of the majority samples was replaced by a single

sample. The nearest sample to each cluster center was

selected to replace the whole cluster elements. Se-

lection of the clusters’ representatives was performed

in sequence to ensure that the sample was selected

at most once. The selected sample is the nearest

neighbor to the cluster’ center, which should be se-

lected only once. Figures 2- 6 show the box plots

of the calculated performance measures for each data

set for the 50 runs. The calculated mean and the

95% conﬁdence interval of performance measures are

given in Table 3. Results show that the proposed

approach is suitable for small scale data sets (CM1,

PC1, and KC2), where the achieved PD values are

greater than 0.7, and PF values are smaller than or

equal to 0.3, also AUC values are around 0.8. Fig-

ures 2-4 show that the proposed approach succeeded

in correctly predicting the defective modules (PD = 1

for some runs). Also, the best achieved PF value for

the small scale data sets is equal to 0.2. Thus, the

results show the ability of the proposed approach to

detect the defective modules while maintaining good

capability for the detection of the defect-free mod-

ules. However, the calculated performance measures

for the relatively large-scale data sets (KC1 and JM1),

are worse than those of the small scale data sets’. Al-

though, the obtained measures for detecting the de-

fective modules are acceptable, since PD values are

greater than or equal to 0.65. The main drawback of

the proposed approach appears in the PF values of the

large data sets, where the PF values are greater than

0.4. The relatively high PF values means that the pro-

Figure 2: CM1 performance measurement box plots.

Figure 3: KC2 performance measurement box plots.

posed approach misclassiﬁed some of the defect-free

modules. This can be explained by the loss of infor-

mation about the defect-free modules in the sampling

process, which increases as the size of the data set in-

creases since more samples are removed in this case.

To address this, experiment 2 was conducted.

3.3.2 Experiment 2

In this experiment, a sensitivity study was conducted

by using different numbers of clusters to show the ef-

fect of changing the number of majority class sam-

ples on the overall performance of the proposed sys-

tem. Figures 7-11 show the inﬂuence of varying the

number of selected defect-free samples (clusters) on

the performance of the proposed approach using K-

means. As the number of defect free samples in-

creases, while having

the same number of defective samples, the detec-

tion of the defect free modules increases and the de-

tection of the defective modules decreases. Hence,

PD is inversely proportional to the difference be-

tween defect-free and defective samples denoted by

K. However, K is directly proportional to accuracy,

Clustering-based Under-sampling for Software Defect Prediction

189

Table 3: Mean values using 95% conﬁdence interval of performance measures achieved by the proposed approach using

K-means for clustering.

Data set PD PF Balance Accuracy AUC F1

CM1 0.836 ± 0.042 0.310 ± 0.014 0.780 ± 0.01 0.706 ± 0.015 0.781 ± 0.028 0.390 ± 0.023

PC1 0.771 ± 0.049 0.249 ± 0.014 0.731 ± 0.0069 0.753 ± 0.014 0.832 ± 0.022 0.318 ± 0.021

KC2 0.754 ± 0.037 0.254 ± 0.021 0.820 ± 0.014 0.748 ± 0.013 0.856 ± 0.0058 0.617 ± 0.019

KC1 0.690 ± 0.028 0.479 ± 0.018 0.540 ± 0.0089 0.566 ± 0.014 0.677 ± 0.02 0.458 ± 0.016

JM1 0.654 ± 0.012 0.406 ± 0.011 0.630 ± 0.0061 0.607 ± 0.0075 0.668 ± 0.0053 0.431 ± 0.0055

Figure 4: PC1 performance measurement box plots.

Figure 5: KC1 performance measurement box plots.

balance, and AUC. Increasing the number of samples

for a class enhances the ability of predicting this class.

Thus, K can be used as a control parameter which

makes SDP model biased toward the detection of de-

fect or defect-free classes. Therefore, based on the

deﬁned costs of misclassiﬁcation, K can be selected

to minimize the overall cost. Also, a moderate value

of K can be selected in order to have a good accuracy,

balance, and AUC values while having an acceptable

PD value. Thus, performance measures were calcu-

lated at different values of K from −25 to 25 with

step size equals to 5, where the 0 value determines the

balanced data set having the number of selected ma-

jority samples equal to the number of minority sam-

ples. This interval is chosen to test the sensitivity of

the proposed approach to the number of selected ma-

Figure 6: JM1 performance measurement box plots.

jority samples around the balanced data set, and to

prevent the classiﬁer from being biased toward any of

the two classes. As shown in ﬁgures 7-11, for each of

the data sets, the best achieved performance measures

appear at different values of K. Table 4 shows the

best achieved performance measures when K is var-

ied from −25 to 25 on each data set. The results show

that higher performance measures can be obtained at

different values of K.

In addition, Table 5 shows the selected values of

K for each data set, where the selected value achieves

low PF while maintaining high PD. Since the AUC

and Balance are calculated in terms of PD and PF,

therefore the selected values of K can be considered

as the best achieving performance. Hence, K can be

determined in the validation process to achieve high

performance measures. In addition, Table 6 shows

the obtained performance using the selected values of

K in comparison with similar approaches. The com-

pared approaches include algorithm level and data

level techniques. The algorithm level techniques in-

clude ABC-ANN (Arar and Ayan, 2015), and DNC

(Wang and Yao, 2013), meanwhile the used data level

techniques are Random Under Sampling (RUS) and

RUS-bal (Wang and Yao, 2013) . The best result

for each measure is highlighted in bold. As shown

in the table, the proposed approach outperformed the

sampling approaches (RUS and RUS-bal). Also, the

results of the performance measures are comparable

to the cost sensitive learning approaches (ABC-ANN

and DNC). ABC-ANN achieved the best PD in four

ICSOFT 2018 - 13th International Conference on Software Technologies

190

Table 4: Mean values of the best achieved performance measures for different values of K.

Data set PD PF Balance Accuracy AUC F1

CM1 0.84 0.25 0.823 0.755 0.795 0.427

PC1 0.857 0.188 0.832 0.804 0.854 0.349

KC2 0.84 0.207 0.817 0.757 0.854 0.659

KC1 0.84 0.25 0.617 0.606 0.689 0.467

JM1 0.672 0.376 0.823 0.636 0.672 0.444

Figure 7: Performance measurement for different values for

k for CM1.

Figure 8: Performance measurement for different values for

k for KC2.

Figure 9: Performance measurement for different values for

k for PC1.

out of the ﬁve data sets, but it gave the worst PF

in the ﬁve data sets. This contradiction might be

caused by the greediness of ABC-ANN in predicting

the defective modules, even if it affects the predic-

Figure 10: Performance measurement for different values

for k for KC1.

Figure 11: Performance measurement for different values

for k for JM1.

Table 5: Selected K values for data sets.

Data set Selected K

CM1 10

PC1 5

KC2 0

KC1 20

JM1 0

tion of the defect-free modules. Therefore, the pro-

posed approach outperformed ABC-ANN in Balance

and AUC measures, that are calculated based on PD

and PF measures. Moreover, the proposed approach

achieved better results on small scale data sets (CM1,

PC1, and KC2). Although the results on large scale

data sets (KC1 and JM1) are worse, the results are

comparable to the best performing techniques.

Clustering-based Under-sampling for Software Defect Prediction

191

Table 6: Performance measures of the proposed model versus the state of the art models on NASA data sets.

NASA Data set ABC-ANN RUS DNC RUS-bal Proposed Approach

CM1 0.75 NA

0.590 NA 0.84

PC1 0.89 NA 0.570 NA 0.8

KC2 0.79 NA 0.771 NA 0.754

KC1 0.79 NA 0.710 NA 0.625

JM1 0.71 NA 0.660 NA 0.625

NASA Data set ABC-ANN RUS DNC RUS-bal Proposed Approach

CM1 0.33 NA 0.226 NA 0.265

PC1 0.37 NA 0.107 NA 0.22

KC2 0.21 NA 0.216 NA 0.22

KC1 0.33 NA 0.241 NA 0.415

JM1 0.41 NA 0.314 NA 0.415

Balance

NASA Data set ABC-ANN RUS DNC RUS-bal Proposed Approach

CM1 0.71 0.526 0.577 0.577 0.809

PC1 0.73 0.636 0.682 0.688 0.813

KC2 0.79 0.705 0.777 0.709 0.748

KC1 0.72 0.659 0.733 0.677 0.617

JM1 0.64 0.646 0.241 0.642 0.607

Accuracy

NASA Data set ABC-ANN RUS DNC RUS-bal Proposed Approach

CM1 0.68 NA NA NA 0.747

PC1 0.65 NA NA NA 0.782

KC2 0.79 NA NA NA 0.748

KC1 0.69 NA NA NA 0.6

JM1 0.61 NA NA NA 0.607

AUC

NASA Data set ABC-ANN RUS DNC RUS-bal Proposed Approach

CM1 0.77 0.622 0.787 0.622 0.774

PC1 0.82 0.726 0.866 0.739 0.829

KC2 0.85 0.730 0.828 0.726 0.856

KC1 0.80 0.710 0.818 0.713 0.672

JM1 0.71 0.665 0.766 0.658 0.668

Not Available.

4 CONCLUSION AND FUTURE

WORK

In this paper, an approach for SDP after balancing

the ratio of defective to non-defective modules is pre-

sented. The balancing is performed using clustering-

based under-sampling on the defect-free modules.

The proposed model improves the detection of the de-

fective modules without affecting the ability to detect

the defect-free modules, which is shown by the high

achieved PD results. In addition, the PF and accu-

racy were improved which means that the detection of

the defect-free modules is also improved. This proves

that clustering-based under-sampling is a good tech-

nique for the selection of a well-representative sub-

set of the majority data for SDP models. As a fu-

ture work, we will apply data samples ﬁltering for re-

moving noisy samples, especially for the large scale

data sets. Also, different clustering and learning algo-

rithms will be investigated.

REFERENCES

Abaei, G., Selamat, A., and Fujita, H. (2015). An

empirical study based on semi-supervised hybrid

ICSOFT 2018 - 13th International Conference on Software Technologies

192

self-organizing map for software fault prediction.

Knowledge-Based Systems, 74:28–39.

Arar,

O. F. and Ayan, K. (2015). Software defect predic-

tion using cost-sensitive neural network. Applied Soft

Computing, 33:263–277.

Bradley, A. P. (1997). The use of the area under the

roc curve in the evaluation of machine learning algo-

rithms. Pattern recognition, 30(7):1145–1159.

Chapman, M., Callis, P., and Jackson, W. (2004). Metrics

data program. NASA IV and V Facility, http://mdp. ivv.

nasa. gov.

Gray, D., Bowes, D., Davey, N., Sun, Y., and Christianson,

B. (2012). Reﬂections on the nasa mdp data sets. IET

software, 6(6):549–558.

Halstead, M. H. (1977). Elements of software science, vol-

ume 7. Elsevier New York.

Hartigan, J. A. and Wong, M. A. (1979). Algorithm as

136: A k-means clustering algorithm. Journal of the

Royal Statistical Society. Series C (Applied Statistics),

28(1):100–108.

He, H. and Garcia, E. A. (2009). Learning from imbalanced

data. IEEE Transactions on knowledge and data engi-

neering, 21(9):1263–1284.

Huang, J. and Ling, C. X. (2005). Using auc and accuracy

in evaluating learning algorithms. IEEE Transactions

on knowledge and Data Engineering, 17(3):299–310.

Jin, C. and Jin, S.-W. (2015). Prediction approach of soft-

ware fault-proneness based on hybrid artiﬁcial neu-

ral network and quantum particle swarm optimization.

Applied Soft Computing, 35:717–725.

Kamei, Y., Monden, A., Matsumoto, S., Kakimoto, T., and

Matsumoto, K.-i. (2007). The effects of over and

under sampling on fault-prone module detection. In

Empirical Software Engineering and Measurement,

2007. ESEM 2007. First International Symposium on,

pages 196–204. IEEE.

Khoshgoftaar, T. M., Gao, K., and Seliya, N. (2010). At-

tribute selection and imbalanced data: Problems in

software defect prediction. In Tools with Artiﬁcial

Intelligence (ICTAI), 2010 22nd IEEE International

Conference on, volume 1, pages 137–144. IEEE.

Kim, H.-J., Jo, N.-O., and Shin, K.-S. (2016). Optimiza-

tion of cluster-based evolutionary undersampling for

the artiﬁcial neural networks in corporate bankruptcy

prediction. Expert Systems with Applications, 59:226–

234.

Kingma, D. P. and Ba, J. (2014). Adam: A

method for stochastic optimization. arXiv preprint

arXiv:1412.6980.

Kumudha, P. and Venkatesan, R. (2016). Cost-sensitive ra-

dial basis function neural network classiﬁer for soft-

ware defect prediction. The Scientiﬁc World Journal,

2016.

Li, W., Huang, Z., and Li, Q. (2016). Three-way decisions

based software defect prediction. Knowledge-Based

Systems, 91:263–274.

Lin, W.-C., Tsai, C.-F., Hu, Y.-H., and Jhang, J.-S. (2017).

Clustering-based undersampling in class-imbalanced

data. Information Sciences, 409:17–26.

Liu, M., Miao, L., and Zhang, D. (2014). Two-stage cost-

sensitive learning for software defect prediction. IEEE

Transactions on Reliability, 63(2):676–686.

opez, V., Fern

andez, A., Moreno-Torres, J. G., and Her-

rera, F. (2012). Analysis of preprocessing vs. cost-

sensitive learning for imbalanced classiﬁcation. open

problems on intrinsic data characteristics. Expert Sys-

tems with Applications, 39(7):6585–6608.

McCabe, T. J. (1976). A complexity measure. IEEE Trans-

actions on software Engineering, (4):308–320.

Menzies, T., Turhan, B., Bener, A., Gay, G., Cukic, B., and

Jiang, Y. (2008). Implications of ceiling effects in de-

fect predictors. In Proceedings of the 4th international

workshop on Predictor models in software engineer-

ing, pages 47–54. ACM.

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,

Thirion, B., Grisel, O., Blondel, M., Prettenhofer,

P., Weiss, R., Dubourg, V., Vanderplas, J., Passos,

A., Cournapeau, D., Brucher, M., Perrot, M., and

Duchesnay, E. (2011). Scikit-learn: Machine learning

in Python. Journal of Machine Learning Research,

12:2825–2830.

Riquelme, J., Ruiz, R., Rodr

ıguez, D., and Moreno, J.

(2008). Finding defective modules from highly unbal-

anced datasets. Actas de los Talleres de las Jornadas

de Ingenier

ıa del Software y Bases de Datos, 2(1):67–

74.

Shepperd, M., Song, Q., Sun, Z., and Mair, C. (2013). Data

quality: Some comments on the nasa software defect

datasets. IEEE Transactions on Software Engineering,

39(9):1208–1215.

Wang, S. and Yao, X. (2013). Using class imbalance learn-

ing for software defect prediction. IEEE Transactions

on Reliability, 62(2):434–443.

Zheng, J. (2010). Cost-sensitive boosting neural networks

for software defect prediction. Expert Systems with

Applications, 37(6):4537–4543.

Clustering-based Under-sampling for Software Defect Prediction

193