
Mixed Precision Tuning with Salsa
Nasrine Damouche and Matthieu Martel
LAMPS Laboratory, University of Perpignan, France
Keywords:
Mixed Precision, Numerical Accuracy, Program Transformation, Floating-point Arithmetic.
Abstract:
Precision tuning consists of finding the least floating-point formats enabling a program to compute some
results with an accuracy requirement. In mixed precision, this problem has a huge combinatory since any
value may have its own format. Precision tuning has given rise to the development of several tools that aim at
guarantying a desired precision on the outputs of programs doing floating-point computations, by minimizing
the initial, over-estimated, precision of the inputs and intermediary results. In this article, we present an
extension of our tool for numerical accuracy, Salsa, which performs precision tuning. Originally, Salsa is
a program transformation tool based on static analysis and which improves the accuracy of floating-point
computations. We have extended Salsa with a precision tuning static analysis. We present experimental results
showing the efficiency of this new feature as well as the additional gains that we obtain by performing Salsa’s
program transformation before the precision tuning analysis. We experiment our tool on a set of programs
coming from various domains like embedded systems and numerical analysis.
1 INTRODUCTION
Precision tuning consists of finding the least floating-
point formats enabling a program to compute some
results with an accuracy requirement. This problem
has many applications, such as image transmission
protocols from observation satellites to earth as de-
fined by the European Cooperation for Space Stan-
dardization initiative
1
. Precision tuning allows com-
pilers to select the most appropriate formats (for ex-
ample IEEE754 (ANSI/IEEE, 2008) half, single, dou-
ble or quadruple formats (ANSI/IEEE, 2008; Muller
et al., 2010)) for each variable. It is then possible to
save memory, reduce CPU usage and use less band-
width for communications whenever distributed ap-
plications are concerned. So, the choice of the best
floating-point formats is an important compile-time
optimization in many contexts. Precision tuning is
also of great interest for the fixed-point arithmetic for
which it is important to determine data formats, for
example in FPGAs (Gao et al., 2013; Martel et al.,
2014). In mixed precision, i.e. when every variable
or intermediary result may have its own format, pos-
sibly different from the format of the other variables,
this problem has a huge combinatory.
Recently, several approaches and tools have
been proposed for precision tuning, based on dyna-
1
http://ecss.nl/
mic (Lam et al., 2013; Rubio-Gonzalez et al., 2013)
or static (Martel, 2017) analysis. In this article, we
introduce the precision tuning analysis that we have
implemented in Salsa (Damouche et al., 2017a), a
tool dedicated to numerical accuracy. Salsa is an au-
tomatic tool to improve the accuracy of the floating-
point computations done in numerical codes. Based
on static analysis methods by abstract interpretation,
Salsa takes as input an original program, applies to
it a set of transformations and then generates an opti-
mized program which is more accurate than the initial
one. The original and the transformed programs are
written in the same imperative language.
In this article, we are motivated by the need for
an efficient precision with a better accuracy of varia-
bles of programs. Our precision tuning analysis (Mar-
tel, 2017) combines a forward and a backward static
analysis, done by abstract interpretation (Cousot and
Cousot, 1977). We express the forward and backward
analysis as a set of constraints made of propositional
logic formulas and relations between affine expres-
sions over integers (and only integers). These con-
straints can be easily checked by a SMT solver (we
use Z3 in practice (de Moura and Bjørner, 2008)).
We show how we can combine mixed-precision
tuning of floating-point programs with the impro-
vement of the numerical accuracy done by program
transformation in Salsa. The study presented in this
Damouche, N. and Martel, M.
Mixed Precision Tuning with Salsa.
DOI: 10.5220/0006915500470056
In Proceedings of the 8th International Joint Conference on Pervasive and Embedded Computing and Communication Systems (PECCS 2018), pages 47-56
ISBN: 978-989-758-322-3
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
47

article use a benchmark of programs coming from
embedded systems and numerical analysis. We focus
in basic computation bricks such as PID controllers,
matrix-vector product or polynomial evaluation. We
consider several precisions (half, single double pre-
cision (ANSI/IEEE, 2008)), We show that if we ini-
tially set all the variables at a given precision and if
we require that the result of the computation has half
the precision of the inputs (e.g input in double pre-
cision and result in single precision) then our tuning
precision module reduce the format of the inputs by
an average factor of 60% This factor is even impro-
ved if we transform the original program in order to
improve its numerical accuracy. Our experiments also
show that the tuning analysis time is very short which
is important in order to embed it inside a compiler.
In this article, we focus on the accuracy of com-
putations and we omit other problems related to
runtime-errors (Barr et al., 2013; Bertrane et al.,
2011). In particular, overflows are not considered.
In practice, a static analysis computing the ranges of
the variables and rejecting programs which possibly
contain overflows is done before our precision tuning
analysis.
This article is organized as follows. In Section 2,
we give a brief description of the floating-point
arithmetic and we introduce the former work on
mixed-precision. We present in Section 3 the Salsa
tool and the precision tuning analysis implemented
in Salsa. In Section 4, we illustrate our approach
on various programs and then we discuss the results
obtained. Conclusion and future work are given in
Section 5.
2 PRELIMINARY ELEMENTS
In this section we introduce some background mate-
rial. A brief overview of the IEEE754 Standard is
given in Section 2.1 and related work is discussed in
Section 2.2.
2.1 Elements of Floating-point
Arithmetic
We introduce here some elements of floating-point
arithmetic (ANSI/IEEE, 2008; Muller et al., 2010).
First of all, a floating-point number x in base β is de-
fined by
x = s ·(d
0
.d
1
...d
p−1
) · β
e
= s · m · β
e−p+1
(1)
where s ∈ {−1,1} is the sign, m = d
0
d
1
.. . d
p−1
is the
significand, 0 ≤ d
i
< β, 0 ≤ i ≤ p − 1, p is the preci-
sion and e is the exponent, e
min
≤ e ≤ e
max
.
Format Name p e bits e
min
e
max
Binary16 Half prec. 11 5 −14 +15
Binary32 Single prec. 24 8 −126 +127
Binary64 Double prec. 53 11 −1122 +1223
Binary128 Quadruple prec. 113 15 −16382 +16383
Figure 1: Basic binary IEEE754 formats.
A floating-point number x is normalized whene-
ver d
0
6= 0. Normalization avoids multiple repre-
sentations of the same number. The IEEE754 Stan-
dard also defines denormalized numbers which are
floating-point numbers with d
0
= d
1
= . .. = d
k
= 0,
k < p − 1 and e = e
min
. Denormalized numbers make
underflow gradual (Muller et al., 2010). The IEEE754
Standard defines binary formats (with β = 2) and de-
cimal formats (with β = 10). In this article, without
loss of generality, we only consider normalized num-
bers and we always assume that β = 2 (which is the
most common case in practice). The IEEE754 Stan-
dard also specifies a few values for p, e
min
and e
max
which are summarized in Figure 1. Finally, special
values also are defined: nan (Not a Number) resulting
from an invalid operation, ±∞ corresponding to over-
flows, and +0 and −0 (signed zeros).
The IEEE754 Standard also defines five rounding
modes for elementary operations over floating-point
numbers. These modes are towards −∞, towards +∞,
towards zero, to the nearest ties to even and to the ne-
arest ties to away and we write them ◦
−∞
, ◦
+∞
, ◦
0
,
◦
∼
e
and ◦
∼
a
, respectively. The semantics of the ele-
mentary operations ∈ {+, −, ×, ÷} is then defined
by
f
1
◦
f
2
= ◦( f
1
f
2
) (2)
where ◦ ∈ {◦
−∞
,◦
+∞
,◦
0
,◦
∼
e
,◦
∼
a
} denotes the roun-
ding mode. Equation (2) states that the result of a
floating-point operation
◦
done with the rounding
mode ◦ returns what we would obtain by performing
the exact operation and next rounding the result
using ◦. The IEEE754 Standard also specifies how
the square root function must be rounded in a similar
way to Equation (2) but does not specify the roundoff
of other functions like sin, log, etc.
We introduce hereafter two functions which com-
pute the unit in the f irst place and the unit in the last
place of a floating-point number. These functions are
used further in this article to generate constraints en-
coding the way roundoff errors are propagated throug-
hout computations. The ufp of a number x is
ufp(x) = min
i ∈ N : 2
i+1
> x
= blog
2
(x)c . (3)
The ulp of a floating-point number which significand
has size p is defined by
ulp(x) = ufp(x) − p + 1 . (4)
PEC 2018 - International Conference on Pervasive and Embedded Computing
48

The ufp of a floating-point number corresponds to the
binary exponent of its most significant digit. Conver-
sely, the ulp of a floating-point number corresponds
to the binary exponent of its least significant digit.
Note that several definitions of the ulp have been gi-
ven (Muller, 2005).
2.2 Related Work
Several approaches have been proposed to determine
the best floating-point formats as a function of the ex-
pected accuracy on the results. Darulova and Kuncak
use a forward static analysis to compute the propaga-
tion of errors (Darulova and Kuncak, 2014). If the
computed bound on the accuracy satisfies the post-
conditions then the analysis is run again with a smal-
ler format until the best format is found. Note that
in this approach, all the values have the same format
(contrarily to our framework where each control-point
has its own format). While Darulova and Kuncak de-
velop their own static analysis, other static techniques
(Goubault, 2013; Solovyev et al., 2015) could be used
to infer from the forward error propagation the suita-
ble formats. Chiang et al. (Chiang et al., 2017) have
proposed a method to allocate a precision to the terms
of an arithmetic expression (only). They use a for-
mal analysis via Symbolic Taylor Expansions and er-
ror analysis based on interval functions. In spite of
our linear constraints, they solve a quadratically con-
strained quadratic program to obtain annotations.
Other approaches rely on dynamic analysis. For
instance, the Precimonious tool tries to decrease the
precision of variables and checks whether the accu-
racy requirements are still fulfilled (Nguyen et al.,
2016; Rubio-Gonzalez et al., 2013). Lam et al in-
strument binary codes in order to modify their preci-
sion without modifying the source codes (Lam et al.,
2013). They also propose a dynamic search method to
identify the pieces of code where the precision should
be modified.
Finally other work focus on formal methods and
numerical analysis. A first related research direction
concerns formal proofs and the use of proof assistants
to guaranty the accuracy of finite-precision computa-
tions (Boldo et al., 2015; Harrison, 2007; Lee et al.,
2018). Another related research direction concerns
the compile-time optimization of programs in order
to improve the accuracy of the floating-point compu-
tation in function of given ranges for the inputs, wit-
hout modifying the formats of the numbers (Damou-
che et al., 2017a; P. Panchekha and Tatlock, 2015).
3 THE SALSA TOOL
In this section, we introduce our tool, Salsa, for nu-
merical accuracy optimization by program transfor-
mation. Section 3.1 presents the tool in general and,
in Section 3.2, we describe the module dedicated to
precision tuning.
3.1 Overview of Salsa
Salsa is a tool that improves the numerical accu-
racy of programs based on floating-point arithme-
tic (Damouche and Martel, 2017). It reduces partly
the round-off errors by automatically transforming
C-like programs in a source to source manner. We
have defined a set of intraprocedural transformation
rules (Damouche et al., 2016a) like assignments, con-
ditionals, loops, etc., and interprocedural transforma-
tion rules (Damouche et al., 2017b) for functions and
other rules deal with arrays. Salsa relies on static
analysis by abstract interpretation to compute vari-
able ranges and round-off error bounds. It takes as
first input ranges for the input variables of programs
id ∈ [a,b]. These ranges are given by the user or co-
ming from sensors. Salsa takes as second input a
program to be transformed. Salsa applies the requi-
red transformation rules and returns as output a trans-
formed program with better accuracy.
Salsa is composed of several modules. The first
module is the parser that takes the original program
in C-like language with annotations, puts it in SSA
form and then returns its binary syntax tree. The se-
cond module consists in a static analyzer, based on ab-
stract interpretation (Cousot and Cousot, 1977), that
infers safe ranges for the variables and computes er-
rors bounds on them. The third module contains the
intraprocedural transformation rules. The fourth mo-
dule implements the interprocedural transformation
rules. The last module is the Sardana tool, that we
have integrated in our Salsa and call it on arithmetic
expressions in order to improve their numerical accu-
racy.
When transforming programs we build larger
arithmetic expressions that we choose to parse in a
different ways to find a more accurate one. These
large expressions will be sliced at a given level of
the binary syntactic tree and assigned to intermedi-
ary variables named TMP. Note that the transformed
program is semantically different from the original
one but mathematically are equivalent. In (Damou-
che et al., 2017a), we have introduced a proof by in-
duction that demonstrate the correctness of our trans-
formation. In other words, we have proved that the
original and the transformed programs are equivalent.
Mixed Precision Tuning with Salsa
49

kp = 0.194 ;
kd = 0.028 ;
inv d t = 10.0;
m = [ -1.0 ,1 .0] ;
c = 0 .5;
eol d = 0.0 ;
t = 0 .0;
whi l e ( t < 50 0 . 0) {
e = c + (m * ( -1 .0)) ;
p = kp * e;
d = kd * invdt *( e +( eo ld *( - 1.0)) ) ;
r = p + d;
eol d = e ;
t = t + 1.0;
};
req u i r e _ a c c u rac y ( r ,1 1 );
m = [ -1.0 ,1 .0] ;
c = 0 .5;
eol d = 0.0 ;
t = 0 .0;
whi l e ( t < 50 0 . 0) {
e = c + (m * ( -1 .0)) ;
p = (e * 0 . 1 9 4 );
d = (( e * 0.2 8 ) + ( ( - 1 .0)*( eo ld *0.28) ) ) ;
r = (d + p );
eol d = e ;
t = t + 1.0;
};
req u i r e _ a c c u rac y ( r ,1 1 );
Figure 2: Initial (left) and transformed (right) PID Controllers.
For example, Figure 2 gives the initial program of
a PID Controller where all the input variables are de-
clared in single precision and the output variable is
in half precision. We give in Figure 2, the PID Con-
troller program after being transforming by our tool,
Salsa. For readability reasons, in Figure 2, we have
omitted the precision on the inputs and control points
of the programs. For example, when the program is
in single precision, all the control points are initiali-
zed to 24.
3.2 Precision Tuning in Salsa
In this section we introduce our module to determine
the minimal precision on the inputs and on the in-
termediary results of a program performing floating-
point computations in order to ensure a desired accu-
racy on the outputs. Our tool combines a forward and
a backward static analysis, done by abstract interpre-
tation (Cousot and Cousot, 1977). These static analy-
sis are done after the first static analysis which com-
putes the ranges of the values at each control point.
The forward analysis is classical and propagates sa-
fely the errors on the inputs and on the results of
the intermediary operations in order to determine the
accuracy of the results. Next, based on the results
of the forward analysis and on assertions indicating
which accuracy the user wants for the outputs at some
control points, the backward analysis computes the
minimal precision needed for the inputs and interme-
diary results in order to satisfy the assertions.
We express the forward and backward transfer
functions as a set of constraints made of propositi-
onal logic formulas and relations between affine ex-
pressions over integers (and only integers). Indeed,
these relations remain linear even if the analyzed pro-
gram contains non-linear computations. As a conse-
quence, these constraints can be easily checked by
a SMT solver (we use Z3 in practice (Barrett et al.,
2009; de Moura and Bjørner, 2008)). The advantage
of the solver appears in the backward analysis, when
one wants to determine the precision of the operands
of some binary operation between two operands a and
b, in order to obtain a certain accuracy on the result.
In general, it is possible to use a more precise a with
a less precise b or, conversely, to use a more precise
b with a less precise a. Because this choice arises at
almost any operation, there is a huge number of com-
binations on the admissible formats of all the data in
order to ensure a given accuracy on the results.
Example 3.1. For example, let us consider the pro-
gram of Figure 3 which implements a simple linear
filter. At each iteration t of the loop, the output
y
t
is computed as a function of the current input x
t
and of the values x
t−1
and y
t−1
of the former ite-
ration. Our program contains several annotations.
First, the statement require accuracy(y
t
,10)
on the last line of the code informs the system that
the programmer wants to have 10 accurate binary
digits on y
t
at this control point. In other words,
let y
t
= d
0
.d
1
.. . d
n
· 2
e
for some n ≥ 10, the abso-
lute error between the value v that y
t
would have if
all the computations where done with real numbers
and the floating-point value ˆv of y
t
is less than 2
e−11
:
|v − ˆv| ≤ 2
e−9
.
An abstract value [a, b]
p
represents the set of
floating-point values with p accurate bits ranging
from a to b. For example, in the code of Figure
3, the variables x
t−1
and x
t
are initialized to the
abstract value [1.0, 3.0]
16
thanks to the annotation
[1.0,3.0]#16. Let F
p
be the set of all floating-point
numbers with accuracy p. This means that, compared
PEC 2018 - International Conference on Pervasive and Embedded Computing
50

x
t−1
:= [1 .0 ,3. 0] #1 6;
x
t
:= [1 .0 ,3. 0] #1 6;
y
t−1
:= 0. 0;
wh ile ( c) {
u : = 0. 3 * y
t−1
;
v : = 0. 7 * ( x
t
+ x
t−1
);
y
t
:= u + v;
y
t−1
:= y
t
;
};
re q ui re _ ac cu r ac y ( y
t
,10) ;
x
|9|
t−1
:= [1 .0 , 3.0 ]
|9|
; x
|9|
t
:= [1 .0 , 3.0 ]
|9|
;
y
|10|
t−1
:= 0.0
|10|
;
wh ile ( c) {
u
|10|
:= 0.3
|10|
*
|10|
y
|10|
t−1
;
v
|10|
:= 0.7
|11|
*
|10|
( x
|9|
t
+
|10|
x
|9|
t−1
);
y
|10|
t
:= u
|10|
+
|10|
v
|10|
;
y
|10|
t−1
:= y
|10|
t
; } ;
re q ui re _ ac cu r ac y ( y
t
,10) ;
vo la ti le ha lf x
t−1
, x
t
;
ha lf u , v , y
t
;
fl oat y
t−1
, t mp ;
y
t−1
:= 0. 0;
wh ile ( c) {
u : = 0. 3 * y
t−1
;
tmp := x
t
+ x
t−1
;
v : = 0. 7 * t mp ;
y
t
:= u + v;
y
t−1
:= y
t
;
};
x
|16|
t−1
:= [1 .0 , 3.0 ]
|16|
;
x
|16|
t
:= [1 .0 , 3.0 ]
|16|
;
y
|52|
t−1
:= 0.0
|52|
;
u
|52|
:= 0.3
|52|
*
|52|
y
|52|
t−1
;
v
|15|
:= 0.7
|52|
*
|15|
( x
|16|
t
+
|16|
x
|16|
t−1
);
y
|15|
t
:= u
|52|
+
|15|
v
|15|
;
y
|15|
t−1
:= y
|15|
t
;
x
|9|
t−1
:= [1 .0 , 3.0 ]
|9|
; x
|9|
t
:= [1 .0 , 3.0 ]
|9|
;
y
|8|
t−1
:= 0.0
|8|
;
u
|10|
:= 0.3
|8|
*
|10|
y
|8|
t−1
;
v
|10|
:= 0.7
|11|
*
|10|
( x
|9|
t
+
|10|
x
|9|
t−1
);
y
|10|
t
:= u
|10|
+
|10|
v
|10|
;
y
|10|
t−1
:= y
|10|
t
;
re q ui re _ ac cu r ac y ( y
t
,10) ;
Figure 3: Top left: Initial program. Top middle: Annotations after analysis. Top right: Final program with generated data
types Bottom left: Forward analysis (one iteration). Bottom middle: Backward analysis (one iteration).
to exact value v computed in infinite precision, the
value ˆv = d
0
.d
1
.. . d
n
· 2
e
of F
p
is such that |v − ˆv| ≤
2
e−p+1
. By definition, using the function ufp introdu-
ced in Equation (3), for any x ∈ F
p
the roundoff error
ε(x) on x is bounded by ε(x) < 2
ulp(x)
= 2
ufp(x)−p+1
.
Concerning the abstract values, intuitively we have
the concretization function
γ([a,b]
p
) = {x ∈ F
p
: a ≤ x ≤ b} . (5)
In our example, x
t
and x
t−1
belong to [1.0, 3.0]
16
which means, by definition, that these variables have
a value ˆv ranging in [1.0, 3.0] and such that the error
between ˆv and the value v that we would have in the
exact arithmetic is bounded by 2
ufp(x)−15
. Typically,
in this example, this information would come from
the specification of the sensor related to x. By default,
the values for which no accuracy annotation is given
(for instance the value of y
t−1
in the example of
Figure 3) are considered as exact numbers rounded
to the nearest in double precision. In this format
numbers have 53 bits of significand (see Figure 1).
The last bit being rounded, these numbers have 52
accurate bits in our terminology and, consequently,
by default values belong to F
52
in our framework.
Based on the accuracy of the inputs, our forward
analysis computes the accuracy of all the other varia-
bles and expressions. The program in the left bottom
corner of Figure 3 displays the result of the forward
analysis on the first iteration of the loop. Let
→
⊕ denote
the forward addition, the result of x
t
+x
t−1
has 16
accurate digits since
→
⊕(1.0#16,1.0#16) = 2.0#16,
→
⊕(1.0#16,3.0#16) = 4.0#17,
→
⊕(3.0#16,1.0#16) =
4.0#17,
→
⊕(3.0#16,3.0#16) = 6.0#16.
→
([1.0,3.0]#16, [1.0, 3.0]#16) = [2.0, 6.0]#16.
The backward analysis is performed after the for-
ward analysis and takes advantage of the accuracy re-
quirement at the end of the code (see the right bottom
corner of Figure 3 for an unfolding of the backward
analysis on the first iteration of the loop). Since, in
our example, 10 bits only are required for y
t
, the re-
sult of the addition u+v also needs 10 accurate bits
only. By combining this information with the result
of the forward analysis, it is then possible to lower
the number of bits needed for one of the operands.
Let
←
⊕ be the backward addition.
Example 3.2. For example, for x
t
+x
t−1
in the as-
signment of v, we have
←
⊕(2.0#10,1.0#16) = 1.0#8,
←
⊕(2.0#10,3.0#16) = −1.0#8,
←
⊕(6.0#10,1.0#16) =
5.0#9,
←
⊕(6.0#10,3.0#16) = 3.0#8.
Conversely to the forward function, the interval
function now keeps the largest accuracy arising in the
computation of the bounds:
←
([2.0,6.0]#10, [1.0, 3.0]#16) = [1.0, 3.0]#9 .
By processing similarly on all the elementary ope-
rations and after computation of the loop fixed point,
we obtain the final result of the analysis displayed in
the top right corner of Figure 3. This information may
be used to determine the most appropriate data type
for each variable and operation, as shown in Figure 3.
To obtain this result we generate a set of constraints
corresponding to the forward and backward transfer
Mixed Precision Tuning with Salsa
51

functions for the operations of the program. There
exist several ways to handle a backward operation:
when the accuracy on the inputs x and y computed
by the forward analysis is too large wrt. the desired
accuracy on the result, one may lower the accuracy of
either x or y or both. Since this question arises at each
binary operation, we would face to a huge number of
combinations if we decided to enumerate all possibili-
ties. Instead, we generate a disjunction of constraints
corresponding to the minimization of the accuracy of
each operand and we let the solver search for a solu-
tion. The control flow of the program is also enco-
ded with constraints. For a sequence of statements,
we relate the accuracy of the former statements to the
accuracy of the latter ones. Each variable x has three
parameters: its forward, backward and final accuracy,
denoted acc
F
(x), acc
B
(x) and acc(x) respectively. We
must always have
0 ≤ acc
B
(x) ≤ acc(x) ≤ acc
F
(x) . (6)
For the forward analysis, the accuracy of some va-
riable may decrease when passing to the next state-
ment (we may only weaken the pre-conditions). Con-
versely, in the backward analysis, the accuracy of a gi-
ven variable may increase when we jump to a former
statement in the control graph (the post-conditions
may only be strengthened). For a loop, we relate the
accuracy of the variables at the beginning and at the
end of the body, in a standard way.
The key point of our technique is to generate sim-
ple constraints made of propositional logic formu-
las and of affine expressions among integers (even if
the floating-point computations in the source code are
non-linear). A static analysis computing safe ranges
at each control point is performed before our accuracy
analysis. Then the constraints depend on two kinds
of integer parameters: the ufp of the values and their
accuracies acc
F
, acc
B
and acc. For instance, given
control points `
1
, `
2
and `
3
, the set C of constraints
generated for 3.0#16
`
1
+
`
3
1.0#16
`
2
, assuming that
we require 10 accurate bits for the result are:
C =
acc
F
(`
1
) = 16, acc
F
(`
2
) = 16,
r
`
3
= 2 − max(acc
F
(`
1
) − 1, acc
F
(`
2
)),
(1 − acc
F
(`
1
)) = acc
F
(`
2
) ⇒ i
`
3
= 1,
(1 − acc
F
(`
1
)) 6= acc
F
(`
2
) ⇒ i
`
3
= 0,
acc
F
(`
3
) = r
`
3
− i
`
3
, acc
B
(`
3
) = 10
acc
B
(`
1
) = 1 −(2 − acc
B
(`
3
)),
acc
B
(`
2
) = 1 −(2 − acc
B
(`
3
))
.
For the sake of conciseness, the constraints corre-
sponding to Equation (6) have been omitted in C.
For example, for the forward addition, the accuracy
acc
F
(`
3
) of the result is the number of bits between
ufp(3.0 + 1.0) = 2 and the ufp u of the error which is
u = max
ufp(3.0) − acc
F
(`
1
),ufp(1.0) − acc
F
(`
2
)
+ i
= max
1 − acc
F
(`
1
),0 − acc
F
(`
2
)
+ i ,
where i = 0 or i = 1 depending on some condition
detailed later. The constraints generated for each kind
of expression and command are detailed in (Martel,
2017).
4 EXPERIMENTS
In this section, we illustrate the usefulness of our
techniques by its application to various programs co-
ming from embedded systems and numerical analy-
sis. We start by giving a brief description of each
program considered. Then, we show and discuss the
result obtained using our techniques.
• PID Controller: This program implements a
controller which aims at maintaining a physical
parameter at a specific value known as the set-
point (Damouche et al., 2017a) (see Figure 2),
• Odometry: This program consists of computing
the position (x,y) of a two wheeled robots by odo-
metry (Damouche et al., 2017a), i.e., from the ini-
tial position and from the speed of the wheels,
• Linear Filter: This program implements a li-
near filter in which the value of an output signal
is a linear combination of the values of the input
sampled signal at the last instants (see Figure 3),
• Linear Regression: This program implements
linear regression, a technique for modeling the re-
lationship between a scalar dependent variable y
and one or more independent variables denoted X,
• Horner: This program implements a polynomial
evaluation method and is applied to a polynomial
of degree 9 (Martel, 2017),
• FPTaylor: This program corrects sensor data in
control software, where the output of the sen-
sor is known to be between 1.001 and 2.0 by
using Taylor series to narrow the computed error
bounds (Damouche et al., 2016b; Solovyev et al.,
2015),
• Taylor Series: This program implements the
function
1
1−x
using Taylor’s series.
• Determinant: This program computes the de-
terminant Det(M) of a 3 × 3 matrix M (Martel,
2017),
• MatVectMul: This program computes a 3 × 3 ma-
trix vector product,
• MatMatMul: This program computes a 3 × 3 ma-
trix matrix product.
Figures 4, 5 and 6 summarize the results obtained
for finding a minimal floating-point formats by ensu-
PEC 2018 - International Conference on Pervasive and Embedded Computing
52

Initial #nbCPT Initial Prec. Tun. Improvement Prec. Tun. Improvement
Code #nbCP after trans. prec. of prog. % with Salsa %
PID Controller 42 34 1008 381 62.2 282 72.0
Odometry 68 70 1632 486 70.2 437 73.2
Linear Filter 30 24 720 278 61.3 255 64.5
Linear Regression 44 28 1056 585 55.4 365 65.4
Horner 16 16 384 166 56.7 166 56.7
FPTaylor 18 20 432 243 43.7 - -
Taylor Series 22 22 528 188 64.4 155 70.6
Determinant 72 60 1728 547 68.3 443 74.3
MatVectMul 160 160 3840 1570 59.1 1570 59.1
MatMatMul 200 200 4800 1990 58.5 1990 58.5
Figure 4: Measurements of the improvement of the required precision of programs in single precision.
Initial #nbCPT Initial Prec. Tun. Improvement Prec. Tun. Improvement
Code #nbCP after trans. prec. of prog. % with Salsa %
PID Controller 42 34 2226 914 58.9 659 70.4
Odometry 68 70 3604 1136 68.4 996 72.3
Linear Filter 30 24 1590 616 61.2 567 64.3
Linear Regression 44 22 2332 1157 50.4 703 69.8
Horner 16 16 848 316 57.4 316 57.4
FPTaylor 18 20 954 477 50.0 - -
Taylor Series 22 22 1166 409 64.9 337 71.1
Determinant 72 60 3816 1483 61.1 1223 67.9
MatVectMul 160 160 8480 3650 56.9 3650 56.9
MatMatMul 200 200 10600 4486 57.6 4486 57.6
Figure 5: Measurements of the improvement of the required precision of programs in double precision.
ring a desired accuracy on the outputs. In our experi-
ments, we observe two sides for each program:
• The first side concerns the computation of the
number of control points of each program when
just using the precision tuning analysis (#nbCP)
and then by transforming it and applying the
mixed precision analysis using Salsa (#nbCPT).
• The Second side consists of measuring the pre-
cision on the output of programs when using the
precision tuning analysis (Prog. Prec. Tun.) and
then by using Salsa (Salsa Prec. Tun.).
Note that these experiments have been performed on
three different precision. More precisely, we have de-
clared all the input variables of programs in single,
double and quadruple precision and we have fixed the
desired accuracy of the outputs of programs in half,
single and double precision, respectively.
For instance, if we take the PID Controller exam-
ple given in Figure 4, we initially have a precision
of 1008 bits (Initial Prec.). This number is obtai-
ned by multiplying the number of control points of
the program by the precision associated to its inputs.
In this case, 1008 corresponds to 42 multiplied by
24 bits (single precision). The initial precision of the
PID controller is reduced to 381 bits using only pre-
cision tuning analysis (Prog. Prec. Tun.) and to 282
bits while using Salsa (Salsa Prec. Tun.). The per-
centage of improvement is passed from to 62.2% to
72.0%. In addition, by transforming programs with
Salsa, the number of control points is generally de-
creased. In the case of the PID program, this num-
ber passed from 42 control points (#nbCP) to 34
(#nbCPT). This reduction is mainly done because of
the transformation applied when using Salsa. Note
that, our tuning precision techniques reduces the for-
mat of the inputs by an average factor of 60%. Re-
mark that for the FPTaylor example, our tool has fai-
led to solve it. This is why, we represent it with -.
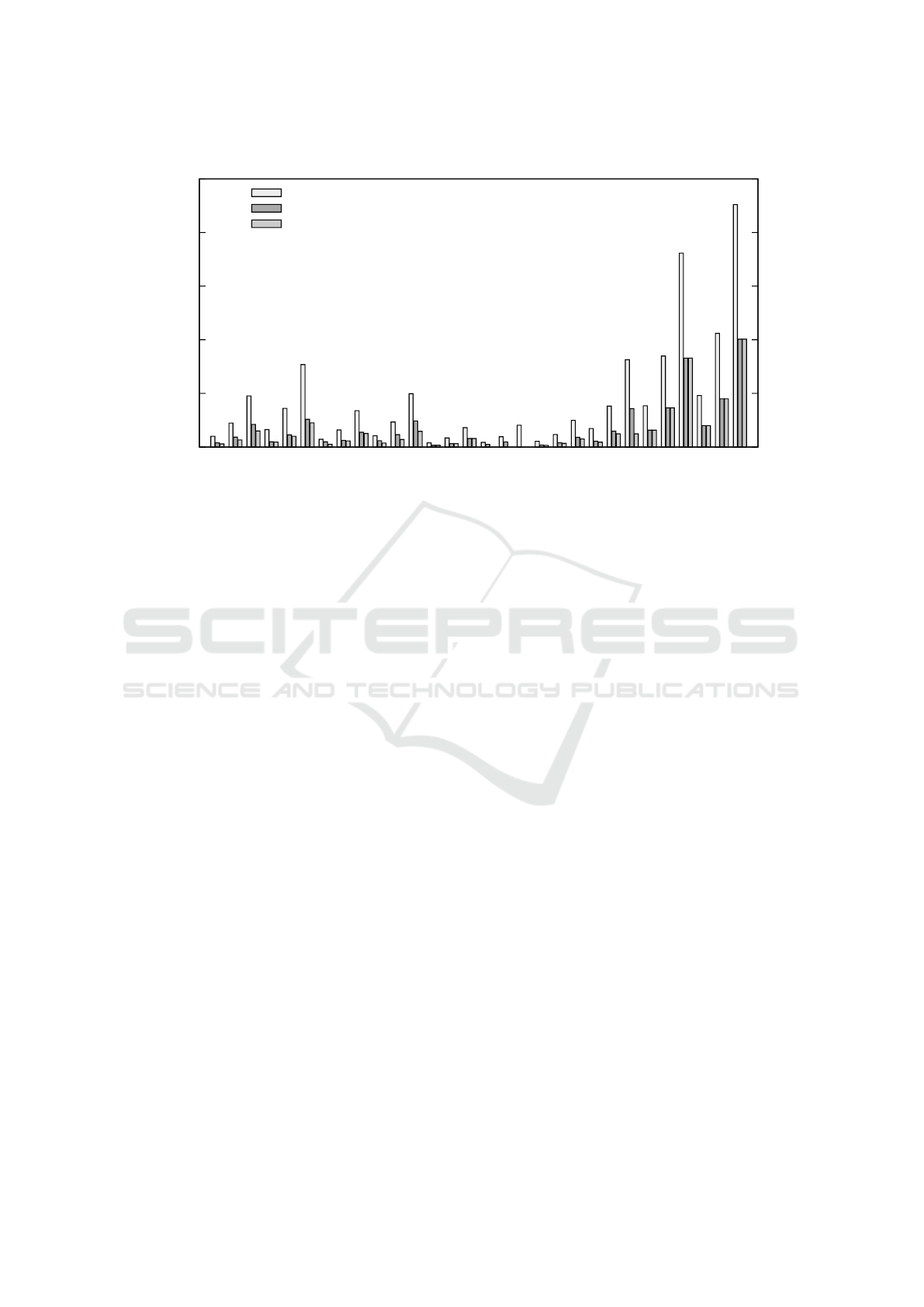
Figure 8 compares the different results obtained
with our techniques. It synthesizes the results of figu-
res 4 to 6. We have drawn the values of the precision
corresponding to the initial program, to the program
using only tuning analysis and to the program trans-
formed by Salsa and this for the different programs
formats. More precisely, Figure 8 gives a comparison
between all the considered programs in single, dou-
ble and quadruple precision respectively correspon-
ding to program24, program53 and program113 on
the x-axis of Figure 8. The results show that for most
programs, we have that when using our tuning ana-
lysis, the precision is reduced by more than 50% like
the PID controller, odometry, filter, linear regression,
etc. In general, we remark that by applying Salsa,
Mixed Precision Tuning with Salsa
53
Initial #nbCPT Initial Prec. Tun. Improvement Prec. Tun. Improvement
Code #nbCP after trans. prec. of prog. % with Salsa %
PID Controller 42 34 4764 2103 55.6 1500 68.3
Odometry 68 70 7684 2586 66.3 2243 70.8
Linear Filter 30 24 3390 1370 59.5 1263 62.7
Linear Regression 44 28 4972 2433 51.0 1457 70.7
Horner 16 16 1808 796 55.9 796 55.9
FPTaylor 18 20 2034 - - - -
Taylor Series 22 22 2486 902 63.7 743 70.1
Determinant 72 60 8136 3571 56.1 1223 84.9
MatVectMul 160 160 18080 8290 54.1 8290 54.1
MatMatMul 200 200 22600 10054 55.5 10054 55.5
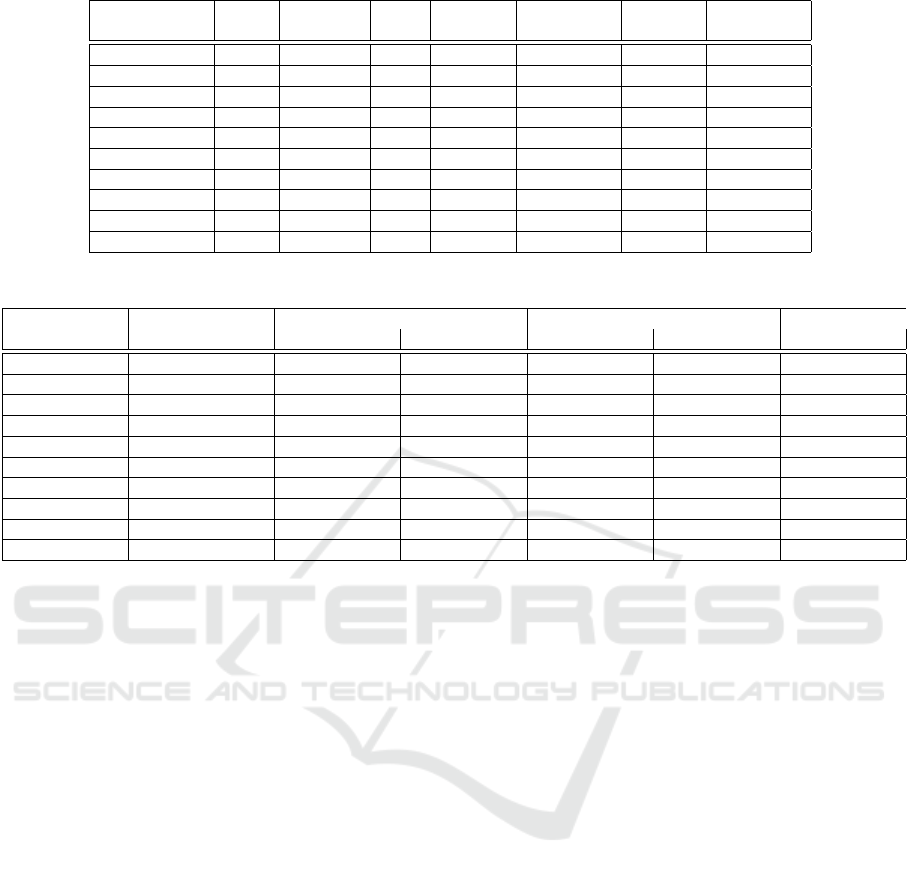
Figure 6: Measurements of the improvement of the required precision of programs in quadruple precision.
Single Prec. (24 bits) Double Prec. (53 bits) Quad. Prec (113 bits)
Code Prog. Exec. Time Salsa Exec. Time Prog. Exec. Time Salsa Exec. Time Prog. Exec. Time Salsa Exec. Time
PID Controller 0.060 0.048 0.056 0.040 0.044 0.028
Odometry 0.048 0.032 0.044 0.036 0.036 0.032
Linear Filter 0.028 0.024 0.032 0.028 0.036 0.028
Linear Regression 0.028 0.024 0.036 0.024 0.036 0.024
Horner 0.024 0.020 0.032 0.032 0.028 0.016
FPTaylor 0.020 0.016 0.036 0.032 0.040 0.036
Taylor Series 0.024 0.024 0.032 0.028 0.036 0.028
Determinant 0.052 0.036 0.044 0.040 0.052 0.048
MatVectMul 0.068 0.056 0.052 0.040 0.068 0.064
MatMatMul 0.072 0.056 0.080 0.068 0.068 0.052
Figure 7: Execution time measurements of programs.
the precision of programs is improved by an average
of about 10 additional percents compared to the di-
rect tuning analysis. Otherwise, in some cases, like
the program that computes the matrix vector product,
or the matrix matrix product, there is no more impro-
vement. These results are very representative since it
allows to decrease widely the precision of programs.
It will be more interesting if we could improve even
more the accuracy of programs by finding new techni-
ques and strategies. Indeed, in future work we plan
to improve Salsa for this situation by modifying our
program transformation in order to favor the precision
tuning analysis and not only the accuracy during the
rewriting of the expressions.
In the other side, we have measured the execution
time of programs. More precisely, for each program,
we measure the execution time required by the the
program performing just the precision tuning analysis
(Prog. Exec. Time) and then when applying Salsa
(Salsa Exec. Time ) and this for single, double and
quadruple precision. Figure 7 summarized the dif-
ferent results obtained. For instance, if we consider
the PID Controller program, it takes 0.060 seconds
for execution when using the precision tuning analy-
sis while it takes 0.048 seconds when applying Salsa.
For the other programs, the execution time is almost
always improved.
These results shown the efficiency and the useful-
ness of our techniques on saving memory space, redu-
cing the CPU usage, decreasing the bandwidth usage
and reducing the execution time of each program.
5 CONCLUSION
In this article, we have studied how to find an effi-
cient precision with a better accuracy of variables of
programs. The originality of the idea is to improve
the numerical accuracy, by using our tool Salsa, and
simultaneously minimize the precision on the outputs
of variables of programs using precision tuning analy-
sis. We have experimented our techniques to optimize
the precision and the numerical accuracy programs at
once. The experiments shown that the precision of
the programs has been minimized by an average fac-
tor of 60%. Also, we have shown that by optimizing
the precision and the accuracy, the execution time of
programs is improved.
In our future work, it would be interesting to ex-
tend our techniques to design efficient heuristic refi-
nement that automatically determines and specifies a
least format and a precise range of precision for each
variable of the program. This allows one to further
reduce the used memory space, CPU and bandwidth.
PEC 2018 - International Conference on Pervasive and Embedded Computing
54
0
5000
10000
15000
20000
25000
PID24
PID53
PID113
Odo24
Odo53
Odo113
Filter24
Filter53
Filter113
Reg24
Reg53
Reg113
Horner24
Horner53
Horner113
FPTay24
FPTay53
FPTay113
Series24
Series53
Series113
Det24
Det53
Det113
MatVec24
MatVec53
MatVec113
MatMat24
MatMat53
MatMat113
Quadruple precision
Initial
Mixed
Salsa
Figure 8: Improvements of the required precision of programs in single, double and quadruple precision.
Another perspective is to apply our techniques to
other languages used for the design of critical embed-
ded systems. In particular, it would be of great interest
to have such a type system inside a language used to
build critical embedded systems such as the synchro-
nous language Lustre (Caspi et al., 1987). In this
context numerical accuracy requirements are strong
and difficult to obtain.
REFERENCES
ANSI/IEEE (2008). IEEE Standard for Binary Floating-
Point Arithmetic. SIAM.
Barr, E. T., Vo, T., Le, V., and Su, Z. (2013). Automatic
detection of floating-point exceptions. In POPL ’13,
pages 549–560. ACM.
Barrett, C. W., Sebastiani, R., Seshia, S. A., and Tinelli,
C. (2009). Satisfiability modulo theories. In Hand-
book of Satisfiability, volume 185 of Frontiers in Ar-
tificial Intelligence and Applications, pages 825–885.
IOS Press.
Bertrane, J., Cousot, P., Cousot, R., Feret, J., Mauborgne,
L., Min
´
e, A., and Rival, X. (2011). Static analysis by
abstract interpretation of embedded critical software.
ACM SIGSOFT Software Engineering Notes, 36(1):1–
8.
Boldo, S., Jourdan, J., Leroy, X., and Melquiond, G. (2015).
Verified compilation of floating-point computations.
J. Autom. Reasoning, 54(2):135–163.
Caspi, P., Pilaud, D., Halbwachs, N., and Plaice, J. (1987).
Lustre: A declarative language for programming syn-
chronous systems. In ACM Symposium on Principles
of Programming Languages, pages 178–188. ACM
Press.
Chiang, W., Baranowski, M., Briggs, I., Solovyev, A., Go-
palakrishnan, G., and Rakamaric, Z. (2017). Rigorous
floating-point mixed-precision tuning. In POPL, pa-
ges 300–315. ACM.
Cousot, P. and Cousot, R. (1977). Abstract interpretation: A
unified lattice model for static analysis of programs by
construction or approximation of fixpoints. In Princi-
ples of Programming Languages, pages 238–252.
Damouche, N. and Martel, M. (2017). Salsa : An automa-
tic tool improve the accuracy of programs. In 6th In-
ternational Workshop on Automated Formal Methods,
AFM.
Damouche, N., Martel, M., and Chapoutot, A. (2016a).
Data-types optimization for floating-point formats by
program transformation. In International Conference
on Control, Decision and Information Technologies,
CoDIT 2016, Saint Julian’s, Malta, April 6-8, 2016,
pages 576–581.
Damouche, N., Martel, M., and Chapoutot, A. (2017a). Im-
proving the numerical accuracy of programs by auto-
matic transformation. STTT, 19(4):427–448.
Damouche, N., Martel, M., and Chapoutot, A. (2017b).
Numerical accuracy improvement by interprocedural
program transformation. In Stuijk, S., editor, Procee-
dings of the 20th International Workshop on Software
and Compilers for Embedded Systems, SCOPES 2017,
Sankt Goar, Germany, June 12-13, 2017, pages 1–10.
ACM.
Damouche, N., Martel, M., Panchekha, P., Qiu, C.,
Sanchez-Stern, A., and Tatlock, Z. (2016b). Toward
a standard benchmark format and suite for floating-
point analysis. In S. Bogomolov, M. Martel, P. P., edi-
tor, NSV, LNCS. Springer.
Darulova, E. and Kuncak, V. (2014). Sound compilation
Mixed Precision Tuning with Salsa
55

of reals. In Jagannathan, S. and Sewell, P., editors,
POPL’14, pages 235–248. ACM.
de Moura, L. M. and Bjørner, N. (2008). Z3: an efficient
SMT solver. In TACAS, volume 4963 of LNCS, pages
337–340. Springer.
Gao, X., Bayliss, S., and Constantinides, G. A. (2013).
SOAP: structural optimization of arithmetic expressi-
ons for high-level synthesis. In International Con-
ference on Field-Programmable Technology, pages
112–119. IEEE.
Goubault, E. (2013). Static analysis by abstract interpreta-
tion of numerical programs and systems, and FLUC-
TUAT. In SAS, volume 7935 of LNCS, pages 1–3.
Springer.
Harrison, J. (2007). Floating-point verification. J. UCS,
13(5):629–638.
Lam, M. O., Hollingsworth, J. K., de Supinski, B. R.,
and LeGendre, M. P. (2013). Automatically adapting
programs for mixed-precision floating-point compu-
tation. In Supercomputing, ICS’13, pages 369–378.
ACM.
Lee, W., Sharma, R., and Aiken, A. (2018). On automati-
cally proving the correctness of math.h implementati-
ons. PACMPL, 2(POPL):47:1–47:32.
Martel, M. (2017). Floating-point format inference in
mixed-precision. In Barrett, C., Davies, M., and Ka-
hsai, T., editors, NASA Formal Methods - 9th Interna-
tional Symposium, NFM 2017, volume 10227 of Lec-
ture Notes in Computer Science, pages 230–246.
Martel, M., Najahi, A., and Revy, G. (2014). Code size
and accuracy-aware synthesis of fixed-point programs
for matrix multiplication. In Pervasive and Embedded
Computing and Communication Systems, pages 204–
214. SciTePress.
Muller, J.-M. (2005). On the definition of ulp(x). Technical
Report 2005-09, Laboratoire d’Informatique du Pa-
rall
´
elisme, Ecole Normale Sup
´
erieure de Lyon.
Muller, J.-M., Brisebarre, N., de Dinechin, F., Jeannerod,
C.-P., Lef
`
evre, V., Melquiond, G., Revol, N., Stehl
´
e,
D., and Torres, S. (2010). Handbook of Floating-Point
Arithmetic. Birkh
¨
auser Boston.
Nguyen, C., Rubio-Gonzalez, C., Mehne, B., Sen, K., Dem-
mel, J., Kahan, W., Iancu, C., Lavrijsen, W., Bailey,
D. H., and Hough, D. (2016). Floating-point precision
tuning using blame analysis. In Int. Conf. on Software
Engineering (ICSE). ACM.
P. Panchekha, A. Sanchez-Stern, J. R. W. and Tatlock, Z.
(2015). Automatically improving accuracy for flo-
ating point expressions. In PLDI’15, pages 1–11.
ACM.
Rubio-Gonzalez, C., Nguyen, C., Nguyen, H. D., Demmel,
J., Kahan, W., Sen, K., Bailey, D. H., Iancu, C., and
Hough, D. (2013). Precimonious: tuning assistant for
floating-point precision. In Int. Conf. for High Perfor-
mance Computing, Networking, Storage and Analysis,
pages 27:1–27:12. ACM.
Solovyev, A., Jacobsen, C., Rakamaric, Z., and Gopala-
krishnan, G. (2015). Rigorous estimation of floating-
point round-off errors with symbolic taylor expansi-
ons. In FM’15, volume 9109 of LNCS, pages 532–
550. Springer.
PEC 2018 - International Conference on Pervasive and Embedded Computing
56
