Traversal-aware Encryption Adjustment for Graph Databases

Nahla Aburawi, Frans Coenen and Alexei Lisitsa

Department of Computer Science, University of Liverpool, U.K.

Keywords:

Graph Databases, CryptDB, Encryption Adjustment, Security.

Abstract:

Data processing methods allowing to query encrypted data, such as CryptDB (Popa et al., 2011a) utilize multi-

layered encryption and encryption adjustment in order to provide a reasonable trade-off between data security

protection and data processing efﬁciency. In this paper, we consider querying of encrypted graph databases

and propose a novel traversal-aware encryption adjustment scheme which trades efﬁciency for security. We

show that by dynamically adjusting encryption layers as query execution progresses, we can correctly execute

the query on the encrypted graph store revealing less information to the adversary than in the case of static

adjustment done prior to execution.

1 INTRODUCTION

Data processing methods allowing to query encryp-

ted data, such as CryptDB (Popa et al., 2011a) pro-

vide a powerful mechanism for security protection of

data against server based attacks. In order to pro-

vide a reasonable trade-off between data security pro-

tection and data processing efﬁciency CryptDB uti-

lizes multi-layered encryption and encryption adjus-

tment. Multi-layered encryption allows to control to

some extent the release of information about data ele-

ments required for a query execution. Highest le-

vel of protection can be achieved by the application

of random layer of encryption (RND), meaning that

even equal elements become different after encryp-

tion. However, if the query execution over encrypted

data requires equality checks this cannot be done at

random layer of encryption. In this case the encryp-

tion level should be adjusted prior to the query exe-

cution to the deterministic layer (DET) which allows

for equality checks, but reveal no more information.

In the original CryptDB approach several layers of

different types of encryption organized into encryp-

tion onions have been considered alongside of SQL-

aware encryption schemes, which revealed the neces-

sary information to execute the various types of SQL-

queries, still keeping data itself hidden. One particu-

lar challenge was to support join operations and that

required introduction of a new cryptographic primi-

tive.

In (Aburawi et al., 2018) a variant of CryptDB-

like mechanism for graph databases has been propo-

sed based on an original idea of relational CryptDB

(Popa et al., 2011a). Graph databases have recently

become very popular. The graph structures with no-

des representing entities and edges representing va-

rious connections between these entities constitute a

convenient data model allowing to model all kinds

of scenarios. Querying graph databases may also be

more efﬁcient as compared with relational databases,

especially by data traversal queries. Several imple-

mentations of graph DBMS are available, including

GraphDB, Neo4j, OrientDB, to name a few (Finley,

2011). In a work reported here Neo4j has been used,

a Java-based open source implementation that provi-

des persistence and high performance (neo4j, 2015).

The query language that can be used to access data

in Neo4j is Cypher, which is a declarative language

capable to express the patterns of nodes and relati-

onships in the graph to be matched during the query

execution (Cypher, 2015).

The application of CryptDB principles in the con-

text of graph databases brings challenges with the en-

cryption layer adjustment similar to that of the origi-

nal CryptDB. The fundamental characteristic of en-

cryption adjustment is a selection of an appropriate

encryption layer that reveals an information about an

encrypted data that is needed for executing the query,

but it does not reveal more information about the data

than required. For example, for relational databases,

it has been noticed in (Popa et al., 2011a) that there

is a possibility to leak some unnecessary information

(cross-column equalities) when applying DET layer

during the execution of Join operator. A new Join-

aware encryption scheme has been proposed to solve

this issue (Popa et al., 2011a). In graph databases

Aburawi, N., Coenen, F. and Lisitsa, A.

Traversal-aware Encryption Adjustment for Graph Databases.

DOI: 10.5220/0006916403810387

In Proceedings of the 7th International Conference on Data Science, Technology and Applications (DATA 2018), pages 381-387

ISBN: 978-989-758-318-6

381

no need to perform join (Robinson et al., 2013) and

it is absent in the Cypher query language (Cypher,

2015). Nevertheless, as it was noticed in (Aburawi

et al., 2018) the issue of unnecessary leaks remains

for graph databases as well.

In this paper, we propose a novel encryption ad-

justment scheme which we call ”traversal-aware”.

This scheme, when applied to graph database que-

rying lead to demonstrably less unnecessary leaks of

information. The scheme is dynamic and the encryp-

tion layer adjustment happens not before the query

execution, but rather it gradually progresses alongs-

ide the execution.

This paper is organized as follows, in Section 2

the encryption layers and adjustment as proposed in

(Aburawi et al., 2018) is presented. Section 3 then ex-

plains the CryptGraphDB. The next section, Section

4, presents the proposed traversal-aware encryption

adjustment for graph database. Some conclusions and

some suggested areas for future work are drawn in the

ﬁnal section.

2 ENCRYPTION LAYERS AND

ADJUSTMENT

In this section we outline brieﬂy the concepts of en-

cryption layers and encryption adjustment in the con-

text of encrypted databases querying. Onion Layers

of Encryption considered in (Popa et al., 2011a; Abu-

rawi et al., 2018) allow to change data encryption le-

vels on demand in an efﬁcient way. The main idea

is to encrypt each data item in one or more onions,

where each layer of each onion enables some kinds of

functionality as explained in (Popa et al., 2011a; Abu-

rawi et al., 2018). At the beginning, each data item in

the database is encrypted in all onions of encryption,

started with the most secure encryption scheme as ou-

termost layers. At this point, the server can know no-

thing about the data other than the number of nodes,

properties, and data size, whilst the inner layers such

as OPE and DET provide more functionality. De-

pending on the requirements of a particular query for

data access the level of encryption is adjusted before

query execution. Different cryptographic algorithms

are available to be cascaded into onion layers (as ori-

ginally mention in (Popa et al., 2011a)):

• Random (RND). RND is a probabilistic scheme

that provides the maximum security, when two

equal values are encrypted to different ciphertexts.

RND does not reveal any information on the plain

text and does not allow any computation over the

ciphertext.

• Homomorphic encryption (HOM). HOM is a

method of encryption that allows to perform cal-

culations on encrypted information without de-

crypting it ﬁrst.

• Deterministic (DET). DET generates the same

ciphertext that correspond to the same plaintext,

DET was implemented to let the equality checks

to be performed.

• Order-preserving encryption (OPE). OPE is a

scheme that produces ciphertexts that preserve the

order of their plaintexts, and allows to perform

comparisons between data values based on their

encrypted versions.

• Word search (SEARCH). SEARCH allows to

execute searches on encrypted text.

3 CryptGraphDB

In (Aburawi et al., 2018) a proposed approach for

graph database inspired by CryptDB was reported

whereby executing a cypher query over an encrypted

graph database as if it was executed over a plain graph

database. Therefore, the typical processing of a query

in CryptGraphDB can be performed as follows:

1. The application issues a query, which is rewritten

and anonymizes each label, node, and relations-

hip name, and encrypts each constant in the query

with an encryption scheme that allows the requi-

red operation.

2. By using multi-layered encryption and encryp-

tion, adjust encryption layers before executing the

query if DBMS needs to do. If so, issues an UP-

DATE query to adjust the encryption layer of the

appropriate node, while the semantics of the query

are preserved.

3. The encrypted query is sent to the DBMS server to

be executed by using standard Cypher and return

the encrypted results.

4. The server returns the encrypted result of the

query, then the proxy decrypts and returns to the

application.

To illustrate how CryptGraphDB processes the

cypher query, consider an example scenario as can be

seen in Figure 1, consisting of a graph database la-

bel Person, which has ten nodes of interest: name

and age as properties. Initially, each property in this

graph database is adapted in onion of encryption with

RND as outermost layer. At this stage, the server (or

rather an attacker taken over the server, or curious ad-

ministrator) can recognize nothing about the data con-

DATA 2018 - 7th International Conference on Data Science, Technology and Applications

382

tent other than the number of nodes, properties, and

relationships.

To illustrate the adjustment of the onion layers the

following query is considered:

MATCH (A:person)-[:Knows]->(person)

WHERE A.name = "Tom"

RETURN person

In this query an adjustment for name is re-

quired to level DET. Accordingly, an update

query is needed to UPDATE Label:person to

person1 by decrypting the name property to

DET layer, UPDATE person1 SET P-Onion =

DECRYPT-RND( P-Onion). DBMS decrypts en-

tire name property to DET layer. Then, execute the

encrypted query:

MATCH (A:person1)-[:Knows1]->(person1)

WHERE A.name1 = "D1"

RETURN person1

Where D1 is an encryption of Tom. The outcome

of this query will be X77, X33, and X88 as the

encrypted RND of Smith, Smith, and Lee, re-

spectively. The encrypted results are returned to the

user; they can be decrypted in transit by a proxy.

In this way CryptGraphDB, similarly to CryptDB

could use various encryption schemes that support se-

veral operations, such as check the equality , order

comparisons and some arithmetic calculations. As en-

cryption layer adjustment concerned, in both, original

CryptDB and CryptGraphDB it happens before query

execution. It has noticeable consequences in the con-

text of CryptGraphDB. The required adjustment is

performed everywhere in the database instance. So,

for example, if the query requires access to equality

of values for any property, the encryption layers for

this property values are adjusted in all nodes where

the property is present. As we will see that may lead

to unnecessary information leaks. In the next section

we present an approach which allows to reveal less in-

formation when performing an encryption adjustment

at least for some types of queries.

4 TRAVERSAL-AWARE

ENCRYPTION ADJUSTMENT

The idea of traversal-aware encryption adjustment is

quite natural and simple. For some types of queries,

the processing can be naturally split in a well-deﬁned

sequence of stages. That is true for example for path,

or traversal queries, like the following:

A. Bounded traversal

MATCH (a)-[:RELASIONSHIP*1..n]-(b)

WHERE a.name = ’Value’ AND ...

RETURN b

B. Unbounded traversal

MATCH (a)-[:RELASIONSHIP*]-(b)

WHERE a.name = ’Value’ AND ...

RETURN b

In both cases during the query execution the paths

starting with nodes with particular names values and

progressing alongside speciﬁed relationships are tra-

versed. The execution may perform additionally

checks of some properties of encountered nodes if re-

quired by conditions following AND in the above que-

ries.

When executing such queries over encrypted

graph database in the original CryptGraphDB, the en-

cryption layer adjustment may be required for the pro-

perties of all nodes which may be encountered during

traversal, if conditions checks are present in the query.

As before query execution it is not generally possible

to identify nodes that will be traversed, the encryption

adjustment will be done everywhere (all nodes) where

the properties required for checks are present.

We propose, instead of such oblivious and static

adjustment to perform dynamic traversal-aware adjus-

tment, following the simple principles:

• Encryption adjustments and traversal query exe-

cution are interlaced;

• The adjustments happen in between of traversal

steps;

• The adjustment is performed to enable one step

of traversal using all information accumulated to

this step, in particular the set of nodes traversed so

far.

Intuitively, it is plausible that following these prin-

ciples we have a chance to do more focused adjust-

ment, not everywhere, but just along the query execu-

tion path. We conﬁrm this intuition in the following

subsection by considering a case study.

4.1 Case Study

For the case study we consider a particular graph da-

tabase instance presented in Figure 1. In this example

scenario we have nodes with the label Person, and

two properties of interest: name and age. Consider

the following Cypher query:

MATCH (x: person)-[:Knows]->(y)

WHERE x.name = "Tom" AND y.age = "22"

RETURN y

We consider the execution of this query in three

modes: 1) non-encrypted; 2) encrypted using origi-

nal CryptGraphDB adjustment; 3) encrypted using

traversal-aware adjustment.

Traversal-aware Encryption Adjustment for Graph Databases

383

Name:

Smith

age: 22

Name:

Tom

age: 39

Name:

Tom

age: 29

Name:

Smith

age: 35

Name:

Perry

age: 38

Name:

Tom

age: 40

Name:

Lee

age: 18

Name:

Perry

age: 38

Name:

Sara

age: 20

Name:

Jones

age: 32

Knows

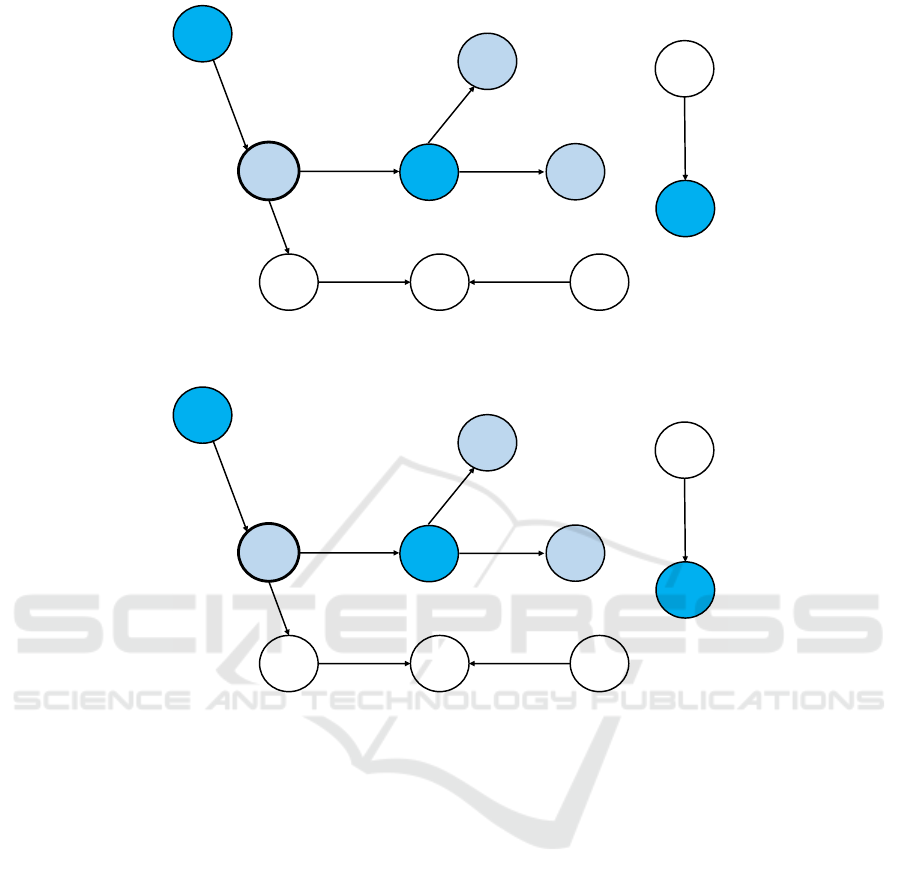
Figure 1: Data layout at the server of the graph database.

4.1.1 Non-encrypted Mode

WHERE clause consists of two conditions: initially,

WHERE name = "Tom", when this part is exe-

cuted it leads to have three nodes to be traversed/

checked: {Smith,22},{Smith,35},{Lee,18}

(these are reachable from {Tom,29} node in one

step via Knows relation). Then check the second part

of the query which is the age = 22, based on the

previous result, this execution showed that the ﬁnal

result is: {Smith,22} node.

4.1.2 Original CryptGraphDB Adjustment

Initially, each property in the graph is dressed in

onion of encryption with RND as outermost layers.

At this point, the server can learn nothing about

the data content other than the number of nodes,

properties, and relationships. To execute the query

over encrypted store it is required to lower encryption

of name and age to level DET ( as we need equality

checks). In this case, an update query is required UP-

DATE Label SET P2 Onion1 = DECRYPT

RND, and then RETURN P1, P2, P3, etc.,

WHERE P1 = "D1" AND P2 = "G83", where

D1 and G83 are an encryption of Tom and 22,

respectively. The results are decrypted and return

them to the user.

More details on this follows. In step (1), proxy

sends to the DBMS: UPDATE Database, SET Pro-

perty1 = DECRYPT RND(Property). Because all

the database properties on RND layer, as illustrated

in Figure 2. DBMS decrypts entire name and

age properties to DET layer: Dec.P,Eq,RND

(X11) = D1, Dec.P,Eq,RND (G71) =

G68, Dec.P,Eq,RND (X77) = D6, and so

on. Proxy updates its internal state to log that entire

name and age properties are now at DET layer in

the DBMS, as can be seen in Figure 3. In step (2),

proxy encrypts Tom and 22, to their Equality onion,

DET layer encryption value of D1 and G83. Proxy

generates query and sends it to DBMS:

MATCH (x: person1)-[:Knows1]->(y)

WHERE x.name1 = "D1" AND y.age1 = "G83"

RETURN y

and in step (3), proxy sends decrypted result Smith

and 22 to the application.

We notice that with this encryption adjustment

procedure after the query execution the equality of

{name,age} for each node becomes apparent. This

information on equality is not related to the result of

the query and is not strictly necessary for computing

the result, as these nodes are not connected to node

Tom.

4.1.3 Traversal-aware Encryption Adjustment

Consider the example schema shown in Figure 1. Ini-

tially, each node and each property in the graph is

dressed in equality onion of encryption, with RND as

outermost layers, as shown in Figure 2. At this point,

the server can learn nothing about the data values. Re-

turn now to our running query example Q:

MATCH (x: person)-[:Knows]->(y)

WHERE x.name = "Tom" AND y.age = "22"

RETURN y

In order for this query to be executed one needs

ﬁrst to adjust the encryption of name to layer DET. To

do so, the query UPDATE Label SET P1 On-

ion1 = DECRYPT RND is issued, where P1 cor-

responds to name. Then we execute the query Q

performing the initial search for nodes when the path

required in the original query Q may start:

MATCH (x: person1)-[:Knows1]->(y)

WHERE x.name1 = "D1"

RETURN y AS result

Here result variable is used to store the result of

, property name1 corresponds to name, and D1 is

DATA 2018 - 7th International Conference on Data Science, Technology and Applications

384

Name1

: X77

Age1:

G22

Name1

: X66

Age1:

G77

Name1

: X11

Age1:

G71

Name1

: X33

Age1:

G36

Name1

: X55

Age1:

G36

Name1

: X99

Age1:

G40

Name1

: X88

Age1:

G90

Name1

: X47

Age1:

G72

Name1

: X14

Age1:

G73

Name1

: X56

Age1:

G39

Knows1

Figure 2: The nodes created at the DBMS server. The encryption is set at RND layer everywhere. Ciphertexts shown are not

full-length.

Name1

: D6

Age1:

G83

Name1

: D1

Age1:

G14

Name1

: D1

Age1:

G68

Name1

: D6

Age1:

G10

Name1

: D5

Age1:

G49

Name1

: D1

Age1:

G33

Name1

: D8

Age1:

G89

Name1

: D5

Age1:

G49

Name1

: D12

Age1:

G21

Name1

: D10

Age1:

G03

Knows1

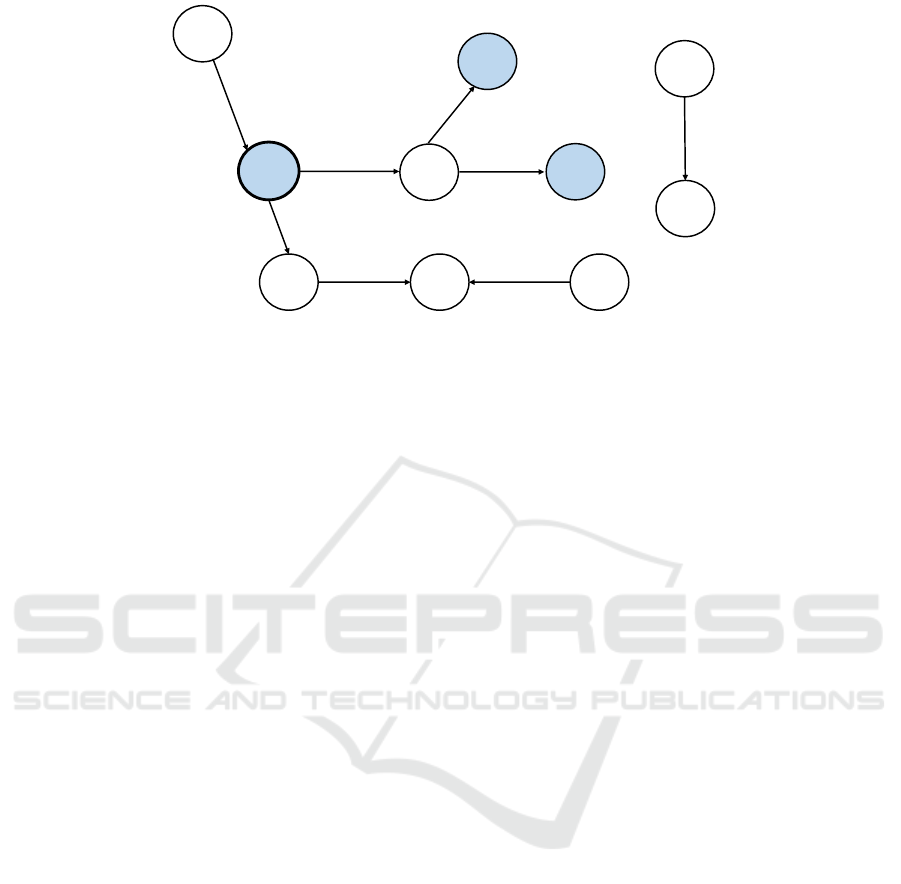
Figure 3: The encryption is adjusted to DET layer.

the encryption of Tom. The outcome shows that there

are only three nodes as the outgoing of Tom node.

Before processing the second part of the query Q, that

is WHERE y.age = "22", lowering encryption of

age property of nodes in result is needed to level

DET, as illustrated in Figure 4. Then we execute the

query Q

, implementing the next step of Q execution:

MATCH (x: person1)-[:Knows1]->(result)

WHERE result.age1 = "G83"

RETURN result

Finally, Proxy receives encrypted result D6 and

G83, decrypts them and sends decrypted result

Smith and 22 to the application.

Notice that unlike in the original encryption

adjustment procedure, the equality of age property

for both {Perry,38} nodes is not revealed here,

as it kept at RND layer at G36 and G72.

4.2 Discussion

The advantage of the proposed approach was that it

would not reveal the information that come from DET

layer more than necessary. To demonstrate this Figure

3 and Figure 4 show a signiﬁcant difference in the re-

sults when apply both the original CryptGraphDB en-

cryption adjustment strategy and the traversal-aware

encryption adjustment strategy. We notice when ori-

ginal strategy is applied it reveals more information

than necessary, such as the age of other nodes that are

not connected to Tom. By contrast, when traversal-

aware encryption strategy is applied, it reveals only

the information that required to execute the query. We

observe from Figure 4 that not all age property va-

lues are adjusted to DET layer, but only required va-

lues are adjusted, while the rest are still at RND layer.

Our technique shows a clear advantage by dynami-

cally adjusting encryption layers as query execution

progresses. In this way less information is revealed

to the potential adversary overseeing the execution of

the query on the encrypted store.

Traversal-aware Encryption Adjustment for Graph Databases

385

Name1

: D6

Age1:

G83

Name1

: D1

Age1:

G77

Name1

: D1

Age1:

G71

Name1

: D6

Age1:

G10

Name1

: D5

Age1:

G36

Name1

: D1

Age1:

G40

Name1

: D8

Age1:

G89

Name1

: D5

Age1:

G72

Name1

: D12

Age1:

G73

Name1

: D10

Age1:

G39

Knows1

Figure 4: Traversal-aware encryption adjustment. Ciphertexts shown are not full-length.

5 RELATED WORK

In this section, we compare related work with our ap-

proach. Some of the mechanisms used in traversal-

aware encryption adjustment are built on prior work

from the cryptographic collection.

CryptDB is an approach (Popa et al., 2011a) that

has completely explored access control for SQL que-

ries on encrypted relational data. The CryptDB archi-

tecture supposes a proxy between the users and the

server. The basic idea is that by selecting an appro-

priate encryption scheme, at the server side no need

to decrypt the data that stored on the database server

in an encrypted form, not even during the execution

of the queries. One of the CryptDB advantages is that

no need to change the server software. All process

is implemented by intercepting users queries, rewri-

tes them and passes to the server for execution. In

(Popa et al., 2011a; Popa et al., 2011b) The issue of

information leaks during encryption adjustment in re-

lational databases is discussed and special Join-aware

encryption scheme to reduce the leaks is proposed.

In more recent work (Sarfraz et al., 2015) the idea

of CryptDB has been further developed to include ﬁne

grained access control using advanced cryptographic

primitives. The proposed encryption adjustment pro-

cedure takes into account the data requirements of the

query as well as particular, users and groups of users

access rights.

In (Aburawi et al., 2018) the original CrypDB ap-

proach has been transferred to the context of graph

databases. The basic idea is the same as in relati-

onal CrypDB: the execution of the graph query is

achieved after translating the query into an encryp-

ted form, which later executed on a server without

decrypting any data. Each encrypted result then is

sent back to the user where they are ﬁnally decryp-

ted. The proposed design is implemented for Neo4j

graph DBMS and Cypher as a query language. It has

been conﬁrmed that SQL-aware encryption schemes

can be smoothly reused as Cypher-aware encryption

schemes, together with keeping the beneﬁt of the per-

formance of traversal graph queries over equivalent

relational ones. The mechanism presented in (Abu-

rawi et al., 2018) reported the efﬁciency of query im-

plementation for different types of queries on encryp-

ted and non-encrypted Neo4j graph databases. The

simple strategy of encryption adjustment prior to the

query execution has been proposed. While efﬁcient

in execution it may reveal more information about the

data than necessary. In this paper we show how to

reveal less information using dynamic encryption ad-

justment.

6 CONCLUSION

In this paper, we proposed traversal-aware encryp-

tion adjustment for graph databases, a novel solution

that supports executing cypher queries over encrypted

graph databases. We have shown that when querying

encrypted graph databases, dynamic traversal-aware

encryption adjustment provides with better security

protection of database content, as compared with the

static adjustment performed before query execution.

Our current and future work includes implementing

traversal-aware encryption adjustment for CryptGrap-

hDB, and empirical evaluation of related trade-off be-

tween security and query execution efﬁciency.

DATA 2018 - 7th International Conference on Data Science, Technology and Applications

386

REFERENCES

Aburawi, N., Lisitsa, A., and Coenen, F. (2018). Querying

encrypted graph databases. In 4th International Con-

ference on Information Systems Security and Privacy,

pages 447–451. Proceedings.

Cypher (2015). Introduction to cypher. https://neo4j.com/

developer/cypher-query-language/. Accessed on

2018-02-08.

Finley, K. (2011). Five graph databases to consider.

https://readwrite.com/2011/04/20/5-graph-databases-

to-consider/. Accessed on 2018-04-11.

neo4j (2015). Introducing the neo4j graph platform.

https://neo4j.com/. Accessed on 2018-01-13.

Popa, R. A., C.M.S. Redﬁeld, N. Z., and Balakrishnan, H.

(2011a). Cryptdb: Protecting conﬁdentiality with en-

crypted query processing. In 23rd ACM Symposium

on Operating Systems Principles, pages 85–100. Pro-

ceedings.

Popa, R. A., Zeldovich, N., and Balakrishnan, H. (2011b).

Cryptdb: A practical encrypted relational dbms. In

Computer Science and Artiﬁcial Intelligence Labora-

tory, Cambridge, MA. Technical Report MIT-CSAIL-

TR-2011-005.

Robinson, I., Webber, J., and Eifrem, E. (2013). Graph Da-

tabases. OReilly Media, Inc., United States of Ame-

rica, 1st edition.

Sarfraz, M. I., M. Nabeel, J. C., and Bertino, E. (2015).

Dbmask: Fine-grained access control on encrypted re-

lational databases. In 5th ACM Conference on Data

and Application Security and Privacy, pages 1–11.

Proceedings.

Traversal-aware Encryption Adjustment for Graph Databases

387