
A Set of Optimal Looks on a Symmetric Target
Bao Nguyen
Defence Research Development Canada, 101 Colonel By Drive, Ottawa, Canada
School of Mathematics and Statistics, University of Ottawa, 585 King Edward Avenue, Ottawa, Canada
Keywords: Search and Detection, Search and Rescue, Mine Hunting, Symmetry, Mirror Symmetry, Look Angles,
Multiple Looks, Optimization, Variational Calculus.
Abstract: In this paper, we identify a set of multiple looks from symmetry that optimize the expected probability of
detection in a mine hunting operation or in a search & rescue mission. We assume that the target exhibits
mirror symmetry, i.e., that the left hand side of a target is the mirror image of the right hand side of the same
target. In addition, it is assumed that the cross section is maximal at the interface between the left hand side
and the right hand side and decreases monotonically as we move away from the interface. The optimal
strategy consists of choosing aspect angles to inspect a target to ensure that the probability of detection is
maximal. This is generally an NP-hard problem in the sense that to find the optimal angles in
n
dimensions
normally consumes a lot of computational power. Fortunately, in this problem, we are use a novel
combination of variational calculus and symmetry principles to determine analytically the locally optimal
angles. The solutions will help the operators plan for an effective strategy in a mine hunting operation or in
a search and rescue mission. Such a strategy is robust as most targets of interest possess approximate mirror
symmetry along one or more axes. For example, a human body or a canoe or a mine when cut in half yield
approximately such symmetry.
1 INTRODUCTION
In this paper, we examine a problem where a
searcher can observe a target from multiple look
angles. This problem arises naturally in the context
of search and detection, or mine countermeasure
operations. We show that the angular dependence
affects the overall probability of detection
significantly even though this dependence is often
overlooked in the open literature.
Indeed, the formula for the probability of
detecting a target in a random search is widely used,
yet it assumes no angular dependence (Koopman
1999). The importance of the look angle in
perception of a target is not just intuitively evident,
but has also been demonstrated both theoretically
and experimentally. The ideas could be found for
example in (Wettergren and Baylog 2010) & (Zerr,
Bovio and Stage 2000) and many more such as (Ji
and Liao 2005) or (Runkle et al. 1999). As the paper
unfolds, it will be seen that our approach is different
from the current literature in that we identify a set of
all optimal angles.
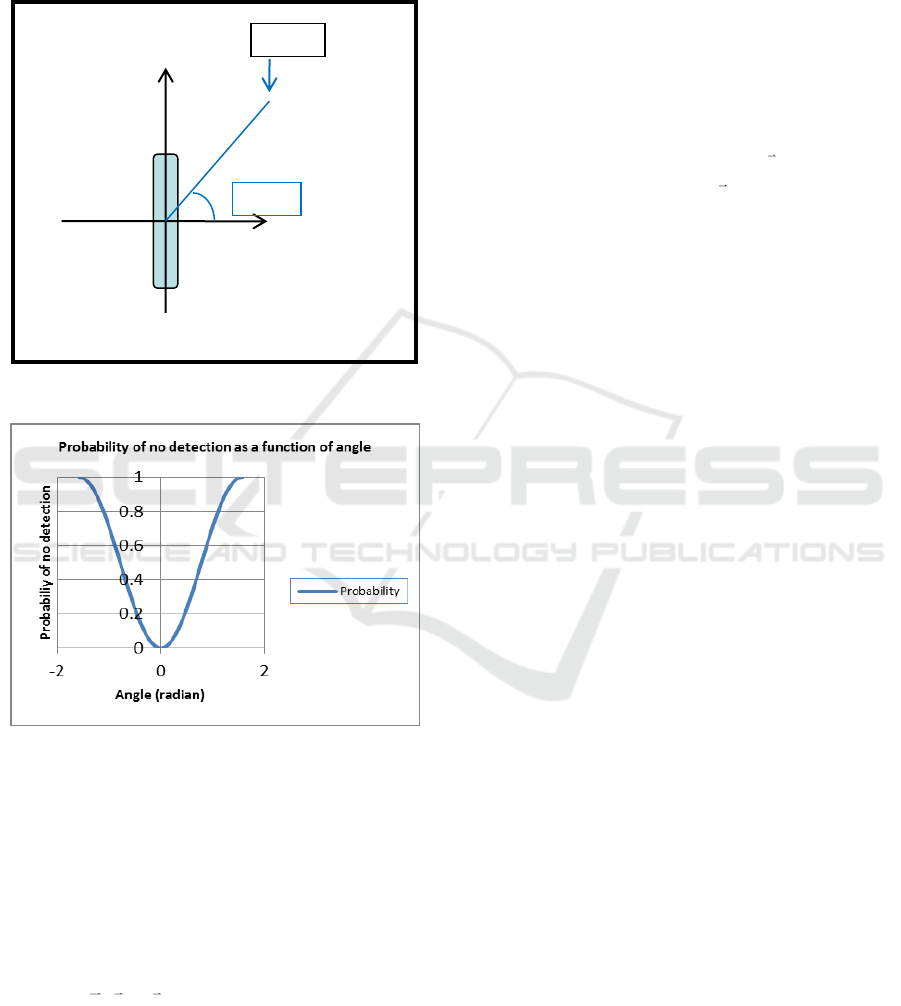
For completeness, we define the look angle as
shown in Figure 1. Each look angle is associated
with a look. For brevity, we call the look angle
simply the angle. It is measured counter clockwise
from the positive horizontal axis. The zero degree
(zero radian) angle corresponds to the look on the
long side of the target while the ninety degree (
/2
radian) angle corresponds to the look on the short
side of the target. The look angle is periodic with
period equal to 180 degrees (
radians).
For a general class of single look angular
probability of no detection, as shown in Figure 2, we
provide a strategy to determine the locally optimal
probability of detection based on
n
observations at
various angles, or simply
n
looks. That is, if an
observation is made once at an angle
x
then the
corresponding probability of no detection
gx
is
the corresponding value shown in Figure 2. For
illustration purposes, we assume that
2
sing x x
.
Note that
gx
is symmetric around zero degrees
(zero radians).
There are many real life targets than can be
approximated with this type of symmetry including
canoes, ships, submarines, mines and human bodies.
In this paper we call it the mirror symmetry; that is,
the left hand side of a target is the mirror image of
Nguyen, B.
A Set of Optimal Looks on a Symmetric Target.
DOI: 10.5220/0006921104770485
In Proceedings of 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2018), pages 477-485
ISBN: 978-989-758-323-0
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
477
the right hand side of that target. The difficulty of
detecting such targets depends for example on the
cross sections of the targets that are visible to the
sensor. The probability of (no) detection is assumed
to be proportional to the cross section of a
cylindrical target.
Figure 1: Look angle
x
.
Figure 2: Probability of no detection as a function of
angle.
This problem is intractable using calculus since
each look is independent of one another yielding a
multi-dimensional problem. The explicit expression
for the overall probability of detection is hopelessly
complicated even when the single probability of
detection is simple and the number of looks is small.
(Press et al. 1999): “Don’t be fooled by the
apparent notational similarity of (multi
dimension
0F
) and (one dimension
0F
)
(where are the roots to be determined). Simultaneous
solution of equations in dimensions is much more
difficult than finding roots in the one-dimensional
case. The principal difference between one and
many dimensions is that, in one dimension, it is
possible to bracket or “trap” a root between
bracketing values, and then hunt it down like a
rabbit. In multidimensions, you can never be sure
that the root is there at all until you have found it.”
Furthermore, even if we can bracket the roots
then the techniques available in (Press et al. 1999)
only provide numerical solutions which vary from
one model of angular probability to another and
hence require extensive computations prior to a
search.
(Torns and Zilinska 2007): “In general, the
problem of finding the exact values
x
that minimize
a given objective function
fx
is computationally
difficult (NP-hard); …Crudely speaking, NP
hardness means that it is not possible to have an
algorithm that solves all optimization problems in a
reasonable time.”
The problem that we consider has all the features
and difficulties that are described above. We resolve
these difficulties by making use of the symmetry of
the single angular probability of detection function.
This novel symmetry argument yields a number of
simple and easy to use formulae for the optimal
angles. In addition, these formulae hold true for the
general class of single probability of detection
curves shown in Figure 2. That is, the probability of
no detection is an even and decreasing function of
angle based on the definition of angle shown in
Figure 1.
gx
can be convex, can be concave, and
can be neither convex nor concave.
Note that (Waterhouse, 1983): “That is, as soon
as the symmetry of a problem is brought out, people
are inclined to say that *by symmetry* the extreme
value must occur when the variables are equal. But a
bit of thought shows that there is no simple
symmetry argument to this effect. Indeed, there
cannot be, because such a symmetry conclusion is
sometimes false (Bouniakovsky 1854)”. To avoid
this pitfall, we will find all locally optimal roots.
2 SEARCH EXPERIMENT
In this Section, we provide a simple demonstration
to qualitatively illustrate the dependence of the
probability of detection as a function of angle. This
experiment was also reported in (Nguyen and
Mirshak, 2016). We put a pen on a Christmas tree
and we take pictures of the tree (including the pen)
as we rotate the observation angle by approximately
30
degrees each time by rotating the tree.
Angle
Look
DMSS 2018 - Defence and Military
478

Figure 3: Pen observed at -90 degrees.
This pen has approximately mirror symmetry and
is approximately six inches in length. The tree is
about one meter in height. The distance between the
camera and the tree is approximately
1.5
meters. A
cat is shown to give an idea of the scale. We used a
Canon Power Shot A530 digital camera to take the
pictures. It is difficult to identify the pen, from
Figure 4 and Figure 8, when the angle is
60
degrees. It is nearly impossible, from Figure 3 and
Figure 9, when the angle is
90
degrees. However,
it is easily identified when the angle is zero degrees
(zero radians) or
30
degree. Zero degrees (zero
radians) correspond to the look perpendicular to the
long side of the pen.
Figure 4: Pen observed at -60 degrees.
Figure 5: Pen observed at -30 degrees.
Figure 6: Pen observed at zero degrees.
Figure 7: Pen observed at 30 degrees.
A Set of Optimal Looks on a Symmetric Target
479

Figure 8: Pen observed at 60 degrees.
Figure 9: Pen observed at 90 degrees.
3 MODELLING THE LOOK
ANGLE
As shown in Section 2, the probability of detection
of a target depends on the look angle in search and
rescue operations. The effectiveness of such an
operation depends on the performance of the sensor.
There are two types: the probability of detection as a
function of range and the probability of detection as
a function of look angle. The probability of detection
as a function of range is nearly a constant; hence we
focus only on the angular dependence. For more
details on the range dependence, we refer the reader
to (Nguyen et al. 2008).
The probability of detection as a function of
range is primarily a characteristic of the sensor,
while the probability of detection as a function of
angle is primarily a characteristic of the target. All
ranges and angles are measured on the two
dimensional plane formed by the sensor beam and
the direction of motion of the searcher carrying the
sensor. Most targets of interest have approximate
mirror symmetry; that is the left hand side of a target
is the mirror image of the right hand side of the same
target. Human bodies, canoes, ships and mines
belong to this type of symmetry. Therefore, to build
a robust search strategy, we assume that the target
has (approximately) the mirror symmetry. The look
angle is defined as the counter clockwise angle
between the sensor beam and the short axis of
symmetry of a cylindrical (positive horizontal axis)
target as shown in Figure 1. A look angle of zero
degrees corresponds to the observation of the long
side of the target. A look angle of ninety degrees
corresponds to the observation of the short side of
the target.
The corresponding angular probability of no
detection curve
gx
in Figure 2 shows that the
detectability of a target reaches a maximum when its
look angle is perpendicular to the sensor beam and
this angular probability decreases symmetrically
with respect to that perpendicular case where we use
2
sing x x
for illustration purposes. Such an
expression for
gx
is similar to a specific case of
target angular dependence, (Gilani et al. 2015). In
addition,
2
1 1 sing x x
is approximately
equal to the normalized cross section of a cylindrical
target. It is very clear from Figure 2 that the
probability of detection is substantially degraded if
the look angle differs from zero degrees (zero
radians).
The following assumptions are imposed on the
function
gx
:
1.
gx
is periodic with period equal to
;
2.
gx
is an even function i.e.
g x g x
;
3.
gx
is minimal at
0x
and
4.
gx
is increasing between zero and
/2
.
4 LOCAL OPTIMAL
CONDITIONS
In this Section, we determine the set of all angles
that optimize the probability of detection. We
assume that a target is observed
n
times possibly at
n
distinct angles. The proof of Lemma 4A is
DMSS 2018 - Defence and Military
480

described in (Nguyen and Bourque, 2012a & 2012b)
which make use of variational calculus (Gelfand and
Fomin 1963). A different approach was made in
(Bourque and Nguyen, 2011) based on inequalities
of a quadratic equation.
Let
i
be the look angle of the ith
observation
0,..., 1in
. We note that the
probability of detection (at least one detection),
P
can be written as:
1PG
(1)
where
G
is the probability of no detection
defined as:
/2
01
/2
...
n
dx
G g x g x
(2)
Eqn (2) assumes that the orientation of the target
is randomly uniform. That is, the probability density
function is equal to
1/
. The set of
n
looks
yields no detection when each look yields no
detection. Therefore, the probability of no detection
based on
n
looks is the product of the probability of
no detection of each look:
01
...
n
g x g x
.
When this product is integrated over all angles
x
and weighted by the density distribution
1/
, we
obtain the expected probability of no detection based
on
n
looks:
G
.
Lemma 4A.
G
is locally optimal, i.e.,
0G
if and only if
ii
f x f x
for
1,..., 1in
where
/2
0 1 1
/2
/2
00
0
/2
1 2 1
1
/2
11
/2
11
0
/2
1
1
/2
21
' ...
'
'
...
'
...
... '
n
n
n
n
nn
dx
G g x g x g x
dx
g x f x f x
g x g x g x
dx
G
gx
dx
g x f x f x
gx
dx
G
g x g x
dx
/2
11
0
'
nn
g x f x f x
(3)
and
1
0
1
n
i j i
j
f x g x
gx
(4)
For example,
0 1 1
11
11
0
...
...
...
n
n
n
f x g x g x
g x g x
g x g x
fx
(5)
Lemma 4A implies that
11
11
...
...
n
n
g x g x
g x g x
(6)
Lemma 4B. The above holds when
11
,..,
n
11
,..., mod
n
for
, 1,..., 1i j n
.
Proof of Lemma 4B. We can show this by induction.
We have shown above that it is true for
11n
.
Assume the contrary, i.e. there is no pair
mod
ij
and
00g
, we can choose
1
x
so that the LHS of Eqn (6) is zero while the
RHS is not zero. This is impossible. Hence, we can
infer that
11
mod
without loss of generality.
Therefore,
21
21
...
...
n
n
g x g x
g x g x
(7)
The above implies that by induction:
2 1 2 1
,..., ,..., mod
nn
(8)
Therefore,
1 1 1 1
,..., ,..., mod
nn
(9)
Lemma 4C. Assume that
mod
i
i
for
0,..., 1in
then
/kn
for
0,...,kn
or
' / 1kn
for
' 0,..., 1kn
.
Beside the roots in Lemma 4C, there are other roots
satisfying Eqn (8) as shown below.
First, we can set any root
0,..., 1
i
in
to be
zero. Second, the critical point must obey the
following symmetry
2 2 mod 2
. The two
criteria signify that there are two types of critical
points as shown below.
A Set of Optimal Looks on a Symmetric Target
481

Theorem 4A. Using the two criteria, we obtain
two types of critical points.
Type 1 critical points consist of roots that appear
together from
0, / ,..., 1 /m m m
possibly
more than once as well
as
0, / 2 ,..., 2 1 / 2m m m
also possibly
more than once where
1 ,2m m n
.
Type 2 critical points consist of roots that differ
by
/mn
where
1,..., 1mn
. That is,
0, ,..., 1n
.
Proof. We can infer from the second symmetry,
the periodicity and the monotonicity of
gx
that
is composed of multiple sub cycles consisting
of
0, / ,..., 1 /m m m
for
1 mn
.
It is simple to show that the two types of critical
points satisfy the two criteria above. To show
completeness of the two types, we make use of
contradiction. Specifically, we assume that
is
comprised of either type in addition to at least
another sub cycle
0, / ',..., ' 1 / 'm m m
where
1'mn
such
that
/ ' / , / 2 modm m m
and
/ ' modm
and show that
does not
satisfy the two criteria. We will rotate all the roots
of
such that
/ ' / ' / ' 0m m m
.
For type 1 critical points,
2 0, / ,..., 1 /
2 0 / ', / / ',..., 1 / / '
2 0 / ', / / ',..., 1 / / '
mod
a
a
a
m m m
m m m m m m
m m m m m m
and
2 0, / 2 , ..., 2 1 / 2
2 0 / ', / 2 / ',..., 2 1 / 2 / '
2 0 / ', / 2 / ',..., 2 1 / 2 / '
mod
b
b
b
m m m
m m m m m m
m m m m m m
where
a
and
b
are the redundancies of the
corresponding roots. It is shown above that the
transformed roots no longer satisfy the second
criteria. That is,
2 2 mod 2
. The proof is
similar for type 2 critical points.
Example 4B. For clarity, we provide below all
the critical points for six looks
6n
:
a.
0,0,0,0,0,0
;
b.
0,0,0,0,0, / 2
;
c.
0,0,0,0, / 2, / 2
;
d.
0,0,0, / 2, / 2, / 2
;
e.
0, / 2
and
0, / 4, / 2,3 / 4
;
f.
2
0, / 3,2 / 3
where the superscript
2
means that the set
0, / 3,2 / 3
is
repeated twice and
g.
0, / 6,2 / 6,3 / 6,4 / 6,5 / 6
.
Technically there are also other critical points
such as
0,0, / 2, / 2, / 2, / 2
. However, by the
periodicity of
gx
we can shift these roots by
/2
without changing the probability of detection i.e.
/ 2, / 2,0,0,0,0
yields the same probability of
detection as the one from
0,0, / 2, / 2, / 2, / 2
.
Furthermore, the evenness of
gx
allows us to infer
that
/ 2, / 2,0,0,0,0
yield the same probability of
detection as the one from
0,0, / 2, / 2, / 2, / 2
.
5 GLOBALLY OPTIMAL ROOTS
It turns out that the critical point consisting of
0, / ,..., 1 /n n n
yields the globally
maximum probability of detection. We name this
critical point the equidistant roots.
Theorem 5A. If
gx
is logarithmically concave
then the equidistant roots yield the globally
maximum detection probability.
Proof of Theorem 5A. In both types of critical
points, the root that is equal to zero occurs at least
twice except for the equidistant roots. We choose
0
and infinitesimal then modify the two zero
roots one by
and the other by
. This will
generate a higher detection probability than the one
with two zero roots. To show this, we
define
' , ,*
where the
*
represents all the
remaining roots of a critical point
. We now
determine the expected probability of detection of
'
:
/2
/2
' **
dx
G g x g x
(10)
where
**
represents the product of
gs
with the
remaining roots of the critical point
. Since
is
DMSS 2018 - Defence and Military
482

infinitesimal, the first order expansion in
can be
written as:
2
2
/2
2
/2
3
' **
' ''
gx
dx
G
g x g x g x
O
(11)
Logarithmic concavity means that
2
' '' 0g x g x g x
. In the non-trivial case
where
2
' '' 0g x g x g x
, this implies that:
'GG
(12)
Therefore, a critical point
with at least two
zero roots cannot yield the globally maximum
probability of detection. This eliminates all the
critical points except for the equidistant roots.
Hence, the equidistant roots must be the globally
maximum probability of detection.
We observe that there are many functions for a
symmetric target that are logarithmically concave
such as:
a.
2
sing x x
where
0
;
b.
2
/2
x
gx
where
0
;
c. the normal density distribution and
d. the exponential density distribution.
For the practical purpose of planning a search &
detection operation, the types of
gx
listed above
are representative of most targets of interest. This is
sufficient to guarantee the global optimality of the
equidistant roots.
We provide here examples when assuming
2
sing x x
. For convenience, we break the two
types of critical points into the following four
categories. For
0,..., 1in
:
1.
0
a
and
/2
b
where
a b n
;
2.
0, / ,..., 1 /
a
m m m
and
0, / 2 ,..., 2 1 / 2
b
m m m
such as
0, / 2
a
and
0, / 4,2 / 4,3 / 4
b
where
mn
and
2a m b m n
;
3.
0, / ,..., 1 /
p
m m m
where
m p n
and
4.
0, / ,..., 1 /n n n
.
The results below make use of the following identity
(Gradshteyn and Ryzhik 1980):
1
sin sin ...
1
sin 1 sin
2
v
xx
v
x v v x
v
(13)
where
v
is a positive integer. Using simple calculus,
we get
G
as follows:
1.
1/ 1/ 2, 1/ 2B a b
;
2.
2
1/ 4 1/ 2, 1/ 2
ab
B a b b
for the
case
0, / 2
a
and
0, / 4,2 / 4,3 / 4
b
;
3.
1
1/ 2 4
n
and
4.
1/ 4 1/ 2,1/ 2
np
Bp
.
where
,B x y
is the
B
function (Zwillinger, 1996).
We observe that all of the four results above can be
rewritten using factorial of integers. However, for
concision we express the results using the
B
function.
For illustration, we assume
6n
. Table 1
displays the set of all optimal roots for four looks
and the corresponding probabilities of no detection.
Clearly, we see that
0,0,0,0,0,0 231/1024 0.2256G
is the largest
among the five optimal roots. While
0, / 6, / 3, / 2,2 / 3,5 / 6 1/ 2048 0.0004883G
is the smallest implying that it provides the greatest
probability of detection.
It is also worth observing that the probability of
detection for one look is equal to
0
1 1/ 2 4 1/ 2
while the one for two looks with roots
0, / 2
is
equal to
1 1/ 2 4 7 / 8
. Therefore, the probability
of detection almost doubles when we go from one
look to two (optimal) looks. Figure 10 shows two
search patterns: one yielding one look and the other
two looks.
Table 1: Exhaustive set of optimal roots and their
corresponding probabilities of no detection.
G
0,0,0,0,0,0
231/ 1024
0,0,0, 0, 0, / 2
21/ 1024
0,0,0, 0, / 2, / 2
7 /1024
0,0,0, / 2, / 2, / 2
5 /1024
0, / 2 0, / 4, / 2,3 / 4
1/ 1024
2
0, / 3, 2 / 3
3 / 2048
0, / 6, / 3, / 2, 2 / 3,5 / 6
1/ 2048
A Set of Optimal Looks on a Symmetric Target
483

Figure 10: One (lhs) and two (rhs) optimal look search
patterns.
For comparison, we also compute the probability of
no detection for two points that are not locally
optimal. Namely
0, / 2, / 4, / 8, /16, / 32 0.02384G
and
0,0, / 2, / 2, / 4, / 4 0.01074G
. Clearly
they lie between
0,0,0,0,0,0 0.2256G
and
0, / 6, / 3, / 2,2 / 3,5 / 6 0.0004883G
.
6 DISCUSSION
In this paper, we show the significance of the look
angle dependency. The probability of detection can
improve substantially when we increase the number
of looks in addition to choosing the optimal looks.
As observed in Section 5, the probability of
detection almost doubles when we go from one look
to two optimal looks.
We have derived the optimality condition using
variational calculus that allows determining the
optimal roots in a general way. That is, the single
look no detection probability obeys a broad class of
functions that requires only symmetry and
monotonicity that is similar to
2
sing x x
. In
addition, the results apply to general
n
dimension
which is normally NP hard even when we seek for
numerical solutions.
In the near future, we will provide a stronger
proof showing the global optimality of the
equidistant angles and the effect of repeated looks.
Future work might also include the development
of general search patterns that would make use of
the optimal angles. There is already some evidence
in the open literature such as (Bays et al. 2011) and
(Nguyen et al. 2008) which assumes angular
dependencies and which we will build upon to
develop new concepts of search and rescue
operations.
ACKNOWLEDGEMENTS
The content of this paper comes mainly from a
Defence R&D Canada report (Nguyen et al. 2016).
The original contribution of this paper is essentially
Theorem 4A and Theorem 5A.
REFERENCES
Bays M., Shende A., Stilwell D. and Redfield S., 2011. ‘A
solution to the multiple aspect coverage problem’,
2011 IEEE International Conference Proceedings on
Robotics and Automation, Shanghai, pp. 1531-1537.
Bouniakovsky, V., 1854. ‘Note sur les maxima et les
minima d’une function symétrique entière de plusieurs
variables’, Bull. Classe Phys.-Math. Acad. Imper. Sci.
St. Petersburg, 12, pp. 353-361.
Bourque, A. and Nguyen, B.U., 2011. ‘Optimal sensor
configurations for rectangular target detection’, 9th
IEEE international conference on control and
automation, Santiago, Chile, pp. 455-460.
Gelfand, I. M. and Fomin, S.V., 1963, Calculus of
variations, Prentice-Hall, Inc., pp. 42-50.
Gilani, S.U., Shende, A., Nguyen, B.U. and Stilwell, D.J.,
2015. ‘Optimal relative view angles for an object
viewed multiple times’, Society of Photographic
Instrumentation Engineers (SPIE) Proceedings, Vol
9454.
Gradshteyn I.S. and Ryzhik, I.M., 1980. Table of
integrals, series, and products, Academic press, p. 33.
Ji, S. and Liao, X., 2005. ‘Adaptive Multiaspect Target
Classification and Detection with Hidden Markov
Models’, IEEE Sensors Journal, Vol 5, No 5, pp.
1035-1042.
Koopman B.O., 1999. Search and Screening: General
Principles with Historical Applications, The Military
Operations Research Society Inc., pp. 71-74.
Nguyen, B.U., Hopkin, D., and Yip, H., 2008.
‘Autonomous Underwater Vehicles – A
Transformation of Mine Counter Measure Operations’,
Defense & Security Analysis, Vol 24 No 3, pp. 247-
266.
Nguyen, B.U. and Bourque, A., 2012a. ‘An optimal tactic
for intelligent agents to conduct search & detection
operations based on multiple look angles’, Advances
in Knowledge-Based and Intelligent Information &
Engineering Systems, San Sebastian, Spain, pp. 139-
148.
Nguyen, B.U. and Bourque, A., 2012b. ‘A Robust and
Optimal Search Tactic using Multiple Looks’, 10th
World Congress on Intelligent Control and
Automation, Beijing, China.
Nguyen, B.U. and Mirshak, R., 2016. ‘Modeling the
expected detection probability for mine
countermeasure operations based on cross-section and
multiple looks’, The Journal of Defence Modeling and
DMSS 2018 - Defence and Military
484

Simulation: Applications, Methodology, Technology,
Vol 13, No 4, pp. 431-447.
Nguyen, B.U., Bourque, A., Hill, A., 2016. ‘A Robust
Optimal Search Tactic for Targets with Mirror
Symmetry’, Defence R&D Canada Technical
Memorandum, 2013-250.
Press, W.H., Teukolsky, S. A., Vetterling, W.T. and
Flannery, B.P., 1999. Numerical Recipes in Fortran
77, Cambridge University Press, pp. 340-343.
Runkle, P., Bharadwaj, P. K., Couchman, L. and Carin, L.,
1999. ‘Hidden Markov Models for Multiaspect Target
Classification’, IEEE Transactions on Signal
Processing, Vol 47, No 7, pp. 2035-2040.
Törns, A. and Žilinska, J., 2007. Models and Algorithms
for Global Optimization, Springer Science + Business
Media, p. 22.
Waterhouse, W.C., 1983. ‘Do Symmetric Problems Have
Symmetric Solutions?’, The American Mathematical
Monthly, Vol 90, No 6, pp. 378-387.
Wettergren, T.A. and Baylog, J.G., 2010. ‘Modeling
Sequential Searches with Ancillary Target
Dependencies’, Advances in Decision Sciences, Vol
2010, Article ID 472809.
Zerr B., Bovio, E. and Stage, B., 2000. ‘Automatic Mine
Classification Approach Based on AUV
Manoeuvrability and COTS Side Scan Sonar’,
Autonomous Underwater Vehicle and Ocean
Modelling Networks: GOAT2 2000 Conference
Proceedings, pp. 315-322.
Zwillinger, D., 1996. Standard mathematical tables and
formulae, 30th edition, CRC Press, p. 498.
A Set of Optimal Looks on a Symmetric Target
485
