Simple and Effective: An Adaptive Instructional Design for

Mathematics Implemented in a Standard Learning Management

System

Matthias Holthaus, Franziska Hirt and Per Bergamin

UNESCO chair on personalised and adaptive Distance Education, Swiss Distance University of Applied Science (FFHS),

Überlandstr. 12, Brig, Switzerland

Keywords: Technology-based Learning, Adaptive Learning, Cognitive Load, Expertise Reversal Effect, Learning

Management System, Log Files.

Abstract: This article shows how an adaptive instructional design in a standard learning management system was

realized within the framework of a straightforward technological concept with four components and with the

help of simple technological tools for a mathematics module. For this purpose, we have implemented a

didactic design with domain-specific online exercises in which the frequency of step-by-step support is

automatically adapted to the level of knowledge of the individual students. The consequence of this is that

students with lower pre-knowledge and/or a lower learning achievement receive more and other teaching

assistance than those with a high pre-knowledge or high performance. In our approach we assume that this

indirectly reduces the subjective task difficulties (intrinsic cognitive load) for beginners but also means

unnecessary repeating for advanced learners. The design of this teaching method is based on an adaptive

feedback mechanism with integrated recommendations. After a presentation of the didactic design and its

theoretical and empirical foundations, we report on the first results with a focus on the learning progress of

the various student groups. It has been shown that both weaker and stronger students benefit from the adaptive

tasks. Online activity is hereby a crucial factor.

1 INTRODUCTION

As a result of the life-long learning required in the

modern world, new forms of learning such as distance

learning as well technology-based learning are

gaining in significance (Bergamin et al., 2012). These

concepts and their flexible approaches enable many

people to pursue continued academic education in

situations in which traditional studies would be

difficult to accomplish (e.g. employment or

parenthood). From a didactic perspective, flexibility

also means taking the individual requirements of the

learner into account and incorporating respective

measures into the instructional design.

According to the Cognitive Load Theory and in

particular to the Expertise Reversal Effect (Sweller et

al., 2003), it is important to adapt the learning process

to the learner’s level of knowledge. Such

individualisation of learning possibilities can be

achieved through adaptive learning environments and

provide students with the chance to better handle the

challenges of life-long learning (Boticario and

Santos, 2006). In academia for instance, the design of

adaptive learning concepts is aimed at delivering an

optimal support for learners in consideration of their

differing levels of knowledge. Despite different levels

of pre-knowledge, learners should be able to finally

develop the same competences. At universities, this

usually happens less as a result of the learners

processing different learning content and more

through instructional support or content sequencing

adapted to the individual learners.

Today, there is an increasing number of

technological possibilities for implementing adaptive

learning. Numerous experimental investigations have

been carried out to test even the most complex

adaptive learning systems. Despite this, practical

implementations of adaptive technology-based

learning systems in real-life learning settings seem to

still be very rare (Somyürek, 2015). FitzGerald et al.

(FitzGerald et al., 2017) state that individualisation in

technology-based learning can be seen as positive and

promising but its implementation is difficult to

116

Holthaus, M., Hirt, F. and Bergamin, P.

Simple and Effective: An Adaptive Instructional Design for Mathematics Implemented in a Standard Learning Management System.

DOI: 10.5220/0006927601160126

In Proceedings of the 2nd International Conference on Computer-Human Interaction Research and Applications (CHIRA 2018), pages 116-126

ISBN: 978-989-758-328-5

realize. The application of experimental research into

prototypes and the following implementation in

everyday scenarios seems to be hard to achieve

(Scanlon et al., 2013). Murray and Pérez (Murray and

Pérez, 2015) predict that there is still a long way to go

before appropriate, sophisticated and intelligent

learning systems can be applied in practice. Bridging

the gap between research and practice requires results

of applied research and specific experience in the

implementation and application of relevant

technology-based learning systems, well-founded

instructional designs and large-scale investigations in

university contexts. However such research findings

are very scarce (Johnson et al., 2016).

This work seeks to bridge the gap between

experimental research and its practial application. In

this regard, we address the question of whether there

are currently any possibilities for implementing an

exemplary adaptive learning system in a classic

learning environment (Moodle), based on a cognitive

learning approach and on a fairly simple rule-based

instructional design but without the use of high-end

technology or machine learning algorithms. Drawing

on our experience in designing and implementing

course modules for online distance learning, we

demonstrate in this paper how an offer of adaptive

learning can be implemented in practice at university

level within a traditional Learning Management

System (Moodle). We further explore to what extent

instruction design based on the adaptation of task

difficulty, online activity and previous knowledge are

related and contribute to the improvement of learning

progress. Finally, we discuss the possibilities and

limitations of rule-based adaptive learning systems in

a standard Learning Management System (LMS) in

addition to the advantages for students.

2 THEORETICAL

BACKGROUND AND DESIGN

2.1 Instructional Implications of the

Cognitive Load

Optimal teaching of complex learning content needs

to deliberately take account of learners’ cognitive

load or actively manage it through instructional

interventions (Somyürek, 2015). The Cognitive Load

Theory (Sweller, 1988) can be used as a basis for this.

The Cognitive Load Theory strongly focuses on the

interplay between two interacting components of the

cognitive system: The working memory and the long-

term memory. According to the Cognitive Load

Theory, the long-term memory is where all our

knowledge is stored and has an unlimited capacity.

The working memory, by contrast, is used to

consciously process new information but is

significantly limited in terms of its capacity and

durability (Kalyuga, 2011a). Nowadays, we

differentiate between two kinds of cognitive load

during learning: the intrinsic load and the extraneous

load. The intrinsic load is occupied by cognitive

processes which are necessary to process learning

material and can be affected by the subjective

complexity or difficulty of the learning content. The

extraneous load is consumed by cognitive processes

that are not vital for learning, caused by unfavourable

design or presentation of the learning material

(Kalyuga, 2011a, b). The extraneous and intrinsic

load combined cannot exceed the limited capacity of

the working memory (Paas et al., 2003). So, if the

extraneous load is filled with unnecessary

unfavourable design or presentation of the learning

material less intrinsic load can be allocated to

processing learning material. If learning activities

require too much cognitive capacity (overload),

learning is hindered. In addition to the objective

difficulty of the learning content and instructional

design, the extent of the current cognitive load on the

working memory is also determined by

characteristics of the learner. As already mentioned,

working memory and long-term memory interact

with one another. The extensive schemata stored in

the long-term memory enable complex learning

content to be processed more easily in the working

memory because elements can already be collated in

higher-order units thanks to the available schemata.

This reduces the intrinsic load and enables certain

processes to take place routinely. In this way, there is

more cognitive capacity left for new content

(Kalyuga, 2011a). Consequently, the level of

available expertise/knowledge in the long-term

memory exerts considerable impact on cognitive load

in the working memory (Kalyuga, 2007b).

The influence of this effect on the instructional

design can be demonstrated via the so-called

Expertise Reversal Effect. This theory postulates that

the teaching support which is beneficial for novices

can be superfluous or even detrimental to experts and

vice versa (Kalyuga, 2007a, b). ‘Reversal’ here refers

to the fact that the relative effectiveness of didactical

aspects may reverse for differing levels of learners’

expertise (Lee and Kalyuga, 2014). One important

application of the Expertise Reversal Effect relates to

the degree of the learners’ instructional guidance. On

the one hand, if novices do not receive sufficient

external instructional guidance during complex

Simple and Effective: An Adaptive Instructional Design for Mathematics Implemented in a Standard Learning Management System

117

learning activities, this leads to poor problem-solving

strategies or arbitrary trial-and-error attempts. On the

other hand, superfluous instructional guidance for

experts, forcing the learners to squander their

resources to compare and connect what they already

know with their own schemata, may also lead to

inefficiency through high extraneous load (Kalyuga,

2011a). In this sense, the assumption is that direct

instructional guidance can balance out a lower level

of knowledge in the long-term memory of novices by

clearly indicating how they should proceed in a

certain situation while this should be avoided for

experts (Kalyuga, 2007b; Kalyuga and Sweller,

2005). For us, this means that learners are to be

provided with instructional guidance (e.g. step-by-

step instruction) at the start of the learning process

(novices) to enable them to handle tasks and optimise

the cognitive load. This guidance can then be

gradually reduced as they gain more expertise (see,

for example, fading scaffold; Merriënboer and

Sluijsmans, 2009). The fundamental educational

implications of the Cognitive Load Theory and, in

particular, the Expertise Reversal Effect have been

confirmed by numerous studies. In order to tie in

some contradictory research results with theory,

Kalyuga and Singh (Kalyuga and Singh, 2016) stress

that the validity of this theory is limited to the

acquisition of subject-specific knowledge as a

learning goal. For other educational goals (e.g.

promoting self-regulated learning skills or learning

motivation), the assumptions of Cognitive Load

Theory (e.g. suitability of much instructional

guidance for novices) are not necessarily applicable.

Learners, particularly novices, may feel

overburdened by the notion of undertaking the

adjustment of their learning (Kirschner and van

Merriënboer, 2013). Therefore technology-based

adaptive learning support may be an option to

enhance effectiveness of learning.

2.2 Adaptivity in Technology-based

Learning Environments

In contrast to the traditional technology-based

approaches adaptive concepts allow the learning

content, navigation and suitable learning support to

be presented in a dynamic environment continually

changing based on individual requirements. In

principle, adaptive learning support can be provided

at the macro level (e.g. at the level of the academic

goals of an individual) or at the micro level (e.g. at

the level of individual courses or tasks). In this study

we focus on this second level. There is a wide range

of possibilities how to adapt individual characteristics

on a course level (for an overview see e.g. Nakic et

al., 2015). Three main factors can be established as

basis of adaptation: (1) Stable or situation-related

personal characteristics such as gender, culture, style

of learning, knowledge or emotions, (2) content-

specific characteristics such as topics or task

difficulty and (3) context-based characteristics such

as learning time or place (Wauters et al., 2010). Three

main factors can be established as basis of adaptation:

(1) Stable or situation-related personal characteristics

such as gender, culture, style of learning, knowledge

or emotions, (2) content-specific characteristics such

as topics or task difficulty and (3) context-based

characteristics such as learning time or place

(Wauters et al., 2010). On the basis of these factors,

different dimensions of the learning experience can

be adapted. For instance, the level of task difficulty,

the level of detail of the explanations, the frequency

of hints, or the modus of presentation (video, text,

figure...) can be adapted to match the needs (basis of

adaptation) of individual students.

In our instructional design we focus on task

difficulty, actual knowledge and giving different

adaptive support. Depending on the learner's level of

knowledge, the system recommends tasks with more

or less detailed instructions and thus with different

degrees of difficulty. This way less performant

learners are given tasks with more support and

assistance. The support and assistance is reduced for

more efficient learner increasing the difficulty of the

tasks. Aiming to reduce the cognitive load.

Based on a model by Zimmermann et al.

(Zimmermann et al., 2005), we developed the

methods and components for processing and linking

learning data with adaptive instructional

interventions. We delivered interventions in the form

of hints and recommendations integrated in task

feedbacks displayed by our learning management

system Moodle. Conceptually, the system is based on

four components resulting in the adaptation

mechanisms. The components themselves use

learning data, which must be measured and stored

continuously. The first component are the sensors.

These use data from tasks worked on by learners,

specifically if a certain point has been achieved or

not. As an entry point we use the data from a previous

knowledge test, which evaluates the expertise with

which the learners start the course. Further tests and

assessments then form an additional data base for the

sensor component. The second component is the

analyser. This component collects, evaluates and

interprets the data measured by the sensors. The

analyser then transfers this information to the third

component, the controller. This component

CHIRA 2018 - 2nd International Conference on Computer-Human Interaction Research and Applications

118

determines whether a threshold is met. Depending on

the outcome the controller determines if and to what

extent the adjustment object (for example a task) is to

be changed by one or more educational interventions.

The last and fourth component is the presenter, which

finally triggers the customized display of the concrete

learning objects.

Based on the model with its four components, the

learners are classified as "low" or "high" performers,

depending on their learning performance. In addition,

the result of each individual learning step is registered

and compared with a threshold value. Consequently,

learners receive instructions and learning support

adapted to their learning performance and behaviour.

We chose a rule based operating, adaptive

learning system with a fixed set of rules for two

reasons: On the one hand our learning scenario and

the sensors we use for individual learners do not

generate enough data for a high-quality self-learning

system and, on the other hand, we chose to keep the

adaptation mechanisms transparent for learners in the

sense of an "open learner model". We will take up this

issue in the conclusion section again.

3 INSTRUCTIONAL DESIGN

AND SYSTEM

IMPLEMENTATION

Starting in the autumn semester of 2016/17, we have

carried out a two-year field study to implement the

above-mentioned approach. For this we used the

framework of the study module "Mathematics,

Statistics and Operation Research" and our

university's standard student platform (Moodle). This

course covers concepts, terms and methods of one-

dimensional analysis. The entire module is organized

in a blended learning format. In addition to the

participation in five face-to-face sessions, there is a

high proportion of self-study, which consists of a mix

of online and off-line phases. The learning platform

offers students the opportunity to complete voluntary

online task sets that have been modified as part of an

adaptive instructional design compared to non-

adaptive, poorly interactive ones foreseen in the

classic form of the course. The students were enabled

to work on the modified tasks for the first time in the

autumn semester 2017/18.

Distance students in general and students at our

university specially tend to have very different

previous knowledge and different strategies to

acquire knowledge, depending on their education or

professional experience. Accordingly, we supported

learners with lower current knowledge levels by

adapting additional learning support without

hindering those with more knowledge through this

additional support. The learning process itself is

constantly adapted based on a theory-led, rule-based

adaptation mechanism to ensure the optimal cognitive

load during the completion of tasks. As explained

previously the appropriate learning support delivered

to the student was defined by four components: the

sensor determines is a point has been achieved, the

analyser sums up the point total, the controller

determines if a specific threshold has been reached

and the presenter displays recommendations and

other objects of learning support. Our individualised

support focuses on three elements:

The first element (initial sensor) is a first

knowledge determination, consisting of a set of

standard exercises that students complete at the start

of the course. Based on the performance in this

assessment and a given threshold score, the learners

are divided into two groups, “novice" and "expert".

Depending on the score the first task of the set appears

in a guided (high learning support) or an unguided

(low learning support) version.

The second element (step loop) is used to measure

the current level of knowledge within a task and to

determine the appropriate learning support. In this

second element, the default values are determined on

the basis of a specification by experts, taking into

account the difficulty of the different tasks. When

learners reach or exceed the threshold value, i.e. have

(partially) answered a question correctly, they receive

a different feedback than when they receive an

incorrect answer and fall below the threshold value.

Such feedback is given after each step in the task.

This error-sensitive feedback includes appropriate

advice depending on whether there are visible gaps in

knowledge or misinterpretations that can be

characterized by individual wrong answers (cf. for

example Goldberg et al., 2015). Such adaptive

feedback prompts serve to clarify possible

misunderstandings of learners as quickly as possible,

for example by reminding them of forgotten

information (Durlach and Ray, 2011).

The third element, the task loop, consists of both

standard tasks and transfer tasks. The standard tasks

are used to assess to ability to solve a particular

problem, while the transfer task has two objectives:

On the one hand, the transfer task aims to determine

whether a particular problem has been understood and

can be solved in its unguided form (see vertical

transfer), on the other hand, it aims to evaluate

whether the acquired problem-solving knowledge of

a previous basic task can be applied to a similar task

Simple and Effective: An Adaptive Instructional Design for Mathematics Implemented in a Standard Learning Management System

119

on the same issue (see horizontal transfer; van Eck

and Dempsey, 2002). Within each task set, the system

recommends which task a learner should tackle next

and in which form (guided/non-guided). The guided

version includes numerous small solution steps, while

the unguided version is composed of few solution

steps.

To promote the acceptance and motivation of

learners, we chose a mixed form of adaptation

(system controlled) and adaptability (learner

controlled). This means that the learners receive

recommendations as to which tasks (and in which

form) they should ideally complete according to the

current level of knowledge. The learner always has

the choice whether to comply with these

recommendations or not. The recommendations

themselves are integrated into the task feedback. At

the same time, the sensor data (current state of

knowledge) is also made available to the learners in a

clear and concise way to promote their own self-

assessment skills and the acceptance of the

recommendations (see open learning models, e.g.

Long and Aleven, 2017; Suleman et al., 2016).

4 ANALYSIS

In order to investigate the impact of our instruction

design (based on the adaptation of task difficulty in a

mathematical course) on learning progress, we

concentrate in a first step on the relationship of online

activity and learning progress and in the second step

on the connection between previous knowledge and

learning progress in a comparison of an adaptive and

a non-adaptive course module. To achieve this goal,

we have formulated two hypotheses for our

exploratory investigations:

: Students who actively perform the tasks of

adaptive instruction design have a higher learning

progress than those who do not actively engage in

these tasks.

H2: Regardless of pre-knowledge, adaptive

design leads to higher learning progress for students

who are actively engaged in learning tasks.

All statistical operations were performed with

IBM SPSS Statistics 23.

4.1 Object of Investigation and

Subjects

As we have already reported, for the use of adaptive

tasks with a recommendation system in our

investigation we chose the mathematics module

"Mathematics, Statistics and Operation Research (in

the following always named MSOR1)". The module

is offered each autumn semester at our university. We

chose this module, as it can be called a “problem

module”. It is the first math module in the university

program and has a high failure rate.

In each semester the students are divided into

seven or eight classes. Each class has its own online

course. At our university all courses base on a

blended learning concept which includes 80%

distance study and 20% interaction with tutor either

online or face to face. The classes allow students, who

usually work in a profession, to choose the best place

(and date) for the face-to-face events. This division

has no influence on the module content or the online

part of the course.

In the autumn semester 2017/18 were implemented

84 adaptive tasks in the module MSOR1. These tasks

cover each learning goal several times. However, not

all tasks have to be completed by a student. A good

student, for example may only need to complete 18

adaptive tasks after having successfully completed the

first knowledge assessment (initial sensor). This is if he

always follows the recommendations. With these 18

tasks he will have worked on each learning goal once.

So the principle differences between the module of

2016/17 and the 2017/18 one are the additional

adaptive tasks that were implemented. The remaining

module content was the same. The data of 288

students was used for this analysis. 143 students from

the adaptive MSOR1 autumn semester 2017/18

module and 145 students from the non-adaptive

MSOR1 of the autumn semester 2016/17 (see table

1). The data from this second module was only used

for the comparison of learning progress.

Table 1: Dataset.

semester n

Non-adaptive Course (MSOR1, AS 2016/17) 145

Adaptive Course (MSOR1, AS 2017/18) 143

overall 288

4.2 Procedure

To start off we compared the students' learning

progress in the module MSOR1 of the autumn

semester 2017/18. We looked at the students’ log files

with focus on the number of tasks completed. Some

students did not use the adaptive tasks, but other

students worked very intensively with the tasks. Thus,

we decided to take the group of students who did not

use the adaptive tasks as a control group for this

module. We will compare their learning progress with

CHIRA 2018 - 2nd International Conference on Computer-Human Interaction Research and Applications

120

the students, who use the adaptive tasks for their

learning.

In a second step will also compare the learning

progress between the adaptive course and the non-

adaptive course (MSOR1 AS 2017/18 and AS 2016/17

respectively). To achieve this we will focus on learning

progress. Finally we will compare the two courses in

regard to previous knowledge and online activity.

4.3 Online Activity

Taking into account the number of tasks completed,

we divide the participants into three groups to define

different activity groups of the adaptive module (table

2). The first group (the control group) is classified as

"Inactive". These participants have completed a

maximum of three adaptive tasks online, this means

less than one per topic. The second group are referred

to as "moderate active". These students worked on

four to sixteen adaptive tasks. Sixteen completed

tasks are just under the minimum number of 18 tasks

with which a (good) student needs to address all

learning objectives. The third group were named

"Active". These students performed at least 17

adaptive tasks.

Students were free to choose whether or not to

work on the tasks. While working on the tasks, they

were also allowed to freely decide whether to follow

the recommendations of the system and the learning

support or not.

In our analysis we only account for completed

tasks because the recommendation made on task loop

is only given after a completed task.

Table 2: Activity groups with students per group (n), mean

and standard deviation of tasks completed.

group n mean

tasks

Inactive 68 0.46 0.94

Moderate Active 41 9.00 3.22

Active 34 30.09 14.8

overall 143 10.0 13.95

The number of tasks completed by a student in the

module has a high correlation (Pearson's r = .926)

with the total online activity in the module (number

of logs). From the number of tasks processed, we

therefore assume a high level of online activity.

4.4 Pre-Knowledge, Learning Progress

and Online Activity

In the following step we try to explain the relationship

between the online activity and the learning progress

in the adaptive module. For this purpose learning

progress was defined as the difference between the

results of the pre-knowledge test and the final test,

both standardized to 100.

Table 3: Learning progress of groups.

group n mean

learning

progress

learning

progress

Inactive 22 8.40 29.11

Moderate Active 36 21.49 32.32

Active 32 32.36 22.05

overall 90 22.15 29.40

Table 3 shows the distribution of the learning

process among the three groups. Only students who

completed both the pre-knowledge assessment and

the final test could be included in the analysis.

A t-test was performed that shows a significant

difference with regard to learning progress between

the "Inactive" and the "Active" group (t (52) = -3.442,

p = .001, n = 54). The variance homogeneity, tested

with Levene’s test, was given (F (1, 52) = 1.126, p =

.293, n = 54). The comparison of the “Moderate

Active” group with the “Inactive” and the “Active”

group failed to show a significant difference in the t-

test (t (56) = -1.552, p = .126, n = 58) and (t (66) =

-1.600, p = .114, n = 68 respectively). Variance

homogeneity, as tested with Levene’s test, was given

for both tests (F (1, 56) = 0.303, p = .584, n = 58) and

(F (1, 66) = 3.196, p = .078, n = 68 respectively). The

results show that, in line with our first hypothesis

), more online activity leads to more progress for

students who actively participate in the adaptive

learning module than for those who do less. It is also

to note, that the non-adaptive course of the autumn

semester 2016/17 was non-interactive and did not

allow online activity. In view of this fact, no direct

comparison between the adaptive and non-adaptive

course modules is possible with regard to the

correlation between learning progress and online

activity.

The same pre-assessment and a comparable final

test were used in both courses, allowing for

comparison of learning progress of both modules.

The comparability of the final test was determined by

a comparison of the pass-grades students obtained in

this final test. The mean values and the SD are close

to each other (autumn semester 16/17: Mean = 5.07,

SD = .644. Autumn semester 17/18: Mean = 5.24, SD

= .707.). This allows the learning progress of different

levels of previous knowledge i. e. different starting

positions to be compared between the courses.

Students were divided into “novices” (less than 50%

correct) and “experts” (more than 50% correct)

Simple and Effective: An Adaptive Instructional Design for Mathematics Implemented in a Standard Learning Management System

121

depending on the achieved points in the initial

assessment.

Table 4 and 5 show the mean of the initial

assessment (pre-knowledge test) and the mean score

on the final test separated by semester.

Table 4: Mean pre-knowledge test (standardized to 100).

semester n mean pre-

knowledge

Non-adaptive

Course (MSOR1,

AS 2016/17)

92 54.83 18.48

Adaptive Course

(MSOR1, AS

2017/18)

103 45.96 23.93

Table 5: Mean final test (standardized to 100).

semester n mean

final test

SD note

final test

Non-adaptive

Course (MSOR1,

AS 2016/17)

124 56.67 25.59

Adaptive Course

(MSOR1, AS

2017/18)

118 61.82 31.14

A t-test showed a significant difference in the

previous knowledge test between MSOR1 HS16/17

and MSOR1 HS17/18 group (t (189.149) = 2.911, p

= .004, n = 195). The variance homogeneity, checked

with Levene's test, was not given (F (1, 193) = 7.252,

p = .008, n = 195), therefore the corrected t-value was

chosen.

The t-test did not show any significant difference

between both semesters on the final test (t (226.681)

= -1.403, p = .162, n = 242). The variance

homogeneity, also checked with Levene's test, was

not given (F (1, 240) = 12.135, p = .001, n = 242),

therefore the corrected t-value was chosen. This

results shows, that the final tests had comparable

difficulties.

In a further step the course participants of adaptive

course (MSOR1 AS 2017/18) were divided into six

groups with regard to online activity and previous

knowledge. To compare the courses (adaptive vs.

non-adaptive), the two groups (“novices” and

“experts”) of the traditional course from the autumn

semester 2016/17 were also taken into account. The

results of the learning progress in the corresponding

eight groups are listed in Table 6.

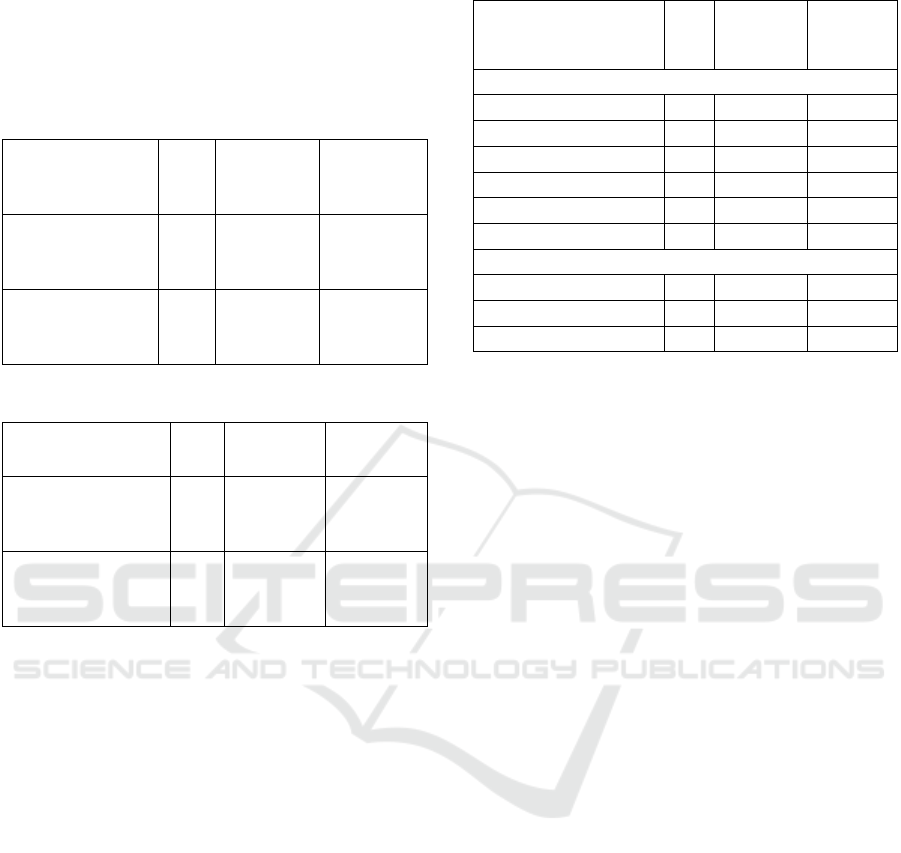
Table 6: Pre-knowledge level and learning progress.

group n

mean

learning

progress

learning

progress

Adaptive Course, MSOR1 , AS 2017/18

Active Novices 12 49.23 21.39

Moderate Act. Nov. 19 29.11 35.55

Inactive Novices 14 16.19 30.76

Active Experts 20 22.24 15.52

Moderate Act. Exp. 17 12.97 26.79

Inactive Experts 8 -5.24 21.24

Non-adaptive Course, MSOR1, AS 2016/17

Novices 34 19.04 21.64

Experts 51 -12.12 28.73

overall 175 11.56 31.65

In the following analysis we excluded the group

of inactive novices and inactive experts of the

adaptive course, since the non-adaptive course is used

as a control condition compared to the adaptive

course. We applied a one-sided ANOVA with

Tamhane post-hoc testing assuming unequal

variances, as the variance homogeneity tested with

Levene’s test was not given (F (7, 167) = 3.467, p =

.002, n = 175). The one-sided ANOVA shows

significant group effects (F (7, 174) = 11.979, p <

0.001, n = 175). The post hoc test leads to significant

differences between active Novices (Mean = 49.23)

of the adaptive course and the Novices (Mean =

19.04) of the non-adaptive course (p = .013) as well

between the active Experts (Mean = 22.24) of the

adaptive course and the Experts (Mean = -12.12) of

the non-adaptive course (p < 0.001). These results

indicate in line with our second hypothesis (H

) that

for students who are actively involved in adaptive

learning tasks regardless of their pre-knowledge,

adaptive design leads to a higher level of learning

progress compared to non-adaptive design. However,

we also have to note that no significant differences

were found between moderate active novices (Mean

= 29.11) of the adaptive course compared to novices

(Mean = 19.04) of the non-adaptive course (p =

1.000) and also between the moderate active experts

(Mean = 12.97) of the adaptive course and the experts

(Mean = -12.12) of the non-adaptive course (p =

.072). From our point of view, this result indicates

that a certain online activity level is necessary for the

adaptive instructional design to be effective.

In addition, we have found a significant difference

between the learning progress of active novices

(Mean = 49.23) and active experts (Mean = 22.24) of

the adaptive course (p = .035). A difference was also

found in the non-adaptive course for the Novices

CHIRA 2018 - 2nd International Conference on Computer-Human Interaction Research and Applications

122

(Mean = 19.04) and the Experts (Mean = -12.12) (p =

.001). This can be understood by the novices having

a larger learning progress than the experts in both

courses.

Besides the significant differences mentioned

here, however, we also point out that the differences

between the active novices (Mean = 49.23) and the

inactive novices (Mean = 16.19) and between the

active experts (Mean = 22.24) and the inactive experts

(Mean = -5.24) cannot be shown as significant

(between novices p = .102 and between experts p =

.192) despite the high differences between the mean

values. We assume that large individual differences

and the real small number of test persons play a role

here.

5 DISCUSSION OF THE FIRST

EXPLORATIVE RESULTS

In this article we presented an adaptive instruction

design which was implemented in a standard learning

management system as a relatively simple concept.

The theoretical part of the instruction refers to the

Cognitive Load Theory and the Expertise Reversal

Effect. On this basis we developed adaptive task sets

and combined them with a recommendation system.

The practical application took place in a mathematics

module (AS 2017/18) at our university.

The first results on effects related to students'

different prior knowledge, online activity and

learning progress show some positive effects of the

adaptive design used, although not all results are

unambiguously. We have also found some unclear

results, such as the insignificant differences between

the active and inactive novices and between the active

and inactive experts in the adaptive course, even

though there are very high differences in the mean

values. Hence it has also become apparent that some

further clarifications are necessary and will also

require further in-depth research.

All in all the students from the adaptive course

scored significantly worse in the pre-knowledge test

than their fellow students from the non-adaptive

course. This is not due to the adaptive design, as at

the time when the students fill out the pre-knowledge

test no adaptive measures have been taken. But rather

simply that one year students had a higher starting

level than the next. It is also evident that at the end of

the adaptive course more students (54.2 %) passed

this examination on their first attempt than after the

non-adaptive course (37.0 %), despite a similarly

difficult final examination.

As mentioned previously, the results show a clear

improvement in learning progress with increasing

online activity in which students actively work

through online tasks. The better results of both the

novices and the experts with high online activity

indicate this. However, this result cannot

unequivocally be attributed to the instructional

design. Higher online activity could lead to better

results independently of learning design. Or the better

results could effectively be due to the instructional

design and the compliance of the recommendations.

To clarify this question further investigations are

required. Furthermore, the significant differences can

only be seen in the comparison of very active students

and inactive students. This means that a certain level

of activity is necessary. In fact, the question arises as

to why moderately active participants did not benefit

significantly from the instructional design but also did

not differ significantly from the active participants. It

is possible, that they do benefit a bit, but by not

committing to the recommendations the benefit is

only limited. We also found that 47.6 % of students

(in the AS 2017/18) were not active online.

Unfortunately, it was not possible in our study to

control further learning activities (such as learning

offline, face to face discussions, etc.). These learning

activities could have had an impact as well.

Further, we found a significant difference

between novices and experts in terms of learning

progress in both the active group of the AS 2017/18

group and the AS 2016/17 group (control). In both

instances the novices showed a more prominent

learning progress. The interpretation that this cannot

be attributed to adaptive tasks can be justified, as the

same difference can be seen in both adaptive and non-

adaptive courses. In this context, however, it would

be interesting to examine more precisely the learning

paths of the individual students in order to determine

whether the learning progress can be traced back,

among other things, to more success or more and

earlier positive feedback, especially in the case of the

novices and thus also be attributed to motivational

factors. Another possible explanation could be, that

the experts started at a point where their potential to

improve was just too small. Such a ceiling effect

would lead to similar result.

6 CONCLUSIONS

Returning to our three-part research question,

whether it is possible to implement an adaptive

learning system based on a cognitive learning

approach in a classical learning environment (1), to

Simple and Effective: An Adaptive Instructional Design for Mathematics Implemented in a Standard Learning Management System

123

what extent the cognitive factors and technical

components mentioned in previous parts contribute to

improving learning progress, taking into account the

design of the corresponding instructional design (2),

and which possibilities this opens up and which limits

are set (3), the following conclusions can be drawn:

The instructional design used in this project refers

to findings of cognitive load theory and the associated

Expertise Reversal Effect. This approach points out

that the teaching support helpful to beginners (low

level of knowledge) can be superfluous or even

harmful to experts (high level of knowledge) and vice

versa (Kalyuga, 2007a, b). We have shown that

adaptive interventions used for the adaptive learning

design of online tasks in mathematics are possible.

The consideration of the difficulty of the tasks and the

previous knowledge, as well as the students'

intermediate solutions in the step loop and the

distinction between guided/unguided tasks with a

correspondingly elaborated feedback, as selected

here, seems to represent a useful and achievable

adaptation approach (see e.g. also Brunstein et al.,

2009; Hsu et al., 2015; instructions with feedback:

e.g. van der Kleij et al., 2015). However, during the

development of the design we were also able to note

that there are numerous other possibilities for design

adaptations and interventions. In this respect, there is

the option of further designs can be varied or

extended. Some of these methods are much more

complex in concept and design, but potentially bring

further advantages. For example, the differentiation

with regard to the level of knowledge and the

associated level of didactic guidance could be refined

(e.g. adding a medium level of competence and a

medium level of didactic guidance). In this sense we

have deliberately concentrated on a rather easy to

implement version. Of course there is no standard

optimal adaptive teaching design in the field of

adaptive learning, but the specific learning objectives

and characteristics of the teaching and learning

environment should be taken into account. The

adaptive, elaborate feedback used here is suitable for

learning objects where certain misunderstandings are

based on false answers and can be recognized. The

distinction between guided and unguided teaching

according to the level of knowledge seems to be easy

to implement, especially for tasks in mathematics

teaching, which require basic previous knowledge.

By confirming our two hypotheses, we were also

able to show that high online activity leading to clear

learning progress can be realized with both a low and

a high level of pre-knowledge. As already mentioned,

we have not yet evaluated data on the acceptance and

use of the recommendations. In principle, the students

were free to decide whether they would follow the

recommendations contained in the feedback on the

tasks (and on the previous knowledge test). It was

also up to the students to decide whether they want to

perform a task one time, perform it several times or

skip it.

Based on our theoretical assumptions about the

concept of the adaptive design, a significant learning

effect should be demonstrated for students who have

followed the recommendations. In principle, one can

assume that learners following such

recommendations invest more learning effort or

practice more in a well thought-out adaptive system.

Therefore, it should also be carefully examined

whether more learning effort and practice goes hand

in hand with greater learning efficiency. However, it

must be taken into account that the design of the user

interface has a considerable influence on the learning

behaviour and thus also on the learning progress of

the students. In particular, the presentation of learning

content and the handling of the learning system, lead

to an extraneous cognitive load (Sweller et al., 2011).

In fact, we have not taken the relevant questions into

account in this study. In our further research,

however, we will look into these issues more closely.

In addition to the Cognitive Load Theory (CLT) for

instance various findings from the application of

Cognitive theory of Multimedia learning (CTML) can

be used (see for an overview Mayer, 2009).

Overall, we have repeatedly been challenged by

the fact that technological feasibility alone is no

guarantee of the didactic quality of the system. As

such, it is therefore appropriate to check and, if

necessary, optimise the functioning of implemented

components using, for example, empirical learning

analytics for the purposes of quality assurance as for

instance the measurement performance of the sensors

(e.g. normal distribution of the number of points

reached in a task, degree of difficulty of the task, etc.)

and dependent threshold values are fundamental for

the quality of the adaptation system. Although not

shown in this paper due excessive length, we

validated the measurement performance of the

sensors in various smaller test runs and the non-

adaptive course which was carried out in the autumn

semester 2016/17. Another element for measuring the

accuracy of sensors is the awareness of the students

in carrying out seriously the assessments. A problem

for a reliable and valid measurement is that it requires

a careful and serious completion of the tasks by the

users. Failure to do so (e.g. quick or unenthusiastic

clicking on answer options without proper thinking or

trial-and-error strategies) can reduce the reliability of

the adjustment basis and thus the informative value of

CHIRA 2018 - 2nd International Conference on Computer-Human Interaction Research and Applications

124

the entire adjustment process. However, it seems

difficult to force a serious completion of the tasks

when time-consuming sensors are connected with

relatively high mental effort. Automatic sensors (such

as face scanners or eye-trackers), which will probably

be available in everyday learning situations in the

future, could solve this problem, since no significant

additional time and effort is then required for learners

to obtain valid measurements. Such "objective"

measurement parameters would function relatively

autonomously. A quick recognition of inappropriate

(unscrupulous) behaviour would then be possible and

instructive interventions could be displayed.

Taking up the third part of our research question,

we note that there is currently a controversial

discussion about the way adaptive learning systems

are controlled. In the concept presented here, we

applied a theory-based, rule-based adaptation

mechanism and avoided the frequently propagated

self-learning mechanism of systems based on

artificial intelligence. One reason for this is that

simple, theory-based mechanisms are generally

understandable for learners if the mechanisms are

clearly communicated (Long and Aleven, 2017;

Suleman et al., 2016). They can also promote

secondary learning objectives such as self-assessment

or self-regulation by learners. Mechanisms acquired

purely from data technology are often less systematic

and logically difficult for learners to understand,

since they cannot be assigned to a specific didactic

theory. Another reason against self-learning

mechanisms was our limited data volume per course

module with approx. 100 students. The debate on

whether the control mechanism should be rule-based

or self-learning is fundamental and advocates of self-

learning systems currently seem to dominate the

literature. For the reasons mentioned above, careful

consideration is necessary to determine in which

learning scenarios and for which learning objectives

rule-based or self-learning control mechanisms are to

be used. In our case it would have made less sense to

control the selection of our adaptive, elaborate

feedback in the step loop by artificial intelligence,

since the formulation of the elaborated feedback itself

is based on theory-led rules. Essa (Essa, 2016), for

example, argues that artificial intelligence generally

seems unsuitable for a step loop adjustment. A

combination of rule-based systems with artificial

intelligence could also be a useful mechanism.

Further research is needed to obtain concrete

information on the advantages and disadvantages of

the various control mechanisms.

Finally, we hope that the work presented here will

help bridge the gap between research and practice and

we would like to use our experience to motivate

university and distance teachers to test the

implementation of rule-based, adaptive designs.

ACKNOWLEDGEMENTS

We would like to thank the many students who

actively worked in the two course modules and gave

valuable feedback on the development of adaptive

instructional design. Dr. Stéphanie McGarrity from

the Institute for Open, Distance and eLearning

Research (IFeL) of the Swiss Distance University of

Applied Sciences (FFHS) for proofreading and her

valuable advice.

REFERENCES

Bergamin, P. B., Werlen, E., Siegenthaler, E., Ziska, S.,

2012. The relationship between flexible and self-

regulated learning in open and distance universities. In

The International Review of Research in Open and

Distributed Learning, 13(2), 101-123. https://doi.org/

https://dx.doi.org/10.19173/irrodl.v13i2.1124

Boticario, J. G., Santos, O. C., 2006. Issues in developing

adaptive learning management systems for higher

education institutions. In International Workshop on

Adaptive Learning and Learning Design, Adaptive

Hypermedia, 2006. Ireland.

Brunstein, A., Betts, S., Anderson, J. R., 2009. Practice

enables successful learning under minimal guidance. In

Journal of Educational Psychology, 101(4), 790802.

https://doi.org/10.1037/a0016656

Durlach, P. J., Ray, J. M., 2011. Designing adaptive

instructional environments: Insights from empirical

evidence. Technical Report 1297. Arlington, VA. In

United States Army Research Institute for the

Behavioral and Social Sciences.

Essa, A., 2016. A possible future for next generation

adaptive learning systems. In Smart Learning

Environments, 3.

https://doi.org/10.1186/s40561-016-0038-y

FitzGerald, E., Kucirkova, N., Jones, A., Cross, S.,

Ferguson, R., Herodotou, C., Hillaire, G., Scanlon, E.,

2017. Dimensions of personalisation in technology-

enhanced learning: A framework and implications for

design. In British Journal of Educational Technology,

(in press). https://doi.org/10.1111/bjet.12534

Goldberg, B., Sinatra, A., Sottilare, R., Moss, J., Graesser,

A., 2015. Instructional management for adaptive

training and education in support of the US Army

learning model – Research outline. In Army Research

Lab Aberdeen.

https://doi.org/10.13140/RG.2.1.3464.6482

Hsu, Y., Gao, Y., Liu, T. C., Sweller, J., 2015. Interactions

between levels of instructional detail and expertise

Simple and Effective: An Adaptive Instructional Design for Mathematics Implemented in a Standard Learning Management System

125

when learning with computer simulations. In

Educational Technology and Society, 18(4), 113–127.

Johnson, L., Adams Becker, S., Cummins, M., Estrada, V.,

Freeman, A., Hall, C., 2016. NMC Horizon Report:

2016 Higher Education Edition. Austin, Texas: The

New Media Consortium.

Kalyuga, S., 2007a. Enhancing instructional efficiency of

interactive e-learning environments: A cognitive load

perspective. In Educational Psychology Review, 19(3),

387-399.

https://doi.org/10.1007/s10648-007-9051-6

Kalyuga, S., 2007b. Expertise Reversal Effect and its

implications for learner-tailored instruction. In

Educational Psychology Review, 19(4), 509-539.

https://doi.org/10.1007/s10648-007-9054-3

Kalyuga, S., 2011a. Cognitive load in adaptive multimedia

learning. In R. A. Calvo, S. K. D’Mello (Eds.), New

perspectives on affect and learning technologies (p.

203-2015). New York: Springer.

Kalyuga, S., 2011b. Cognitive Load Theory: How many

types of load does it really need? In Educational

Psychology Review, 23(1), 1-19.

https://doi.org/10.1007/s10648-010-9150-7

Kalyuga, S., Singh, A.-M., 2016. Rethinking the boundaries

of Cognitive Load Theory in complex learning. In

Educational Psychology Review, 28(4), 831-852.

https://doi.org/10.1007/s10648-015-9352-0

Kalyuga, S. and Sweller, J., 2005. Rapid dynamic

assessment of expertise to improve the efficiency of

adaptive e-learning. In Educational Technology

Research and Development, 53(3), 83-93.

https://doi.org/10.1007/BF02504800

Kalyuga, S., Ayres, P., Chandler, P., Sweller, J., 2003. The

Expertise Reversal Effect. In Educational Psychologist,

38(1), 23-31.

https://doi.org/10.1207/S15326985EP3801_4

Kirschner, P., van Merriënboer, J. J. G., 2013. Do learners

really know best? Urban legends in education. In

Educational Psychologist, 48(3), 169-183.

https://doi.org/10.1080/00461520.2013.804395

Lee, C. H., Kalyuga, S., 2014. Expertise Reversal Effect

and its instructional implications. In V. A. Benassi, C.

E. Overson, C. M. Hakala (Eds.), Applying science of

learning in education: Infusing psychological science

into curriculum (pp. 31-44). American Psychological

Association - STP.

Long, Y., Aleven, V., 2017. Enhancing learning outcomes

through self-regulated learning support with an open

learner model. In User Modeling and User-Adapted

Interaction, 27(1), 55-88.

https://doi.org/10.1007/s11257-016-9186-6

Mayer, R. E., 2009. Multimedia learning (2nd ed). New

York: Cambridge University Press.

Murray, M. C., Pérez, J., 2015. Informing and performing:

A study comparing adaptive learning to traditional

learning. In Informing Science, 18(1), 111-125.

Nakić, J., Granić

, A., Glavinić, V., 2015. Anatomy of

student models in adaptive learning systems: A

systematic literature review of individual differences

from 2001 to 2013. In Journal of Educational

Computing Research (Vol. 51).

https://doi.org/10.2190/EC.51.4.e

Paas, F., Renkl, A., Sweller, J., 2003. Cognitive Load

Theory and instructional design: Recent developments.

In Educational Psychologist, 38(1), 1-4.

https://dx.doi.org/10.1207/S15326985EP3801_1

Scanlon, E., Sharples, M., Fenton-O’Creevy, M., Fleck, J.,

Cooban, C., Ferguson, R., Cross, S., Waterhouse, P.,

2013. Beyond prototypes: Enabling innovation in

technology-enhanced learning. Open University,

Milton Keynes.

Somyürek, S., 2015. The new trends in adaptive educational

hypermedia systems. In The International Review of

Research in Open and Distributed Learning, 16(1).

https://doi.org/https://dx.doi.org/10.19173/irrodl.v16i1

.1946

Suleman, R. M., Mizoguchi, R., Ikeda, M., 2016. A new

perspective of negotiation-based dialog to enhance

metacognitive skills in the context of open learner

models. In International Journal of Artificial

Intelligence in Education, 26(4), 1069-1115.

https://doi.org/10.1007/s40593-016-0118-8

Sweller, J., 1988. Cognitive load during problem solving:

Effects on learning. In Cognitive Science, 12(2), 257-

285.

Sweller J., Ayres P., Kalyuga S., 2011. Intrinsic and

Extraneous Cognitive Load. In Cognitive Load Theory.

Explorations in the Learning Sciences, Instructional

Systems and Performance Technologies, vol 1.

Springer, New York, NY

van der Kleij, F. M., Feskens, R. C. W., Eggen, T. J. H. M.,

2015. Effects of feedback in a computer-based learning

environment on students’ learning outcomes: A meta-

analysis. In Review of Educational Research, 85(4),

475-511.

https://doi.org/10.3102/0034654314564881

van Eck, R., Dempsey, J., 2002. The effect of competition

and contextualized advisement on the transfer of

mathematics skills in a computer-based instructional

simulation game. In Educational Technology Research

& Development, 50(3), 23-41.

https://doi.org/10.1007/BF02505023

van Merriënboer, J. J. G., Sluijsmans, D. M. A., 2009.

Toward a synthesis of cognitive load theory, four-

component instructional design, and self-directed

learning. In Educational Psychology Review, 21(1), 55-

66.

https://doi.org/10.1007/s10648-008-9092-5

Wauters, K., Desmet, P., van Den Noortgate, W., 2010.

Adaptive item-based learning environments based on

the item response theory: Possibilities and challenges.

In Journal of Computer Assisted Learning, 26(6), 549-

562.

https://doi.org/10.1111/j.1365-2729.2010.00368.x

Zimmermann, A., Specht, M., Lorenz, A., 2005.

Personalization and context management. In User

Modeling and User-Adapted Interaction, 15(3), 275-

302.

https://doi.org/doi:10.1007/s11257-005-1092-2

CHIRA 2018 - 2nd International Conference on Computer-Human Interaction Research and Applications

126