State- and Uncertainty-observers-based Controller for a Class of T-S

Fuzzy Models

Hugang Han, Daisu ke Hamasaki and Jiaba o Fu

Graduate School, Prefectural University of Hiroshima, Hiroshima, Japan

Keywords:

T-S Fuzzy Model, State Observer, Uncertainty Observer, Nussbaum-type Function, Adaptive Law, LMIs.

Abstract:

A control system design based on the T-S fuzzy model with uncertainty is considered in this paper. At ﬁrst,

state observer is developed to estimate the state properly despite the existence of the uncertainty. Then, un-

certainty observer is derived using the estimated state. Finally, a controller based on the observers is proposed

in an effort to counteract the inﬂuence of the uncertainty whatever possible. In addition, the Nussbaum-type

function and its relevant properties are used in the controller design to cover the observers’ error and the part

of esti mated uncertainty that is not possibly used through the control matrices. As a result, the closed-loop

control system becomes asymptotically stable.

1 INTRODUCTION

The T-S fuzzy model (Takagi and Sugeno, 1985) is

widely used in the control system design. Because the

consequent of fuzzy rules that compose the T-S fuzzy

model is in the form of the state-space representa tion,

usually the linear system theory can be applied straig-

htforwardly to the T- S fuzz y model-based control sy-

stem design. As a re sult, the co ntrol system stability

will be guaranteed by certain linear matrix inequali-

ties (LMIs), which can be solved by some existing

software packages. Recently, the T-S fuzzy model

has bee n further extended to the so-called polynomial

fuzzy model (Tanaka et al., 200 9; Han et al., 20 17).

However, whatever models ma y be, th ey ar e not more

than a mathe matical description to, usua lly approxi-

mately, describe the dynamics of the concerned sys-

tems. In other words, it seems almost impossible to

form a model immaculately, given that nonlinear sys-

tems are usually considered, and what is more, distur-

bance fr om extern al/internal system, parameters’ per-

turbation and unmodeled dynamics always exist in the

real systems. Such a discre pancy between the concer-

ned system and its model is called uncertainty in this

paper.

The uncertainty may be called different names

such as u nknown input, disturbance in different con-

texts. When it comes to controller desig ns, H

∞

cont-

rol (Wei et al., 2016), adaptive control (Khalil, 2 002;

Han et al., 2001; Liu et al., 2016) are thought to be

very effective ways to dealing with it. Nevertheless,

there is still plenty of room to improve the contr ol per-

formance. For example, when it co mes to H

∞

control

approa c h, the inﬂuence of the uncertainty to the state

is no more than being conﬁned to certain prescribed

indexes.

Recently, uncertainty observer-based control pro-

vides a promising approach to handle the uncertainty

and improve robustness. In the existing works (Han,

2016; H an and Lam, 2015), the observers involved are

designed under the assumption that the uncertainty is

not tim e varying. It is clear that such an assumption

is d ifﬁcult to cope with other cases such as acute time

varying uncertainties. Therefore, observing the un-

certainty at a more general level and involving the es-

timated uncertainty in the controller design to cover

its inﬂuence as much as possible is the fundamental

notion of this paper. However, at ﬁrst, a state obser-

ver is presented for the case whe re the state is una-

vailable. Most of state observers based on T-S fuzzy

models in litera ture (Liu and Zhang, 2003; Cao et al.,

2008; Ch adli and Kar imi, 2013; Wei et al., 2016) are

designed in the tr aditional sense similar to the one ba-

sed on the state-space representation, in which some

techniques such as H

∞

approa c h (Cao et al., 2008) and

adaptive contr ol (Lendek et al., 2 010) are used to co-

ver the uncertainty. Inspired by th e existing works for

the case of unknown input (Darouach et al., 1994; Hui

and Zak, 200 5), the one in this paper adopts a different

structure in which some elaborately designed matri-

ces are introduced so that the uncer tainty has no inﬂu-

ence to the the state observer a t all. Then, uncertainty

Han, H., Hamasaki, D. and Fu, J.

State- and Uncertainty-observers-based Controller for a Class of T-S Fuzzy Models.

DOI: 10.5220/0006940305510559

In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 1, pages 551-559

ISBN: 978-989-758-321-6

551

observer is derived using the estimated state. Finally,

a controller based on the o bservers is proposed in an

effort to counteract the inﬂuence of the unce rtainty

whatever possible. In addition, the Nussbaum-type

function and its relevant properties are used in the

controller design to cover the observers’ error and the

part of estima te d uncertainty that is not possibly used

through the control matrices; as a result, the closed-

loop control system becomes asymptotically stable .

Throu ghout this paper, M

−

denotes the pseudo-

inverse of M ∈ R

m×n

, i.e., a m atrix satisfying the equa-

tion MM

−

M = M, which means M

−

is either the left

pseudo- inverse M

†

= (M

−1

or right pseudo-

inverse M

‡

= M

(MM

)

−1

. It is clear that M

†

M = I

‡

= I

. In addition, k · k, and | · | den ote the p-

norm with p being 2, and 1, respectively.

2 STATE AND UNCERTAINTY

OBSERVERS BASED ON T-S

FUZZY MODEL

Assume th a t a nonlinear system can be repre sented by

the following T-S fuzzy model:

Plant Rule i :

If θ

(t) is M

and···and θ

(t) is M

, then

˙x(t) = A

x(t) + B

u(t) + Dd(t)

y(t) = Cx(t)



(1)

where θ

( j = 1, 2, · · · , n

) is a variable in the an te ce-

dent th at is available; M

(i = 1, 2, . . . , n

), a fuzzy

term corresponding to ith rule; x(t) ∈ R

, the state

vector; u(t) ∈ R

, the input vector; y(t) ∈ R

, the out-

put vector; A

∈ R

n×n

, B

∈ R

n×m

, C ∈ R

p×n

, D ∈ R

n×r

some compatible matrices; d(t) ∈ R

, uncertainty in-

cluding modeling error, external disturbance , unmo-

deled d ynamics and parameter perturbations. In the

model, it is assumed that rank(CD) = r ank(D).

The overall T-S fuzzy m odel is of the following

form accordingly:

˙x(t) =

∑

i=1

(t)



x(t) + B

u(t) + Dd(t)



y(t) = Cx(t)

)

(2)

where θ(t) =



(t) θ

(t)···θ

(t)



(t) =

(θ(t))

∑

i=1

(θ(t))

≥ 0,

∑

i=1

(t) = 1,

(θ(t)) =

∏

j=1

(θ

(t)).

Inspired by the approach of unknown input observer

(UIO), the following state observer is ﬁrst suggested:

State Observer Rule i :

If θ

(t) is M

and···and θ

(t) is M

, then

˙z(t) = F

z(t) + T B

u(t) + G

ˆx(t) = z(t) + Hy(t)



(3)

where z(t) ∈ R

, is the in te rnal state vector of the

observer; ˆx(t) ∈ R

, the estimate of the state x(t);

∈ R

n×n

, T ∈ R

n×n

, G

∈ R

n×p

, H ∈ R

n×p

, the de-

signs parameters to be determined.

The overall observer of the following form accor-

dingly.

˙z(t) =

∑

i=1

(t)



z + T B

u + G



ˆx(t) = z(t) + Hy(t)

)

(4)

From h ere, unless c onfusion arises arguments

such as t, θ will be omitted just for notational con-

venience.

From (4), we have

ˆx = ˙z + HC ˙x

∑

i=1



z + T B

u + G

Cx + HC(A

x + B

u + Dd)



∑

i=1



z + (T + HC) B

+(G

C + HCA

)x + HCDd



. (5)

Deﬁning the estimation error between x and ˆx as:

= ˆx − x (6)

we have

˙e

∑

i=1



z + (T + HC)B

u + (G

C + HCA

+HCDd − A

x − B

u − Dd



∑

i=1



− (A

− G

C − HCA

)x + F

+ (T − (I − HC )) B

u + (HC − I)Dd



∑

i=1



− G

C − HCA

− (A

− G

C − HCA

) ˆx + F

+ (T − (I − HC )) B

u + (HC − I)Dd



∑

i=1



− G

C − HCA

− G

− (A

− G

C − HCA

)(z + Hy) + F

CTDE 2018 - Special Session on Control Theory and Differential Equations

552

+ (T − (I − HC )) B

u + (HC − I)Dd



∑

i=1



− G

C − HCA

− G

C(z + Hy − x)

+ (F

− (A

− G

C − HCA

))z + G

− (A

− G

C − HCA

)Hy + G

CHy

+ (T − (I − HC )) B

u + (HC − I)Dd



∑

i=1



− G

C − HCA

+ (F

− (A

− G

C − HCA

))z

+ (G

− (A

− G

C − HCA

)H)y

+ (T − (I − HC )) B

u + (HC − I)Dd



(7)

where

= G

+ G

. (8)

Let

(HC − I)D = 0 (9)

= A

− G

C − HCA

(10)

= F

H (11)

T = I − HC (12)

then we have

˙e

∑

i=1

. (13)

Therefore, e

converges to zero if F

is a Hurwitz ma-

trix as long as th e relations (8)-(12) are held. Now,

let us elaborate on it. From (9), we have HCD = D.

When rank(CD) = rank(D) holds true, CD is a full

column rank ma trix, a solution H of the e quation is:

H = E (CD)

†

. (14)

Once H is determined, G

in (10) can be obtained by

= Q

−1

(15)

where Q = Q

∈ R

n×n

and M

∈ R

n×p

are decision

parameters in the following LMIs that make F

a Hur-

witz matrix:

Q > 0 (16)

Q + QHCA

− M

+ (A

Q + QHCA

− M

< 0 (17)

for i = 1, 2, ··· , n

The above L MIs follow from the Lyapunov’s stability

theorem by deﬁning a Lyapunov function V = e

Finally, having H and F

in mind, G

, and T can be

straightfor ward ly obtained from (11), and ( 12), re-

spectively. 

After e stablishing the state observer, we move on

to consider how to observe the uncertainty d. As

shown later, there is no necessity to pinp oint d itself,

but the whole term of Dd from the viewpoint of con-

troller design. Letting

= Dd (18)

an observer of D

follows fro m (2):

∑

i=1



ˆx + B



−

ˆx. (19)

Deﬁning the estimation error between D

and

as:

− D

(20)

it is clear that e

→ 0 as long as e

→ 0.

In the following, our interest is how to make most

in controller design. Considering a special case

of the existence of B

−1

, it would be able to design a

controller that is based on a regular control input u

with an extra elemen t such as u − B

−1

to counte-

ract the inﬂuence of D

completely. However, such

a special ca se is h ighly unlikely to happen in the real

system due to the fact that m ≤ n which is the dimen-

sions of th e control matrix B

usually. This implies

that

cannot be used in the controller de sig n at this

stage. Nevertheless, we have to diminish the inﬂu-

ence of M

whatever possible. For this purpose, let us

recall the fo llowing lemma.

Lemma 1. (Baksalary and Kala, 1979) Let B ∈

m×k

, M ∈ R

l×n

, and N ∈ R

m×n

. The equation

BX − MY = N (21)

has a solution X ∈ R

k×n

,Y ∈ R

m×l

, if and only if



I − BB

−





I − M

−



= 0. (22)

If this is the case, the general solution of (21) has the

form

X = B

−

N + B

−

ZM +



I − B

−



W (23)

Y = −



I − B

−



−

+ Z −



I − B

−



ZMM

−

(24)

where W ∈ R

k×n

, Z ∈ R

m×l

being arbitrary. 

It is evident that the condition (22) is held if

M = −I. In this case, (21) admits X = B

−

N an d

Y = −(I = BB

−

)NM

−

as a solution. Therefore, ac-

cording to Le mma 1,

can be divided into the fol-

lowing form:

= B

+ ∆E

(25)

State- and Uncertainty-observers-based Controller for a Class of T-S Fuzzy Models

553

where ψ

= B

†

and ∆E

−B

are a solution

of the equation B

X +Y =

. By doing so, ψ

can be

used in the co ntroller design partially to counteract

the inﬂue nce of D

. However, as a solution of the

equation, in fact there is no guarantee that the magni-

tude of ∆E

, for example ||∆E

||, is less than that of

. In other words, in the case of ||∆E

|| > ||

||,

on the contrary, ψ

used in the controller design will

worsen the inﬂuence of the uncertainty. Therefore, in

order to make sure the effect of the counteraction of

the uncertainty, ψ

in (25) is obtained by

(

†

− B

k ≤ ||

0 otherwise.

(26)

From (2 5) we ob serve that ψ

shares th e same con-

trol matrix B

with the control input u; therefore, it is

the maximum amount to counteract the uncertainty

from the estimated

. It is clear that ψ

= 0 me-

ans that there is no way to use the extracted informa-

tion form

to diminish the inﬂuence of D

at this

stage. The smaller ||∆E

|| is, the better control per-

formance can be expected.

In what follows, let us consider the boundedness

with regard to the estimatio n errors a nd solutions of

equation (25). First, deﬁne

i j

= (F

− A

− e

+ B

(ψ

− ψ

) + ∆E

. (27)

In view of the convergence o f e

and e

along with the

relation in (25), it is clear that Ξ

i j

is bounded.

Let q

i j(k)

(k = 1, 2, ··· , n) be the k-th entr y of the

vector Ξ

i j

∈ R

, i.e.,

i j



i j(1)

i j(2)

··· q

i j(n)



, (28)

and b

i(k)

∈ R

1×m

be the k-th row of B

, i.e.,

i(1)

i(b)

··· b

i(n)

. (29)

Bearing in m ind tha t the boundedness of Ξ

in (27), it

is r easonable to a ssume that there exists a scalar κ > 0

such that

max

j=1∼n



i j(k)



≤ κ · |b

i(k)

|. (30)

In this case, it is easy to che ck that the following ine-

quality holds:

ΓΞ

i j

≤ κ|ΓB

| (31)

where Γ ∈ R

1×n

is an arbitrary vector.

Before starting the controller design, we introduce

the Nussbaum-typ e function (Ye and Jiang, 1998) that

is adopted to de sig n a part of controller in compensa-

tion for the inﬂuence of Ξ

i j

Any continuous function N(ζ) : R → R is a

function of N ussbaum-type functio n if it has the fol-

lowing properties (Nussbaum, 1983):

limsup

z→+∞

N(ζ)dζ = +∞ (32)

liminf

z→+∞

N(ζ)dζ = −∞ (33)

For example, continuous functions ζ

cos(ζ),

sin(ζ) and exp(ζ

)cos(

ζ) are commonly used

as Nussbaum- type functions. Regarding Nussbaum-

type functions, there is the following lemma.

Lemma 2. ( Ye and Jiang, 1998) Let V (·) and ζ(·) be

smooth functions deﬁned on [0,t

) with V (t) ≥ 0, ∀t ∈

[0,t

), N(·) be even smooth Nussbaum- ty pe function.

If the following inequality holds:

V (t) ≤ c



gN(ζ(τ)) + 1



ζ(τ)dτ, ∀t ∈ [0, t

)

(34)

where g is a nonzero constant and c

repre-

sents some suitable constant, then V (t), ζ(t) and

(gN(ζ(τ)) + 1)

ζ(τ)dτ m ust be b ounded on [0, t

Also, the following lemma, which is an alternative

to the Barbalat Lemma (Khalil, 2002), will be used in

the system stability analysis later.

Lemma 3. (Ta o, 1997) A function f : R

→ R is

square integrable, i.e.,

∞

(t)P f (t)dt < ∞, (35)

where P = P

> 0, and has a bounded derivative, then

f (t) → 0, as t → ∞. (36)

3 CONTROLLER DESIGN

Based on the state a nd uncertainty observers, the fol-

lowing controller is proposed.

Controller Rule i :

If θ

is M

and···and θ

is M

, then

u = k

ˆx − ψ

+ φ

(37)

where k

∈ R

m×n

is the feedback control gain that

is o btained by k

= X

−1

with Q = Q

> 0 and

∈ R

m×n

being the d e cision variables of the follo-

wing LMIs:

Q + B

+ QA

+ X

< 0 (38)

for i, j = 1, 2, ··· ,n

;

CTDE 2018 - Special Session on Control Theory and Differential Equations

554

is extracted f rom the estimated uncertainty

(26) in an e ffort to counteract the inﬂuence of the un-

certainty Dd whatever possible; and φ

∈ R

is desig-

ned in compensation for the inﬂuence of Ξ

i j

P ˆx + N(ζ)

∑

j=1

P ˆx + κ · sgn

∑

j=1

P ˆx

(39)

where sgn denotes the sign func tion, κ is given in

(30), P = Q

−1

, N(ζ) ∈ R is a Nussbaum-type function

(Nussbaum, 1983), and

ζ =



∑

i=1

P ˆx



+ κ



∑

i=1

P ˆx



. (40)

The overall fuzzy controller (37 ) is of the follo-

wing form acc ordingly.

u =

∑

i=1



ˆx − ψ

+ φ



. (41)

Substituting (6), (20), (25) and (41) into ( 2), the

closed-loo p control system becomes as follows.

˙x =

∑

i=1



( ˆx − e

) + B

u +

Dd − e



∑

i=1

∑

j=1



+ B

) ˆx − A

+ B

(ψ

− ψ

)

+ B

+ ∆E

− e



. (42)

Substituting (13) and (43) into

ˆx = ˙x + ˙e

which fol-

lows from (6), we have

ˆx =

∑

i=1

∑

j=1



+ B

) ˆx − A

+ B

(ψ

− ψ

)

+ B

+ ∆E

− e

+ F



∑

i=1

∑

j=1



+ B

) ˆx + B

+ Ξ

i j



(43)

where Ξ

i j

is deﬁned in (27).

Bearing in mind that the relatio n in (13) where F

is made to be a Hurwitz matrix, an asymptotically sta-

ble system in (43) does le a d to another asymptotically

stable system in (42). The stability of the system in

(43) is investigated based on the Lyapunov stability

theory. Let us conside r the following quadratic Lya-

punov function candidate:

V = ˆx

P ˆx. (44)

Taking the time derivative of V , we have

V =

ˆx

P ˆx + ˆx

ˆx

∑

i=1

∑

j=1

ˆx



+ B

)

P + P(A

+ B

)



ˆx

+ 2

∑

i=1

∑

j=1

ˆx

P ˆx

+ 2

∑

i=1

ˆx

N(ζ)

∑

j=1

P ˆx + κ · sgn

∑

j=1

P ˆx

+ 2

∑

i=1

∑

j=1

ˆx

PΞ

i j

= − ˆx

H ˆx + 2

∑

i=1

ˆx

∑

j=1

P ˆx + κ · sgn

∑

j=1

P ˆx

− 2

∑

i=1

ˆx

· κ · sgn

∑

j=1

P ˆx

+ 2N(ζ)

ζ+ 2

∑

i=1

∑

j=1

ˆx

PΞ

i j

= − ˆx

H ˆx + 2 (1 + N(ζ))

− 2κ



∑

i=1

ˆx



+ 2

∑

i=1

∑

j=1

ˆx

PΞ

i j

(45)

where

H = −

∑

i=1

∑

j=1



+ B

)

P + P(A

+ B

)



(46)

It is not d ifﬁcult to see that, using (38), H > 0.

Taking the relations (30) and (31) into conside ra-

tion, let us pay attention to the last block in (45).

∑

i=1

∑

j=1

ˆx

PΞ

i j

≤2

∑

i=1

∑

j=1



ˆx



=2κ



∑

i=1

ˆx



(47)

where the fact that α

≥ 0 is used.

Substituting (47) into (45), it follows

V ≤ −ˆx

H ˆx +



1 + N(ζ)



ζ (48)

which also implies

V ≤



1 + N(ζ)



ζ (49)

State- and Uncertainty-observers-based Controller for a Class of T-S Fuzzy Models

555

where the fact that H > 0 is used. Integrating (49), it

follows to we get

V (t) ≤ V (0) +



1 + N(ζ)



ζ(τ)d(τ). (50)

Applying Lemma 2 to (50), we conclude that V (t),

ζ(t), a nd



1 + N(ζ)



ζ(τ)d(τ) must be bounde d.

Again, integrating (48), we have

V (t) ≤V (0) −

(τ)Hx(τ)dτ



1 + N(ζ)



ζ(τ)d(τ). (51)

Because V (t) (as well as V (0)) and



1 +

N(ζ)



ζ(τ)d(τ) are all bo unded, it is evident that

ˆx

(τ)H ˆx(τ)dτ must be bounded. Therefore , we

conclud e that ˆx (t) is square integrable, and that

lim

t→∞

ˆx(t) → 0 according to Lemma 3. 

It is worth no ting that when ψ

and φ

in (37) are

removed:

u =

∑

i=1

x (52)

reduces to the regular parallel distributed compe n-

sation (PDC) controller (Tanaka and Wang, 2001),

where LMIs in (38) are the stability c onditions for

which the uncertainty Dd in (2) is not considered.

4 SIMULATION

Consider the following altered Van der Pol oscillator:

¨z = −z +



1 − z



˙z + u + f

y = 2z + ˙z



(53)

where f denotes uncertainty in the system. In this

simulation, f is assumed to be:

f (t) =











0, if 0 ≤ t < 2

5.3, if 2 ≤ t < 4

0, if 4 ≤ t < 6

−5 + sin(t − 6) + 2 rand(), if 6 ≤ t < 15

3, otherwise

(54)

where rand() is a function that re turns a single uni-

formly random number in the interval (0, 1). T he f

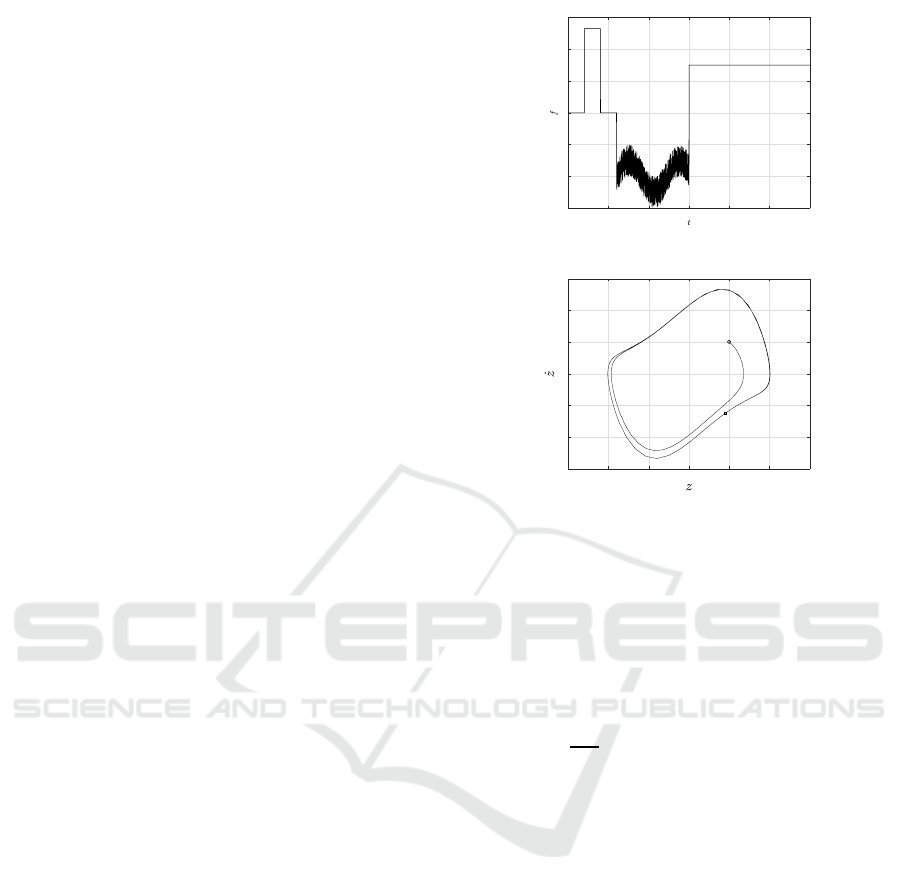
is depicted in Fig. 1. I n the absence of u and f , the

phase plan e z − ˙z is shown in Fig. 2, where the circle

denotes the initial point, the square the end point. It is

clear that the system is unstable without co ntrol.

0 5 10 15 20 25 30

-6

-4

-2

Figure 1: Uncertainty f considered in the system (53).

-3 -2 -1 0 1 2 3

-3

-2

-1

Figure 2: z − ˙z phase plane with u = 0 and f = 0.

The above nonlinear system can be represented by

the following two-rule T-S fuzzy model:

Rule i : If z is M

(z), then

˙x = A

x + B

u + Dd

y = Cx



(55)

where x

= [x

] = [z ˙z], i = 1, 2,

(z) =

(

9−z

, −3 ≤ z ≤ 3

0, otherwise

, M

(z) = 1 − M

(z)



0 1

−1 1



, A



0 1

−1 −8



, B





= B

, C = [

2 1

], D =





and Dd denotes the uncertainty correspon ding to f in

(53). In this paper, the state x is supposed to be una-

vailable; therefore, instead of z = x

in the members-

hip functions, z = ˆx

is used in this simulation.

By solving LMIs in (38) with the help of some

software package, k

and P = Q

−1

are set to be



−0.4286 −2.0 714





−0.4286 6.92 86





(56)

P =



0.0145 0.0058

0.0058 0.0145



. (57)

A Nussbaum-type function , N(ζ) = ζ

cos(ζ) is used

in this simulation. In addition, κ in (39) is set to be

κ = 0.5 + || ˆx||

CTDE 2018 - Special Session on Control Theory and Differential Equations

556

For comparison purposes, the plant (53) in the ab-

sence o f the uncertainty f is ﬁrst controlled by the re-

gular PDC controller (52), the contr ol result is shown

in Fig. 3. It is clear that the regular PDC control-

ler is very effective in this case. However, when the

uncertainty in Fig. 1 is applied to the system, as the

control r esult shown in Fig. 4, the regular controller

is no lo nger able to control the system properly.

-0.4 -0.2 0 0.2 0.4 0.6 0.8 1

-0.7

-0.6

-0.5

-0.4

-0.3

-0.2

-0.1

0.1

0.2

Figure 3: State driven by the regular PDC controller (52)

without the uncertainty.

-4 -3 -2 -1 0 1 2 3 4

-3

-2

-1

Figure 4: State driven by the regular PDC controller (52)

with the uncertainty in (54).

The con trol results by the proposed controller are

shown in Figs. 5∼9. Figs. 5, and 6 depict the re-

sponses of x

(dotted line), its estimate ˆx

(solid line),

and x

(dotted line), its estimate ˆx

(solid line), re-

spectively. We observe that the proposed control is

able to make the states of x

and x

asymptotically

stable, while the state observer (4) is effective to esti-

mate th e real state. Figs. 7, and 8 depict the real un-

certainty D

(1) = 0 (dotted line), its estimate

(1)

(solid line), and D

(2) = f (dotted line), its e stima te

(2) (solid line), resp ectively. It is evident from

them that

follows D

properly. The control input

is shown in Fig. 9. In comparison with Fig. 8, control

input u going in the opposite direction to the u ncer-

tainty f acco rdingly is thought to be mainly co ntribu-

ted by ψ

that is ﬁltered from

by (25) and (26).

Finally, the behaviors of the other parameters, N(ζ),

ζ, are depicted in Figs. 10, and 11, respectively. It can

be seen that all the parameters involved in the system

are bounded.

0 5 10 15 20 25 30

-0.2

0.2

0.4

0.6

0.8

1.2

Figure 5: State x

and its estimate ˆx

driven by the propo-

sed controller (41) along with the observer (4) where the

uncertainty in (54) is applied.

0 5 10 15 20 25 30

-1

-0.5

0.5

1.5

11 11.1 11.2 11.3 11.4 11.5 11.6 11.7 11.8 11.9 12

-0.005

0.005

0.01

0.015

0.02

0.025

Figure 6: State x

and its estimate ˆx

driven by the propo-

sed controller (41) along with the observer (4) where the

uncertainty in (54).

0 5 10 15 20 25 30

-0.01

-0.005

0.005

0.01

0.015

0.02

Figure 7: Uncertainty D

(1) = 0 (dotted li ne) and its esti-

mate

(1) (solid line).

0 5 10 15 20 25 30

-6

-4

-2

11 11.1 11.2 11.3 11.4 11.5 11.6 11.7 11.8 11.9 12

-6

-5

-4

-3

Figure 8: Uncertainty D

(2) = f (dotted line) as shown in

Fig. 1 and its estimate

(2) (solid line).

State- and Uncertainty-observers-based Controller for a Class of T-S Fuzzy Models

557

0 5 10 15 20 25 30

-10

-8

-6

-4

-2

Figure 9: Control input obtained by (41).

0 5 10 15 20 25 30

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

-3

5 7 9 11 13 15 17 19 21 23 25

-6

Figure 10: The behavior of ζ.

0 5 10 15 20 25 30

0.2

0.4

0.6

0.8

1.2

1.4

1.6

-6

5 7 9 11 13 15 17 19 21 23 25

-11

Figure 11: The behavior of N(ζ).

5 CONCLUSIONS

A design of con trol system based on a class of T-S

fuzzy mod els with uncertainty was considered in this

paper. For the case that the state is unavailable, an

state observer was ﬁrstly designed, and then an uncer-

tainty observer was derived using the state estimate.

While it is almost impossible to use the whole esti-

mated uncer ta inty directly in control design, the pa-

per made an effort trying to use it as muc h as possi-

ble to counteract the inﬂuence of the unc ertainty. On

the basis of the observers, a controller was proposed ,

in which the Nussbaum- type function and its relevant

properties were used to make the closed-loop system

asymptotically stable.

ACKNOWLEDGEMENTS

The work described in this paper was partially suppor-

ted by JSPS KAKENHI Grant Number JP 16K06189.

REFERENCES

Baksalary, J. K. and Kala, R. (1979). The matrix equation

ax − yb = c. Linear Algebra Appl., 25:41–43.

Cao, Z., Shi, X., and Ding, S. (2008). Fuzzy

state/disturbance observer design for t-s fuzzy sys-

tems with application to sensor fault estimation. IEEE

Trans. Syst. Man Cybern. B Cybern., 38, No. 3:875–

880.

Chadli, M. and Karimi, H. R. (2013). Robust observer de-

sign for unknown inputs takagi-sugeno models. IEEE

Trans. Fuzzy Syst., 21, Issue 1:158–164.

Darouach, M., Zasadzinski, M., and Xu, S. J. (1994). Full-

order observer for linear systems with unknown in-

puts. IEEE Trans. Automa. Contr., 29:606–609.

Han, H. (2016). An observer-based controller for a class

of polynomial fuzzy systems with disturbance. IEEJ

TEEE C, 11, No. 2:236–242.

Han, H., Chen, J., and Karimi, H. R. (2017). State and dis-

turbance observers-based polynomial fuzzy controller.

Information Sciences, 382-383:38–59.

Han, H. and Lam, H. (2015). Polynomial controller de-

sign using disturbance observer. Journal of Advan-

ced Computational Intelligence and Intelligent Infor-

matics, 19, No.3:439–446.

Han, H., Su, C.-Y., and Stepanenko, Y. (2001). Adaptive

control of a class of nonlinear systems with nonline-

arly parameterized fuzzy approximators. IEEE Trans.

on Fuzzy Systems, 9, No. 2:315–323.

Hui, S. and Zak, S. H. (2005). Observer design for systems

with unknown inputs. Intl. J. Appl. Math. Comp. Scie.,

15, No. 4:431–446.

Khalil, H. K. (2002). Nonlinear Systems. Prentice Hall.

Lendek, Z., Lauber, J., Guerra, T., Babuska, R., and Schut-

ter, B. D. (2010). Adaptive observers for ts fuzzy sy-

stems with unknown polynomial inputs. Fuzzy Sets

and Systems, 161, No. 15:2043–2065.

Liu, X. and Zhang, Q. (2003). New approaches to h

∞

con-

troller designs based on fuzzy observers for t-s f uzzy

systems via lmi. Automatica, 39, Issue 9:1571–1582.

Liu, Y.-J., Gao, Y., Tong, S., and Li, Y. (2016). Fuzzy

approximation-based adaptive backstepping optimal

control for a class of nonlinear discrete-ti me systems

with dead-zone. IEEE Trans. on Fuzzy Systems, 24,

Issue 1:16–28.

Nussbaum, R. D. (1983). S ome remarks on a conjecture in

parameter adaptive control. System & Control Letters,

3:243–246.

Takagi, T. and Sugeno, M. (1985). Fuzzy identiﬁcation of

systems and its applications to modeling and control.

IEEE Trans. Syst., Man, Cybern., 15:116–132.

CTDE 2018 - Special Session on Control Theory and Differential Equations

558

Tanaka, K. and Wang, H. (2001). Fuzzy C ontrol System

Design and Analysis – A Linear Matrix Inequality Ap-

proach. Wiley, New York.

Tanaka, K., Yoshida, H., Ohtake, H., and Wang, H. (2009).

A sum-of-squares approach to modeling and cont-

rol of nonlinear dynamical systems with polynomial

fuzzy systems. IEEE Trans. Fuzzy Syst., 17, No.

4:911–922.

Tao, G. (1997). A simple alternative to the barbalat lemma.

IEEE Trans. Automat. Control, 42, No. 5:698–698.

Wei, X., Wu, Z., and Karimi, H. R. (2016). Disturbance

observer-based disturbance attenuation control for a

class of stochastic systems. Automatica, 63:21–25.

Ye, X. and Jiang, J. (1998). Adaptive nonlinear design wit-

hout a priori knowledge of control direction. IEEE

Trans. Automat. Control, 43, No. 11:1617–1621.

State- and Uncertainty-observers-based Controller for a Class of T-S Fuzzy Models

559