
Cracking KD-Tree: The First Multidimensional Adaptive Indexing
(Position Paper)
Pedro Holanda
1
, Matheus Nerone
2
, Eduardo C. de Almeida
2
and Stefan Manegold
1
1
CWI, Amsterdam, The Netherlands
2
UFPR, Curitiba, Brazil
Keywords:
Multidimensional Range Queries, Database Cracking, Adaptive Indexing, KD-Tree.
Abstract:
Workload-aware physical data access structures are crucial to achieve short response time with (exploratory)
data analysis tasks as commonly required for Big Data and Data Science applications. Recently proposed
techniques such as automatic index advisers (for a priori known static workloads) and query-driven adaptive
incremental indexing (for a priori unknown dynamic workloads) form the state-of-the-art to build single-
dimensional indexes for single-attribute query predicates. However, similar techniques for more demanding
multi-attribute query predicates, which are vital for any data analysis task, have not been proposed, yet. In
this paper, we present our on-going work on a new set of workload-adaptive indexing techniques that focus
on creating multidimensional indexes. We present our proof-of-concept, the Cracking KD-Tree, an adaptive
indexing approach that generates a KD-Tree based on multidimensional range query predicates. It works by
incrementally creating partial multidimensional indexes as a by-product of query processing. The indexes are
produced only on those parts of the data that are accessed, and their creation cost is effectively distributed
across a stream of queries. Experimental results show that the Cracking KD-Tree is three times faster than
creating a full KD-Tree, one order of magnitude faster than executing full scans and two orders of magnitude
faster than using uni-dimensional full or adaptive indexes on multiple columns.
1 INTRODUCTION
Multidimensional range queries (MDRQ) are queries
that select intervals in two or more dimensions of a
multidimensional search space (e.g., a query that se-
arches every person between thirty and fifty years old
and that earns between 100 and 200 thousand dollars
per year). They are very common in OLAP environ-
ments (Ho et al., 1997) and have many exploratory
applications, like: sensor data (Li et al., 2003), ge-
ographic information systems (Alvanaki et al., 2015)
and genomics (Li, 2011). Many benchmarks are com-
posed of at least one MDRQ. For instance, out of
the 22 TPC-H (Poess and Stephens, 2004) benchmark
queries, 6 are MDRQ.
In order to boost MDRQ, many multidimensional
index (MDI) structures have been proposed. For in-
stance: the KD-Tree (Bentley, 1975), R-Tree (Gutt-
man, 1984) and the vector approximation file (Weber
et al., 1998). They index multiple dimensions in a sin-
gle data structure, avoiding the need of scanning the
whole searched dimensional space. However, these
structures have a high up-front creation and mainte-
nance cost, in terms of both computation time and
storage space. Selecting which MDI to create is one
difficult decision that a database administrator (DBA)
must take since the trade-off between the speed-up
of subsequent queries and creation/maintenance costs
must be carefully analyzed (Comer, 1978).
Self-tuning tools (Bruno, 2011) try to alleviate
this problem by automatically selecting the indexes
through a what-if architecture that tricks the query
optimizer into guessing the indexes costs. However,
they only consider uni-dimensional indexes in order
to prune the subset of indexes to be created. They are
also not a good fit for exploratory data analysis where
the workload is unpredictable and where there is no
idle time to invest in a priori index creation.
Adaptive indexing techniques, such as database
cracking (Idreos et al., 2007), attempt to solve the in-
dex selection problem for exploratory data analysis
workloads by presenting an adaptive partial indexing
approach for relational databases. It works by buil-
ding a partial index as a co-product of query proces-
sing. An index is initiated the first time an attribute is
queried, and then continuously refined as subsequent
Holanda, P., Nerone, M., Almeida, E. and Manegold, S.
Cracking KD-Tree: The First Multidimensional Adaptive Indexing (Position Paper).
DOI: 10.5220/0006944203930399
In Proceedings of the 7th International Conference on Data Science, Technology and Applications (DATA 2018), pages 393-399
ISBN: 978-989-758-318-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
393
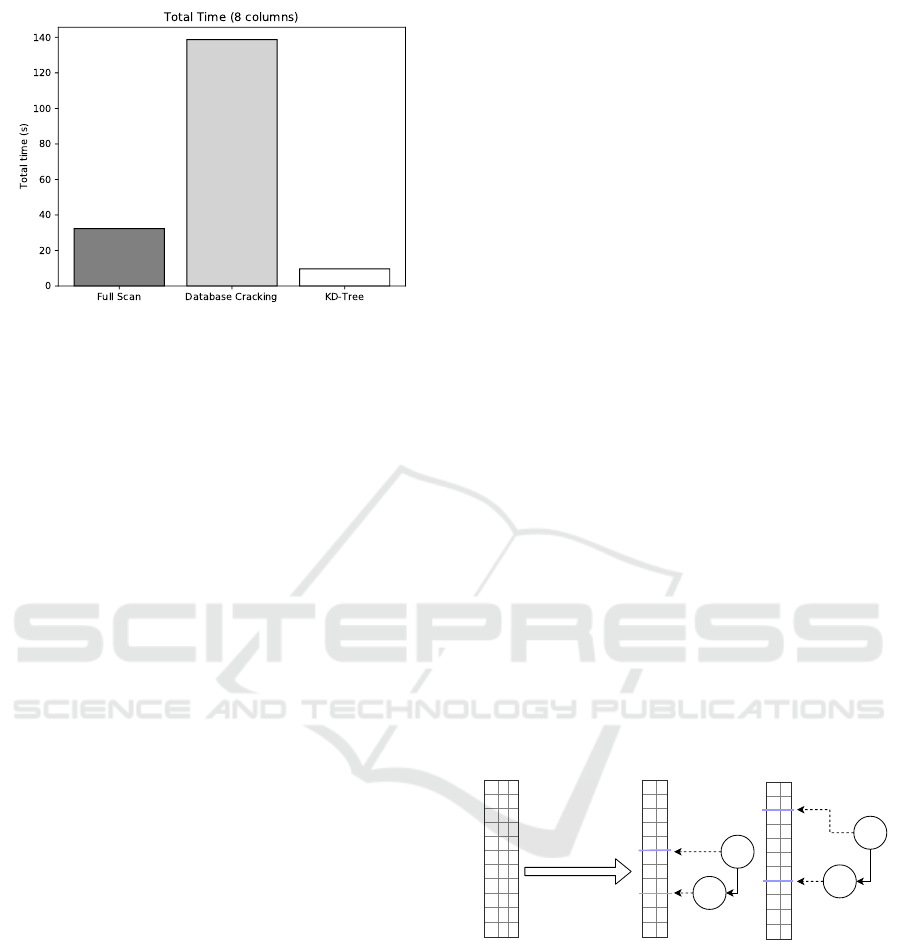
Figure 1: Total Time for multidimensional range queries in
8 Columns.
queries are executed. In this way, the cost of creating
an index is distributed over a stream of queries. Ho-
wever, database cracking and its variations are desig-
ned to generate uni-dimensional indexes, only. Since
each attribute is indexed separately from the others, to
execute an MDRQ it is necessary to look up the indi-
vidual indexes for each dimension and intersect their
results. The latter can be an expensive task, given that
the individual intermediate results can be much larger
than the final result, and because index lookups yield
the matching tuple IDs (or bit-vectors) in different or-
der.
Figure 1 depicts the total cost for a query stream of
1000 MDRQs, with 20% selectivity per attribute, over
an 8-dimensional data set of 10
7
elements. We use
eight instances of database cracking, one per each co-
lumn. The high costs of intersecting the individual in-
termediate results of different columns turn the unidi-
mensional indexing solutions unfit for querying mul-
tidimensional data. Database cracking costs’ surpass
the cost of a full scan and is one order of magnitude
slower than a full multidimensional index.
Covering indexes (Zhang, 2009) or side-ways
cracking (Idreos et al., 2009) avoid the intersection
of per-column intermediate results by keeping all re-
maining dimensions aligned with the leading index
dimension. However, this comes at the expense of
having index-support only for one leading dimension,
while the remaining dimensions need to be scanned.
In case the selectivity per dimension varies strongly
across queries, multiple ”wide” indexes would need
to be built and maintained to suit all queries optimally.
To address these needs we propose a novel appro-
ach for indexing multidimensional data: Multidimen-
sional Adaptive Indexing (MDAI). It works by exten-
ding adaptive indexing in order to produce an MDI as
a side-effect of query processing. In this paper, we
describe our ongoing work on MDAI and present the
Cracking KD-Tree as the first MDAI that generates a
KD-Tree in an adaptive fashion.
Paper Structure. The rest of this paper is structu-
red as follows. Section 2 provides an overview of re-
lated work. Then, Section 3, describes multidimen-
sional adaptive indexing. Section 4 presents a brief
proof of concept and experimental analysis. Finally,
in Section 5, we present our conclusions and discuss
future steps.
2 RELATED WORK
In this section, we present the state of the art on auto-
matic physical database design and MDI structures.
2.1 Automatic Physical Tuning
Self-Tuning Tools (Chaudhuri and Narasayya, 1997;
Agrawal et al., 2000; Valentin et al., 2000) attempt
to solve the index selection problem by automatically
recommending a set of indexes to optimize a known
workload of the system. They work by selecting a
relevant workload, generating a set of indexes that
might be beneficial for it and running them through
the What-If architecture (Chaudhuri and Narasayya,
1998) in order to check if the indexes should be crea-
ted. However, these systems depend on previous wor-
kload knowledge, are only able to create full indexes
and only consider uni-dimensional indexes in order to
prune the index search space. Therefore, they are not
suitable for exploratory systems with MDRQ.
ID X Y
1 4 5
2 3 6
3 2 7
4 1 8
5 0 9
6 9 0
7 8 1
8 7 2
9 6 3
10 5 4
Index on X
ID X
5 0
2 3
3 2
4 1
1 4
10 5
9 6
8 7
7 8
6 9
4
7
ID Y
6 0
7 1
8 2
9 3
10 4
1 5
2 6
3 7
4 8
5 9
1
6
4 <= X < 7 AND
1 <= Y < 6
Index on Y
Figure 2: Database cracking with two dimensional range
query.
Adaptive Indexing (Schuhknecht et al., 2013) is an
alternative to the self-tuning tools. It is especially
useful in scenarios where the workload is unpredic-
table and there is no idle time to invest in index
creation. It tackles these problems by creating in-
dexes that are workload dependent in an incremen-
tal fashion. Figure 2 depicts an example of database
cracking (Idreos et al., 2007) answering a multidi-
mensional range query. The query starts by trigge-
ring the creation of the cracker column (i.e., initially
a copy of column X) where the tuples are clustered
EDDY 2018 - Special Session on Adaptive Data Management meets Self-Adaptive Systems
394
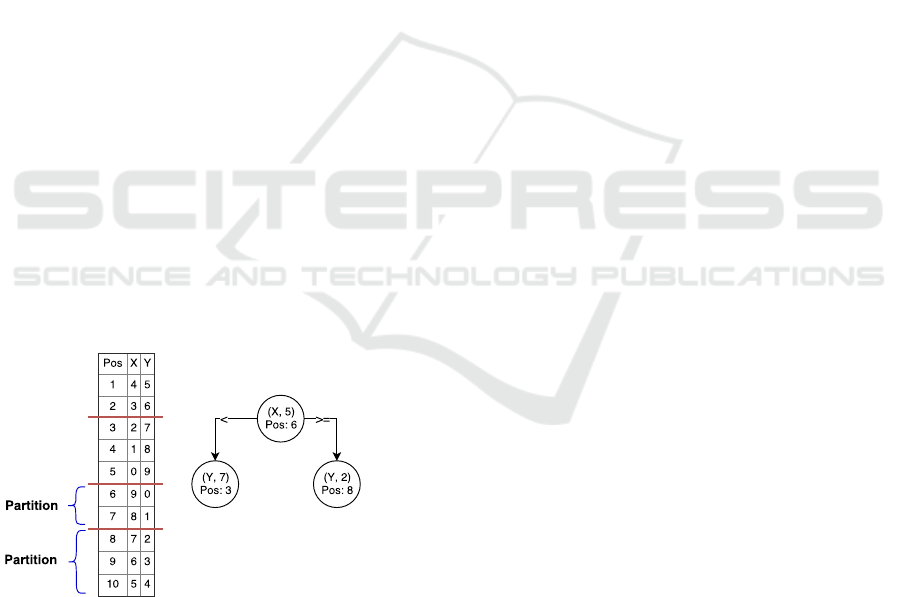
in three pieces reflecting the range predicate on co-
lumn X. The result is then retrieved as a view on the
piece between 4 and 7. Column Y is treated in a simi-
lar way, using predicate boundaries 1 and 6. Finally,
both views need to be intersected by their id column
in order to retrieve the overall result.
Multiple issues with database cracking have been
identified and resulted in different research paths,
such as poor convergence towards a full index (Gra-
efe and Kuno, 2010; Idreos et al., 2011), inefficient
tuple reconstruction (Idreos et al., 2009), unpredicta-
ble performance (Halim et al., 2012), inefficient upda-
tes (Holanda and de Almeida, 2017). More recently a
generic algorithm for adaptive indexing, the adaptive
adaptive indexing (Schuhknecht et al., 2018) was pro-
posed to unify all algorithms in one, where previous
data access paths can be mimicked by setting different
properties.
To the best of our knowledge, all existing adaptive
indexing techniques focus on creating only single-
dimensional indexes, and are thus not suited to effi-
ciently and effectively deal with MDRQs.
2.2 Multidimensional Index Structures
MDI structures can be exploited to accelerate
MDRQs by avoiding the intersection cost necessary
with uni-dimensional indexes and scans. Sprenger et
al. (Sprenger et al., 2018) select three different mul-
tidimensional index structures considered to be the
state-of-the-art for querying multidimensional data.
In the following, we present a brief description of
these three techniques.
Figure 3: KD-Tree indexing two dimensions.
KD-Tree (Bentley, 1975). It is a generalization of
a binary search tree to multidimensional data. Every
node of a KD-Tree holds a key, a discriminator co-
lumn and, at most, two pointers for its children. The
traditional method is using the median of each column
to split the data horizontally. Every level of the tree is
focused in one specific dimension chosen in a round-
robin fashion. Figure 3 depicts a KD-Tree that in-
dexes the dimensions X and Y. The root indexes the
dimension X in its median value 5. The next level in-
dexes the next dimension Y in the medians of the new
pieces defined by X. 7 when X < 5 and 2 otherwise. A
query that requests the ranges X > 5 and 2 < Y < 10
would transverse the tree until reaching node (Y, 2)
and would scan the column partition from position 8
until its end.
R-Tree (Guttman, 1984). Similar to B+-Trees, they
store data in the leaves. However, they use the inner
nodes to hold information in minimum bounding rec-
tangles. Lookup starts at the root and traverses the
tree to the leaves intersecting the query with the mi-
nimum bounding rectangles to determine which sub-
trees may have the searched data, and pruning the re-
maining subtrees.
VA File (Weber et al., 1998). It partitions the
data space into rectangular cells that generate a bit-
encoded approximation of points. Dividing a k di-
mensional space into 2
b
rectangular cells. Where b is
the number of bits used for approximation.
3 MULTIDIMENSIONAL
ADAPTIVE INDEXING
The previous section gave us the necessary motivation
for MDAI. (1) Selecting which MDI to create in an
unpredictable environment is a hard task, (2) a priori
index creation requires idle time that is not available
in exploratory scenarios, (3) although adaptive index-
ing techniques aim to alleviate problems (1) and (2)
they only produce uni-dimensional indexes. Hence,
they are not suited to boost MDRQ.
We propose MDAI as a new technique that brings
adaptivity to multidimensional indexes. MDAI is de-
signed to produce an MDI while taking advantage of
the lightweight adaptive properties from adaptive in-
dexing. We believe that the following modifications
from adaptive indexing must be taken: (1) We group
all columns that are queried with range predicates
together, maintaining the tuple alignment, and copy
them to a table, that we call cracker table, (2) when
swapping elements based on a pivot, we swap the en-
tire row of our cracker table, instead of column ele-
ments and (3) we use an MDI structure to keep track
of the cracker table pieces.
Figure 4 depicts how MDAI works. Consider an
unindexed table, a query Q
1
that queries ranges from
columns C
1
to C
n
, where 1 < n ≤ d, d being the max-
imum number of dimensions of the multidimensional
space. Q
1
triggers the first phase of MDAI, by cre-
ating a cracker table with all the columns aligned by
an explicit id. After the cracker table is created the
Cracking KD-Tree: The First Multidimensional Adaptive Indexing (Position Paper)
395

C
1
Id …C
n
Q
1
:
SELECT *
FROM …
WHERE
L
C1
<C
1
<H
C1
AND … AND
L
Cn
< C
n
< H
Cn
C
1
Id … C
n
L
C1
H
C1
L
…
H
…
L
Cn
H
Cn
Create
C
Tabl e
C
1
…
C
n
Figure 4: Multidimensional Adaptive Indexing.
cracking phase starts. Each range predicate will be
executed sequentially from their order in the query
(i.e., in this case from C
1
to C
n
). At the end of the
cracking phase, we simply need to do a lookup in our
cracking index and retrieve a view, marked in red, that
answers our query.
3.1 Cracking KD-Tree
In this section we describe the Cracking KD-Tree, the
first MDAI algorithm. It implements all the modifica-
tions of an MDAI and produces a KD-Tree as index.
Cracking. The major difference between the
Cracking KD-Tree and a regular KD-Tree is how
they are built. The regular KD-Tree is constructed
based on the medians of each column, whereas the
Cracking KD-Tree is constructed based on incoming
MDRQs. Given an MDRQ, for example x
1
≤ X <
x
2
AND y
1
≤ Y < y
2
, we iterate over the (column,key)
pairs that represent the individual predicate terms,
e.g. (X, x
1
), (X,x
2
), (Y, y
1
), (Y, y
2
), and use them to
successively grow and refine the index. It is impor-
tant to notice that one pair can be inserted in multi-
ple locations and that the levels in the Cracking KD-
Tree are not dimension specific as opposed to the re-
gular KD-Tree. We also implemented a minimal par-
tition size (i.e., L2 cache size) in order to avoid non-
proportionally increased index maintenance overhead
and unnecessary random access that would result
from too many too small partitions.
Lookup. A lookup in the Cracking KD-Tree con-
sists of comparing the current node key with the gi-
ven range. For example, given a key x and a range
x
1
≤ X < x
2
, there are three possible outcomes:
1. x ≤ x
1
: the result of the query is on the right of the
key.
2. x
2
≤ x: the result of the query is on the left of the
key.
3. x ∈ [x
1
, x
2
]:the result of the query is on both sides.
Figure 5 depicts a bi-dimensional example of the
Cracking KD-Tree. In this example, Figure 5(a) re-
presents the uncracked cracker table. Query Q
1
starts
by triggering the first cracking iteration on column X
using its lower predicate boundary 4. After swap-
ping the elements of X around 4 the Cracking KD-
Tree root node is inserted. It holds the information
regarding the cracked column, the pivot value and the
table position, depicted in Figure 5(b). The second
cracking iteration is then started and we continue to
crack the column X. However, we now crack it using
its upper predicate boundary 7, creating a child node
to the root, depicted in Figure 2(c). Finally, the last
cracking iteration starts, now on column Y. Since the
root node and its child do not give us any informa-
tion about Y we must follow all possible paths, and
crack Y on 1 in all existing pieces, resulting in Fi-
gure 5(d). After the cracking phase is finished, we
perform a lookup operation at the index. Starting
from the root of the tree, we can see that its key 4
is equal to the inclusive lower predicate boundary of
4 ≤ R.X < 7. This means that need to descend to the
right child of the root node. There, we see that its key
7 is equal to the exclusive upper predicate boundary of
4 ≤ R.X < 6, which leads us to its left child. Finally,
the leaf with key 1 is equal to the inclusive lower pre-
dicate boundary of 1 ≤ R.Y . Hence, we can return the
tuples in positions 6 and 7 of the cracker table, shaded
in red in Figure 5(d), as the query answer.
4 EXPERIMENTS
In this section, we present a brief experimental ana-
lysis to demonstrate the strong potential benefits of
MDAI.
Setup. We implemented the Cracking KD-Tree in a
single-threaded stand-alone program written in C++
and compiled with GNU g++ version 7.3.1 using op-
timization level -O3. All experiments were conducted
on a machine equipped with 256 GB of main memory
and two 2.6 GHz Intel Xeon E5-2650 v2 CPUs, each
with 20 MB L3 cache, 8 cores and hyper-threading
enabled, running Fedora 26.
1 SELECT COUNT(R.C1)
2 FROM R
3 WHERE LowC1 < R.C1 < HighC1 AND ...
4 AND LowCn < R.Cn < HighCn
Listing 1: Query form used on experiments.
Our data set consists of a table with 8 8-byte inte-
ger attributes holding 10
7
tuples. The values per attri-
bute are independently uniformly distributed.
All queries are of the form depicted in Listing 1.
EDDY 2018 - Special Session on Adaptive Data Management meets Self-Adaptive Systems
396
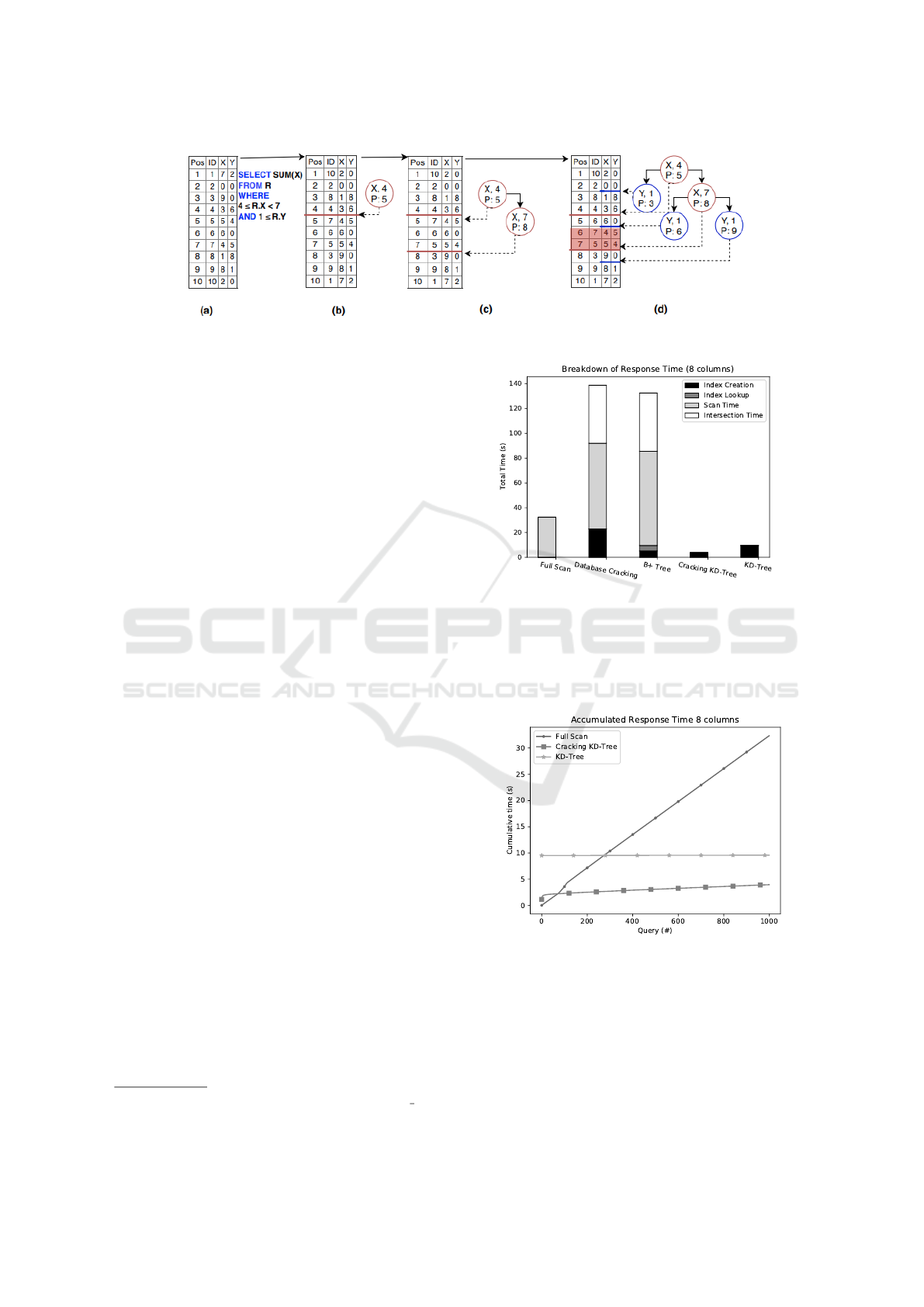
Figure 5: Cracking KD-Tree.
Where n is the number of dimensions queried. All the
queries have selectivity equal to 0.2 per column, one
might notice that the total selectivity of the queries in
the query stream will vary since the query predicates
are selected in a random pattern. We repeat the entire
workload 10 times and take the average runtime of
each query as the reported time.
We implemented four different algorithms to com-
pare with our Cracking KD-Tree.
Full Scan. We use a vectorized, predicated scan ap-
proach (Boncz et al., 2005) that produces a candidate
list per scanned vector of a column. The vector size is
in accordance to the L2 cache size.
Standard Cracking AVL. Each column goes through
the process of database cracking separately. After-
wards, the results are intersected by the creation of
bit-vectors
1
.
Full Index B+ Tree. Each column is indexed using
a B+ Tree created before running the workload. To
answer the queries, we do a lookup in each column
and intersect the results with bit-vectors.
Full Index KD-Tree. All columns are indexed using
a KD-Tree pivoting by median values and choosing
the dimensions in a round robin fashion. In order
to find the medians, we use a quick-sort variant that
instead of ordering a column, stops execution when
finding its median value. The query result is then gi-
ven by a lookup in the KD-Tree.
Figure 6 depict the breakdown of accumulated re-
sponse time for all algorithms. We can see that both
uni-dimensional indexes have a similar cost, around
140 seconds in total, mainly due to the time spent
in scanning, creating and intersecting the interme-
diate results with the bit-vectors. The full scan is
four times cheaper than building, traversing and in-
tersecting multiple uni-dimensional indexes to answer
the query. The KD-Tree achieves a three times better
response time than the full scan, with index creation
being its highest cost. This issue is mitigated by the
Cracking KD-Tree that efficiently spreads it throug-
1
We use the standard c++ library: boost::dynamic bitset
to generate the bit-vectors
Figure 6: Total response time breakdown of workload with
8 columns.
hout the query stream. However, the index creation
cost still takes a considerable chunk of time on the
Cracking KD-Tree mainly due to the relaxation of the
one dimension per level restriction of the KD-Tree.
Figure 7: Cumulative response time for 8 columns.
Figure 7 depict the cumulative response time for
the full scan and both KD-Trees. The full scan has a
linear cost, presenting about the same cost for every
scan. The Full KD-Tree has the highest initial cost
due to its a priori creation, costing two orders of
magnitude more than a full scan, but all subsequent
queries have low additional costs, taking around 280
queries for this initial investment to pay off. The
Cracking KD-Tree: The First Multidimensional Adaptive Indexing (Position Paper)
397
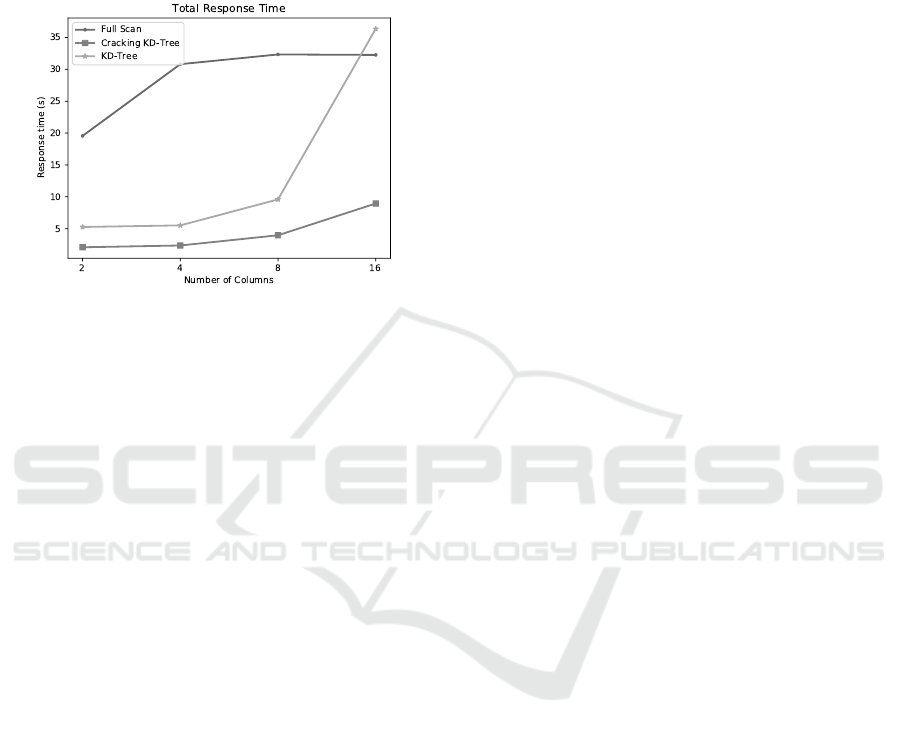
Cracking KD-Tree’s first query cost is one order of
magnitude higher than a full scan, and it quickly con-
verges towards a full index speed, presenting a lower
response time than a full scan around query 7, and
only needing 70 queries for its creation investment to
pay off.
Figure 8: Total time for multiple columns.
Figure 8 depicts the total time for running our
query stream under a different number of dimensi-
ons. Since we maintain the same selectivity per co-
lumn (i.e., 0,2%), for 16 columns our query results
are all empty. We can see that the full scan increa-
ses its total time dependent on the intermediate result
size due to the use of candidate lists. Since the overall
selectivity of the queries decreases when we increase
the number of dimensions the full scan can maintain
good scalability after four dimensions. The Full KD-
Tree depends mostly on time spent creating the index,
so its cost grows exponentially when we increase the
number of columns. The Cracking KD-Tree presents
better scalability when compared to a Full KD-tree
due to its lazy nature.
5 CONCLUSION & FUTURE
WORK
MDAI introduces new aspects that were unexplored
by adaptive indexing and that require further investi-
gation. We describe the following as the aspects that
shall be explored as our next steps in this research:
• Related Work Optimizations. In our proof-of-
concept, we always use one uni-dimensional in-
dex per column and later intersect their interme-
diate results using bit-vectors. However, we can
also use a covering index which might be more
competitive than the current approach. Anot-
her possibility would be to map the n-dimensions
to one dimension by using Z-Ordering (Ramsak
et al., 2000) and indexing it.
• Cracking KD-Tree. The Cracking KD-Tree pre-
sented in this work produces multiple dimensions
in the same level by constructing it using the order
of range predicates presented in the query. Other
design choices can be made, as ignoring parts of
the predicates to preserve the dimensions per le-
vel, or completely ignoring the query predicates
and select the pivot points by calculating the me-
dians, one for each predicate.
• Adapting other MDI. Other data structures are
also good candidates to MDAI when increasing
the number of dimensions. For instance, Vantage-
point Tree, Ball-trees and M-Tree (Liu et al.,
2006), and Locality Sensitive Hashing (Andoni,
2009) present similar searching properties to KD-
Trees, although their structure demand heavier
storage space compared to the KD-Tree increa-
sing the runtime for maintenance.
• Benchmarks: Our experimental evaluation is li-
mited by only using uniformly random distributi-
ons for the data and a fixed selectivity for the que-
ries. Other distributions and selectivities must be
explored. Real-world multidimensional data and
workloads should also be tested (e.g., the genomic
multidimensional range query benchmark (Spren-
ger et al., 2018)).
• Machine Learning. In-database Machine Lear-
ning is a trend and KD-Trees are broadly used for
approximate nearest neighbor (k-NN) search: gi-
ven a labeled object, find the most similar labe-
led object. Applications of the k-NN search, in-
clude, text categorization, searching image data-
bases, finding duplicate records. Our agenda in-
cludes studying the impact of our Cracking KD-
Tree to save search time at little cost in quality of
the nearest neighbor in some of these applications.
ACKNOWLEDGMENTS
This work was funded by the Netherlands Organi-
sation for Scientific Research (NWO), project “Data
Mining on High-Volume Simulation Output” (Ho-
landa) and by CAPES Brazil.
REFERENCES
Agrawal, S., Chaudhuri, S., and Narasayya, V. R. (2000).
Automated Selection of Materialized Views and In-
dexes in SQL Databases. In VLDB, pages 496–505.
EDDY 2018 - Special Session on Adaptive Data Management meets Self-Adaptive Systems
398

Alvanaki, F., Goncalves, R., Ivanova, M., Kersten, M., and
Kyzirakos, K. (2015). Gis navigation boosted by co-
lumn stores. PVLDB, 8(12):1956–1959.
Andoni, A. (2009). NN search : the old, the new, and
the impossible. PhD thesis, Massachusetts Institute
of Technology, Cambridge, MA, USA.
Bentley, J. L. (1975). Multidimensional binary search trees
used for associative searching. Communications of the
ACM, 18(9):509–517.
Boncz, P. A., Zukowski, M., and Nes, N. (2005). Monetd-
b/x100: Hyper-pipelining query execution. In CIDR,
volume 5, pages 225–237.
Bruno, N. (2011). Automated Physical Database Design
and Tunning. CRC-Press.
Chaudhuri, S. and Narasayya, V. (1998). AutoAdmin
“What-if” Index Analysis Utility. SIGMOD Record,
27(2):367–378.
Chaudhuri, S. and Narasayya, V. R. (1997). An Efficient,
Cost-Driven Index Selection Tool for Microsoft SQL
Server. In VLDB, volume 97, pages 146–155.
Comer, D. (1978). The Difficulty of Optimum Index Se-
lection. TODS, 3(4):440–445.
Graefe, G. and Kuno, H. (2010). Self-selecting, self-tuning,
incrementally optimized indexes. In EDBT, pages
371–381. ACM.
Guttman, A. (1984). R-trees: A dynamic index structure for
spatial searching. In SIGMOD, pages 47–57.
Halim, F., Idreos, S., Karras, P., and Yap, R. H. (2012). Sto-
chastic Database Cracking: Towards Robust Adaptive
Indexing in Main-Memory Column-Stores. VLDB,
5(6):502–513.
Ho, C.-T., Agrawal, R., Megiddo, N., and Srikant, R.
(1997). Range queries in OLAP data cubes. In SIG-
MOD, volume 26, pages 73–88.
Holanda, P. and de Almeida, E. C. (2017). SPST-Index: A
Self-Pruning Splay Tree Index for Caching Database
Cracking. In EDBT, pages 458–461.
Idreos, S., Kersten, M. L., and Manegold, S. (2009). Self-
organizing Tuple Reconstruction in Column-stores.
SIGMOD, pages 297–308.
Idreos, S., Kersten, M. L., Manegold, S., et al. (2007). Da-
tabase Cracking. In CIDR, volume 3, pages 1–8.
Idreos, S., Manegold, S., Kuno, H., and Graefe, G. (2011).
Merging What’s Cracked, Cracking What’s Merged:
Adaptive Indexing in Main-Memory Column-Stores.
VLDB, 4(9):586–597.
Li, H. (2011). Tabix: fast retrieval of sequence featu-
res from generic tab-delimited files. Bioinformatics,
27(5):718–719.
Li, X., Kim, Y. J., Govindan, R., and Hong, W. (2003).
Multi-dimensional range queries in sensor networks.
In SenSys, pages 63–75.
Liu, T., Moore, A. W., and Gray, A. G. (2006). New algo-
rithms for efficient high-dimensional nonparametric
classification. Journal of Machine Learning Research,
7:1135–1158.
Poess, M. and Stephens, Jr., J. M. (2004). Generating thou-
sand benchmark queries in seconds. In VLDB, pages
1045–1053.
Ramsak, F., Markl, V., Fenk, R., Zirkel, M., Elhardt, K.,
and Bayer, R. (2000). Integrating the ub-tree into a
database system kernel. In VLDB, volume 2000, pages
263–272.
Schuhknecht, F. M., Dittrich, J., and Linden, L. (2018).
Adaptive adaptive indexing. ICDE.
Schuhknecht, F. M., Jindal, A., and Dittrich, J. (2013).
The Uncracked Pieces in Database Cracking. PVLDB,
7(2):97–108.
Sprenger, S., Sch
¨
afer, P., and Leser, U. (2018). Multidi-
mensional range queries on modern hardware. arXiv
preprint arXiv:1801.03644.
Valentin, G., Zuliani, M., Zilio, D. C., Lohman, G., and
Skelley, A. (2000). DB2 Advisor: An Optimizer
Smart Enough to Recommend Its Own Indexes. In
ICDE, pages 101–110.
Weber, R., Schek, H.-J., and Blott, S. (1998). A quantitative
analysis and performance study for similarity-search
methods in high-dimensional spaces. In VLDB, vo-
lume 98, pages 194–205.
Zhang, D. (2009). Covering index. In Liu, L. and
¨
Ozsu,
M. T., editors, Encyclopedia of Database Systems, pa-
ges 516–517. Springer US.
Cracking KD-Tree: The First Multidimensional Adaptive Indexing (Position Paper)
399
