
A Cyclical Model for Waste Products Inventory-Routing
at Power Stations
Yiqing Zhong, Guopeng Yao, Yangyang Sun, Yang Li and Xian Zhou
State Key Laboratory of Coal-Based Clean Energy, Huaneng Clean Energy Research Institute, Beijing, China
{Zhongyiqing, Yaoguopeng, Sunyangyang, Liyang, Zhouxian}@hnceri.com
Keywords: Inventory-routing, Mixed-integer program, Optimization, Waste Product.
Abstract: The inventory routing problem (IRP) is one of the challenging optimization problems in supply chain
management (SCM). Inventory Routing Problems currently get a lot of attention, in which a typical property
is that inventory control and vehicle routing tasks are taken into account simultaneously. The objective of the
IRP is to jointly determine optimal quantities of the product to be delivered to the customers, delivery times
and optimal vehicle routes for the shipment of these quantities. At power enterprises, SCM strategies are
more and more interesting for the resource optimization. In this paper, a cyclical inventory routing problem is
modeled and accounted for one distribution system of waste products at the power stations. This proposed
problem is formulated as a linear mixed-integer program, in which the demand rates of customers are
assumed to be constant. As to the resource optimization, a practical instance is presented and thoroughly
discussed, to illustrate the behavior of the proposed model.
1 INTRODUCTION
Waste Products at power stations, e.g. coal fly ash,
plaster etc., are comprehensively utilized in building
industry. However a challenging problem when ones
intend to deliver and store such waste products, e.g.
coal fly ash, due to the fact that it is dispersive
mixed-solid and is scattered very easily,. As a result,
special vehicles (i.e. tank trucks) have to be
employed for its delivery, and high costs arise.
In this paper, a cyclical multi-period inventory
routing problem (IRP) is discussed, in which the
delivery and storage of coal fly ash can be
represented. Inventory routing problems involve the
integration of inventory management and vehicle
routing optimization. The typical main objective in
such problems is to determine an optimal
distribution policy, consisting of a set of vehicle
routes and delivery quantities that minimize the total
inventory holding and transportation costs. The IRP
arises in distribution systems implementing a
'Vendor Managed Inventory' (VMI) policy.
Compared with the traditional non-integrated
inventory replenishment and vehicle scheduling, in
which customers manage their inventories
themselves and call in their orders, overall inventory
and routing performances throughout the supply
chain are by far superior when VMI is implemented.
Nowdays, the IRP has been one of the most
challenging and interesting optimization problems in
supply chain and logistics management.
2 A BRIEF LITERATURE
REVIEW
Since Bell et al. (1983) first investigated the
integrated inventory management and vehicle
scheduling, various versions of the inventory routing
problems have been extensively studied. A large
variety of solution approaches have also been
proposed for the solution of these problems.
Inventory routing problems can be modeled and
approached in different ways depending on the
characteristics of its parameters. Different models
can be obtained for example, when customers
consume the product at a stable or at a variable rate;
when the planning horizon is finite or infinite, and
so on. Dror and Ball (1987) decompose a multi-
period IRP into series of single period problem.
They study the problem with constant demands and
then propose and compare two solution approaches
for the resulting single period problem. Campbell et
al. (2002) and Campbell and Savelsbergh (2004)
also worked on the multi-period IRPs where the
decisions are executed over a finite horizon. For
recent research devoted to the multi-period IRPs, we
refer to e.g. Yu et al. (2008), Taarit et al. (2010), etc.
46
Zhong, Y., Yao, G., Sun, Y., Li, Y. and Zhou, X.
A Cyclical Model for Waste Products Inventory-Routing at Power Stations.
In 3rd International Conference on Electromechanical Control Technology and Transportation (ICECTT 2018), pages 46-50
ISBN: 978-989-758-312-4
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Other fundamental contributions in the class of
infinite inventory routing problems are for example
Anily and Federgruen (1990) and Hall (1992).
Aghezzaf et al. (2006) address a special case of
infinite inventory routing problems, namely, the
cyclic inventory routing problem (CIRP), in which a
single distribution center, supplying a single
product, serves a set of customers, each being visited
by an assigned vehicle in a cyclical manner and in
such a way that at no moment a stock-out should
occur at any of the customers. Later this cyclic
problem and its variants are further discussed in e.g.
Raa and Aghezzaf (2009) and Zhong and Aghezzaf
(2011).
The strategy presented in inventory routing
problems allows to reduce costs if a supplier or a
third-party logistics server regards the delivery and
storage of coal fly ash as a model of the IRP, due to
the fact that the supplier or the logistics provider
may coordinate both inventory control and
transportation policy. More specially, a multi-period
inventory routing problem (MP-IRP) is concerned
with a distribution system using a fleet of
homogeneous vehicles to distribute the product from
a single depot to a set of customers having stable
demands. The considered distribution policies are
executed over a given finite horizon, for example on
a set T of consecutive periods (or days). The
objective is to determine the quantities to be
delivered to the customers, the delivery time, and to
design the vehicle delivery routes, so that the total
distribution and inventory costs are minimized. The
resulting distribution plan must prevent stockouts
from occurring at all customers during the planning
horizon. A mixed-integer model is built up for this
MP-IRP, in which the distribution pattern of 'multi-
tour' is employed, i.e. a vehicle can make a set of
different tours when it is used (see e.g. Aghezzaf et
al. 2006, Zhong and Aghezzaf (2011). In addition,
the presented model considers the vehicle fleet size
as part of the optimization problem and has to be
determined. Also, the initial inventory levels at the
customers have to be determined in this model,
instead of predefined amounts as done in other
similar works (see for example Taarit et al. 2010 and
references therein).
The remainder of this paper is organized as
follows. In Section 3, a linear mixed-integer
formulation for the MP-IRP is presented. In Section
4, a practical case is studied to illustrate the behavior
of the presented model. Finally, some concluding
remarks are provided in Section 5.
3 PROBLEM FORMULATION
To be more precise, the discussed multi-period IRP
consists of a single distribution center r using a fleet
of homogeneous trucks to distribute a single product
to a set of geographically dispersed customers S over
a given planning horizon. It is assumed that
customer-demand rates and travel times are stable
over time. Thus, the objective of this MP-IRP is to
determine the quantities to be delivered to the
customers, the delivery time, and to design the
vehicle delivery routes, so that the total distribution
and inventory costs is minimized while preventing
stockouts from occurring at all customers during the
whole planning horizon.
To build up this mixed-integer model for the
MP-IRP, some main assumptions are made below:
1) The time necessary for loading and unloading
a truck is neglected in the model;
2) Inventory capacities at the depot are assumed
to be large enough so that the corresponding
capacity constraints can be omitted in the model;
3) Transportation costs are assumed to be
proportional to travel times;
4) Split delivery is not allowed, such that a
customer is always replenished by one vehicle, in
the same tour in each period of the planning horizon.
A more formal description and a proposed linear
mixed-integer formulation of the MP-IRP are given
in the following paragraphs:
Let H={1,2,...,T} be the planning horizon set of
consecutive periods indexed by t. Let
be the size
in time unit of one period,, for example 8 working
hours. Let S be the set of customers indexed by i and
j and S
+
= S U {0} where 0 represents the depot. A
homogeneous fleet of trucks V is used to serve these
customers. The other necessary parameters of the
model are given below:
v
: the fixed operating cost of truck
Vv
(in
RMB per truck);
v
: the capacity of truck
Vv
(in ton);
jt
: the holding cost of per unit per period of
product at customer
Sj
(in RMB per ton per
period);
0j
: the initial holding cost of per unit of
product at customer
Sj
(in RMB per ton);
jt
D
: the demand at customer
Sj
in period
Ht
(in ton), i.e.
jtjt
dD
for
Ht
, where
A Cyclical Model for Waste Products Inventory-Routing at Power Stations
47

jt
d
represents the demand rate at customer j (in ton
per hour);
: travel cost of truck (in RMB per km per
hour);
: truck speed (in km per hour);
ij
tr
: duration of a trip from customer
Si
to
customer
Sj
(in hour);
j
C
: the inventory capacity at customer j (in ton).
The variables of the model are defined as
follows:
jt
I
: the inventory level of customer
Sj
at
the end of period
Ht
(in ton);
0j
I
: the initial inventory level of customer
Sj
(in ton);
v
ijt
Q
: the quantity of product remaining in truck
Vv
when it travels directly to the customer
Sj
from customer
Si
in period
Ht
.
This quantity equals zero when the trip (i, j) is not
on any tour made by truck
Vv
in period t (in
ton);
jt
q
: the quantity that is delivered to customer
Sj
in period
Ht
, and 0 otherwise (in ton);
v
ijt
x
: a binary variable sets to 1 if customer
Sj
is visited immediately after customer
Si
by truck
Vv
in period
Ht
, and 0
otherwise;
v
y : a binary variable sets to 1 if truck
Vv
is
being used, and 0 otherwise;
Thus, the linear mixed-integer formulation for
the multi-period IRP is presented as follows:
)1(
00
TtSjSj
jjjtjt
VvVvTt
SiSj
v
ijtijvv
II
xtryCV
Subject to:
)2(,1 TtSjx
Vv
Si
v
ijt
)3(,,0 VvTtSjxx
SiSk
v
jkt
v
ijt
)4(
1101
SjDqII
jjjj
)5(2,,
1,
tTtSjDqII
jtjttjjt
)6(, TtSjqQQ
Vv
Si
Vv
Sk
jt
v
jkt
v
ijt
)7(,,, VvTtSjixQ
v
ijt
vv
ijt
)8(, VvTtxtr
v
ijt
SiSj
ij
)9(,,
0
SjTtTtII
jtj
)10(,, VvTtSjyx
Si
vv
ijt
)11(,,,
0,0,,0},1,0{,
0
VvTtSji
qQCIIyx
jt
v
ijtjjtj
vv
ijt
Three cost components are taken into account in
the model: the total fixed operating cost of using the
truck(s); the total transportation cost; the total
inventory holding cost, including the initial
inventory holding cost and the inventory holding
cost at every end of period
Ht
. For the
restrictions, constraints (2) guarantee that each
customer is visited by each truck at most once in
period t. Constraints (3) are the usual flow
conservation constraints assuring that if a truck
arrives at a customer, it must leave after it served
this customer to a next customer or to the depot.
Constraints (4), (5) are the inventory balance
constraints of each customer. Constraints (6) are the
delivered load balance constraints. These constraints
eliminate possible formation of sub-tours.
Constraints (7) ensure that the quantity carried by a
vehicle should not exceed the truck's maximum
capacity. Constraints (8) indicate that the total travel
time of a vehicle should not exceed the considered
horizon length in each period. Constraints (9)
indicate that the initial inventory level at customer j
at the end of period T shall cover its initial inventory.
Constraints (10) indicate that at every period, a
vehicle cannot be used to serve any customer unless
this vehicle is already selected. Constraints (11) are
the integrality and sign constraints to be imposed on
the variables, in which the capacity constraints at all
customers are taken into account.
4 CASE STUDY
To gain a better understanding of the MP-IRP's
model, this section provides a small practice
example to illustrate different behaviors of the MP-
IRP's model, in which variable initial inventories are
taken into account. This example corresponds to a
third-party logistics company delivers the coal fly
ash from one power station to a set of 7 customers,
ICECTT 2018 - 3rd International Conference on Electromechanical Control Technology and Transportation
48
including 5 cement plants and 2 brickyards. To be
more precise, let us consider this small instance for
the MP-IRP, consisting of 7 customers indexed by
{1, 2
,
..., 7}, and a single depot (i.e. the power plant)
indexed by 0. These 7 clients are distributed
uniformly over a square of 100 by 100 km. A fleet
of homogeneous trucks with capacity 35 ton is
available for the distribution of the product. The
fixed using cost of the truck
is 800RMB per day.
The truck's average speed
is 50 km per hour, and
the travel cost
is 8RMB per km. In this case the
planning horizon set contains 3 consecutive periods
(i.e. 3 days), and the size of one period
is assumed
to be 8 hours. Demands of these clients and the
inventory holding costs for each client are shown in
Table 1 below.
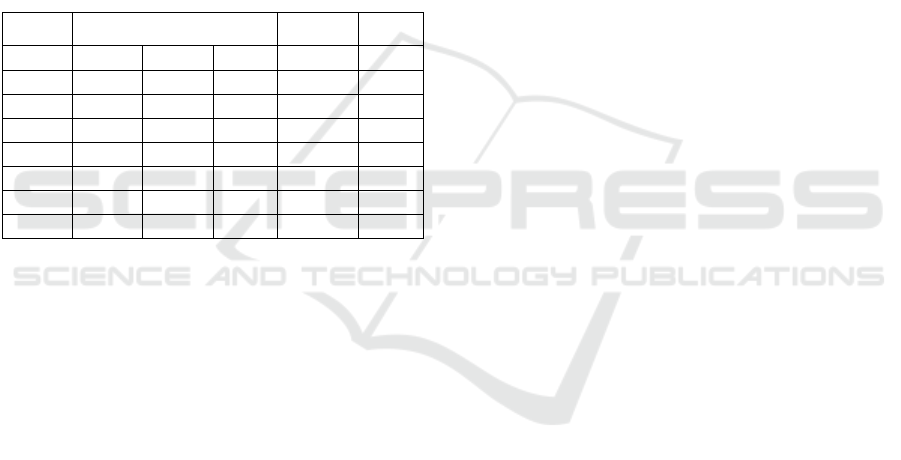
Table 1 Parameters for a case of 7-clients
D
jt
(t)
j
(R/t)
d
j
(t/h)
Client t=1 t=2 t=3
1 8.07 9.27 9.57 0.32 2.99
2 3.93 4.53 3.33 1.28 1.31
3 7.05 7.65 8.70 1.18 2.60
4 6.54 5.28 5.91 1.17 1.97
5 5.61 5.85 6.09 0.41 1.95
6 6.27 5.97 6.57 0.70 2.09
7 9.42 8.28 9.06 0.86 2.94
By solving the instance, the optimal solution
shows that a fleet of 2 trucks is required to replenish
the customers. The delivery routes in each period are
shown below, with the total cost around 9195RMB
(for 3 days).
A. t=1: Vehicle 1 :={(3), (7)}; Vehicle 2:={(2, 4,
5)}.
B. t=2: Vehicle 1 :={(4, 6)};Vehicle 2:={(1)}.
C. t=3: no delivery occurs.
Due to the fact that variable initial inventory
arises in the model, it is allowed the solver to find a
best three-way tradeoff for each customer, among
the initial inventory, the inventory at the end of
every period and the quantity to be delivered to
each, such that the total distribution and inventory
costs can be reduced as much as possible. According
to the financial statistics of the company, without the
logistics optimization presented above, the average
running cost is around $5000$RMB per day in this
case, where the operation manner corresponds to
that the company receives the orders given by the
customers, the trucks are sent and the deliveries
occur then. As a result, one can observe that the MP-
IRP model for this coal fly ash distribution system
might achieve a cost saving around 38.7% when this
optimization model is used.
5 CONCLUSION
This paper provides a specific multi-period
inventory routing problem (MP-IRP) that might be
addressed for the distribution of coal fly ash. In
general, it consists in a single depot distributing a
single product to a set of customers having
stationary demands, using a fleet of homogeneous
vehicles over a given finite horizon. The objective is
to determine the quantities to be delivered to the
customers, the delivery time, and to design the
vehicle delivery routes, so that the total distribution
and inventory costs are minimized. The presented
MP-IRP is formulated as a linear mixed-integer
program with some side constraints. A practical case
is studied to illustrate the behaviors of the MP-IRP
and the merits of such a model. The extensions to
this problem, if for example, the variants by taking
stochastic inventory into account or some efficient
meta-heuristics for the model, are worthy being
investigated further.
ACKNOWLEDGEMENTS
This paper is supported by the Foundation for
Science and Technology of China Huaneng Group
(HNKJ16-H02).
REFERENCES
Bell, W. J., Dalberto, L.M., et al., 1983.Improving the
distribution of industrial gases with an on-line
computerized routing and scheduling optimizer.
Interfaces, Vol.13, No.6, pp. 4-23.
Dror M. and Ball M., 1987. Inventory-routing: Reduction
from an Annual toa Short Period Problem. Naval
Research Logistics Quarterly, 34, pp.891-905.
Campbell, A.M., et al., 2002. Inventory Routing in
Practice. Society for Industrial and Applied
Mathematics, Philadelphia, pp. 309-330.
Campbell A.M. and Savelsbergh M., 2004. A
decomposition approach for the inventory routing
problem. Transportation Science, Vol.38, No.4,
pp.488-502.
Yu Y., Chen H.X et al., 2008. A new model and hybrid
approach for large scale inventory routing problem.
European Journal of Operational Research, 189, pp.
1022-1040.
A Cyclical Model for Waste Products Inventory-Routing at Power Stations
49

Taarit N.B, et al., 2010. A lagangian heuristic method and
an iterative approach for the inventory routing
problem. MOSIM’10, Hammamet, Tunisia.
Anily S. and Federgruen A., 1990. One-warehouse
Multiple Retailer Systems with Vehicle Routing Costs.
Management Science, 36, pp. 92-114.
Hall R.W., 1992. A Note on Bounds for Direct Shipping
Costs. Management Science, 38, pp. 1212-1214.
Aghezzaf E.H., et al., 2006. Modeling Inventory Routing
Problem in Supply Chain of High Consumption
Products. European Journal of Operation Research,
169, pp. 1048-1063.
Raa B. and Aghezzaf E.H., 2009. A Practical Solution
Approach for the Cyclic Inventory Routing Problem.
European Journal of Operational Research, Vol. 192,
No.2, pp.429-441.
Zhong Y.Q. and Aghezzaf E.H., 2011. Combining DC-
programming and Steepest-Descent to Solve the
Single-Vehicle Inventory Routing Problem. Computer
& Industrial Engineering, Vol.61, No.2, pp. 313-321.
ICECTT 2018 - 3rd International Conference on Electromechanical Control Technology and Transportation
50
