The Adaptive Control of Aircraft Brake Based on Asymmetric

Barrier Lyapunov Function

Jiuli Lu, Zhaohui Yuan and Bo Liang

School of Automation, Northwestern Polytechnical University, 710129, Xi’an, Shaanxi, China

lu

j

iulilove

@

163.com

Keywords: Anti-skid Brake, Asymmetric, Slip Rate Constraint, Brake Efficiency.

Abstract: Considering the complexity, non-linearity and uncertainty of aircraft antiskid control system, the author

takes such shortcomings of traditional “PD + PBM” control methods into account as low braking efficiency

and deep skidding on hybrid runways, and puts forward the constraint control algorithm of slip rate based

on asymmetric barrier Lyapunov function, which meets the purpose of adaptive full-regulation from the

concept of system integration that the slip ratio is also satisfied in the stable region where it is constrained,

so as to improve the braking efficiency. By comparing with the simulation results of the traditional “PD +

PBM” control algorithm, the author tries to show that the braking process has a good follow-up performance

and a smooth brake curve, which avoids the problem of low-speed skidding, optimizes the braking

performance and improves braking efficiency based on adaptive control algorithm of slip rate constraint.

1 INTRODUCTION

Aircraft anti-skid braking system is a complex non-

linear and uncertain system, which is affected by

many uncertainties during the landing brake process

of aircraft. It makes the structural parameters have

time-varying characteristics. Therefore, it is the key

and difficulty in the field of aircraft brakes how to

ensure the superiority of braking performance

through system design. However, the design of

system control algorithm is the key factor affecting

the braking performance of the system and the most

important factor in system design. At present, the

conventional “PID with pressure offset” control is

mostly used in practical engineering in China, that is,

the “PD + PBM” control method. Although the

system has some intelligence through the PBM

pressure bias design and the performance of the dry

runway is good, the system still has the problems of

low speed slippage and poor adaptability to the wet

runway. In the AC NO.25-7A, this method was

identified as “quasi-regulation” mode, and wet

runway braking efficiency was only identified as

50%. While such overseas professional

manufacturers are now using adaptive “full

regulation” control method as Goodrich, Safran and

Meggitt. “Full regulation” control mode was

identified as the braking efficiency of 80%, which

can meet the requirements for braking performance.

Some research has been made on adaptive

control theory of aircraft braking system at home

and abroad, mainly including feedback linearization

theory (

TANELLI M, ASTOLFI A, SAVARESI S M,

2008

), fuzzy control (R.Babuska, H.B.Verbruggen,

1996), iterative learning (MI C T, LIN H, ZHANG Y,

2005

), robust control (BASLAMISLI S C，K SE I E,

ANLAS G,2007

), synovial control (TANELLI M,

FERRARA A, 2013; CHO D-W, CHOI S, 1999; CHOI S,

CHO D-W, 2001; HEBDEN R G, EDWARDS C,

SPURGEON S K, 2004

), model- control (Shi Wei, Liu

Wensheng, Chen Jianqun, 2012

), etc. But the

confidentiality and competition is taken into account,

the relevant literature abroad only involves a brief

description of the principle for its aircraft brake

control, without the specific control algorithm in

detail. However, most domestic methods are devoted

to obtaining better control performance by adjusting

the expected value of slip ratio. Direct consideration

is rarely given to the working state of the aircraft

anti-skid braking system and its impact on the entire

aircraft system.

Based on this, the author presents a slip-rate-

adaptive control based on asymmetric barrier

Lyapunov function. The adaptive control law is

designed based on the stability of the constrained

slip ratio. On the one hand, the system works in a

stable area from the system integration level; on the

102

Lu, J., Yuan, Z. and Liang, B.

The Adaptive Control of Aircraft Brake Based on Asymmetric Barrier Lyapunov Function.

In 3rd International Conference on Electromechanical Control Technology and Transportation (ICECTT 2018), pages 102-109

ISBN: 978-989-758-312-4

other hand, it achieves the purpose of adaptive full-

regulation, thus improves braking efficiency.

2 NONLINEAR MATHEMATICAL

MODEL OF AIRCRAFT ANTI-

SKID BRAKING SYSTEM

2.1 Aircraft ground friction model and

dynamic model

The brake control needs to establish a simplified

mathematical model on the basis of reasonable

assumptions (Wang Jisen, 2001; Qiu Yanan,

2016).Taking aerodynamic characteristics into

account, the equilibrium equations in the

longitudinal, vertical and pitch directions are:

⎪

⎩

⎪

⎨

⎧

+=+−

=−−−

=−−+

hnfanNhVKTbN

NnNFG

mVnfFVKT

tXV

y

XXXV

1102

21

10

)(

0

(1)

In which,

2

5.0

XXX

SVCF

ρ

=

,

2

5.0

Xyy

SVCF

ρ

=

,

11

Nf

μ

=

Assuming that the landing gear is a rigid body,

that is, ignoring the heading speed caused by the

deformation of the landing gear. According to the

principle of brake rotor inertia, the equation of wheel

dynamics is

J

MRN

J

MM

sgSj

−

=

−

=

1

μ

ω

&

(2)

g

RV

ω

=

(3)

By formula (1) ~ (3) :

hba

h

m

VKT

b

m

SVC

g

m

SVC

m

VKT

V

t

XV

Xy

XV

X

μ

ρ

μ

ρ

++

+

−

⎟

⎠

⎞

⎜

⎝

⎛

−

+

=

0

2

0

2

&

(4)

()

J

M

hba

hVKT

nJ

R

hba

bSVCmg

nJ

R

StXV

g

Xy

g

−

++

+

−

++

⎟

⎠

⎞

⎜

⎝

⎛

−

=

μ

ρ

μω

0

2

1

2

1

&

(5)

In the process of landing braking, the wheel

speed of aircraft is less than or equal to the

longitudinal speed of aircraft under the braking

torque, that is,

X

VV ≤

ω

, the rate of relative

movement is defined as slip rate, namely:

X

g

X

V

R

V

VV

ω

σ

ω

−=

−

= 1

(6)

The derivation of the above formula can be

obtained:

X

gX

X

g

X

g

V

RV

V

R

V

R

ωσ

ω

ωσ

&

−−

=

+−=

)1(

2

(7)

The formula (4) and formula (5) are put into the

above formula, and then:

S

X

g

S

X

g

X

g

XXV

X

M

JV

R

f

M

JV

R

JV

NR

m

NnFVKT

V

+=

+−

−−+

⋅

−

=

)(

1

2

10

σ

μ

σ

&

(8)

In which,

JV

NR

m

NnFVKT

V

f

X

g

XXV

X

1

2

10

1

)(

μ

σ

−

−−+

⋅

−

=

(9)

The definition of parameters in the above

formula is the same as (Wang Jisen, 2001; Qiu

Yanan, 2016) in the references.

2.2 Drive Mechanism and Actuator

Model

For aircraft hydraulic brake system, the drive

mechanism is composed of hydraulic servo valve,

which converts the brake current into brake pressure

via hydraulic servo valve and applies to the brake of

The Adaptive Control of Aircraft Brake Based on Asymmetric Barrier Lyapunov Function

103

the actuator to convert it into braking torque, which

interacts with the combined torque provided by the

ground, in order to decelerate the aircraft until it

stops the aircraft.

2.2.1 The mathematical model of brake

pressure servo valve

Electro-hydraulic servo valve is an important part of

the aircraft hydraulic control system, and the

pressure characteristics of electro-hydraulic servo

valve is one of the important features of the servo

valve by changing the input port of the control

current size and direction. The output pressure can

be changed in the size of the direction, according to

the nozzle baffle servo valve structure and working

principle

(Chen Zhaoguo, Li Zhigang, Huang Qi, 2005),

and the pressure equation of the dynamic equation

is:

c

e

t

q

f

L

ks

V

k

X

P

+

=

β

4

(10)

θ

rX

f

=

(11)

1

2

/1

2

++

⋅

=

Δ

s

kk

I

mf

tmf

ω

ξ

ω

θ

(12)

The anti-Laplace transformation of the formula

(10) is:

f

t

qe

L

t

ce

L

X

V

k

P

V

k

P

β

4

+−=

&

(13)

The formula (11) is brought intoit and then:

θ

β

t

qe

L

t

ce

L

V

rk

P

V

k

P

4

+−=

&

(14)

Similarly, the anti-Laplace transform of the

formula (12) is:

I

k

mfmf

mft

mfmf

mf

Δ⋅++−=

ξ

ω

θ

ξ

ω

θ

2

)(

2

&&

&

(15)

The meaning of the letters in the above formula

is described in

(Chen Zhaoguo, Li Zhigang, Huang Qi,

2005) of the references.

2.2.2 The mathematical model of brake

device

Through the overlap and installation of dynamic and

static disks, the brake device forms a larger friction

area, and absorbs the heat transformed by kinetic

energy in the process of aircraft braking, that is, the

so-called “hot reservoir”. The pressure-torque

characteristic of the braking device is one of the key

factors that influence the control performance of the

aircraft. The mathematic model is derived as

follows.

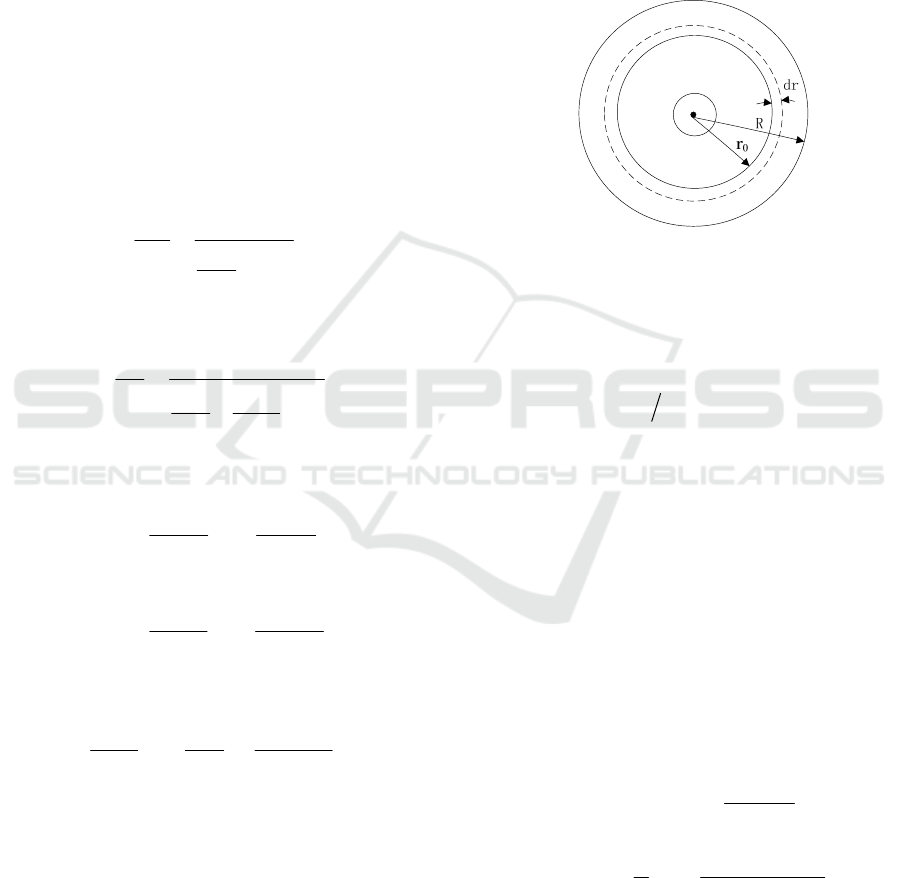
The friction outer radius of brake is defined as R, the

friction inner radius as

0

r , and the ring of the friction

surface is taken as

dr

, which is shown in Figure 1.

Figure 1: Diagram for friction surface of brake device

Assumptions: (1) the friction coefficient remains

constant during braking;(2) the thrust force of piston

on the brake disc is even.

The pistons thrust per unit area is:

()

[

]

π

⋅−=

2

0

2

rRSF

Tp

(16)

The ring

dr is taken, then the piston thrust

withstood by ring

dr

is:

drFdF

p

⋅=

(17)

The friction generated by piston ring

dr is:

rFdFdf

pss

π

μ

2dr ⋅⋅=⋅=

(18)

Torque generated by piston ring

dr

is

rdrFrdfrdM

pss

π

μ

2⋅⋅=⋅=

(19)

Then the torque generated from the upper piston

thrust

Rr →

0

is:

0

2

00

2

0

2

rR

r

3

2

r

2

0

+

++

=

−

⋅=

∫

RrR

S

dr

R

S

r

rdrFrM

Ts

R

r

T

s

R

r

pss

μ

πμ

(20)

In the formula:

s

μ

——friction coefficient of brake

disc,

()

vPf

s

,=

μ

ICECTT 2018 - 3rd International Conference on Electromechanical Control Technology and Transportation

104

T

S

——total piston thrust,

nSPS

LT

**=

L

P

——brake pressure;

S

——piston area;

n

——piston number.

Namely, the relationship between brake torque

and brake pressure is:

LLsS

KPP

rR

rRrR

SM =

+

++

=

0

2

00

2

n

3

2

μ

(21)

In which,

0

2

00

2

n

3

2

rR

rRrR

SK

s

+

++

=

μ

The overall nonlinear mathematical model of

aircraft brake control system in the above can be

sorted out:

⎪

⎩

⎪

⎨

⎧

Δ⋅++−=

+−=

+=

I

k

V

rk

P

V

k

P

JV

KR

f

mfmf

mft

mfmf

mf

t

qe

L

t

ce

L

X

g

ξ

ω

θ

ξ

ω

θ

β

σσ

2

)(

2

4

)(

2

&&

&

(22)

Equation (22) can then be written as the

following equation of state with strict feedback,

namely:

⎪

⎩

⎪

⎨

⎧

=

+=

=+=

+

,1

33333

1

,)()(

,2,1,)()(

xy

uxgxfx

ixxgxfx

iiiiii

&

(23)

In which:

σ

=

1

x

)(

1

σ

ff =

JV

KR

g

X

g

=

1

L

Px =

2

L

t

ce

P

V

k

f

β

4

2

−=

t

qe

V

rk

g

β

4

2

=

θ

=

3

x

)(

2

3

mfmf

mf

f

ω

θ

ξ

ω

&&

+−=

mfmf

mft

k

g

ξ

ω

2

3

=

Iu Δ=

3 THE CONSTRAINT

CONTROLLER DESIGN OF

SLIP RATE BASED ON

ASYMMETRIC BARRIER

LYAPUNOV FUNCTION

Considering the stability and instability of the slip

ratio in the aircraft anti-skid braking system, the

control method is designed as shown in Figure 2.

The slip ratio is divided into the stable and unstable

regions by the slip ratio

*

σ

corresponding to the

maximum combination coefficient

max

μ

.When

*

0

σ

<< A

is for the stable area, then

1

*

<< A

σ

for the unstable area. The purpose of

the constraint adaptive controller design for slip rate

based on asymmetric barrier Lyapunov function is to

ensure that the brake control system works at the

optimal slip ratio

*

σ

and the working range is

confined in the stable region of the tire runway

model. Meanwhile, the tracking error of slip

ratio

σ

converges to a small set of zeroes.

Figure 2: Friction model for tire runway

The error items

*

1

σσ

−=−=

d

yyS ，

iii

zxS −=

and 3,2=i are defined. During the

operation for the entire control system of aircraft

brake, the adaptive controller will stop when the

aircraft reaches the non-slip failure speed (typically

25Km / h), so the speed of aircraft

0>

X

V

.Then

for all

0,0 >>

i

gt

and 3,2,1=i is known, which

is a prerequisite for the control method.

The initial value

*

)0(

σσ

< of slip rate is

defined. The constant

25.0

1

=

c

k is selected as the

output constraint for the upper bound of slip rate,

and the output constraint

)0(

2

σ

=

c

k for the lower

bound of the slip rate. Then from the constrained

lower bound

)0()(

*

21

σσ

−=−=

cda

kytk and

The Adaptive Control of Aircraft Brake Based on Asymmetric Barrier Lyapunov Function

105

the constrained upper

bound

*

111

)(

σ

−=−=

cdcb

kyktk of

corresponding tracking error

1

S ,it is easy to judge

that both

)(

1

tk

a

and )(

1

tk

b

are bounded.

Virtual filter function

2

z

is introduced, and

from:

iiii

zz

α

τ

=+

+++ 111

&

，

)0()0(

1 ii

z

α

=

+

，

2,1=i

The first-order filter error is obtained:

iii

z

α

χ

−=

++ 11

，

1

+

−=

i

z

τ

χ

&

Based on asymmetric barrier Lyapunov function,

the following Lyapunov function is constructed:

⎪

⎩

⎪

⎨

⎧

+=

++=

+

−

+

−

=

2

323

2

3

2

212

2

1

2

1

2

1

2

1

2

1

2

1

2

1

2

1

2

1

2

1

)(

log

2

)(

log

2

1

SVV

Stk

tk

q

Stk

tk

q

V

b

a

χ

(24)

In which,

⎩

⎨

⎧

≤

>

=

0,0

0,1

1

S

q

Based on the above analysis and combined with

the characteristics of slip control for aircraft braking

control system, the constraint control law of slip

ratio for the braking control system is obtained:

[]

⎪

⎩

⎪

⎨

⎧

⎥

⎦

⎤

⎢

⎣

⎡

−−−−=

⎥

⎦

⎤

⎢

⎣

⎡

−−

−

⎥

⎦

⎤

⎢

⎣

⎡

−

−−=

+−−=

=

==+

++++

3

22333

3

2

1

2

1

2

1

2

1

1122

2

111

1

1111

1

)

)(

(

1

)

)(

1

(

1

2,1

),0()0(,

τ

χ

τ

χ

α

αατ

SgfSk

g

u

f

Stk

q

Sg

g

Stk

q

SgSk

g

yfSk

g

i

zzz

b

a

d

iiiiii

&

(25)

Formula (23) is substituted into the above

formula, the output restraint control law of slip ratio

for the aircraft anti-skid braking system is obtained

based on asymmetric barrier Lyapunov function as

follows:

[]

⎪

⎩

⎪

⎨

⎧

⎥

⎦

⎤

⎢

⎣

⎡

−−

⎥

⎦

⎤

⎢

⎣

⎡

++−=

⎥

⎦

⎤

⎢

⎣

⎡

−+

−

−−

−

−=

+−−=

=

==+

++++

3

2

33

2

1

2

1

22

2

1

2

1

2

111

1111

42

)(

2

4

)

)(

(

44

)

)(

1

(

4

)(

2,1

),0()0(,

τ

χ

β

ω

ξ

ω

θ

ξ

ω

ξ

τ

χ

β

ββ

β

α

σα

αατ

S

V

rk

k

Sk

k

u

P

V

k

rk

V

Stk

q

JV

KSR

rk

V

rk

SkV

Stk

q

JV

KSR

rk

V

yfSk

KR

JV

i

zzz

t

qe

mft

mfmf

mf

mft

mfmf

L

t

ce

qe

t

bX

g

qe

t

qe

t

a

X

g

qe

t

d

g

X

iiiiii

&&

&

(26)

4 RESULT ANALYSIS OF

PERFORMANCE SIMULATION

Through the simulation of the entire anti-skid

braking system of aircraft with Matlab, there are the

following two hypotheses: (1) assuming that the

aircraft does not perform turning operations during

braking, but maintains a straight-line movement

landing;(2) assuming that the load and grounding

conditions of both left and right main landing gears

are the same, and the brake control system is

simplified into a single-wheel control model. Based

on the above assumptions, the control law based on

the slip rate constraint and the control law of the

traditional “PD + PBM”were simulated and

analyzed under different runway conditions. The

simulation curves of the wheel speed and the brake

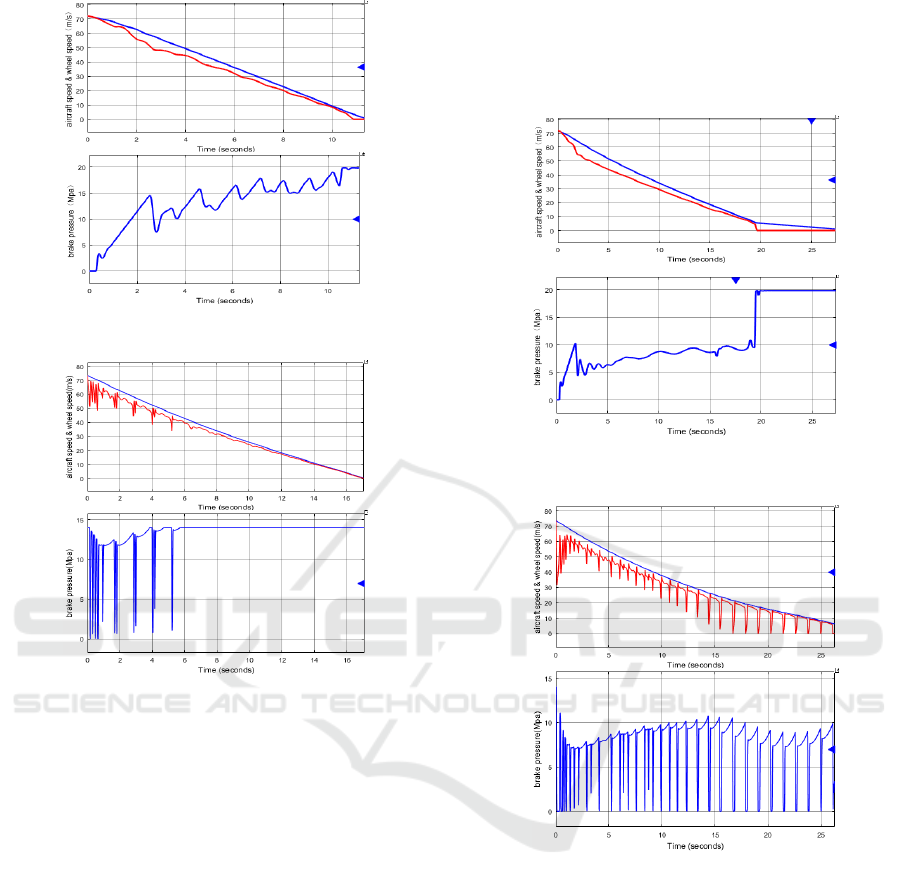
pressure are seen in Figure 3 ~ Figure 5.

ICECTT 2018 - 3rd International Conference on Electromechanical Control Technology and Transportation

106

(a) Simulation curves of adaptive control law

(b) Simulation curves of traditional PD + PBM control law

Figure 3: Simulation results under dry runway conditions

It can be seen from Figure 3, the adaptive control

algorithm based on the slip rate constraint can be

compared with the traditional PD + PBM control

algorithm under the condition of dry runway. The

brake control system under the adaptive control

algorithm can be adjusted in the maximum range (0-

21Mpa) within the regulation of brake pressure. The

maximum can be adjusted to 20.8Mpa, so as to

obtain a larger braking torque, braking efficiency is

higher, the slip rate of about 95% efficiency, and

braking distance of 372m; and throughout the

braking process, the system can work

near the optimal slip ratio corresponding to the

maximum binding coefficient and always stay in a

stable region of the curve

σ

μ

−

. The slip rate

always fluctuates around 0.13 except for the initial

slow pressure rise until the anti-slip is released.

Under the traditional PD + PBM control algorithm,

the maximum braking pressure is limited to

13Mpain order to prevent torque charge, the

utilization rate of the ground is reduced, the system

cannot obtain the maximum braking torque, and the

braking distance increases to 574.4mrelative to the

adaptive control algorithm, slip rate efficiency is

about 85.5%, and braking efficiency is significantly

reduced.

(a) Simulation curves of adaptive control law

(b) The Simulation Curves of Traditional PD + PBM

Control Law

Figure 4: Simulation results under wet runway conditions

It can be shown in Figure 4 that the combination

coefficient provided by the ground reduces under

wet runway conditions. To balance the matching

torque, the brake pressure provided by the brake

control system reduces accordingly. The maximum

brake pressure is down to about 8Mpa. However,

during the entire braking process, the brake pressure

under the adaptive control algorithm based on the

slip rate constraint can respond quickly and can be

accurately adjusted within a small range. In addition

to the slowly rising phase of the initial pressure, the

slip rate always fluctuates around 0.15 until the slip

at the 19.4s is released. No deep slippage appears in

The Adaptive Control of Aircraft Brake Based on Asymmetric Barrier Lyapunov Function

107

the process of entire braking, which can maintain a

higher braking efficiency. The braking efficiency is

about 88% and the braking distance 711.8m; but

under the wet runway condition, the wheel in the

traditional PD + PBM control is always in a slippery

condition, and many deep slippage occurs, which

makes the tire more wear and tear and reduces the

service life of the tire and the braking efficiency.

The braking efficiency is 74.8% and the braking

distance is 871.1m.

(a) Simulation curves of adaptive control law

(b) Simulation curves of traditional PD + PBM control law

Figure 5: Simulation results under Ice runway conditions

As can be seen from Figure 5, the combination

coefficient provided by the ground significantly

reduces under the ice runway conditions. In order to

prevent the occurrence of bodily defects and locking,

the maximum braking force of the brake device

applied by the brake control system is significantly

reduced, about 5Mpa. However, the adaptive control

algorithm based on slip rate constraint is smoother

throughout the braking process and does not appear

deep slipping. The braking time is 32.8s and the

braking distance is 883.2m. However, the braking

time of the conventional PD + PBM control law is

52.3s and the braking distance is 1543m. The

response of the brake pressure regulation is slow

during the entire braking process. There is deep

slippage, which is worse than the adaptive control

algorithm based on the slip ratio constraint.

5 CONCLUSION

Based on the analysis of the non-linear mathematic

model for the aircraft anti-skid braking system, the

author puts forward an adaptive control method of

slip ratio constraint based on asymmetric barrier

Lyapunov function. The simulation tests show that

under different conditions of dry, wet and ice

conditions:

(1) The anti-skid braking system of aircraft has

the characteristics of high-order non-linear

parameters such as time-varying. Due to the

influence of runway environment, design parameters

of driving mechanism and actuator, aerodynamics

and other factors, linear control theory cannot

guarantee that brake operating point is located in a

stable region.

(2) Compared with the traditional PD + PBM

control algorithm, the adaptive control of slip rate

constraint based on the asymmetric Lyapunov

function can quickly adjust the brake pressure so

that the system can maintain the curve

σ

μ

−

under

all conditions in the stable area, the system can make

full use of the frictional resistance provided by the

ground, make the whole brake control system and

the wheel have a good match, and reduce the

frequency of skidding, shorten the braking distance

and improve the braking efficiency.

(3) Through the application of adaptive control

method, no slippage or lock-up occurs, the wear on

the braking device is reduced and the service life of

the brake disc is increased, thereby the economy of

use is improved.

To sum up, the adaptive control method of slip

rate constraint asymmetric barrier based on

Lyapunov function is a design method with high

performance and economy, which will be an

important evaluation index in the field of civil

aircraft development. Therefore, this method is

proposed to provide the direction and basis for

engineering application in the field of adaptive full-

regulation control of aircraft skid braking system.

ICECTT 2018 - 3rd International Conference on Electromechanical Control Technology and Transportation

108

REFERENCES

AC NO.25-7A ， Flight Test Guide for Certification of

Transport Category Airplanes.FAA.

TANELLI M, ASTOLFI A, SAVARESI S M,

2008.Robust nonlinear output feedback control for

brake by wire control systems[J]. Automatica. Vol.44,

p:1078~1087.

R.Babuska, H.B.Verbruggen, 1996.An Overview of Fuzzy

Modeling for Control. Control Engineer Practice.

p:1593~1606.

MI C T, LIN H, ZHANG Y, 2005.Iterative learning

control of antilock braking of electric and hybrid

vehicles[J]. IEEE Transactions on Vehicular

Technology. Vol.54, p: 486-494.

BASLAMISLI S C，K SE I E, ANLAS G,2007.Robust

control of anti-lock brake system[J]. Vehicle System

Dynamics, Vol. 45,p: 217-232.

TANELLI M, FERRARA A, 2013. Switched second-

order sliding mode control with partial information:

Theory and application[J]. Asian Journal of Control.

Vol.15,p: 20-30.

CHO D-W, CHOI S, 1999.Control of wheel slip ratio

using sliding mode controller with pulse width

modulation[J]. Vehicle System Dynamics. Vol.32,p:

267-284.

CHOI S, CHO D-W, 2001.Design of nonlinear sliding

mode controller with pulse width modulation for

vehicular slip ratio control[J]. Vehicle System

Dynamics, Vol.36,p: 57-72.

HEBDEN R G, EDWARDS C, SPURGEON S K,

2004.Automotive steering control in a split-manoeuvre

using an observer-based sliding mode controller[J].

Vehicle System Dynamics, Vol.41,p:181-202.

Shi Wei, Liu Wensheng, Chen Jianqun, 2012.Application

of Model Free Control Technology on the Aircraft

Anti-skid Brake Systems. Computer Measurement &

Control. Vol.20,p:1552-1554.

Wang Jisen, 2001.Nonlinear Control Theory and its

Application to Aircraft Antiskid Brake Systems [D].

Doctoral Thesis of Northwestern Polytechnic

University.

Qiu Yanan, 2016.Constrained Control for Nonlinear

Systems and its Applications [D]. Doctoral Thesis of

Northwestern Polytechnic University .

Chen Zhaoguo, Li Zhigang, Huang Qi, 2005.Study on the

Pressure Characteristics of the Electro-hydraulic Servo

Valve of Two Nozzle Baffles. [J]. Engineering

Machinery.Vol. 36 ,p:28-30.

Chen Xiaolei, 2016.Research on Control Strategy of

Electromechanical Actuation Servo System for More

Electric Aircraft [D]. Doctoral Thesis of Northwestern

Polytechnic University .

SU Jun-ming, etc., 2011. Effects of braking velocity and

pressure on aircraft brake discs' friction and wear

properties [J]. Materials Science and Engineering of

Powder Metallurgy. Vol. 16,p:212-217.

Xiong Xiang, 2004.Investigation of Braking Properties of

Carbon-Carbon Composites [D]. Doctoral Thesis of

Central South University.

The Adaptive Control of Aircraft Brake Based on Asymmetric Barrier Lyapunov Function

109