Application Research on Developed Chaos-Wasp Colony
Algorithm Used in Suspension-Parameter Optimization
Hai
t
ao Zhang
1
, Hong Gao
2
, Xinlin Hun
1
and Aiguo Wang
1
1
Department of Automobile Engineering, Anhui Technical College of Mechanical and Electrical Engineering, Wuhu,
241002, China
2
School of Mechanics and Automobile Engineering, Anhui Polytechnic University，Wuhu ,241000, China
Z
han
g
haitao5238
@
163.com
Keywords: Parameter matching of suspension, Artificial wasp colony algorithm, Chaos factor, Optimization method of
chaos-wasp colony algorithm.
Abstract: Aimed at parameters matching of automobile suspension system, this paper was presented an approach to
optimize suspension system parameters based on developed chaos-wasp colony algorithm . Firstly, chaos factors
were initialized through cube map; Balance of local and global searching of artificial wasp colony algorithm was
realized on the basis of inertia weight of exponential decline; Early maturing was judged by fitness variance
values. Secondly, dynamic models of quarter suspension were established and Matlab/Simulink software was
employed to conduct the simulation experiments by taking integral white noise as road surface input. Results of
simulation experiments indicated that developed chaos-wasp colony algorithm was better than tradition
algorithms and normal artificial wasp colony algorithm.
1 INTRODUCTION
To a great extent, the comfort level of a rid and
riding performance of a car depends on the
suspension system. Therefore, research on
suspension system was critical to improve them.
Nowadays, it was focused on the control strategy of
active suspension system. However, the vehicle
suspensions were mainly based on the passive
suspensions. Thus how to determine the stiffness
value of the spring and the damping value of the
absorber were greatly important. Pan (2005)
optimized the automobile suspension system
parameter by the optimal control theory and the least
square method; Xu (2012) realized the optimization
of the main parameters of hydro -pneumatic
suspension based on the genetic algorithm; Li(2015)
applied the genetic optimization algorithm and the
decision-making control theory to optimize the
automobile suspension system parameter;
Pang(2014) explored the optimization of the
parameters of the vehicle air suspension system,
using the general genetic algorithm and the
improved multi-objective adaptive optimization
algorithm; Ma(2013) investigated the optimization
of parameters of vehicle suspension system,
employing the two methods of ideal modification
parameter selection and optimal modification
parameter selection.
This paper will contribute to the artificial bee
colony algorithm based on the improved chaos
strategy to avoid premature convergence and local
optimum. Taking optimization parameter design and
simulation with 4 degree of freedom 1/2 suspension
system for example, this paper will verify the
improved chaos artificial bee colony algorithm
compared with the traditional one has some
advantages.
2 IMPROVED CHAOTIC BEE
COLONY OPTIMIZATION
ALGORITHM
2.1 Artificial Bee Swarm Optimization
Algorithm
Artificial bee colony algorithm (ABC) (Kuang, 215)
was a kind of optimization algorithm with global
searching ability and fast convergence rate, which
150
Zhang, H., Gao, H., Hun, X. and Wang, A.
Application Research on Developed Chaos-Wasp Colony Algorithm Used in Suspension-Parameter Optimization.
In 3rd International Conference on Electromechanical Control Technology and Transportation (ICECTT 2018), pages 150-155
ISBN: 978-989-758-312-4
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

was simulated by bee swarm intelligence. In ABC,
Bee colony was composed of leading bee, following
bee and reconnaissance bee. To search for honey
containing more food sources ,leading bee will
constantly update their food sources .After all the
leading bee search , they will dance to share with
following bee the information of food source
position and quantity of honey containing .Then
following bee choose the food source based on the
yield of the food source, and the more honey you
have in the source, the more likely you were to be
selected. Then they will proceed to the next round of
search in the same way. So the algorithm was as
follows:
Step1: initialize the population and obtain initial
solution by formula (1).
()
()
jjjj
i
xxrandxx
maxminmin
1,0 −+=
（1）
Step2: leading bee search for new solutions
Newfit(i) in feasible scope according to formula(2),
and calculate new fitness value of Newfit (i). If
Newfit (i) > Fit (i), update new solution
i
v ,
otherwise the number of failed Lost (i) plus 1.
()
()
j
k
j
i
j
i
j
i
xxrandxv −+= 1,0
（2）
Calculate the selection probability of each
individual according to formula(3)
)3(
)(
)(
1
∑
=
=
N
i
i
iFit
iFit
P
Step3: following bee search new solution
according to the selection probability P
i
and formula
(2) within the scope of the feasible solution.If
Newfit (i) > Fit (i), update new solution
i
v ,
otherwise the number of failed Lost (i) plus 1.
Step4: if Lost (i)>limit, abandon the solution,
and leading bee was into reconnaissance bee finding
new solutions according to equation (1).
Step5: if the fitness of the solution satisfies the
preset accuracy or reaches the maximum number of
iterations, the loop ends and the optimal solution
was output.
2.2 Improvedare Algorithm
(1)Chaotic Operator
There many ways to generate chaotic variables,
which logistic mapping and cubic mapping to
generate it were most commonly used. The cubic
mapping helps to maintain the uniformity of
chaotic variables , so this paper adopts the method of
cubic mapping of chaos operator to initialize (Zhou,
2012). The cubic mapping was defined by
()
⎩
⎨
⎧
=<<−
−=
+
L,2,1,011
34
3
1
ny
yyy
n
nnn
（4）
Then the initial value
j
i
X
of the chaos artificial
bee colony algorithm was given by
() ()
Ni
xx
yxX
jj
j
i
jj
i
,,2,1,0
2
1
minmax
min
L=
−
++=
（5）
Where N was colony size .
min max
,
jj
x
x were colony
variable minimum and maximum value ，
respectively.
j
i
y
was chaotic variable value.
（2）Nonlinear Inertia Weight
The above analysis shows that the key to the
artificial bee colony algorithm was the quality
source position update. Then quality source
position
v was deduce that
()()
j
it
j
b
j
it
j
ib
j
it
j
it
XGrXPrvv −+−+=
+ 22111
θθω
（6）
Where
t was the number of iterations,
T
was the
total number of iterations,
j
it
X was the initial
variable，
j
it
v was locator variable，
1
θ
and
2
θ
were
acceleration factor of the algorithm, which value 1.8
～2.
1
r and
2
r were random factor, which value 0～
1.
j
ih
P was position variable of the best historical
position,
j
b
G was position variable of the best global
position.
ω
was nonlinear inertia weight of the
algorithm.
Note that large inertia weight factor was
conducive to improve the global search ability of the
algorithm and small inertia weight factor was
beneficial to improve the local search ability. Then
the exponentially decreasing inertia weight to
balance the local and global search capabilities of
the artificial bee colony algorithm was defined by
()
()
min
40
minmax
2
ωωωω +−=
−
T
t
e
（7）
Where
9.0,4.0
maxmin
==
ω
ω
.
(3)Early Maturity Judgment Mechanism
The artificial bee colony algorithm trends to fall
into the local optimum state and the premature
phenomenon in the search process. Fitness variance
reflects the degree of convergence of a colony.
Fitness variance
2
σ was given by
[]
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=
−=
≤
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=
∑
∑
=
=
N
i
iavg
avgi
N
i
avgi
f
N
f
ffabsf
f
ff
1
1
22
1
)))(max(,1max(
σσ
（8）
Where
i
f was the fitness of nectar.
avg
f was current
Application Research on Developed Chaos-Wasp Colony Algorithm Used in Suspension-Parameter Optimization
151

average fitness of bee colonies.
[
]
2
σ
was premature
judgment threshold. The bigger
2
σ
was, the bee
swarm was in the random search stage; on the other
hand, the bee colony tends to converge, and the local
optimization was easier. Then it was necessary to
provide a perturbation mechanism for the algorithm
to make it jump out of the local optimum position
and search the global optimum position. Firstly, the
chaotic operator was initialized by cubic mapping
method; Secondly, a random chaotic sequence to
meet colony dimensions was provided, according to
formula (6) chaotic sequences in each dimension
were changed into numerical position variables in
bee colony algorithm; Finally ， With method of
variance the optimal nectar in each dimension was
found , and the random chaotic sequence was
iteratively updated. Consequently, the global
optimum was achieved.
2.3 Improved Chaotic Bee Colony
Optimization Algorithm
Based on the above analysis, improved chaotic
particle swarm optimization was provided, which
balances the local and global search capabilities of
the artificial bee colony algorithm by the cubic
mapping method adopted to initialize the chaos and
the inertia weight of exponential decreasing . The
specific operation process was as follows：
Step1 ： assume that
M
was population size ，
min
ω
，
max
ω
were respectively the minimum and
maximum of inertia weight factor, T was the total
number of colony iteration,
[
]
2
σ
was premature
judgment threshold and
21
,
θ
θ
were the acceleration
factor of the algorithm.
Step2 ： initialize the chaotic sequence by the
formula (4) , convert it to variable value in the hive
dimension by the formula (5), evaluate the fitness
value of honey, set the initial historical best position
nectar variables
ib
P
,
and find initial global best
position variable
b
G
.
Step3：Update the inertia weight factor of the
algorithm by the formula (7) and the location of the
algorithm by the formula (6), calculate the updated
fitness value of honey, renew the value
ib
P
,
b
G
,
calculate bee colony fitness variance
2
σ by the
formula (8) and make a premature judgement. If the
algorithm has been in the state of stagnation, we
execute step4. Otherwise, the step5 is executed.
Step4：Reproduce a new nectar according to
the formula (4) and (5), evaluate new nectar fitness,
find the optimal location of nectar , Randomly
replace some nectar source, and execute step5.
Step5 ： If the fitness value meets the some
accuracy or reaches the maximum number of
iterations , the loop ends and outputs the optimal
value. Otherwise, the step3 is executed.
3 APPLICATION RESEARCH
ON DEVELOPED CHAOS-
WASP COLONY ALGORITHM
USED IN SUSPENSION-
PARAMETER
OPTIMIZATION
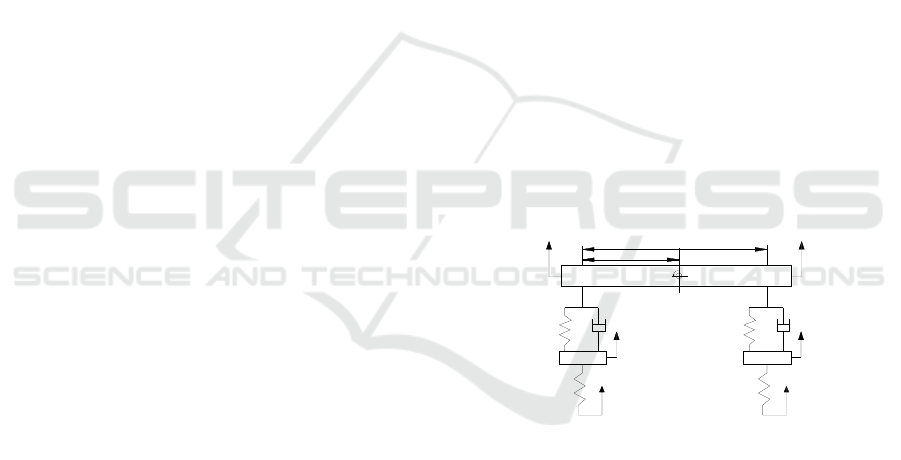
3.1 Models of Half Suspension
The suspension dynamic model of half car was
displayed in Fig.1,in which motion equations of 4
degrees of freedom entire car suspension system
were written in two steps.Given centroid was
[]
T
cC
xX φ =
,2 motion equations of car body could
be deduced:
L
b
x
t2
x
t1
x
r2
x
r1
k
t2
k
t1
k
s1
k
s2
c
s2
x
s
x
s1
m
t2
x
c
m
s,
J
Φ
,Φ
c
s1
m
t1
Fig .1 Half vehicle model of passive suspension
0)()(
)()(
222111
222111
=−+−
+−+−+
tsstss
tsstsscs
xxkxxk
xxcxxcxm
&&&&&&
（9）
0))(()(
))(()(
222111
222111
=−−+−
−−−+−−
bLxxkbxxk
bLxxcbxxcJ
tsstss
tsstss
&&&&
&&
φ
φ
（10）
The motion equations of 2 unsprung weight
systems were:
0)()(
)(
111111
11111
=−+−
+−+
rttsts
ststt
xxkxxk
xxcxm
&&&&
（11）
0)()(
)(
222222
22222
=−+−
+−+
rttsts
ststt
xxkxxk
xxcxm
&&&&
（12）
⎩
⎨
⎧
−+=
−=
φ
φ
)(
2
1
bLxx
bxx
cs
cs
（13）
ICECTT 2018 - 3rd International Conference on Electromechanical Control Technology and Transportation
152

where
s
m
was sprung weight of half car;
φ
J
was
rotary inertia of car body;
c
x
was centroid
displacement;
φ
was Longitudinal pitch angle of
car body;
L
was the distance between the front and
rear ;
b
was the distance from centroid to the front
axle of the automobile;
21
,
tt
mm
were unsprung
weights;
21
c,c
ss
were damping
coefficient;
21
k,k
ss
were suspension spring
parameters;
21
x,x
tt
were upsprung weight
displacement;
21
x,x
ss
were sprung weight
displacement;
21
k,k
tt
were tire stiffness
parameters.
21
x,x
rr
were road excitation
displacements.
3.2 Optimization Variables
To a great extent, the vehicle ride comfort and riding
performance of a car depends on the suspension
system.And suspension was mainly composed of
shock absorber and spring,Therefore, the stiffness
value of the spring and the damping value of the
damper were taken as design variables:
[]
T
i
ckckx
2211
=
（14）
3.3 Objective Function
In order to make the vehicle ride performance and
riding comfort better, the objective function of the
vehicle suspension system optimization algorithm
was set up as follows
)]([
)]([
)]([
)]([
)15(
)]([
)]([
)]([
)]([
min
2
2
2
2
1
1
1
1
XcRMS
XcRMS
XkRMS
XkRMS
XcRMS
XcRMS
XkRMS
XkRMS
J
passpass
passpass
+
++=
Where
)]([
1
XkRMS
,
)]([
1
XcRMS
,
)]([
1
xkRMS
pass
,
)]([
1
xcRMS
pass
,
2
[()]
R
MS k X
,
2
[()]RMS c X
,
2
[()]
pass
RMS k x
,
2
[()]
pass
RMS c x
were
root mean square values of the passive suspension
spring stiffness and damping obtained before and
after the suspension of the optimized and the
traditional one ,respectively.
Based on the design variables and objective
functions above, the optimization model of passive
suspension system was established as follows
[]
)16(
)]([
)]([
)]([
)]([
)]([
)]([
)]([
)]([
min
2
2
2
2
1
1
1
1
2211
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
+
++=
=
XcRMS
XcRMS
XkRMS
XkRMS
XcRMS
XcRMS
XkRMS
XkRMS
J
ckckx
passpass
passpass
T
i
4 SIMULATION
Referring to Fig. 1, the model was based on formula
(9)- (13), and establishes the corresponding
simulation model using the matalb/simulink module,
as shown in Figure 2.
In order to check whether optimal designed in
this paper could test working effect of optimization
of passive suspension, simulation experiments on
this system were carried the experiment took C road
surface as input and
hkmV /40=
as the vehicle’s speed.
The car type parameter were shown.
Fig.2 Simulation model
Application Research on Developed Chaos-Wasp Colony Algorithm Used in Suspension-Parameter Optimization
153

s
m720kg=
;
t1
m40kg=
;
t2
m45kg=
;
2
J 1222kg m
ϕ
=⋅
;
2.8
L
m=
；
1.3bm=
；
1
k 170 /00
s
N
m=
；
1
c 250 /0
s
Ns m=
；
1
k 200 /000
t
N
m=
；
2
k 220 /00
s
Nm=
；
2
c200/0
s
Ns m=
；
1
k200 /000
t
Nm=
； The search range of k
1
、 c
1
、
k
2
、 c
2
were
6
110
⎡⎤
⎣⎦
， T=100 ，
min
0.4 ω =
，
max
0.9 ω =
，
12
1.8 θθ ==
，
2
0.01 σ
⎡⎤
=
⎣⎦
and the simulation results
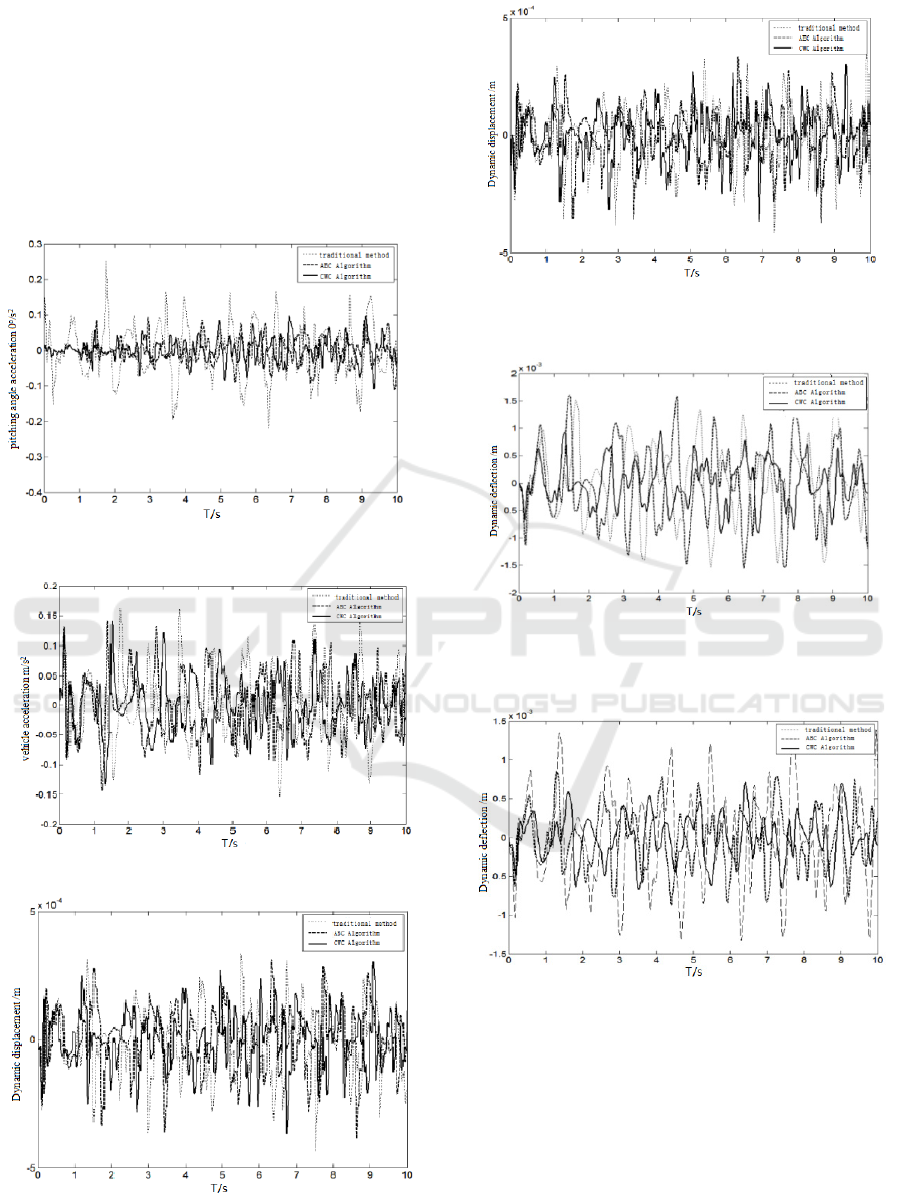
were shown in Fig. 3 to Fig. 8.
Fig.3 Simulation curve of pitching angle acceleration
Fig.4 Simulation curve of vehicle acceleration
Fig.5 Dynamic displacement simulation curves of front
suspension
Fig.6 Dynamic displacement simulation curves of rear
suspension
Fig.7 Dynamic deflection simulation curves of front
suspension
Fig.8 Dynamic deflection simulation curves of rear
suspension
From Fig. 3 to Fig. 8, The vehicle suspension
based
on the chaotic bee colony algorithm significantly
reduces the vertical acceleration of the car body, the
tire moving position and the dynamic deflection of
the suspension.
ICECTT 2018 - 3rd International Conference on Electromechanical Control Technology and Transportation
154

5 CONCLUSION
In this paper, an improved chaotic bee colony
algorithm was presented , which avoids local
optimization and premature convergence of the
algorithm. The parameters of the passive suspension
system of the 4 degree of freedom 1/2 body model
were optimized, and the corresponding simulation
model was established by using matlab/simulink
software. The simulation shows that the performance
of the suspension system parameters obtained with
the improved artificial bee colony algorithm was
better than the traditional and the artificial bee
colony algorithm; This method can also shorten the
cycle and cost of automobile suspension design; It
lays a theoretical foundation for the improvement of
vehicle ride comfort and handling stability and the
application of chaotic bee colony algorithm.
ACKNOWLEDGEMENTS
The work was supported by the Key project of Anhui
Provincial Department of education's natural science
(No.KJ2016A138&KJ2017A753)
REFERENCES
PAN Guojian.Optimal Control Method for Optimization of
Vehicle Suspension Parameters[J],Transactions of the
Chinese Society for Agricultural Machinery.2005
(11):156～160.
XU Dao-lin.Parametric optimization of hydro-pneumatic
suspension of a heavy mining dumper[J],Journal of
Vibration and Shock.2012 (24):98～101.
LI Zhongxing.Parameter Opimization and Control of Air
Suspension with adjustable auxiliary
Chamber[J],Automotive Engineering.2015 (8) ：
941～945.
Pang Hui. PENG Wei,YUAN Yuan. Multi-objective
optimization of pneumatic suspension parameters for
heavy vehicle under random excitation[J].Journal of
Vibration and Shock.2014 (6):156～160.
Ma Kai, Guan Xin ,Li Peng. Parameter Selection Method
in Optimization of Suspension Kinematics
Characteristics[J].Automotive Engineering.2013
(6):516～520.
KUANG Fang-jun.Hybridization algorithm of Tent chaos
artificial bee colony and particle swarm
optimization[J],Control and Decision.2015 (5):839～
847.
ZHOU Yan.Chaos particle swarm optimization based on
the adaptive inertia weight[J],Journal of Shandong
University( Natural Science).2012 (3)：27～32.
ZHANG Liang'an.Dimensional Synthesis of Ahut-Delta
Parallel Mechanism Based on Improved Chaotic
Particle Swarm lgorithm[J],Transactions of the
Chinese Society for Agricultural
Machinery.2015(8):344～351.
Application Research on Developed Chaos-Wasp Colony Algorithm Used in Suspension-Parameter Optimization
155