PID Control for the Vehicle Suspension Optimized by the PSO
Algorithm
Yongdong Xie
1
and Jie Meng
2
1
Suzhou Institute of Construction & Communications, Jiangsu Union Technical Institute ， Jiangsu Suzhou, China
2
School of automotive Engineering, Changshu Institute of Technology, Changshu215500, China
Keywords: Suspension, PSO algorithm, PID controller, Automotive control, performance.
Abstract: To solve the problems of the PID controller when it is used for the vehicle suspension, a method using the
PSO algorithm is designed. This method utilizes the global searching strategy of the PSO algorithm to
design and optimize the parameters of the target function for the suspension performance indexes matrix.
And then a simulation experiment is provided. The simulation results show that the performances of the
actively controlled vehicle suspension using the PID controller optimized by the PSO algorithm can be
greatly improved compared to the suspension controlled by the normal PID controller and the passive one. It
means that the problems of defining the weight matrices are well solved and the advantage of the normal
PID controller is utilized sufficiently.
1 INTRODUCTION
The suspension system is such an important
component of the vehicle, that its performance
significantly affects the vehicle ride comfort,
operation and stability. The traditional passive
suspension is generally composed of the elastic
component and damping components with the fixed
parameters. Such suspension systems are generally
designed to adapt to a certain type of road, so the
vehicle performance is restricted obviously. In
recent years, with the rapid development of the
electronic technology, testing techniques, and
system dynamics theories, the semi-active or active
vehicle suspension systems have been developed
based on the active vibration-isolation theory
(Zhang, 2013; Zhao,2011; Zhang, 2013; Chai, 2010;
Liu, 2010).
The popular vehicle suspension control strategies
include the Neural Networks Fuzzy Control,
Optimal Control, Immune Control, PID control, and
Fuzzy PID Control and etc.
The PID control is a popular method used in
industry due to its advantage. But the control effects
greatly depend on the PID parameters. As to the
active vehicle suspension, the control objects
include the body vertical acceleration, the
suspension dynamic travel distance and the tire’s
dynamic load. And these three often conflict with
each other. So, the parameters setting of the PID
controller is of greatest significance. The traditional
parameters setting method include the
Ziegle-Nichols method, the experience piece-try
method and etc. But these methods all have great
blindness, therefore the good PID parameters can
not be achieved and the optimum performances can
not be realized.
In 1995, Dr. Eberhart and Dr. Kennedy provided
a new theory-Particle Swarm Optimization(PSO)
based on the Swarm Intelligence Theory. This
method uses the swarm competition and cooperation
to produce swarm intelligence which guides and
optimize the value search. The PSO algorithm has a
quicker rate of convergence compared to the Genetic
Algorithm (GA). Meanwhile, its algorithm is simple
and it can be realized easily(Wang, 2006).
To solve the problems of the PID control used
for the vehicle suspension, the PSO method is
adopted to optimize the PID parameters. And the
system control model is set up by Matlab/simulink
together with simulation experiment. The simulation
results show that this active suspension can achieve
better vehicle ride compared to the normal PID
controller and the passive one.
172
Xie, Y. and Meng, J.
PID Control for the Vehicle Suspension Optimized by the PSO Algorithm.
In 3rd International Conference on Electromechanical Control Technology and Transportation (ICECTT 2018), pages 172-177
ISBN: 978-989-758-312-4
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

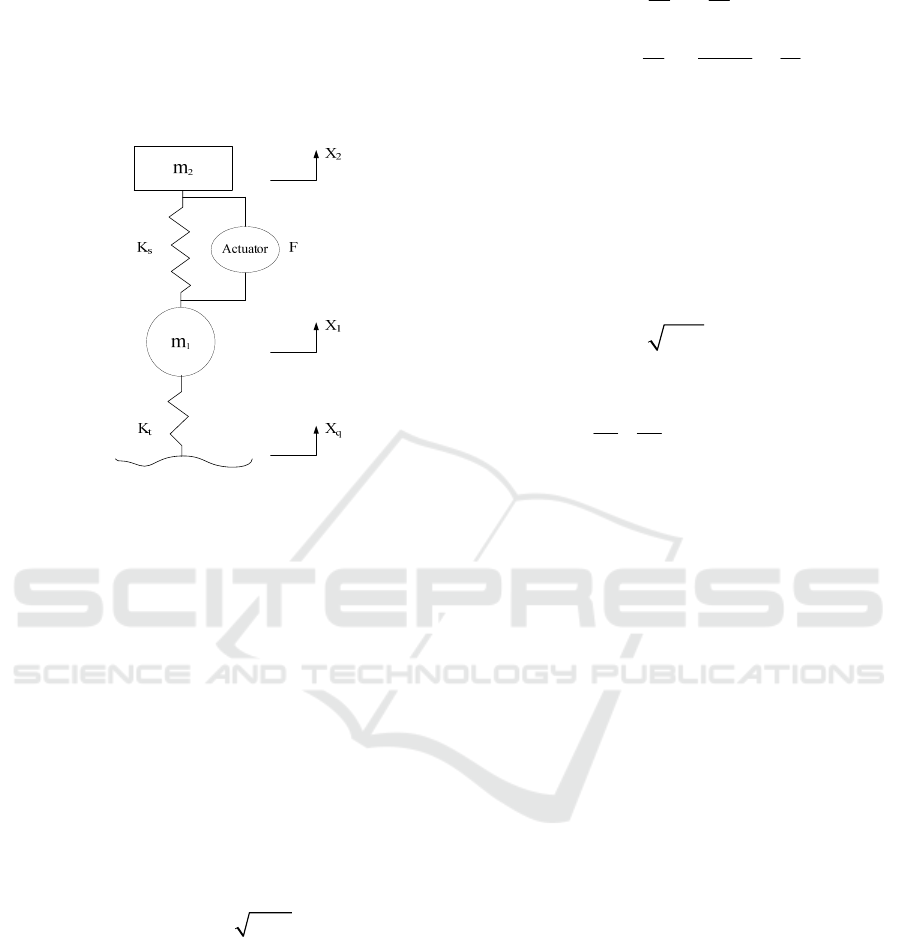
2 ESTABLISHMENT OF THE 1/4
ACTIVE SUSPENSION
CONTROL SYSTEM
For convenience, a simplified 1/4 vehicle model is
set up as research object, as figure 1 shows.
Figure 1:The quarter-vehicle body model of 2 DOEs.
In figure 1, the symbole k
t
is the tire stiffness,
and k
s
is the suspension stiffness. The symbol m
1
means the non-sprung mass and m
2
means the
sprung mass. And symbol F is the force of the
actuator, and X
q
is the road input. X
1
means the
displacement of the non-sprung mass and X
2
means
the travel of the sprung mass.
The system state variables and the output
variables are chosen respectively as shown in
formula (1)&(2).
2121
(,, ,,)
T
q
X xxxxx

(1)
22 11
(, , )
T
q
Yxxxxx

(2)
The control input is the active force F. And the
filtering white noise is used to simulate the real road
input as follows shown in formula (3),
00() 2 () 2 ()qq
x
tfxtGVt

  

(3)
In above formula, the symbol G
0
means the
pavement roughness coefficient (m
3
/cycle). The
symbol V is the vehicle speed. The

(t) represents
the Gaussian white noise with zero mathematical
expectation. The f
0
means the lower cut-off
frequency(Zhou, 2012).
Then the system state-space equation(4) can be
achieved as follows,



x=Ax+BU
y=Cx+DU

(4)
The symbol A,B,C,D are annotated as follows,
22
111
0
00 0
00
10 0 0 0
01 0 0 0
00 0 0 2
ss
stst
KK
mm
KKKK
mmm
f




























A
2
1
0
01/
01/
00
00
20
m
m
Gv



















B
22
00 0
00
()
00 1 1 0 00, [ ]
00 0 1 1 00
ss
KK
mm
t
F

















CDU
3 MODEL OF PID CONTROLLER
OPTIMIZED BY THE PSO
The main performance indexes for the vehicle
suspension design consist of three ones, which are
the body vertical vibration acceleration, the
suspension dynamic travel, and the dynamic load of
the tyre.
The body vertical vibration acceleration
represents the car ride. The suspension dynamic
travel represents the body posture and the
suspension structure. And the he dynamic load of
the tyre represents the tire grounding characteristic.
So, the three variables are selected as the aim of PID
controller.
3.1 Design of PID Controller for the
Suspension
PID controller is a linear one. It forms the control
deviation
()et according to the given value ()rt
and the actual output value
()ct , as following
formula (5) shows.
() () ()et rt ct


(5)
PID Control for the Vehicle Suspension Optimized by the PSO Algorithm
173

It combines the proportion, integration and
differential of the deviation
()et to form a control
variable, and controls the object.
The body vertical vibration acceleration, the
suspension dynamic travel, and the dynamic load of
the tire is the representative of the suspension
performance. Therefore, they can be set as the
control aims. The active force F of the PID
controller is shown as follows,
0
()
*() * () *
T
pi d
de t
FKet K etdtK
dt
 

(6)
Among them,
p
K means the proportional
coefficient,
i
K means the integral coefficient, and
d
K is the differential coefficient.
When PID controller is adopted, the three
coefficients play decisive roles in control effects. To
solve the problems in deciding the three ones, the
PSO algorithm is used.
3.2 Optimization Procedure of the PSO
Algorithm for the PID Controller
The PSO optimization algorithm is derived from
prey behavior of birds. Similar to the GA, the PSO
algorithm first initializes a swarm of particles. Every
particle represents a possible solution to the
optimizing problem, which has its own position and
speed. The target function value according to the
particle position coordinate is decided as the
particle’s fitness. On every iteration, each particle
memorizes and follows current optimal particle. It
renews itself by tracing two extremums. One is the
optimal solution pbest found by itself, and the other
is the optimal solution found by the whole swarm
gbest.
After finding the two optimal values, the
particles renew their own speeds and positions
according to relative formula. And then the
unknown parameters,
p
K
,
i
K
and
d
K
, can find their
optimal solutions from the assembly of all possible
values by the PSO algorithm. And the fitness
function value is the minimum(Wang, 2011; Yan,
2011).
The optimization procedure of the PSO
algorithm for the PID controller is shown as figure
2.
Figure 2: Optimization process of PID controller by PSO
algorithm.
1
）
Renewing of Particle swarm
Since the parameters can not deal with the space
parameters directly, the feasible solution must be
coded as the particle space unit. And the PID
parameters code are the particle code cluster, which
is the matrix [
p
K
,
i
K
,
d
K
]. Every variable of the
particles is expressed by real number and its value
range is decided by specific application background.
And then the PSO algorithm is used to search the
optimal solutions of above variables. By preliminary
setting, the range of the three PID parameters is set
to [0, 50].
2
）
Each particle are evaluated to the three
parameters successively, and then the active force F
of the PID controller is solved and sent to the 1/4
body model.
3
）
Fitness function values of every swarm are
solved.
Because of the magnitude order of the
performance indexes, which are
3
x

,
（
32
x
x
）
and
1
()
q
x
x

, the fitness function value L is set as
follows.
ICECTT 2018 - 3rd International Conference on Electromechanical Control Technology and Transportation
174

3
3
32
32
1
1
[()]
Minimum L
[()]
[( )( )]
[( ) ( )]
[( )( )]
[( ) ( )]
pass
pass
q
qpass
RMS x
RMS x
RMS x x
RMS x x
RMS x x
RMS x x







X
X
X
X
X
X


(,, )Kp Ki KdX
，
1<Xi<50
，
i=1,2,3
3
3
32
32
1
1
[()]
1
[()]
[( )( )]
.. 1 (7)
[( ) ( )]
[( )( )]
1
[( ) ( )]
pass
pass
q
q pass
RMS x
RMS x
RMS x x
st
RMS x x
RMS x x
RMS x x


















X
X
X
X
X
X


Among the formula, RMS means the mean
square root of the relative data.
3 pass
x

means
vertical acceleration of passive
suspension.
32
()
pass
xx
means the dynamic travel
of passive suspension.
1
()
q pass
xx
means the
dynamic displacement of the tire. And X is the PID
coefficient matrix.
Fitness function value can be calculated by
formula (6) and it is the termination condition for
the PSO algorithm. If condition is satisfied, the
algorithm will end. If not satisfied, the previous step
continues to change the PID parameters.
4
）
Renewing of the position and speed of the
particle.
For every particle, its fitness value is compared
to its optimal position-fitness value and whole
particles’ optimal position-fitness value. If better, the
value is set as current optimal position, and the
particle’s speed and position is renewed.
And the speed and position is decided by
following formula (8).
111 22
11
()( )
t t tt tt
ttt
vvcrPxcrGx
xxv



  




(8)
Among the formula,
x
means the particle’s
position.
v
means the particle’s speed.

means
the inertia factor.
1
c
、
2
c
mean acceleration const.
1
r
、
2
r
are random numbers among [0,1].
t
P
is the
optimal position-fitness value of the particle. And
t
G
is the optimal position-fitness value of all
particles.
5
）
If the termination condition is not satisfied, the
procedure returns to step 2), or the optimal solution
is achieved.
3.3 PID-control Model for Suspension
under Matlab/Simulink
Circumstance
The PID-control model for active suspension is
realized under Matlab/Simulink circumstance, as
figure 3 shows. The input signal is the road stimulus.
The output signals are the vertical acceleration,
vertical body speed, the travel of suspension and the
displacement of the tire.
Fig.3 PID controller model for active suspension in
simulink
The vertical body speed is selected as the input
variable for the PID controller. And the output of the
PID controller acts as the active force of the
suspension. The suspension output is selected as the
input variables for the fitness function value of the
PSO.
4 SIMULATION EXPERIMENT
AND RESULT ANALYSIS
The initial condition for PSO algorithm is set as
follows.
The ranges of the three parameters,
p
K
,
i
K
and
d
K
, are all set in[1,50]. And their deviations
are 1×10-6.
The road input model uses the filtered white
PID Control for the Vehicle Suspension Optimized by the PSO Algorithm
175

noise, and made by the WGN
（
M, N, P
）
function of
MATLAB. M and N are the rows and columns of the
generative matrix. And P is the power of the filtered
white noise
（
dB. M, N and P are set to 10001, 1 and
20 accordingly. The sampling time is 0.005s, and the
vehicle speed is 20m/s. And the total simulation time
is 50 seconds.
The vehicle parameters are set as follows.
m
2
=300kg. m
1
=50kg. k
s
=20000N/m. k
t
=200000 N/m.
The operation distance of the suspension is ±
100mm.
After optimization, the three parameters,
p
K
,
i
K
and
d
K
are 11.3617, 0.01 and 49.05.
The simulation results are shown as figure 4-6.
Figure 4: Vertical accelerations of active and passive
suspension.
Figure5: Working distances of active and passive
suspension.
Figure 6: Wheel dynamic travels of active and passive
suspension.
Among the figures, the red line represents the
passive suspension, and the black line represents the
active suspension. To confirm the advantage of the
PSO algorithm in optimizing the PID controller
(PSO-PID), the control performances of the active
suspension are compared to the passive one. The
analysis result is shown on table 1.
Table 1: Performance indexes of suspension controlled by
different manners.
Performance
indexes
unit
Root mean square value (RMS)
Passive
suspensio
n
Active
suspensio
n by
normal
PID
controlle
r
PSO
-PID
Vertical
acceleration
m/s
-2
5.2716 4.5 3.954
dynamic
travel of
suspension
mm 3.135 2.986 2.467
dynamic
displacemen
t
of the tyre
mm 0.2190 0.310 0.231
From fig4~6 and table 1, we can see that the
suspension performance indexes, especially the
suspension dynamic travel and vertical acceleration,
are dramatically improved when PSO-PID is used.
This means that, the PSO algorithm has a great
application effective when used in suspension
control. Though the index, dynamic displacement of
the tyre, is no better than other control manners, it
has no big influence on the suspension performance.
5 CONCLUSIONS
This paper used the global-searching ability of the
PSO algorithm to optimize the three parameters of
ICECTT 2018 - 3rd International Conference on Electromechanical Control Technology and Transportation
176

the PID controller in suspension control. The design
efficiency and control performance of the PID
controller are greatly improved. The advantages can
be expressed in two respects.
1）The problems in deciding the three parameters
of the PID controller are well solved. Thus the
deciding efficiency and control performance are
bettered.
2）The three performance indexes of the vehicle
suspension are improved.
ACKNOWLEDGMENTS
The authors gratefully acknowledge the financial
support from the National Natural Science
Foundation of China and the Natural Science
Foundation of Jiangsu province.
REFERENCES
H.Zhang,Y.Shi,Junmin Wang(2013), Observer-based
tracking controller design for networked predictive
control systems with uncertain Markov delays,
International Journal of Control,86,10, 1824-1836.
Y.G. Zhao,J.Chen(2011),Co-simulation on semi-active
suspension of Vehicles, Noise and vibration
control(China),31,5,104-107.
H.Zhang, Junmin Wang, Y.Shi(2013), Robust H∞
sliding-mode control for Markovian jump systems
subject to intermittent observations and partially
known transition probabilities, Systems & Control
Letters,62,12,1114-1124.
L.J.Chai,C.Sun,J.Z.Feng ( 2010),Design of the LQG
Controller for Active Suspension System Based on
Analytic Hierarchy Process, Automotive
engineering,32,8,712-718.
D.Liu,Y.Tang,H.Y.Gu(2010). The development of
automotive active suspension control system,
Hydraulics Pneumatics & Seals,5,4,21-25.
J.W.Wang,J.M.Zhang(2006),Multi-objective Optimization
Design of Gear Reducer Based on Simulated
Annealing Algorithms [J]．Transactions of the Chinese
society for agriculture machinery,37,10,120-123．
Zhou Rou ， Guo Zhifeng. Research on active
suspension control technology[J].Journal of Tongji
university..2012，197：176-180.
L.Wang(2011), The intelligence algorithm and its
application, Tsinghua University press,105-108．
Annealing Algorithms [J]．Transactions of the Chinese
society for agriculture machinery,37,10,120-123．
W.J.Yan,D.Dong, W.R.Wang(2011). On fuzzy strategy
of nonlinear semi-active suspension system, Control
engineering of China, 18,6,941-946.
PID Control for the Vehicle Suspension Optimized by the PSO Algorithm
177