
A Phase-Locked Loop Clock Synchronization Method Combined with
Discrete Spectrum Correction
Yueqin Wu, Xiaoquan Xu, Kuan Li, Youmei Hu and Kun Han
Institution of Pattern Recognition and Application, College of Automation, Chongqing University of Posts and
Telecommunications, Chongqing 400065, China
E-mail:2722794314@qq.com
Keywords: Wireless sensor networks, Clock synchronization, Signal process, Phase-locked loop,Physical layer.
Abstract: The main purpose of this paper is to achieve clock synchronization between physical layers of network nodes,
and to achieve frequency synchronization and full synchronization by exchanging clock information through
pulse-coupled discrete time phase-locked loop. This article is mainly to use the discrete spectrum correction
method to reduce the influence of noise caused by crystal oscillator clock signal in transmission process due to
various reasons, then establish Laplacian matrix which consist of relative signal intensity of nodes to control
the update amount of clock information, finally the synchronization steady state between network nodes is
achieved.
1 INTRODUCTION
Wireless sensor network (WSN) is a large-scale,
self-organizing and multi-hop distributed sensor
network which can achieve data acquisition,
processing and transmission. It consists of many
sensor nodes and each node is timed by a local clock
module which is usually provided by a crystal
oscillator. Due to the independence, physical
dispersion of node, the error of crystal frequency is
to be different, then the local clock between nodes
are asynchronous that affect the data processing. So
there are many time synchronization technologies.
Time synchronization determines the service quality
of wireless sensor network, and it is important to
improve the quality and efficiency of people's life.
Time synchronization technology has been a
focus in wireless communication field. Many kinds
of time synchronization algorithms have been
studied to reduce power consumption, complexity,
and improve accuracy. The common network time
synchronization (NTP) in computer is to
synchronize the clock to world coordination time
UTC, which can provide high precision of time
correction. NTP propagate (Mills D. 1992)
according to the rank of server, and the hierarchical
structure is divided according to the distance, but it
can’t meet the requirements of low power
consumption, limited bandwidth and wireless
transmission, so it’s not suitable for wireless sensor
networks. The traditional time synchronization
protocol has reference broadcast synchronization
mechanism (RBS) based on receiving to receiving
mode, the delay measurement time synchronization
DMTS (Ping S. 2003) based on sending to receiving
unidirectional mode, the TPSN based on sending to
receiving bi-directional mode. A new time
synchronization technology is firefly
synchronization (Hailei Zhao. 2015). The interaction
between fireflies is modeled as electric coupling.
The coupling start and it changes the state quantity,
while the state variable changes the phase quantity.
The phase difference is reduced by synchronization
process, finally caused the full synchronization.
Synchronization can be done directly in the physical
layer without the need for message transmission and
the synchronization accuracy is not affected by
MAC delay, protocol processing, etc.
Therefore, this paper analyzes the frequency and
phase synchronization as clock synchronization on
the basis of physical layer. Because in the
transmission process, the signal of crystal oscillator
will cause noise due to various factors, so we use the
signal processing method of asymmetric window in
discrete spectrum to reduce the influence of noise on
signal. Then a discrete time clock model is
established. Due to the information exchange by
coupling clock, the update of node clock is link with
other nodes in network. According to the network
228
Wu, Y., Xu, X., Li, K., Hu, Y. and Han, K.
A Phase-Locked Loop Clock Synchronization Method Combined with Discrete Spectrum Correction.
In 3rd International Conference on Electromechanical Control Technology and Transportation (ICECTT 2018), pages 228-231
ISBN: 978-989-758-312-4
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

topology, the relative signal strength between nodes
is defined, and then established Laplacian matrix to
control update of node clock, finally realize the
stable synchronous state.
2 DISCRETE SPECTRUM SIGNAL
PROCESSING
The clock node in network is a time measuring
device which composed of an oscillator and a
battery. Due to various reasons in transmission
process, the discrete time clock affected by noise, so
this paper choose signal processing method of
asymmetric window correction(MBAW) to process
noise. The asymmetric window is built by cutting
the symmetric window with a straight line which
used the original point. It can get some properties of
asymmetric window through simulation comparison
between asymmetric window and corresponding
symmetric window. For simplify the description of
asymmetric window function, it use A- Hanning
window to show asymmetric hanning window in
fig.1, fig.2 and fig.3 is similar.
From fig.1, fig.2, fig.3, It can be concluded that
asymmetric and symmetric window with the same
amplitude characteristics, the attenuation rate of side
lobe envelope is almost agreement, and phase line of
symmetrical window and corresponding asymmetric
window is always intersect in center of main valve
which lays the theoretical foundation for the
asymmetric window phase difference algorithm.
0 20 40 60 80 100 120 140
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
samples
Am plitude
Symmetri c
Asymmetri c
0 2 4 6 8 10 12 14 16
-100
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
frequency
M agnitude
Symmetric
Asymmetric
-1 -0.5 0 0.5 1 1.5 2
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
Frequency
phase
Symmetri c
Asymmetri c
Figure 1: Hanning window and A-hanning windonw.
Figure 2: Blackman window and A-blackman window.
0 20 40 60 80 10 0 120 140
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
simple
Am plitude
Symmetric
Asymmetric
0 2 4 6 8 10 12 14 16
-100
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
fr equency
Magnitude
Sy mmetr i c
Asy mme tri c
-1 -0.5 0 0.5 1 1.5 2
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
Freq uency
phase
Symmetric
Asymmetric
Figure 3: Kaiser-bessel window and A-kaiser-bessel
window.
It’s assumed that cosine signal is
(t)=Acos(2
+) and the function of window is
, the normalized phase can be obtained by DFT.
Two different window functions are added to the
same signal (one is symmetric one is asymmetrical),
then it can get two different phase values
∅
(1)
∅
(2)
Where denotes the frequency bin number in
the discrete spectrum and
∆
⁄
,
∆
is
frequency resolution. Let (2) subtract (1), the phase
difference can get
∆∅
∅
∅
(3)
Because the phase line of asymmetric window
and symmetric window always intersect at the center
of main lobe, so there is u
0 when
,
that is, the value of normalized frequency is the
solution of equation u
0, and the solution of
this equation can be approximately obtained by
secant method.
3 DISCRETE TIME CLOCK
SYNCHRONIZATION
After noise processing, the discrete time clock
0 20 40 60 80 100 120 140
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
samples
Am plitude
Symmetric
Asymmetric
0 2 4 6 8 10 12 14 16
-100
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
fr equency
Magnitude
Symmetric
Asymmetric
-1 -0.5 0 0.5 1 1.5 2
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
Frequency
phase
Symmetric
Asymmetric
A Phase-Locked Loop Clock Synchronization Method Combined with Discrete Spectrum Correction
229
model can be approximated as a non-noise state
0
(4)
Where
denotes the time of the th
tick(=0,1,2…)of the th clock(=1,2,…,N, where
N is the total number of nodes),
is the local
periods.
Because of the network topology, the impact of
each node on local nodes is different. Therefore, it
defined that
is the relative strength of the signal
received by from with respect to the other
neighbors of (there is a normalization
condition
∑
=1), and Laplacian matrix can be
established according to the connection state of
nodes.
=
∑
∈
(5)
A
(6)
Where
indicates the power received from
the node to the node, A is an adjacency matrix
(
=
for and
=0), so we have ∙
0, where 1=[1 1 … 1]
T
.
Pass through time difference detector of the
phase-locked loop, the time information that the
local clock node needs to be coupled can be
obtained.
∆
∑
,
∙
(7)
Then the clock information of the node is
updated by the first order loop filter
1
∙
∑
∙
,
(8)
And the clock information controlled by the
Laplacian matrix can be obtained by converting (8)
into a vector difference equation.
t
1
∙
(9)
Where the vectors
⋯
,
⋯
. Let
is the common frequency, so there is
t
0
∙
∙
∙
(10)
Plugging (10) in (9), we can get
1
∆
∙
(11)
Where ∆=
∙, so in the steady-state,
there is
1
=0, then obtaining the
condition
∙
∆
(12)
There is
0,
⋯
is the left
eigenvector corresponding to λ
0. Then the
value of common frequency easily follows:
(13)
Moreover, through the further change of
variables
1
∆
in (11),we
obtain
1
. since
1
→1
1
,which finally leads to (14)
t
→
∙∙
0
∆
∆
(14)
Finally the neighbor nodes are synchronized, and
the system reaches a stable state.
4NUMERICAL SIMULATIONS
The theoretical signal which is worsened by noise is
,e
is the white noise with
zero mean and gauss distribution. It can get the
signal to noise ratio (SNR) from -5 to 90 dB through
adjusting noise level, the theoretical frequency is set
to 256Hz, the sampling frequency is 1024Hz,
sample point is 1024 and the phase is π. Because
of the randomness of noise, the frequency correction
results are different in each test, so the root mean
square error of the 500 independent experiments is
considered.
RMSE
∑
(15)
Where
is test number,
is the correction
frequency of each test in the case of noise.
-0.5 -0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4 0.5
10
-10
the normalized frequency deviation
frequency error[Bin
]
mbts
mbtwc
interpolation
mbaw
-0.5 -0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4 0.5
10
-10
10
0
the normalized frequency deviation
Phase error
mbts
mbtwc
interpolation
mbaw
-0.5 -0.4 -0.3 -0.2 -0.1 0 0.1 0.2 0.3 0.4 0.5
10
-10
the normalized frequency deviation
Amplitude error
mbts
mbtwc
interpolation
mbaw
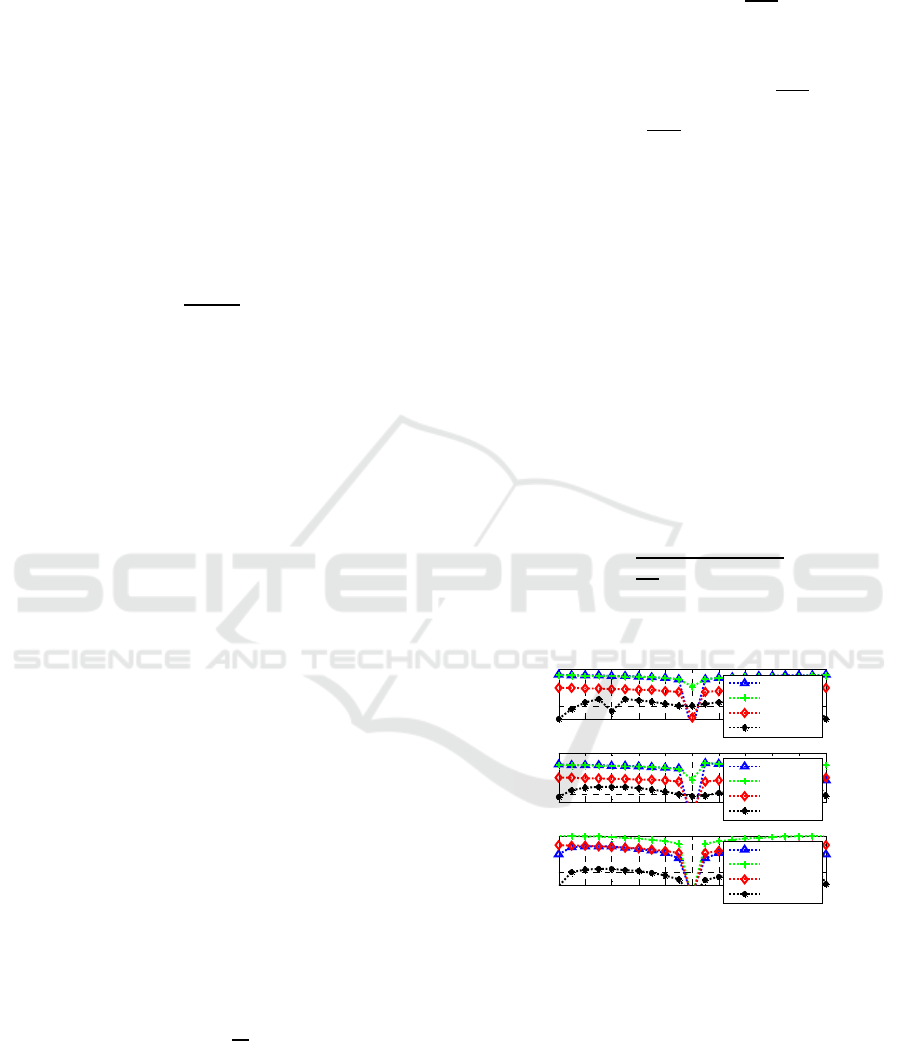
Figure 4: Maximum frequency, phase and amplitude errors
for different algorithms.
ICECTT 2018 - 3rd International Conference on Electromechanical Control Technology and Transportation
230
-10 0 10 20 30 40 50 60 70 80 90
10
-7
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
SNR[db]
RMSE
mbts
mbtwc
interpolation
mbaw
Figure 5: RMSE of 500 independent trials.
From fig.4 and fig.5, it can be seen that the
signal processing method of asymmetric window
makes the frequency, phase and amplitude errors
small enough, and with the increase of SNR, the
RMSE gradually decreases, which can reduce the
influence of noise.
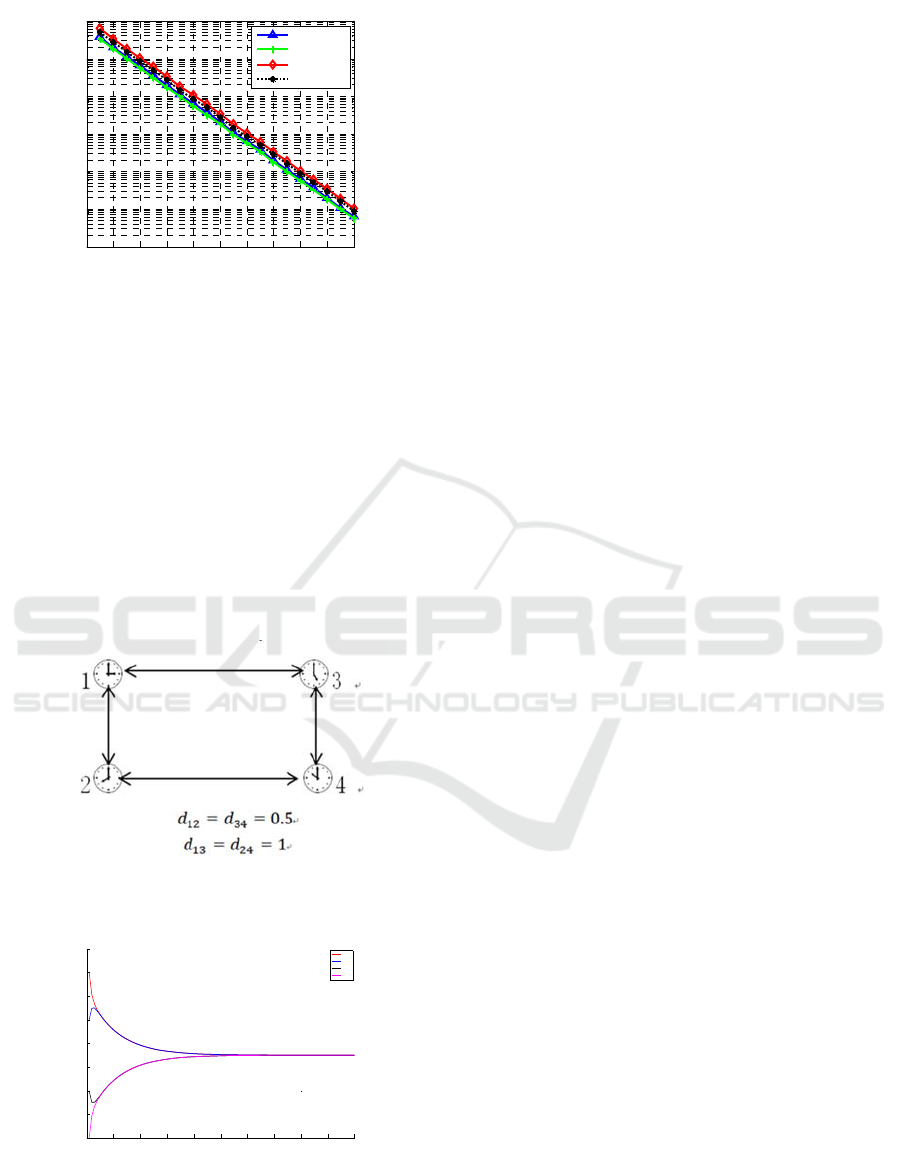
Here it consider a simple example for N=4,
1
⁄
, the common frequency T
=1,
=0.4, t
0
0.90.70.40.2
.From fig.7. it can
be seen that as long as there is a path connection
between nodes, the nodes can achieve phase
synchronization so that achieve full synchronization
and
converge to
∑
0
.
Figure 6: Connection diagram of Network node for N=4
Figure 7: Phases of the N=4 pulse-coupled discrete clocks
shown in the box versus period n
5 CONCLUSIONS
This paper proves that combined with the correction
of discrete spectrum, the influence of noise in
network node's clock can be reduced, and the stable
synchronization between nodes clock can be
achieved by pulse coupling in physical. The left
eigenvector of the Laplacian matrix yields the steady
state frequency and phase of the clock.
REFERENCES
Simeone O, Spagnolini U, Bar-Ness Y, et al. 2008.
Distributed synchronization in wireless networks[J].
Signal Processing Magazine IEEE, 25(5):81-97.
Luo J, Xie M. 2015. Phase difference methods based on
asymmetric windows[J]. Mechanical Systems & Signal
Processing, 54-55:52-67.
Ping S. 2003. Delay Measurement Time Synchronization
for Wireless Sensor Networks[J]. IRB.
Ganeriwal S, Kumar R, Srivastava M B. 2004.
Timing-sync protocol for sensor networks[C].
International Conference on Embedded Networked
Sensor Systems. ACM, 138-149.
Sichitiu M L, Veerarittiphan C. 2003. Simple, accurate
time synchronization for wireless sensor networks[C].
Wireless Communications and Networking, 2003.
WCNC 2003. IEEE, 1266-1273 vol.2.
Mills D. 1992. Network Time Protocol (Version 3)
Specification, Implementation[J]. Rfc.
Hailei Zhao. 2015. Research on distributed time
synchronization technology of wireless sensor network
based on "firefly synchronization" [D]. Beijing
Institute of Technology.
Kang D, Jiang L. 2001. Energy Centrobaric Correction
Method for Discrete Spectrum[J]. Zhendong
Gongcheng Xuebao/journal of Vibration Engineering,
14(3):354-358.
Luna A, Rocabert J, Candela J I, et al. 2015. Grid Voltage
Synchronization for Distributed Generation Systems
Under Grid Fault Conditions[J]. Industry Applications
IEEE Transactions on, 51(4):1-1.
Su S, Lin Z, Garcia A. 2015. Distributed Synchronization
Control of Multiagent Systems With Unknown
Nonlinearities[J]. Cybernetics IEEE Transactions on,
46(1):1-1.
Narduzzi C, Offelli C. 1987. Real-time high accuracy
measurement of multifrequency waveforms[J]. IEEE
Transactions on Instrumentation & Measurement,
IM-36(4):964-970.
Andria G, Savino M, Trotta A. 1989. Windows and
interpolation algorithms to improve electrical
measurement accuracy[J]. IEEE Transactions on
Instrumentation & Measurement, 38(4):856-863.
0 10 20 30 40 50 60 70 80 90 100
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1
4
4
P
i=1
t
i
(0)
t
1
(n)-nT
t
2
(n)-nT
t
3
(n)-nT
t
4
(n)-nT
A Phase-Locked Loop Clock Synchronization Method Combined with Discrete Spectrum Correction
231
