A Scheduling Strategy in Fusion Estimation with Bandwidth
Constrained
Kuan Li, Yueqin Wu, Xiaoquan Xu, Youmei Hu and Kun Han
Institute of detection technology and smart sensing,Chongqing University of Posts and Telecommunications,Chongqing
Keywords: Scheduling Strategy, Multi-Sensor Fusion, Bandwidth Constrained.
Abstract: This paper presents a sensor scheduling strategy for multi-sensor fusion estimation system to meet the
bandwidth constrained. First the sensors are divided into several groups. Then the local optimal estimation
of each subsystem is transmitted periodically. By reducing the transmission of information at a time, it not
only meets the limitation of communication bandwidth, but also saves the energy of sensor nodes and
prolongs the lifetime of network. The kalman fusion estimator,which is suitable for this scheduling strategy
is redesigned to get the option fusion estimation. Finally, a simulation of target tracking is used to illustrate
the effectiveness of the proposed sensor scheduling strategy.
1 INTRODUCTION
The purpose of the multi-sensor fusion estimation
system is to cooperatively perceive, collect the
information of the perceived objects and then send
them to the fusion estimation center,which can
accurately extract the information of the detection
objects through the fusion estimation center(
You K
and Xie L, 2011). The introduction of wireless
communication network brings mobility and
flexibility to the original communication network,
and reduces the cost of networking, but also brings
many new challenges. Among them, the wireless
communication network constraints. For this
problem, researchers have done a great deal of
research work and achieved a lot of achievements.
However, there are still many problems to be further
study. The current methods to solve the problem of
bandwidth limitation can generally be divided into
three types, quantizing(
Sani and Vosoughi, 2016; Liu
and Xu, 2014; Li and Alregib, 2009), dimensionality
reduction(
Schizas and Giannakis, 2007; Zhu and Schizas,
2009
)and sensing scheduling(Han and Mo, 2014;Han
and Mo, 2016
).
An adaptive quantitative strategy is presented to
design a distributed estimator to meet the constraints
of bandwidth limitation(Liu and Xu, 2014; Li and
Alregib, 2009). Schizas and Zhu discussed how to
design the dimension compression algorithm, and
gave the proof of the existence of the optimal
compression matrix under the linear minimum
variance optimization criterion.(Schizas and
Giannakis, 2007; Zhu and Schizas, 2009). The
channel is divided into high-precision channel and
low-precision channel. Reducing energy
consumption and evaluating performance are both
took into consideration, then the opportunistic
sensing scheduling with high accuracy and low
accuracy was proposed. All of the above two
methods were in the perspective of data transmission
to consider the issue(Han and Mo, 2014;Han and Mo,
2016).
Because of limited communication resources,
multiple sensors share wireless channels. If all
sensors send data at the same time, it is easy to get
blocked and lose packets.In this paper, we presents a
sensor scheduling strategy to meet the bandwidth
constraints. Firstly, the sensor in the whole system is
divided into several discrete subsystems. Subsystems
transfer the optimal local estimate in the sense of
linear minimum variance to the fusion estimation
center. The fusion center estimates performance
based on the optimal matrix-weighted fusion
criterion. Finally, an simulation of fusion estimation
algorithm is used to verify the effectiveness of
sensor scheduling strategy that we proposed in the
fusion estimation.
236
Li, K., Wu, Y., Xu, X., Hu, Y. and Han, K.
A Scheduling Strategy in Fusion Estimation with Bandwidth Constrained.
In 3rd International Conference on Electromechanical Control Technology and Transportation (ICECTT 2018), pages 236-240
ISBN: 978-989-758-312-4
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

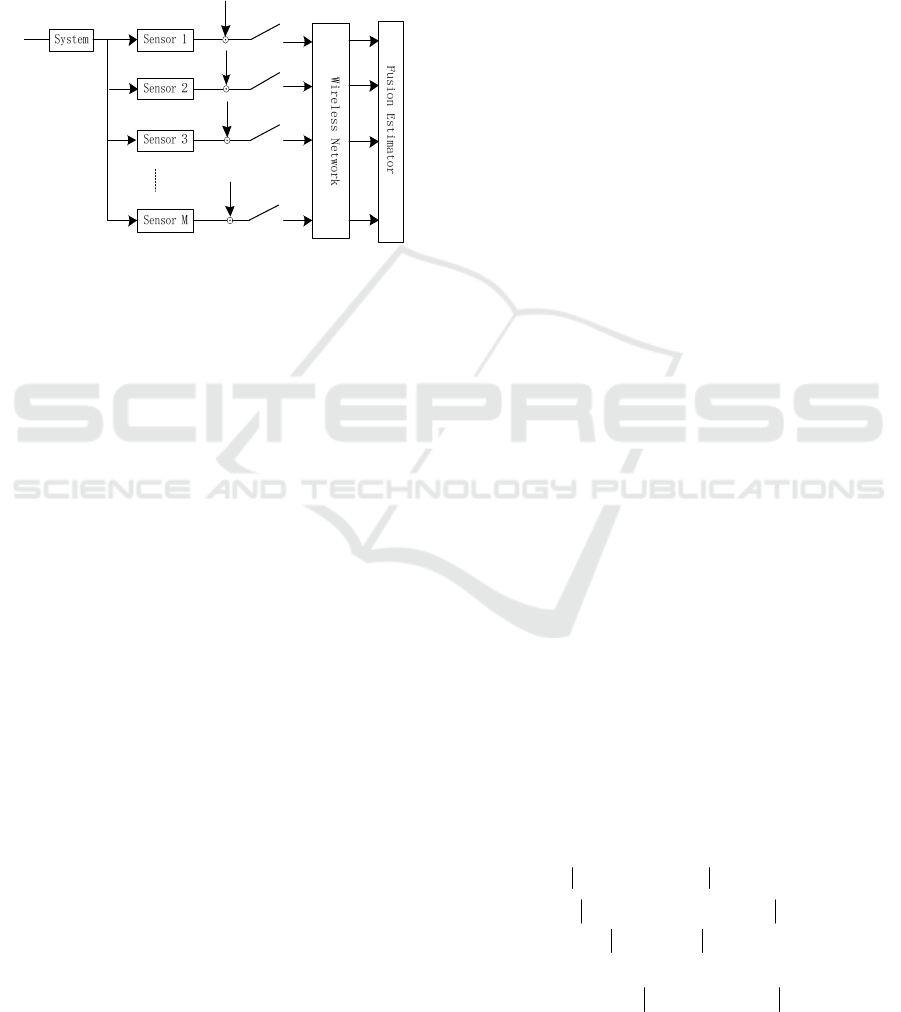
2 PROBLEM DESCRIPTION AND
SCHEDULING STRATEGY
2.1 Dynamic physical processes
In this paper, we consider the multi-sensor
information fusion problem with bandwidth
constrained, as shown in figure 1.
k
w
k
x
1 k
cx
2 k
cx
3 k
cx
N
k
cx
(1)
k
v
(2)
k
v
(3)
k
v
()
k
vM
(1)
k
y
(2)
k
y
(3)
k
y
()
k
yM
Figure 1. Multi-Sensor Fusion System Structure
The discrete time invariant system model is as
follows:
(1) () ()
x
kAxkBwk+= + (1)
() () (), 1,2,...,
ii i
yk Cxk vki m=+= (2)
where
()
n
x
kR∈
and
()
i
m
i
y
kR∈ represent system
state and measurement output of
ith sensor
respectively.
,,
i
A
BC are the coefficient matrix of
the appropriate dimensions.
()
n
wk R∈ and ()
i
m
i
vk R∈ are uncorrelated Gaussian
white noises with mean zero and covariance
,
i
v
QR
.
Assuming the initial value of system state
is
0
(0)
x
x= ,where
0
x
is a gaussian random variable
with mean
0
μ
.
2.2 Scheduling Strategy
For the system shown in the figure 1, there
are
m sensors that need to send the measurement
information over the wireless network to the fusion
estimation center node. Due to the bandwidth
limitation, only
a sensors are allowed to send their
own measurement data. we named the
m sensors as
12
, ,...,
m
s
ss. Then the m sensors according to the
principle of proximity is divided into
N groups
and the number of sensors in each group is less than
or equal to
a
. The sensors set is defined
as
1
{ ,... ,..., }
im
s
ss s=
and the group set
is
12Δ ()
ˆ
{ ,..., ,..., }ss s s=
h
hh h h
where {1, 2,... }N=h .
According to the above transmission strategy, we can
know that
s
and
ˆ
s
h
are satisfied:
12
1
ˆˆ
ˆ
ˆˆ
... , ( )
ˆ
Δ() , ( )
Ni j
N
s
ss sss ij
mnumbers a
=
=∪ ∪ ∩ =∅≠
==
∑
h
h
h
(3)
where ()number A is the number of elements in
set
A
. In this way, only one group of sensors in the
ˆ
s
h
set is allowed to send measurement data in each
sampling period. The fusion center has all the
measurement information from
(1)kN th−+
sampling period to the
kth
sampling
period of all this group sensors. For example, there
are four sensors in this system, and the number of
sensors which allowed to send data is two. It means
4, 2sa==
. The sensors node set is
1234
{, , , }
s
ssss= .
We divided the sensors in two
groups.
1122 34
ˆ
ˆ
2, { , }, { , }Nssssss== =
.The
measurement data of the sensors in
1
ˆ
s
is transmitted to
the fusion center when
1,3,5,...k =
. The
measurement data of the sensors in
2
ˆ
s
is transmitted to
the fusion center when
2, 4, 6,...k =
.
2.3 problem description
The problem we hope to solve is to design a
distributed kalman fusion estimator that satisfies the
constraint equation (4) based on the above
transmission strategy.
*
**
ˆ
()
ˆˆ
argmin {( () ()) ( () ())}
T
xt
Ext xt xt xt−−
(4)
3 DESIGN OF DISTRIBUTED
KALMAN FUSION ESTIMATOR
The optimal estimator
ˆ
x
h
in the sense of the linear
minimum variance of the
ith
subsystem can be
calculated based on the kalman filter(Deng and
Gao,2005):
1
ˆˆ
() [ ] ( 1) () ()
(1)()[(1)() ]
rr
n
rT r rT
x
kICAxk Kkyk
Pkk C CPkk C R
−
⎧
=− −+
⎪
⎨
−−+
⎪
⎩
hhhhh
hhhhhh
(5)
()[ ()]( 1)
(1) ()
r
n
TT
Pkk I K kC Pkk
Pk k APkkA BQB
⎧
=− −
⎪
⎨
+= +
⎪
⎩
hhhh
hh
(6)
The forecast of the
t
steps ahead is:
1
ˆˆ
() (1)
t
x
ktk Axk k
−
+= +
hh
(7)
The covariance matrix is:
A Scheduling Strategy in Fusion Estimation with Bandwidth Constrained
237

11
2
ˆ
(){(()())
ˆ
(( ) ( ))}
()()
()
T
ttT
t
tj T tjT
j
Pk tk E x k t x k tk
xk t xk tk
APktkA
ABQBA
−−
−−
=
+= +− +
+− +
=+
+
∑
hhh
hh
h
(8)
According to [9], we can define that:
10
00
ˆ
()[ () ()],=[ ]
ˆ
ˆ
ˆ
( ) {( () ())( () ())}
TTT T
aLnn
aa
x
tt x tt x tt I I I
Ptt E Ixt x t Ixt x t
⎧
=
⎪
⎨
=− −
⎪
⎩
LL
(9)
The optimal distributed kalman fusion estimator
in the sense of linear minimum variance is as
follows(Sun and Deng, 2004):
1
ˆ
ˆ
() ()()
L
oii
i
x
tt F t x tt
=
=
∑
(10)
For the fusion estimator, the minimum
covariance matrix of the fusion error
is:
ˆˆ
() {[() ()][() ()]}
T
ooo
Ptt E xt x tt xt x tt=− −
11
00
ˆ
()( ())
T
o
Ptt IP ttI
−−
= (11)
The optimal weight matrix can be calculated by
(12).
111
12 0 00
ˆˆ
[ ( ), ( ),..., ( )] ( ( ) ) ( )
TT
L
F
tFt Ft IP ttI IP tt
−−−
=
(12)
Lemma1:Define
ˆ
()( )()
ii i
x
ktk xktkt xktk+= ++− +
%
.
The error covariance matrix of
ith group sensors
and
jth group sensors (, )
ij
Pkkk t− is computed by
the following recursive equation.
1
0
1
(, ) {(()( )}
Π [( ( ) ) ]
[( 1)]()
T
ij i j
t
r
ii
j
rjT
ii
Pkkk t E xkkx kk t
IKkrCA
I
Kk j C BQA B
−
=
−
−= −
⎛⎞
=−−
⎜⎟
⎝⎠
×− −+
%%
(13)
Lemma 2
：The error covariance matrix of
1
tthstep
forecast of
ith group sensors and
2
tth step forecast of ith group
sensors
12
(,)
ij
Pkk tk t−− is computed by the
following recursive equation.
11
1
12 1 2
11 2
11
1
(,){(()()}
(,)()
()
T
ij i j
tt
T
ij
t
jjT
j
P
kktkt Exkktxkkt
APktktkt A
ABQAB
−−
=
−−= − −
=−−−
+
∑
%%
(14)
Proof:The proof of Lemma1 and Lemma 2 are
omitted due to page limitation.
Based on the above statement, the computation
procedures for the fusion estimator with bandwidth
constraints can be summarized as follows:
Algorithm I
：
1、Divided the sensors into N groups.The groups
are then numbered, which provides for the
periodic sending of sensor information .
2
、 Given the initial value (0 0)
i
P , (0 0)
ij
P ,
(0)P ,
ˆ
(0)
x
.
3
、Calculate the local optimal estimation
ˆ
()
x
k
h
of each sensor separately
， Based on
standard kalman filtering and(5-7)
calculate remaining groups’ optimal
estimate
ˆ
(1)
xkk N−+
h
.
4
、Calculate
ii
P by(6-8),and
ij
P by(13-14).
5
、The result of the fourth step is brought into
(12) to get the optimal fusion estimate.
6
、 Return to the third step and continue to
calculate the optimal fusion estimate for the
next moment.
4 SIMULATION
This simulation considers a goal of variable speed
motion and use four sensors for target
tracking.
() [ () () ()]
T
x
tststst=
&&&
. According to the
proposed sensor packet transmission strategy, the
sensor nodes are divided into two
groups,
1122 34
ˆ
ˆ
{, }, {, }
s
ss s ss==.The information
transmitted to the fusion estimation center is
estimated according to a fusion estimation
algorithm.The discrete time invariant system model
is (1) and (2).
Where:
22
12 34
10.5
10
01 , ,= ==
01
00 1 1
TT T
ATBTCCCC
⎡⎤⎡⎤
⎡⎤
⎢⎥⎢⎥
== =
⎢⎥
⎢⎥⎢⎥
⎣⎦
⎢⎥⎢⎥
⎣⎦⎣⎦
()
i
vt and ()( )
j
vti j≠ are uncorrelated
noise.
1Q = .The covariance of the sensors are:
123
0.9 0 0.3 0 0.6 0
,,
0 0.5 0 0.8 0 0.4
vv v
RRR
⎡
⎤⎡ ⎤⎡ ⎤
===
⎢
⎥⎢ ⎥⎢ ⎥
⎣
⎦⎣ ⎦⎣ ⎦
,
4
0.7 0
00.2
v
R
⎡
⎤
=
⎢
⎥
⎣
⎦
. The sampling period is 1T = .
According to the initialization parameters given
above, combined with the second part of the
distributed kalman fusion estimation algorithm can
get the target state trajectory curve.As shown below.
ICECTT 2018 - 3rd International Conference on Electromechanical Control Technology and Transportation
238

0 5 10 15 20 25 30 35 40 45 50
-1400
-1200
-1000
-800
-600
-400
-200
0
200
Tim e s /s
x
s
Wit hout Bandwidth-Constrained Fusion E s timation
Bandwidth-Cons trained Fus ion Es t imat ion
Figure 2 ：The first component
0 5 10 15 20 25 30 35 40 45 50
-250
-200
-150
-100
-50
0
50
Ti m es /s
x
v
Without Bandwidth-Constrained Fusion Estimation
Bandwidth-Const rained Fusion Es t imation
Figure 3：The second component
Figure 2、Figure 3、Figure 4 respectively show
the estimation of the status component with
bandwidth limitation and no bandwidth limitation. It
can be seen that the fusion estimation algorithm
based on scheduling transmission strategy described
in this paper can achieve similar effect under the
condition of limited bandwidth as the estimate
without bandwidth limitation.The validity of
scheduling strategy and estimation algorithm is
verified.
0 5 10 15 20 25 30 35 40 45 50
-25
-20
-15
-10
-5
0
5
Times / s
x
a
Without B andwidth-Const rained Fusion Es t imation
Bandwidt h-Const rained Fusion Est imation
Figure 4: The third component
0 5 10 15 20 25 30 35 40 45 50
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
Tim es /s
Es timation Error Without Bandwidt h-Cons trained
Es timation Error With B andwidt h-Cons trained
Figure 5: Comparison of estimation errors
Figure 5 is the estimation error of the fusion
estimation and the true value without bandwidth
limitation and the estimation error of the fusion
estimation and the true value with bandwidth
limitation. It also shows the effectiveness of the
estimation algorithm under the scheduling strategy
proposed in this paper.
5 CONCLUSION
In this paper, a scheduling strategy of packet
transmission for multi-sensor fusion system is
proposed to solve the problem of limited bandwidth.
Firstly, the sensors in the system are divided to
multiple subsystems. Only one local optimal
estimation of subsystem can sent its measurement
information. And the other subsystems are sent
measurement periodically. The Distributed Kalman
Fusion Estimator for the system and the optimal
estimation is obtained by the way of matrix
weighting.The simulation show that the scheduling
strategy of periodic transmission of sensor
information for each group can effectively obtain the
fusion estimation value, and verify the applicability
and effectiveness of this scheduling method for
large-scale multi-sensor systems.
REFERENCES
You K, Xie L, Sun S, et al. 2011. Quantized filtering of
linear stochastic systems[J]. Transactions of the
Institute of Measurement & Control,
32(3):683-698.
Sani A,Vosoughi A.2016. Distributed Vector Estimation
for Power-and Bandwidth- Constrained Wireless
Sensor Networks[J]. IEEE Transactions on Signal
Processing, 64(15):3879-3894.
Liu G, Xu B, Chen H, et al, 2014. Adaptive quantization
for distributed estimation in cluster-based wireless
A Scheduling Strategy in Fusion Estimation with Bandwidth Constrained
239

sensor networks[J]. AEUE-International Journal of
Electronics and Communications,68(6):484-488.
Li J, Alregib G. 2009. Distributed Estimation in
Energy-Constrained Wireless Sensor Networks[J].
IEEE Transactions on Signal Processing,
57(10):3746-3758.
Schizas I D, Giannakis G B, Luo Z Q,2007. Distributed
Estimation Using Reduced Dimensionality Sensor
Observations[M]. IEEE .
Zhu H, Schizas I D, Giannakis G B. 2009. Power-Efficient
Dimensionality Reduction for Distributed
Channel-Aware Kalman Tracking Using WSNs[J].
IEEE Transactions on Signal Processing,
57(8):3193-3207.
Han D, Mo Y, Wu J, et al.2014. Stochastic
Event-Triggered Sensor Schedule for Remote State
Estimation[J]. Automatic Control IEEE
Transactions on, 60(10):2661-2675.
Han D, Mo Y, Wu J, et al. 2016. An Opportunistic Sensor
Scheduling Solution to Remote State Estimation
Over Multiple Channels[J].IEEE Transactions on
Signal Processing, 64(18):4905-4917.
Sun S L, Deng Z L. 2004,Muti-sensor optimal information
fusion Kalman fllter. Automatica, 40(6):
1017-1023.
Deng Z L, Gao Y, Mao L, Li Y, Hao G,2005. New
approach to information fusion steady-state
Kalman flltering. Automatica,2005,41(10):
1695-1707.
ICECTT 2018 - 3rd International Conference on Electromechanical Control Technology and Transportation
240