
Dynamic Reliability Analysis of Gear Vibration
R
esponse with
R
andom Parameters
Cao Tong
1
, Yuning Wang
2
, Yuanzheng Tian
1
and Changshuai Yu
1
1
State Key Laboratory of Robotics, Shenyang Institute of Automation, Chinese Academy of Sciences, Shenyang, China
2
Shenyang Aircraft Corporation, Aviation Industry Corporation of China, Shenyang, China
{Cao Tong, Yuning Wang}tongcao@sia.cn, 297410219@qq.com
Keywords: Random vibration, Gear nonlinear, Dynamic reliability, Poisson process.
Abstract: In order to study the influence of random parameters on the reliability of gear vibration, firstly, a nonlinear
stochastic vibration analysis model of gear 3-DOF gap is established based on Newton's Law. And the
random response of gear vibration is simulated by stepwise integration method. Secondly, based on the
process transcendental theory, a reliability model for the gear nonlinear vibration system with random
parametric is established. The calculation formula of the vibration reliability of gear vibration system with
random parameters is deduced and its application range is extended. The comparison of examples shows
that the parameter stochastic process has little effect on the vibration reliability of the system when the gear
system's response is periodic motion, while the vibration reliability of the system will decrease sharply
when the gear system's response is chaotic motion. This study provides a reference and theoretical basis for
the control and judgment of the nonlinear vibration of gears with random parameters.
1 INTRODUCTION
There are many nonlinear factors in the gear
transmission system, such as the gear meshing
stiffness, transmission error, bearing clearance, tooth
side gap and so on. These coupling factors will
cause the strong nonlinear vibration of the gear
system and affect the vibration reliability of the gear
system. Studies show (So, P., Ott, E., 1995; Shinbrot
T., 1993; Li W.,2012; Zhao W, 2012; Li T., 2011)
that the system will change from the periodical
response to a chaotic vibration state with chaotic,
disorder and aperiodic when the parameters of the
gear system changed a little. Generally, the gear
system response is not sensitive to the small changes
of the initial conditions in the periodic response
state, however, slight changes will make the system
vibration response produce unpredictable results
when the gear’s system enters the chaotic state.
As we all known, for the gear system with
nonlinear vibration, the change of gear’s parameters
will cause the system into a chaotic vibration state.
Traditionally, chaotic vibration state is avoided by
the conventional method (such as Lyapunov and
bifurcation method), but its dynamic state still
changes due to the randomness of gear’s parameters.
When the system is in chaotic or near-chaotic state,
random bifurcation and random chaos (Zhao W.,
2012) of the gear’s system response, which affects
the vibration and noise of the gear system and
determines the vibration reliability of the gear
system (Sun Z., 2011).
In order to avoid the chaotic vibration of the gear
system and predict the vibration reliability of the
system more accurately, the random process
characteristics of various parameters is considered
into vibration model, so as to better control or avoid
this irregular chaotic vibration characteristics. Based
on this issue of gear nonlinear vibiration, the method
of calculating the vibrational reliability of gears with
random parameters is studied in this paper. And it
provides a reference and theoretical basis for the
control and judgment of the nonlinear vibration of
gears with random parameters.
Tong, C., Wang, Y., Tian, Y. and Yu, C.
Dynamic Reliability Analysis of Gear Vibration Response with Random Parameters.
In 3rd International Conference on Electromechanical Control Technology and Transportation (ICECTT 2018), pages 241-245
ISBN: 978-989-758-312-4
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
241

2 NUMERICAL SIMULATION OF
GEAR NONLINEAR
VIBRATION SYSTEM
2.1 Model of gear nonlinear vibration
model with random parameters
To simulate the gear’s nonlinear vibration with
random parameters, the random parameter is
expressed as the combination of the determined
value and the disturbed value. For example, the
excitation frequency is equivalent to
m
+
m
,
where
m
is the determined value of the excitation
frequency,
m
, is the disturbed value of the
excitation frequency. And all parameters are
assumed as independent random variable in each
time period, namely, the dynamic response of gear
vibration is regarded as a Gaussian random process.
The three-degree-of-freedom nonlinear coupled
dynamic model (as shown in Fig. 1, the specific
derivation is shown in Ref. (Li R., 1997)) is taken as
the study object. The static transmission error is
obtained the first-order components, and the gear
nonlinear vibration model with random parameters
can be expressed as
12
p
2 p mp 11 p p 13 m
34
g
4g mg 22gg23m
56
2
1
6mm mm
24 mm 33m
d
d
22 ()()
dd
d
d
22 ()()
dd
()sin()
d
2()
d
yy
y
y
ykfykfy
tt
yy
y
y
ykfykfy
tt
yy
e
yF t
b
y
yy kfy
t
(
)
(1)
R
p
R
g
Figure 1: Dynamic model of a spur gear pair.
in which the dimensionless nonlinear function of gap
is expressed as
mm mm
mmmmm
mm mm
(),()
0,() ()
(),()
yb b b y b b b
f
y bbbybbb
yb b b y b b b
(2)
where
m
and
m
are the determined value and the
disturbed value of meshing damping ratio,
respectively
;ω
m
and ω
m
are the determined value
and the disturbed value of excitation frequency,
respectively
;b
m
and b
m
are the determined value
and the disturbed value of the tooth backlash,
respectively
;
m
、ω
m
、b
m
are similar to Gauss
white noise with zero mean.
2.2 Nonlinear vibration numerical
solution
For nonlinear random vibration analysis, the most
effective method is numerical integration method
(Zhao W., 2012; Sun Z., 2011). The numerical
simulation of nonlinear random vibration is based on
numerical integration. The step-by-step integration
method is always used to solve the system dynamics
equation, so that the solution of the system in the
time domain is obtained. There are many kinds of
step-by-step integration methods. At present, linear
acceleration method, Runge-Kutta method,
Newmark-β method and Wilson-θ method are
widely used. In this paper, the Runge-Kutta method
is used to solve the dynamic differential equations of
the system. The basic steps are:
ICECTT 2018 - 3rd International Conference on Electromechanical Control Technology and Transportation
242

(1)Determination of the basic random variables
and the distribution functions
;
(2)Let t=0, and give the initial value
(0), (0)
x
x
;
(3)Sampling the basic parameters
(4)Establishing dynamic equations of
deterministic gear system from sampling results;
(5)Solving the deterministic dynamics equation
(4) in the [t,
t+t] moment vibration displacement
and velocity by Runge-Kutta method.
3 RELIABILITY ANALYSIS OF
NONLINEAR VIBRATION OF
GEAR WITH RANDOM
PARAMETERS
3.1 Poisson Process Reliability Method
Based on Process Leaping
For the random response process, the probability of
exceeding the failed span can be respectively
expressed as follows (see (Haym B., 2005)).
2
2
()
exp
22
x
Z
xx
Zx
(3)
2
2
()
exp
2
2
x
Z
xx
Zx
(4)
22
22
() ()
exp exp
22 2
x
Z
xx x
Zx Zx
(5)
Gear vibration reliability and structural dynamic
reliability of the first failure beyond the different
amplitude of the first time beyond does not mean
that the gear structure must gear produce failure.
However, due to the periodic meshing of gears,
during the meshing cycle of gears, if the amplitude
of vibration response of gears exceeds the safety
margin for the first time, it will appear in each cycle.
If the gear system produces an excessive failure
amplitude during one meshing cycle, this amplitude
will occur during each meshing cycle, resulting in
fatigue failure of the gear.
Therefore, the vibration reliability of gear system
can be defined as: the random vibration response x(t)
within the gear meshing period (0, T
D
) under the
random factors does not exceed the maximum safety
limit Z
max
and not less than the minimum safety limit
Z
min
. It can be defined as
min max
max min
(())
(() ) (() )
RPZ xt Z
Pxt Z Pxt Z
(6)
Where
max thresholdx
ZZ
,
max thresholdx
ZZ
;
x
is the average value of random response in
steady response;
threshold
Z
is the safety margin, which
is similar to the maximum critical value in the
dynamic reliability analysis; and
max
(() )Pxt Z
and
min
(() )Pxt Z
are respectively the probability that
the number of times that the positive slope crosses
zero during the (0,t) time and the probability that the
number of times that the negative slope crosses zero.
Assuming that each transcendence is independent
and the number of transgressions N obeys Poisson
distribution, then the probability of exceeding the
number of times n in (0, t) time is
()
(,) , 0, 0
!
nt
N
te
pnt n t
n
(7)
Where, v represents the number of transcendence
occurred within a unit of time.
(1) The probability of crossing the number of
times is zero with positive slope within
D
tT
(
max
(() )Pxt Z
)
Considering the characteristics of the Poisson
process, if the stochastic process x(t) crosses the
positive slope at each pass through
max
Z
, the upper
pass rate
Z
is equal to the parameter v. The
probability density function of the number of times
over the number of
Z
N
is expressed as
()
(,) , 0, 0
!
Z
Z
t
n
Z
N
te
pnt n t
n
(8)
Then the probability of crossing the number of
times is zero with positive slope within
D
tT
max
(() ) (0, )
Z
D
Z
T
D
N
Pxt Z p T e
(9)
Substituting Eq.(3) into Eq. (9), then
2
max
max
2
()
(() ) exp exp
22
xD
xx
TZx
Pxt Z
(10)
(2) the probability of crossing the number of
times is zero with positive slope within
D
tT
(
min
(() )Pxt Z
)
If the stochastic process x(t) crosses the negative
slope at each pass through
max
Z
, the upper pass rate
Z
is equal to the parameter v. The probability
density function of the number of times over the
number of
Z
N
is expressed as
Dynamic Reliability Analysis of Gear Vibration Response with Random Parameters
243
()
(,) , 0, 0
!
Z
Z
t
n
Z
N
te
pnt n t
n
(11)
Then the probability of crossing the number of
times is zero with positive slope within
D
tT
min
(() ) (0, )
Z
D
Z
T
D
N
Pxt Z p T e
(12)
Substituting Eq.(4) into Eq. (12), then
2
min
min
2
()
(() ) exp exp
22
xD
xx
TZx
Pxt Z
(13)
3.2 Calculation and Analysis of Gear
Dynamic
Take a typical gear example as the object of this
study, the values of the parameters in the differential
equation of gear vibration are taken as follows:
m
=0.05, b
m
=0.07, ω
m
=0.75,
p
=0.01,
g
=0.01, b
p
=0,
b
g
=0, e
1
=0.01. The gear system under the above
parameters of the random vibration system is called
'case one'. The dynamic response of the nonlinear
vibration system with random parameters is
calculated by the numerical simulation method in
Section 2.2, and the dynamical response is shown in
Figure 2.
The reliability method which is described in
Section 3.1 is used to calculate the reliability of gear
vibration response with random parameters:
x
x
=0.15745,
threshold
Z
=0.05,
max
x
Z
threshold
Z =0.20745,
min x
Z
threshold
Z
=0.10745.
Other calculated parameters are T
D
= 8.3775,
x
=
0.014922,
x
=0.01291. According to Eq. (6), the
reliability of gear dynamic vibration is R=0.9916171.
Figure 2: Time history of periodic vibration response for
gear system with random parameters (Case one).
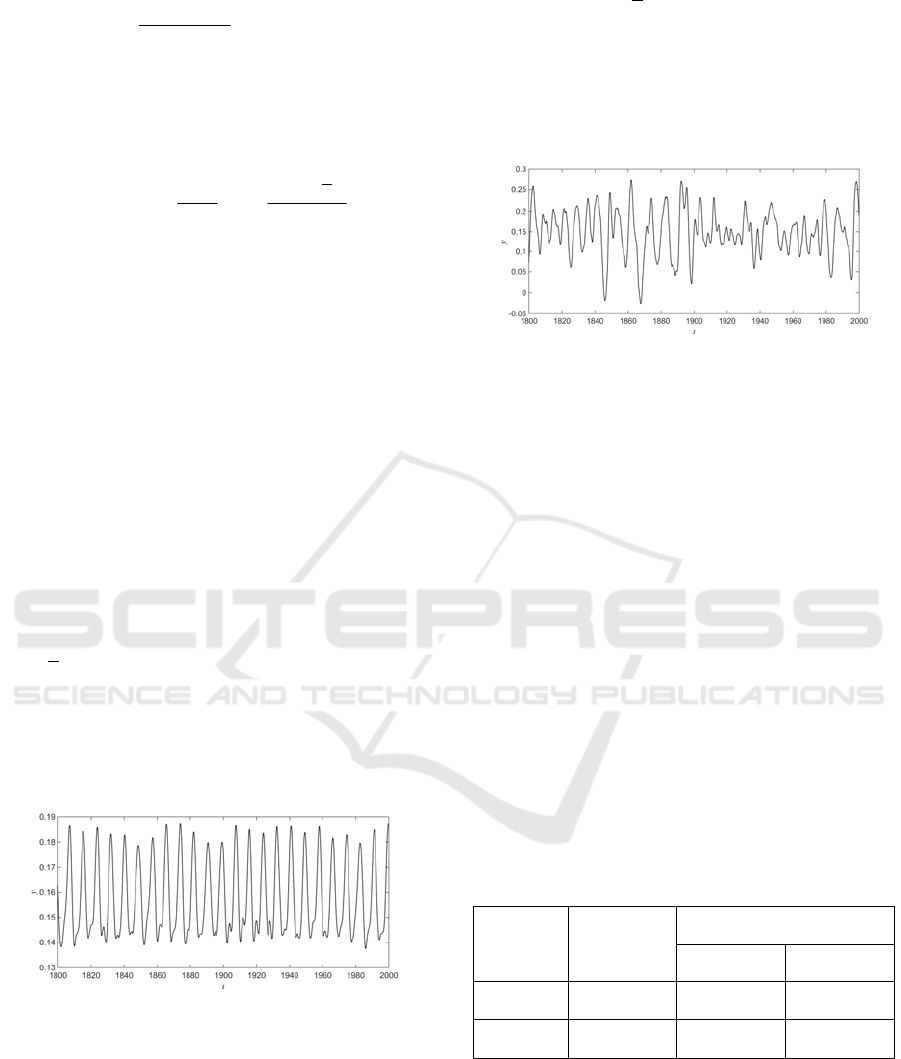
When
m
=1.55, other parameters of the current
nonlinear gear system remain unchanged, the gear
system is in a chaotic vibration state. Figure 3
corresponds to the gear system dynamic response
time history curve. The reliability method which is
described in Section 3.1 is used to calculate the
reliability of gear vibration response with random
parameters:
x
x
0.14856,
threshold
Z
=0.05,
max
x
Z
threshold
Z
=0.19856,
min x
Z
threshold
Z
=0.04977. Other calculated parameters are T
D
=
4.0537,
x
= 0.05651,
x
= 0.01291. And according
to Eq. (6), the reliability of gear dynamic vibration is
R=0.4638098.
Figure 3: Time history of periodic vibration response for
gear system with random parameters (Case two).
Table 1 shows the reliability of different random
vibration system response results. By comparison, it
is found that the parameter stochastic process has
little changes on the vibration reliability of the
system for the case one (gear vibration response in a
periodic motion). However, for the second case (the
vibration response of the gear is chaotic), the
vibration reliability rapidly decreases from
0.9417517 to 0.4638098 due to the random process
characteristics of the parameters. Results show that
chaotic motion system itself is very sensitive to
small changes of obove parameters, and the
randomness of parameters will lead to the changes
of gear dynamic response, so as to cause the
individual amplitude of vibration response to be too
large. This unpredictable result, which is sensitive to
the initial parameters, is in good agreement with
chaos theory.
Table 1: Calculation results of each random vibration
system
System
type
Response
type
Reliability calculation
results
Determined
parameters
Random
parameters
Case one Periodic
motion
0.9911982 0.9916171
Case two Chaotic
movement
0.9417517 0.4638098
4 CONCLUSIONS
In this paper, the numerical simulation of gear
nonlinear vibration system with random parameters
are carried out. The calculation formula of the
ICECTT 2018 - 3rd International Conference on Electromechanical Control Technology and Transportation
244

vibration reliability of gear vibration system with
random parameters is deduced and its application
range is extended. The comparison of examples
shows that the parameter stochastic process has little
effect on the vibration reliability of the system when
the gear system's response is periodic motion, while
the vibration reliability of the system will decrease
sharply when the gear system's response is chaotic
motion.
This study will provide a reference and
theoretical basis for the control and judgment of the
nonlinear vibration of gears with random parameters.
ACKNOWLEDGEMENTS
The study was supported by the State Key
Laboratory of Robotics (No. Y7C1207301), and its
financial support is gratefully acknowledged.
REFERENCES
So, P., Ott, E., 1995. Controlling chaos using time delay
coordinates via stabilization of periodic orbits.
Physical Review E, 51(4): 2955.
Shinbrot T., Grebogi C., Ott E., 1993. Using small
perturbations to control chaos. Nature, 363(6428):
411-417.
Li W., Ma J., Di C., 2012. Simulatron research on
dynamics of ranmmng system and action reliability
considering the randomness of the parameters. Acta
Armamentarii, 33(6): 747-752.
Zhao W., Zhang Y. M., 2012. Reliability sensitivity of
vibration transfer path systems. Journal of Aerospace
Power, 27(5): 1080-1086.
Li T., Zhu R., Bao H., 2011. Nonlinear torsional vibration
modeling and bifurcation characteristic study of a
planetary gear train. Chinese Journal of Mechanical
Engineering, 47(21): 76-83.
Zhao W., Zhang Y. M., 2012. Reliability sensitivity of
vibration transfer path systems. Journal of Aerospace
Power, 27(5): 1080-1086.
Sun Z., Yuan Z., 2011. Reliability Analysis of Nonlinear
Vibration Response for Gear System with Stochastic
Parameters[J]. Journal of Northeastern University
(Natural Science), 6: 021.
Li R., Wang J., 1997. The book, Gear system dynamics.
Haym B., Seon M. H., 2005. The book, Probability models
in engineering and science.
Dynamic Reliability Analysis of Gear Vibration Response with Random Parameters
245
