
Research on the Controllabilit
y
of Urban Road Networ
k
Chuanci Cai and Xuan Zhang
School of Traffic and Transportation, Beijing Jiaotong University, Beijing100044, China
{16120778, 15120925}@bjtu.edu.cn
Keywords: Urban road network, controllability, network topology, PBH theorem.
Abstract: In order to study the factors influencing the controllability of urban road network, the paper calculates the
network topology features of the real urban road networks and the simulated urban road networks, such as
average degree, 2-core, clustering coefficient, heterogeneity, organic ratio and meshedness coefficient.
According to the PBH judgment theorem and the minimal control input theorem, the minimal number of
control inputs and the network controllability are obtained. Then the correlation between network
controllability and topological characteristics is analyzed. It is found that heterogeneity, 2-core and average
degree have a great influence on controlling the urban road network. The results show that it is of great
significance to balance the function, strengthen the connectivity and regularity of network to ensure the
orderly operation of urban road network.
1 INTRODUCTION
Urban traffic system is a typical open complex giant
system. It is composed of road network, traffic flow
and management control system. The topological
structure of road network directly affects the
characteristics of traffic flow dynamics. Numerous
studies show that most urban road networks are
scale-free networks and exhibit small-world
characteristics (Lämmer et al., 2006; Porta et al.,
2006; Jiang, 2007). Changes in the network structure
will affect the operation of the network (Arrowsmith
et al., 2005; Kwangho et al., 2005).
Motter et al. (2008) study the metabolic networks
of single-celled organisms, where disturbances
caused by genetic or epigenetic defects can lead to
unfeasible strains. By knocking out specific genes,
the consequences of these defects can be alleviated
and the ability of the strain to grow can be restored;
Sahasrabudhe and Motter (2011) study food
networks. As we know, human or natural forces may
lead to the subsequent extinction of many species.
The study shows that a significant proportion of
these extinctions can be prevented by targeted
inhibition of specific species in the system; These
findings have similarities in the power grid.
Equipment failure, damage or operational errors can
lead to widespread blackouts, but proper power
release can greatly reduce subsequent failures
(Anghel et al. 2006).
Therefore, to alleviate traffic congestion and
ensure the orderly operation of urban road network,
it is necessary to study the relationship between the
controllability of urban road network and the
network topology features.
2 THEOREM
2.1 PBH judgment theorem
The necessary and sufficient condition for a
continuous linear time invariant system to be strictly
controlled is that the system matrix satisfies the
following rank condition:
rank
λ
A,B
N
(1)
λ is the eigenvalue of the coupling matrix A.
2.2 Theorem of minimal control input
According to the PBH judgment theorem, B is the
input matrix, so we can get the minimum number of
inputs: N
min
rank
B
. Using the inequality
relation of the matrix rank, the algebraic multiplicity
δ
λ
of the eigenvalue λ
is the occurrence times of
λλ
in the factorization of P
λ
det
λI
A
. The geometric multiplicity μ
λ
is
the dimension of the corresponding Characteristic
334
Cai, C. and Zhang, X.
Research on the Controllability of Urban Road Network.
In 3rd International Conference on Electromechanical Control Technology and Transportation (ICECTT 2018), pages 334-338
ISBN: 978-989-758-312-4
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

subspace V
α|Aα λ
α
. Therefore, we obtain
the geometric multiplicity μ
λ
N
rank
λ
I
A
and the minimal number of control
inputs is calculated as follows:
N
μ
λ
(2)
Through this theorem, we can use the
eigenvalues of the system coupling matrix A to
determine the controllability of the original system.
Moreover, by using the PBH theorem, the minimal
number of control inputs and the corresponding
driving nodes for the system to be strictly controlled
is theoretically obtained (Yuan, 2014).
2.3 Minimal control inputs of sparse
network
The geometric multiplicity of zero eigenvalue is
μ
0
NrankA, and we can get the minimal
number of inputs in sparse networks:
N
max
1,Nran
k
A
(3)
The real road network and simulated road
network in this paper are regarded as sparse
networks. The calculation method of minimal
control input number adopts the formula (3).
2.4 Controllability
The controllability of the network refers to the
proportion of the drive nodes in the network:
n
N
/N
(4)
The controllability of the network reflects
controllable difficulty of the network from the
demand of the control inputs. The smaller the n
is,
the easier it is to control the network. Otherwise, the
larger the n
is, the harder it is to control the
network.
3 TOPOLOGY FEATURES
Average degree
k
is the average of the degree k
of all nodes i in the network. The calculation method
is shown in equation (5), where a
denotes the exit
of node i.
k
1
N
k
1
N
a
,
(5)
Clustering coefficient C
refers to the ratio of the
actual number of edges and the total possible
number of edges between k nodes.
1/2
2
1
(6)
Heterogeneity can characterize the uniformity
of node distribution. When H = 1, the distribution of
network degree is the most uniform. When H = 0.5,
the distribution of network degree is the most
disorder (Wu et al., 2007). The calculation method is
as shown in formula (7) .
H
∑
q
k
lnq
k
lnN
(7)
Meshedness coefficient M
is used to measure
the network topology (Courtat et al., 2010). e is the
number of edges in the network, v is the number of
nodes in the network, N
2
is the number of nodes
with a degree of 2 in the network.
M
e
v
1
2∗
v
∗1N
2
5
(8)
Organic ratio
is used to determine whether a
city has been planned, as shown in formula (9).
Where N (j) denotes the number of nodes with
degree j in the network.
γ
N
1
N3
∑
Nj
(9)
k-core refers to the union of k-shells whose k
k (Wang et al., 2012).
4 CORRELATION ANALYSIS
4.1 Real urban road network
The road network coordinates of Beijing, Berlin,
Manchester, London, Chicago and Singapore are
extracted from the Open Street Map. Use Python
programming to generate each city's road network.
The roads in the network are regarded as edges and
intersections as nodes. The road networks generation
map for the six cities are shown in Figure 1.
Research on the Controllability of Urban Road Network
335

(a) Beijing (b) Berilin
(c) Manchester (d) London
(e) Chicago (f) Singapore
Figure 1: Urban road network.
The controllability and the network topology
features such as average degree, 2-core, clustering
coefficient, heterogeneity, meshedness coefficient
and organic ratio of the above six cities are
calculated, the results are shown in Table 1. Analyze
the correlation between controllability and network
topology features, the Pearson correlation
coefficients between controllability and the above
topological features are -0.574821, -0.702653
0.262591, -0.202581, -0.102783, -0.802577
respectively. It can be found that the controllability
of the network has a great negative correlation with
the average degree, 2-core and heterogeneity.
4.2 Simulated urban road network
Through the analysis of the real road network, it can
be found that the controllability has a great
correlation with some network topological features.
In the following, we will use simulated urban road
network to verify the above results.
The research on network evolution mechanism is
an important means to explore the network
formation mechanism. It mainly involves five kinds
of events in the evolution of networks: adding nodes,
adding edges, reconnecting, removing edges, and
removing nodes. Researches on small-world
network model and scale-free network model in this
respect are of groundbreaking significance. Studies
have shown that as the network size increases, the
controllability of the network becomes smaller.
Therefore, this paper starts with the evolution of
road network and studies the influence of topology
characteristics on the network controllability as the
network size changes. Mainly include the urban road
network evolution model (Barthelemy and
Flammini, 2007) and the urban road network model
based on β-Skeleton structure (Osaragi and Hiraga,
2011).
4.2.1 Road network based on the evolution
model
Figure 2: The optimal principle of urban road network
evolution model.
At a given stage of the road network evolution,
two nodes A and B still need to be connected to the
network. At any time step, each new node can
trigger the construction of a single new portion of
road of fixed length. In order to maximally reduce
their distance to the network, both A and B would
select the closest points M
and M
in the network as
initial points of the new portions of roads to be built.
If M
and M
are distinct, segments of roads are
added along the straight lines M
A and M
B. If M
= M
= M, it is not economically reasonable to build
two different segments of roads and in this case only
one single portion MM′ of road is allowed. The
main assumption here is that the best choice is to
build it and maximize the reduction of the
cumulative distance ∆ from M to A and B, as shown
in Figure 2.
∆
d
M,A
d
M,B
d
M
,A
dM
,B
(10)
The maximization of ∆ is done under the
constraint |MM′| = const. << 1.
ICECTT 2018 - 3rd International Conference on Electromechanical Control Technology and Transportation
336
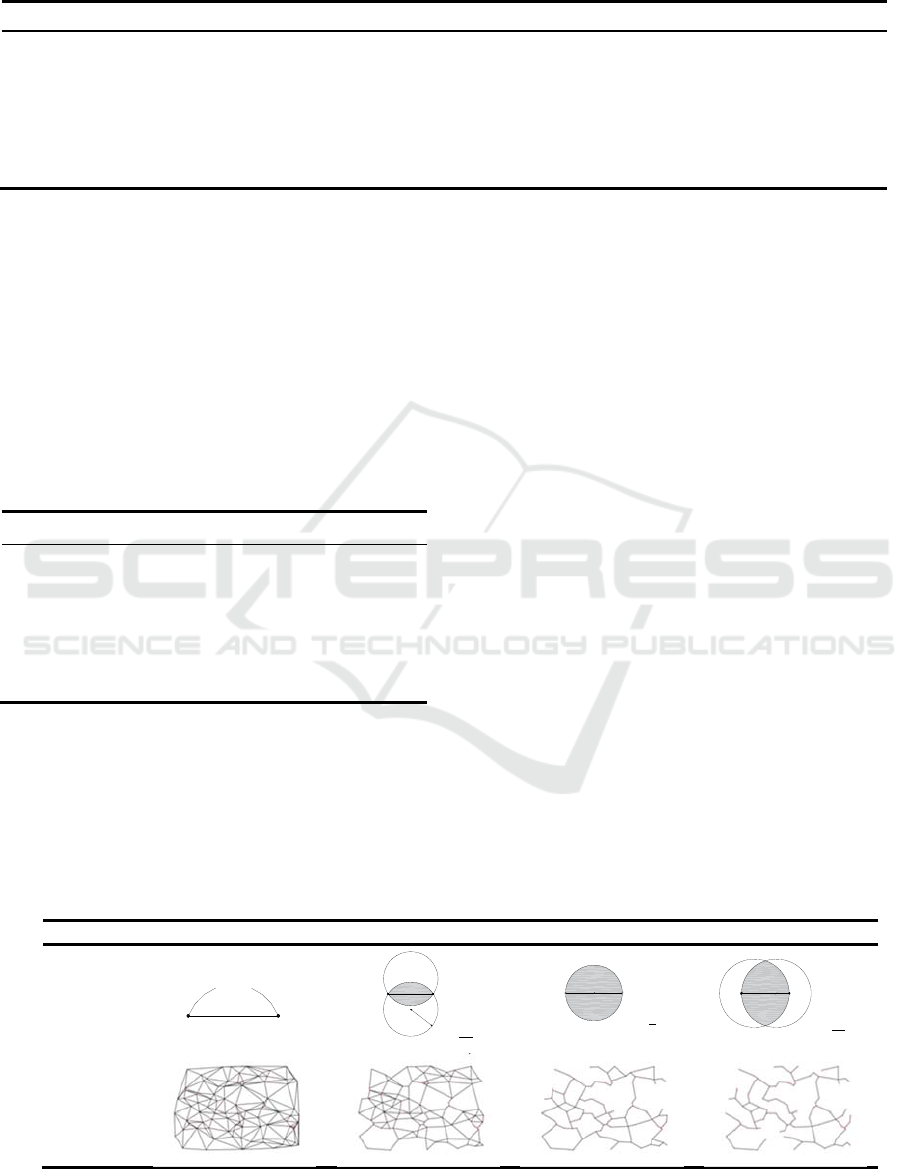
Table 1: The topology features of urban road network.
city\parameter
k
2-core
C
γ
M
H n
Manchester 3.2538 0.8914 0.1080 0.5138 0.2884 0.9922 0.0245
Berlin 3.1689 0.8733 0.0773 0.4955 0.3017 0.9914 0.0178
Singapore 3.2148 0.9065 0.0603 0.5359 0.3082 0.994 0.0105
Beijing 3.1069 0.8265 0.0528 0.3781 0.2798 0.9893 0.0222
London 3.2456 0.9287 0.0902 0.5837 0.3147 0.9948 0.0132
Chicago 3.3705 0.9223 0.0770 0.4186 0.3477 0.9950 0.0089
When the growth rate is taken as 0.2 and the
distribution of nodes is uniform, the network
controllability analysis under different network size
is carried out. Through correlation analysis, it can be
found that the controllability of the road network
generated by the evolution model shows a large
negative correlation with the average degree, 2-core
and the heterogeneity. The Pearson correlation
coefficients were -0.758669, -0.941210, -0.904039,
respectively.
Table 2: Network topology features of evolutionary
network.
Size
2-core
50 1.9758 0.400 0.96888 0.1400
80 1.9958 0.625 0.96842 0.1375
100 1.9983 0.700 0.96618 0.1300
150 2.0002 0.800 0.96577 0.1267
180 2.0390 0.833 0.96530 0.1222
200 2.1602 0.875 0.96529 0.1200
4.2.2 Road network based on the β-skeleton
βskeleton structure: given a point distribution
p
i 1,2,…,n in a two-dimensional plane, and
randomly connect these points to form a side to
create a geometric map. Assuming that there are two
arcs passing through any point p
and p
, the size of
the intersecting region E of the two arcs increases as
the parameter β increases. It is determined whether
or not a third point is included in the area. If there is
a third point, the line segment between the points p
and p
is not the edge of the network and needs to
be deleted. If there is no third point, Then the line
segment between points p
and p
exists as a side of
the network.
The form of the network with different
parameters β is shown in Table 3. Whenβ 0, the
shape of the network is Delaunay triangulation
graph; when β∈0,1, the shape of the network is
Gabriel graph; when β∈1,2, the shape of the
network is the Relative neighborhood graph; when
β2, the shape of the network is the spanning tree
graph .
Because when β∈1,1.5, the simulated urban
road network model based on β-Skeleton structure
has the maximum similarity with the real urban road
network. So this paper carries out the network
controllability analysis under β1.5. Through
correlation analysis, it can be found that the
controllability of the road network generated by the
β-Skeleton structure also shows a large negative
correlation with the average degree 、 2-core and
heterogeneity. The Pearson correlation coefficients
were -0.990535, -0.945245, -0.966129 respectively.
Table 3: The definition of β-skeleton.
β β0 0β1 β1 β1
Definition
L
p
1
p
2
p
1
p
2
r
r =
L
2
β
p
1
p
2
r
r =
L
2
p
1
p
2
r =
Lβ
2
r
r
Network
Research on the Controllability of Urban Road Network
337

Table 4: Network topology features of β Skeleton
network.
Size
k
2-core
H n
50 2.6000 0.9400 0.9849 0.0400
80 2.7250 0.9500 0.9898 0.0250
100 2.7400 0.9500 0.9895 0.0200
150 2.8267 0.9667 0.9923 0.0133
180 2.8556 0.9722 0.9927 0.0111
200 2.8800 0.9750 0.9926 0.0050
5 CONCLUSION
Based on the theory of complex network, this paper
uses the PBH judgment theorem and the minimal
control input theorem to analyze the network
topology features of real and simulated road
network. It is found that network average degree, 2-
core and heterogeneity are strongly related to the
controllability of the network. Increasing the average
degree will improve the synchronization ability of
the network as well as the range of propagation. 2-
core can help to distinguish the truly important core
nodes in the actual network. Reasonable control of
network heterogeneity can improve the network
anti-congestion ability. Therefore, it is of great
significance to control the orderly operation of urban
road network by rationally configuring the number
of intersections and the number of road intersections.
It is also of great importance to control the size of
the network and the capacity of the road and
strengthen the connectivity of the network.
REFERENCE
Lämmer, S., Gehlsen, B., and Helbing, D., 2006. Scaling
laws in the spatial structure of urban road networks.
Physica A Statistical Mechanics & Its Applications,
363(1):89-95.
Porta, S., Crucitti, P., and Latora, V., 2006. The network
analysis of urban streets: A dual approach.
Environment & Planning B Planning & Design,
33(2):853-866.
Jiang, B., 2007. A topological pattern of urban street
networks: Universality and peculiarity. Physica A:
Statistical Mechanics and its Applications,
384(2):647-655.
Arrowsmith, D.K., Bernardo, M. D., and Sorrentino, F.,
2005. Effects of variations of load distribution on
network performance. Eprint Arxiv Cs, Vol. 4:3773 -
3776.
Park, K., Lai, Y., and Zhao, L., 2005. Jamming in complex
gradient networks. Physical review E, Statistical,
nonlinear and soft matter physics, 71(6 Pt 2):065105.
Motter, A. E., Gulbahce, N., and Almaas, E., 2008.
Predicting synthetic rescues in metabolic networks.
Molecular Systems Biology, 4(1):168-168.
Sahasrabudhe, S., & Motter, A. E., 2011. Rescuing
ecosystems from extinction cascades through
compensatory perturbations. Nature Communications,
2(11), 170.
Anghel, M., Werley, K. A., and Motter, A. E., 2007.
Stochastic Model for Power Grid Dynamics. 40th
Hawaii International Conference on System Sciences.
IEEE.
Yuan, Z.Z., 2014. Research on the control of complex
networked system. Beijing: Beijing Normal University.
Wu, J., Tan, Y.J., Deng, H.Z., 2007. Normalized entropy
of rank distribution: a novel measure of heterogeneity
of complex networks. Chinese Physics B: English,
16(6):156-1580.
Courtat, T., Gloaguen, C., Douady, S., 2010. Mathematics
and Morphogenesis of the City: A Geometrical
Approach. Phys. Rev. E, 83, 036106.
Wang, X.F., Li, X., Chen, G.R., 2012. Network Science:
An Introduction. Higher Education Press. Beijing, 1st
edition.
Wang, X.F., 2006. Complex Network Theory and Its
Applications.Tsinghua University Press. Beijing, 1st
edition.
Barthelemy, M., & Flammini, A., 2008. Modeling urban
streets patterns. Phys. Rev. Lett., 100, 138702.
Osaragi, T., Hiraga, Y., 2011. Road Network Analysis
using Geometric Graphs of β-skeleton. 11th
international conference on GeoComputation.
ICECTT 2018 - 3rd International Conference on Electromechanical Control Technology and Transportation
338
