
The Application of Wavelet Analysis in Ultrasonic Nondestructive
Testing
Huanxin Cheng
1
, Junliang Liu
1
and Li Cheng
2
1
College of Automation and Electrical Engineering, Qingdao University of Science and Technology, Qing
Dao266042, China
2
Xinjiang Technical Institute of Physics and Chemistry, Chinese Academy of Sciences,
No 40-1 Bei
j
in
g
Rd, Urumqi, Xin
j
ian
g
, 830011, chen
g
li
@
ms.x
j
b.ac.cn
Keywords: Wavelet Analysis, Ultrasonic nondestructive testing, Singularity, Bridge detection, Simulation.
Abstract: Ultrasonic detection during the operation is inevitably influenced by ambient temperature and the noise,
causing the received ultrasound signal low signal-to-noise ratio, great error in actual and theoretical
waveform. For getting right ultrasonic feedback energy and the acquired signals, in this paper, the wavelet
singularity detection method is used to detect mutation signal and threshold value to noise method is used to
remove noise, meeting the nature of the time-domain and frequency-domain simultaneous analysis, and the
MATLAB simulation is used to compare the advantages of Fourier denoising method and the wavelet
denoising method, showing that the wavelet denoising method has incomparable advantages in bridge
detection to noise processing.
1 INTRODUCTION
Ultrasonic detection is ultrasonic excited by
interference source, it is changed according to the
detection principle of acoustic characteristics using
the object itself or the internal defects of the
ultrasonic propagation, in the case of damage
detection, object internal and surface defects in shape,
size, shape and distribution in determination of
material characteristics, can be positioned on the
workpiece, the surface and internal defects
assessment, detection and diagnosis. However, in
practical engineering applications, most of the
environmental incentives are non-stationary, and the
frequency part of the response signals varies
according to time. For the nonstationary signals, are
now commonly used in frequency domain and time
domain identification methods can not meet the
signal in time and frequency domain at the same time,
two partial analysis of the demand (Chen, 2010),
wavelet analysis algorithm can effectively overcome
this shortcoming, it is realized through analyzing the
time-varying characteristic of the systems according
to the wavelet analysis and denoising the image can
display the presence of damage. Introducing wavelet
analysis into the damage identification of civil
engineering structure can improve the accuracy and
accuracy of damage identification. It has become the
main means of health inspection for engineering
structures.
2 WAVELET TRANSFORM AND
THE THEORY OF SINGULARIT
2.1 Wavelet transform and the theory of
singularity
Set Ψ
∈
R
. Its Fourier transform Ψ
(ω),whenΨ
(ω)Meet the permissible conditions:
C
Ψ
Ψ
ω
ω
dω ∞
∞
(1)
We callΨ
as a basic wavelet or Mu Xiaobo.
The generating functionΨ
dilation and translation
after we get:
Ψ
,
√
Ψ
, ∈ R; 0(2)
This is a wavelet sequence, in the case of different
scales. The duration of the wavelet widened with the
increase of a. The amplitude decreases with the
increase of
√
, but the basic shape of wave (Lin,
2011) remain unchanged.
For any function
∈
, The definition of
continuous wavelet transform is:
Cheng, H., Liu, J. and Cheng, L.
The Application of Wavelet Analysis in Ultrasonic Nondestructive Testing.
In 3rd International Conference on Electromechanical Control Technology and Transportation (ICECTT 2018), pages 387-390
ISBN: 978-989-758-312-4
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
387

,
ΨΨ()(, = , )
1
Ψ3
(
axb
twab x dtx
tb
d
a
a
t
t
)
The representation of the inner product
mathematically is
and Ψ
,
of of similar
degree
When the scale a increases, expressed by stretching
Ψ
Waveform to observe of the whole
; on the
contrary, when the scale of a is reduced, indicated by
compression the only Ψ
waveform to observe
the
of the local, therefore, can be used as a
signal to the different scales of the wavelet transform
in general analysis (Zhang, 2007).
Lipschitz exponent is used to characterize the
singular properties of singularity (Ren, 2005). The
Lipschitz index is defined as: Set n as an integer, n
α n+1, The signal
is Lipschitz a at t(0). If
there are A and h0>0and N sub polynomials pn (h),
so that all h<h0, there are:
|
|
(4)
In which pn(h) is the former n term of the Taylor
series of X (T) at t0.
The greater the Lipschitz exponent α the higher the
smoothness of the function at this point; the lower the
smoothness, the greater the singularities, the greater
the . The Lipschitz index defines the accurate
information of the signal
i n t h e
point,
that is, smoothness, which effectively improves the
accuracy of identification of damage. Change
schematic diagram.
2.2 Wavelet threshold de-noising
algorithm
The wavelet threshold de-noising algorithm can get
the best estimation in Besov space which is more
accurate than other linear estimation methods.
A one - dimensional model of noise - containing
signals can be expressed as:
)()(s(i) ieif
i=0,1,...,n-1 (5)
Type,
)(if
represent useful signals,
)(ie
r ep re se nt
noise signal,
is noise level coefficient.
The wavelet threshold denoising algorithm includes
hard threshold denoising and soft threshold de-
noising, and the hard threshold is defined as:
,
|
|
0,
|
|
(6)
The soft threshold is defined as:
sgn
|
|
,
|
|
0,
|
|
(7)
Among, is threshold or threshold value.Our noise
is roughly as follows: select the appropriate wavelet
decomposition of noise signal; after wavelet
decomposition, the noise signal will be included in
the high frequency coefficients in the selection of
appropriate threshold; the decomposed high
frequency coefficients of high-frequency coefficients
of wavelet decomposition of signal reconstruction
process, finally completed the noise reduction.
3 DETECTION OF CRACKS IN
BRIDGES IN CIVIL
ENGINEERING BY USING
WAVELET TRANSFORM
3.1 The establishment of mechanical
model of simple supported beam
In order to replace a simple supported beam with a
crack with an elastic hinge, a mechanical model with
a simple supported beam with a crack, is established.
Stiffness of elastic hinge is
:
, C =
.
, δ
, among, is fracture
depth, is cross section height, E is modulus of
elasticity, is section inertia moment ,
is:
1.8624
3.95
16.37
37.226
76.81
126.9
172
143.97
66.56
(8)
The cracks in the model divide the beams into two
parts,(9),(10) formula represent respectively the two
parts of the free vibration is(To the left as the origin
of coordinates):
η
cos
sin
(9)
η
cos
sin
(10)
Among,
ω^2ρA/EI , ω is vibrational circle
frequency, ρ is material quality, A is cross section
area,
,
,
,
,
,
,
,
is coefficient, i s
calculation of the distance from the cross section to
the left support. The boundary of the simple
supported beam is in accordance with:
η
0
0,
0
0,η
0,
0.
The crack section should be satisfied:
η
η
(11)
(12)
(13)
(14)
Among, represents the total length of a beam,
represents the gap between the crack section and the
ICECTT 2018 - 3rd International Conference on Electromechanical Control Technology and Transportation
388
left bracket.
Bring the formula(9),(10) into the boundary
condition(11)~(14), you can get a set of equations on
,
,
,
,
,
,
,
, the coefficients of the
equation of vibration can be known.
3.2 Identification of simple supported
beam cracks by wavelet analysis
Span of simple supported beam is 800mm, Cross
section size is 20mm*40mm, it is known that there is
a crack at the left support 300mm, The depth of the
crack δ
respectively is 0.1、0.2、0.3、0.4、0.5、
0.6. Continuous wavelet transform from scale 1 to 25,
from this, we can get the maximum value of the
wavelet coefficients at the fracture section of each
scale, The modulus maximum of the wavelet
coefficients increases with the increase of the scale,
and is nonlinear. The Lipschitzα exponent can be
obtained by the logarithm of the modulus maximum
of the wavelet coefficients, and the Lipschitz α
exponent decreases with the increase of the depth of
the crack.(
Zhu, 2008) The crack singularities can be
obtained from the Lipschitzαexponent, the damage
degree of the crack beam can be judged.
4 SIMULATION CONTRAST OF FU
LIYE DE-NOISING AND
WAVELET DENOISING
The traditional way of Fourier denoising is to
transform the signal to Fourier transform first, then
low-pass filter, and finally reconstruct the (Shyu,
1996) of the signal after Fourier transform. This
method has very obvious shortcomings, the useful
signal is mainly concentrated in the low-frequency
part, the noise signal is mainly concentrated in the
high-frequency part, but also the useful signal is a
high frequency part, if using a simple low-pass filter,
high frequency part will be a useful signal with noise
signal to filter out, if using low pass filter in order to
save the narrow high-frequency part of the useful
signal, then the signal is filtered will still exist a lot of
noise signal, and the whole process is performed in
frequency domain, without time domain information.
Wavelet analysis can effectively combine the time
domain with the frequency domain(Zhang, 2008), In
the previous chapter, the wavelet threshold denoising
algorithm is introduced. To verify the superiority of
the wavelet denoising method, we select a segment of
Doppler signal, add white noise to it, then the Fourier
denoising and wavelet denoising are used
respectively,in this example, we use the MATLAB7.0
platform for simulation,use Sym8 wavelet
decompose three layers, wavelet coefficient threshold
quantization is quantified by heursure soft threshold.
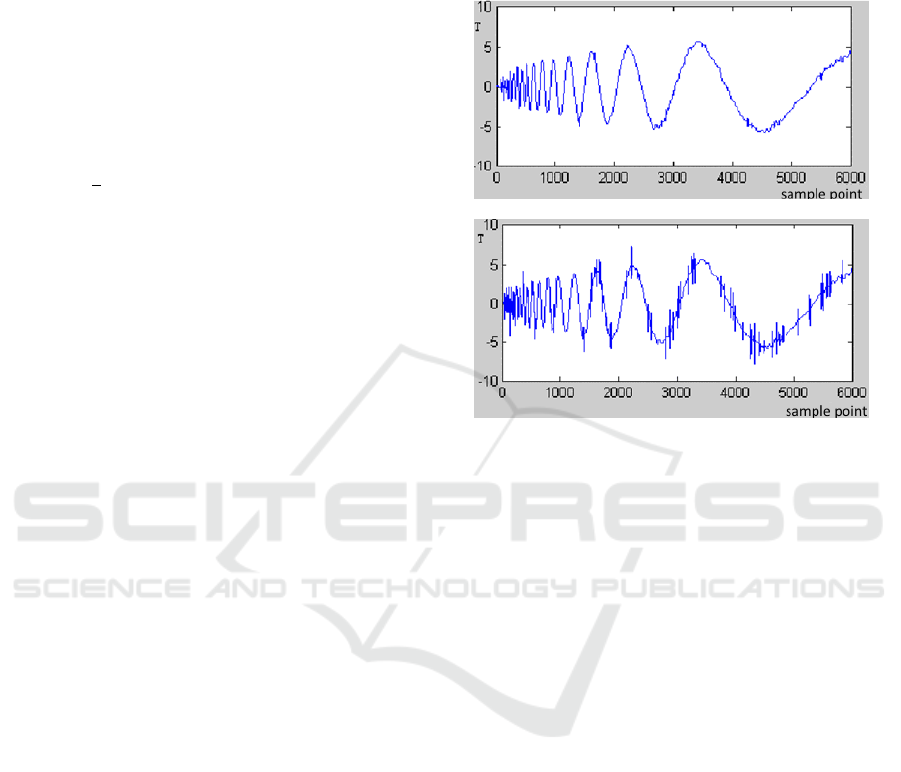
Fig.1 Effect of Wavelet Denoising
Fig.2 Effect of Fourier Denoising
It can be seen from the diagram, compared to the
Fourier denoising method, it is ideal to obtain the
overall trend of the signal by the wavelet transform
de-noising method. Its basic idea is the function of the
bandpass filter based on the wavelet transform, The
signal is decomposed into different translation and
scaling wavelet or base functions and the wavelet
analysis has the window function is not the same,
with the local analysis ability is very good, can be
found that no other signal analysis methods of the
observed discontinuity and the breakpoint, thus
removing burr noise the.
5 CONCLUSIONS
In this paper, the method of ultrasonic sampling is
studied, and the theory of wavelet transform is used
as the main research method.,the damage degree of
the cracked simple supported beam is judged, and the
wavelet threshold de-noising of the sampled signal is
carried out. Through MATLAB simulation, the Fu
Liye denoising method and wavelet analysis
denoising method are compared. It shows that the
wavelet analysis has the advantage that Fu Liye can
not get rid of noise in bridge detection and denoising.
The research method has been applied to the design
of virtual wavelet de-noising instrument and the
design of ultrasonic nondestructive flaw detector. It
The Application of Wavelet Analysis in Ultrasonic Nondestructive Testing
389

effectively improves the accuracy and accuracy of
damage identification, and effectively maintains the
ultrasonic signal.
REFERENCES
Chen Dong-di, Xiang Jia-wei, A summary of operational
modal analysis methods [J], Journal of Guilin
University of Electronic Technology, 2010,(2):163-167
Lin Ya-ting, application of new threshold function in signal
and image denoising [D], [Dissertation] Xiamen:
Xiamen University, 2011
Zhang Ping,Shan Xiu-ming, extraction of [J] based on the
wavelet multiresolution analysis of geomagnetic
pulsation signals, earthquake research, 2007,(2):179-
181
Ren Yi-chun, Yi Wei-jian, research on the identification of
beam cracks based on wavelet analysis [J], Journal of
computation44al mechanics, 2005, (4): 399-464
Zhu Yan-qin, Yang Xian-lin, several improved methods
based on wavelet threshold de-noising [J], electronic
test, 2008, (2): 18-22.
H. F.Shyu, M. W. B .Lock. Ultrasonic backscattering
system with split-spectrum processing for HAZ creep
damage evaluation. Insight,1996, 38(2):91-95
Zhang Li-zhen, application of signal fast band pass filtering
in ocean signal analysis [J], marine science progress,
2008, (1): 18-25.
ICECTT 2018 - 3rd International Conference on Electromechanical Control Technology and Transportation
390
