An Evaluation of Swarm Robotic Cooperative Target Search

Shijie Lu and Yingguang Hao

School of Information and Communication Engineering, Dalian University of Technology, Dalian, MyTown, China

lushijie@mail.dlut.edu.cn

Keywords: Swarm Robotics, Particle swarm optimization, Auxiliary orientation, Roaming algorithm.

Abstract: To search for multiple targets with swarm robots, those robots should be divided into some sub-swarm by job

allocation, so that each sub-swarm can cooperatively work focusing on its desired target. Each sub-swarm

searches for its target by evolutionary algorithm. In order to improve the cooperative search ability of sub-

swarm, a new particle swarm algorithm based on auxiliary orientation improvement is proposed to enhance

the efficiency and accuracy of the search. In the simulation, the general roaming algorithm consumes a longer

time to find the target, and reduces the overall efficiency of the system. In order to solve this problem, a spiral

roaming method based on artificial potential field is introduced to improve the global search capability. The

simulation results show that the search efficiency is improved significantly by using this method.

1 INTRODUCTION

Swarm robotic (SR) research is inspired by the group

behaviors of bees, birds and other groups. A single

robot is thought to be unintelligent, but it can achieve

the desired goal through group behaviors and

demonstrate intelligence. The concept of swarm

robotics was first proposed by G. Beni et.al. Swarm

intelligence studies are devoted to simulating swarm

intelligence of natural organisms, which is to enable

individuals with simple perception to emerge swarm

intelligence through local communication. The

characteristics of swarm robotics: (1) the robot has

independent perception and communication ability.

(2) the robot has simple ability and low cost. (3) the

robot is independent of each other, and the structure

is distributed. (4) the self-organization ability based

on local communication (Şahin, E. 2004; Balch, T.

2004; Xue, S.,2008; Zeng, 2010; Zhuang, 2013)

Target search is one of the benchmark problems

in swarm robotics. Robots can perform tasks that

humans can't accomplish or are extremely dangerous

at low cost and price with the application of swarm

intelligence. For example, exploration, mine

sweeping, battlefield search, search and rescue in

hazardous areas, etc. In view of the fact that particle

swarm optimization uses individual effective

information and local communication to influence the

neighborhood individuals moving toward local

optimum, Doctor. s et.al. (2004) introduce Particle

Swarm Optimization (PSO) algorithm into multi

robot search system. Aiming at the characteristics of

dynamic neighborhood and limited communication

range in multi robot search, Pugh et.al. (2006)

improved the problem model and formed a classical

swarm robotic target search model. Anh-Quy H et.al.

(Zhang, 2014) analyzed and compared the effects of

two improved particle swarm algorithms in the

exploration of unknown environments. The paper

mainly improved the missing and collision problems.

Based on the model of swarm robotic search problem

proposed by Doctor. S et.al. (2004) and Pugh et.al.

(2006), Zhang et.al. (2014) proposed a model that

robots search targets cooperatively in the unknown

environment. In this model, the distributed robot has

a single perception ability, and has the ability of self-

localization and local information interaction. This

model fits the characteristics of swarm intelligence

and is representative. However, the search efficiency

of swarm robotics in the random search stage is not

achieved, especially when the target location is

remote, which slows down the overall search process.

The improved particle swarm optimization with

artificial potential field has achieved good results in

solving the problem of loss and collision (Hoang,

2016). In order to solve the problem that the

exploration range is too concentrated and the remote

area is easy to miss when the robot performs the

unknown environment exploration task. In this paper,

the artificial potential field improved spiral search

method is used to drive other roaming robots to other

unexplored regions. Through this improvement, the

476

Lu, S. and Hao, Y.

An Evaluation of Swarm Robotic Cooperative Target Search.

In 3rd International Conference on Electromechanical Control Technology and Transportation (ICECTT 2018), pages 476-486

ISBN: 978-989-758-312-4

target in the unknown position can get the attention of

the search robot earlier. Thus, the robot can detect

unknown targets as soon as possible. Simulation

results show that the search time of roaming stage is

reduced.

The cooperative search of swarm robotics can be

divided into three steps. The first step is roaming

search. The second step is to obtain local search

information through neighborhood communication,

and then determine their respective targets to search.

The third step is that robots with the same goal form

search alliances, and then search their targets

precisely by particle swarm optimization. The

traditional particle swarm optimization algorithm

guides the robots to the position of the local optimal

positions and their optimal positions. Inspired by

localization technology, directional technology is

introduced into particle swarm optimization. The

directional results are used to guide the robots to

approach the most likely positions of the targets.

Based on the proposed roaming strategy, a particle

swarm optimization algorithm based on auxiliary

orientation technology is proposed. Simulation

results show that the algorithm improves the

efficiency of swarm robotic search.

2 PROBLEM DESCRIPTION

2.1 Description of environment and

system

The robot starts from a random location of the search

environment to search for the task target in the

environment space. It is assumed that the robot can

locate itself (Pugh, 2006) in a certain positioning

mechanism and obtain its own position relative to the

environment. Only based on these can the robot

acquire and update its best position and share the best

position with other robots in the neighborhood. Then,

the local optimal location in neighborhood is obtained

by comparison. Finally, the particle swarm algorithm

is used to approach and locate the target.

Four tuple <R, E, T, S> can be used to describe

the multi objective search problem of swarm robots

(Kennedy, 2002):

a. Search agents (R): R=<U, B, C>;

R refers to a single robot. U is a collection of

objects directly detected by the robot and indirectly

obtained by interacting with the robots in the

neighborhood. B is the autonomous decision-making

behavior of the robot, that is, according to its own

perception of the environment and information

indirectly obtained, the robot autonomously

determines its own search mode; C represents the

cooperation of robots on the basis of neighborhood

communication;

b. Targets (T): T = {

T , i = 1 ... M}, m > 1;

T are the targets of swarm robots, that is, the task

set to be searched. Each target has its own signal

frequency, which is used to distinguish different

targets. M is the number of targets in a task.

c. Swarm robot (S): S = {

, j=1 ... n} n> >m;

S is a collection of all robots participating in the

search task. N is the total number of robots.

d. search environment (E): two-dimensional space

in closed space

2.2 Robot

N autonomous robots, as search subjects, constitute

swarm robots, which are robots with limited detection

distance, positioning accuracy, communication range

and so on (Zhang, 2015). The detector configured by

the robot can detect the signal emitted by the target

and obtain the intensity information. However, the

detection radius of the robot detector is relatively

small compared with the environmental dimension.

Based on the detected target intensity information

and neighborhood information, each robot switches

between three working modes: roaming mode,

particle swarm search mode, and capturing target

mode (Liu, 2010). When the robot does not obtain the

target information directly or indirectly, the roaming

mode is adopted. When the robot senses the target

directly or indirectly, and decides to take part in the

local search, the particle swarm search model is

adopted. Moreover, the robot continuously exchanges

the latest position and intensity information with

other robots in the communication neighborhood.

When the signal intensity directly detected by the

robot reaches the standard, the robot enters the

capturing target mode and announces the target to be

searched through neighborhood communication.

Then the robot continues to participate in the search

for the remaining target until all the targets are

searched.

2.3 Communication neighborhood and

distributed control

In the standard particle swarm optimization

algorithm, the neighborhood of the particle is the

whole search space. The particle can exchange

information with particles at any position in the

search space. In the swarm robotic system,

considering the communication distance and ability

An Evaluation of Swarm Robotic Cooperative Target Search

477

of a single robot is bound to be limited, the

communication distance must be greater than the

detection distance, but it should be smaller than the

environmental size. Otherwise, the robot will have

global communication capability. In our model, the

neighborhood of each robot is defined as the region

within its maximum communication distance. The

neighborhood is dynamic with time, because the

robot is moving continuously (Pugh, 2007). The robot

exchanges its own position and detected signal

intensity with other robots in the neighborhood.

Distributed control requires less communication

distance and capability, and does not require a robot

with central processor function. Full distributed

control is an important feature of swarm robotics.

2.4 Signal intensity

In particle swarm optimization, the local optimum

positions and the optimal locations of individuals are

determined by the intensity of the perceived signals.

Suppose each robot is equipped with a signal detector,

which can detect the intensity of different frequency

signals emitted by different targets. Xue et.al. (2008)

made a detailed analysis of the signal. The signal

intensity model of this paper is Eq.1 (Pugh, 2007):

/()

IPd





(1)

P is the power of the signal source. d is the

Euclidean distance between the robot and the signal

source.



is a random disturbance. Assuming that the

detection threshold is

, then

max

()

IIR

. If the

distance between the robot and the target exceeds the

maximum detection radius of

max

R , the target signal

cannot be detected.

2.5 Collision problem and speed limit

Particles are assumed to be infinitely small in particle

swarm algorithms, so they cannot conflict with each

other. But in the robot cooperative search system,

both the robot and the target have their own geometric

dimensions, so the collision problem needs to be

considered. Pugh et.al. (2007) adopts the Braitenberg

obstacle avoidance method, which is that the robot

will continue to select the previous motion speed after

changing direction. The obstacle avoidance method

proposed by Liu et.al. (2012) requires the current

state of motion of each robot and the speed at the next

moment. It is difficult to apply for robot with limited

detection ability and accuracy. Anh et.al. applies the

artificial potential field method to particle swarm

optimization to solve the problems of disconnection

and collision in multi-robot target search (Hoang,

2016). This paper uses the same method to solve the

obstacle avoidance problem in particle swarm

optimization.

The particles in the basic particle swarm

optimization algorithm have no acceleration and

speed constraints, but the speed of the robot is limited

in reality. If the speed of the robot obtained by particle

swarm algorithm exceeds the maximum, the speed

will be set to the maximum value. Only in this way

can the collision problem be handled at each step and

the robot can avoid crossing each other. Furthermore,

in order to make each step of the robot not seem to be

done in a flash. The moving distance of the robot in

each loop is divided into several segments to make its

moving trajectory smoother.

2.6 Division of tasks

One of the most commonly used methods of task

assignment is market based strategy (Dias, 2006). It

is not suitable to adopt the market based strategy in

swarm robotic system. The decomposition of the

tasks is accomplished by the robots autonomously in

the framework of swarm robotic system (Liu, L.,

2012). The global division of tasks is completed after

each robot decides its own goal. Therefore, the most

commonly used method of division in swarm robot

system is the method based on threshold (Zhang,

2014). This paper adopts the method based on

threshold to divide the tasks.

2.7 Adjustment of division

The target detected first will take the attention of

much more robots. It is possible all the robots that

have detected the target will take the target as their

goals, if we do not introduce the adjustment of task

selection. Which will cause local crowding and waste

the resources of system. Furthermore, it will reduce

the efficiency of global search.

Based on the intensities of the objective signal

detected by the robots. We rank the robots those

choose to search the same target. Zhang et.al. (2014)

point out that the ideal search efficiency can be

achieved by setting the maximum number of robots

to six in an alliance. The alliance is composed of the

robots with the same target to search. Only the top six

robots can join in the alliance, while there are more

than six robots choose the same target. The other

robots should convert to roaming mode. On the other

hand, while there are less than six robots choose the

same target, all these robots can join in the alliance.

ICECTT 2018 - 3rd International Conference on Electromechanical Control Technology and Transportation

478

Furthermore, we adopt the mechanisms of exit and

punishment (Zhang, 2014).

3 APE IMPROVED SPIRAL

ROAMING STRATEGY

3.1 APE

Proposed by Khatib.O in 1986 for single robot path

planning (Kennedy, 2002), APF is now widely used

in works on multi-robot system. APF generates

around each robot a virtual potential field containing

a repulsive field and an attractive field. The attractive

field directs each robot towards other robots in the

system while the repulsive field keeps them far away

from other robots or obstacles. The magnitude of

potential forces exerted on each robot are

continuously updated based on the information it gets

from the immediate surrounding environment, or

from other robots via connection network (Hoang,

2016).

3.2 Spiral roaming strategy

The size of the space to be explored is much larger

than the maximum detection distance of the detector

configured by the robot. When the search begins, the

robot first enters the random wandering state to find

the target signal (Xue, 2009). In order to cover as

much space as possible in the shortest time, we can

adopt the spiral roaming strategy mentioned by AT

Hayes (2002), and the explosion dispersing roaming

strategy proposed by Meng et.al. (2008). In view of

the fact that the explosive dispersion roaming strategy

may be too dispersed in the long distance, and then

the blind zone appears, the spiral roaming strategy is

adopted in this paper. The spiral can be realized by

Eq.2.

cos( / 4 )

sin( / 4 )

vt wt

yvt wt



  





  



(2)

Where, x and y are the coordinates of the points

on the spiral, t is the time variable, v is the linear

velocity, w is angular velocity,



is the initial

angle. The divergence of the spiral can be controlled

by controlling those parameters.

3.3 APE-Spiral Roam

In the simulation of (Liu, 2010; Xue, 2009) or in this

paper, in the original spiral roaming state, the robot

search paths are close to each other, and do not play

the proper efficiency of multiple robots. The

efficiency of swarm robotic search has been greatly

affected. At this point, the machines appear to be

unintelligent, and on the contrary, when people

cooperate to find the target, they will inform the

people within the scope of communication "there is

no target here.

It is not a new idea to applying APF to multi-robot

system. However, in previous works, they are only

used for formation control and path planning (Hoang,

2016; Pugh, 2006; Liu, 2012). Furthermore, Anh-Quy

H et.al. (2016) use APE for the task of space

exploration. To solve the problem mentioned above,

we use artificial potential field to simulate human

communication, that is to tell the surrounding robot,

search elsewhere. Thus, the original spiral roaming

strategy is improved.

Figure 1: Potential field.

The potential field of each robot is shown in Fig.1,

with the center of the position of each robot as the

center of the circle, and three circular regions with

radius of

R ,

R and

R are established

respectively.

In the figure,

R is the center of the robot.

R is

the radius of attractive field. The robots are attracted

by the robot at

R when they are between

R and

. Between

R and

R , the robots are not affected by

the robots at

R in this area.

R is the radius of the

repulsive field, and the robots are repulsed by the

robot at

R when they are in the repulsive field.

Under the combined action of attractive field and

An Evaluation of Swarm Robotic Cooperative Target Search

479

repulsive field. It avoids the gaps between the robots

become the blind area of the detection, and also

prevents the robot from penetrating into the detection

area of other robots. After introducing the concept

mentioned above. We let the roaming robot adopt the

spiral roaming strategy. This is called the Ape-Spiral

Roam method. To illustrate this method, the

following Eq.3 is introduced:

12 12 12 1 12 2

12 3

[u(r ) u(r r ) ku(r r )

ku(r r )] 3

APE

Gm m

 



（

）

1, 0

()

0, 0













(4)

G is the gravitational constant in the formula, and

k is the adjustment factor.

m and

m represent the

reliability values of robots.

R is the distance vector

from robot 1 to robot 2.

is the force of robot 1

acting on robot 2. The combinative force of other

robots under robot j is calculated by Eq.5:

APEj AP





(5)

The combinative force gives an additional

acceleration component to each robot. The velocity of

each robot is calculated by Eq.6:

 

1= +

i i APEi

vt vt v t

(6)

4 AO IMPROVED PSO

4.1 Premature convergence of PSO

PSO algorithm shows good performance in multi-

target search. But in the traditional particle swarm

algorithm, in the later stage of the search process,

after several cycles, the particles are likely to follow

the local optimal particles to fly. Thus, the ability of

individual exploration decreases and premature

convergence occurs.

Similarly, the location of the local optimal robot

is not the location of the target in multi-target search

system. Premature convergence is also easy to

happen. It is better to direct robots to the potential

target position than to direct robots to the optimal

position in the neighborhood.

4.2 Auxiliary orientation technology

Inspired by localization technology, directional

technology is introduced into particle swarm

optimization. Before the premature convergence

occurs, the position of the target is estimated by using

the robot which satisfies the distance between each

other by local communication. The estimated position

is introduced into particle swarm optimization to

improve the searching ability of PSO.

The signal intensity perceived by the optimal

robot is directly related to the distance between the

robot and the signal source. The signal intensity can

be used to estimate the distance between the signal

source and the local optimal robot by Eq.7. Where i

is the number of the robot. It can be inferred that the

signal source is in a circular orbit around the local

optimum robot, whose radius is the estimated

distance.

d| /I|

P (7)

If there is another robot directly detects the same

source. We can find the distance between the second

robot and the signal source in the same way. The

signal source is also in a circular orbit around the

robot, whose radius is the estimated distance.

Suppose the coordinates of two robots are

1, 1

()

and

2, 2

()

. Then two intersection points can be obtained

by solving the system of Eq.8 formed by two circles.

222

111

222

()()

()( )

xyyd















(8)

Suppose the coordinates of two intersection points

are

1, 1

()

and

2, 2

()

. The coordinates of the third

robot are

3, 3

()

. And

d is the distance between the

third robot and the signal source. Find the distances

between third robot relative to the two intersections

by Eq.9.

33 3

()()

ii i

dxsyz

(9)

As the follow Eq.10. If the two distances are not

equal. The distance which is closer to

d is used to

inferred the position of the signal source. And h is the

adjustable constant to avoid the mistake choice. In

this paper we select h=10.

ICECTT 2018 - 3rd International Conference on Electromechanical Control Technology and Transportation

480

33 3 3

33 33

(, ),| | | |

ii i j

jj j i

zddhdd

 









 





(10)

Where

is the estimation position of the signal

source. Which is introduced into particle swarm

optimization by Eq.11.

,,, , ,,

,,, ,

( ) () ( - ) ( - )( - ) ( - ) ( - ) 3

(1)

( ) () ( - ) () ( - )

ij p ij ij n fs ij n fs sz ij d

ij p ij ij n ij

w v t w rand x x w u L d x x w d L x x N

w v t w rand x x w rand x x



     



    3













(11)

1, 0

()

0, 0















(12)

Where

is the distance from the first robot to

the second robot that detect the same target. L is the

adjustable factor to avoid the second robot being too

close to the first robot. In this paper we select L=20.

represent the number of robots that detect the

same target directly.

(t)



is the unit step function,

,ij



is the best position of the individual robot,

,ij



is the best position of the sub-swarm robots. w is the

weight of inertia,

is the weight of the best

position of the individual,

w is the weight of local

best position.

,,,

(1) () ()

ij ij ij

txtvt 

(13)

The position of every robots is calculated by

Eq.13. This algorithm is called auxiliary orientation

technology improved Particle swarm optimization

algorithm (AO-PSO).

4.3 Extension of Directional technology

In the early stage of particle swarm algorithm, there

is only one robot that detects the target directly.

Inspired by the characteristics of directional Yagi

antenna. The position information and the target

intensity information of the robot which uniquely

detects the target are stored. The early position of the

target is estimated by the position information and

intensity information of a single robot in the scattered

position. Using the estimated location information to

direct other robots to detect the target as early as

possible.

5 SIMULATION AND RESULTS

In order to evaluate the effectiveness of the algorithm,

visual simulation was performed under Matlab. Two

groups of experiments were carried out under two

conditions. According to the different experimental

purposes, various parameters were changed and

repeated experiments were carried out. The

experimental results are analyzed and compared with

the existing methods, and the statistical results are

obtained.

5.1 Parameters and conditions

The main parameters of the simulation include

subject, object, environment, etc. The parameters are

shown in Table 1.

The initial position of each robot is randomly

generated in the range of 20 to 120 from the starting

point. The initial velocity of the robot is randomly

generated between 1 and 5, and the direction is

random. The target is generated at a random location

at a certain distance from the starting point.

An Evaluation of Swarm Robotic Cooperative Target Search

481

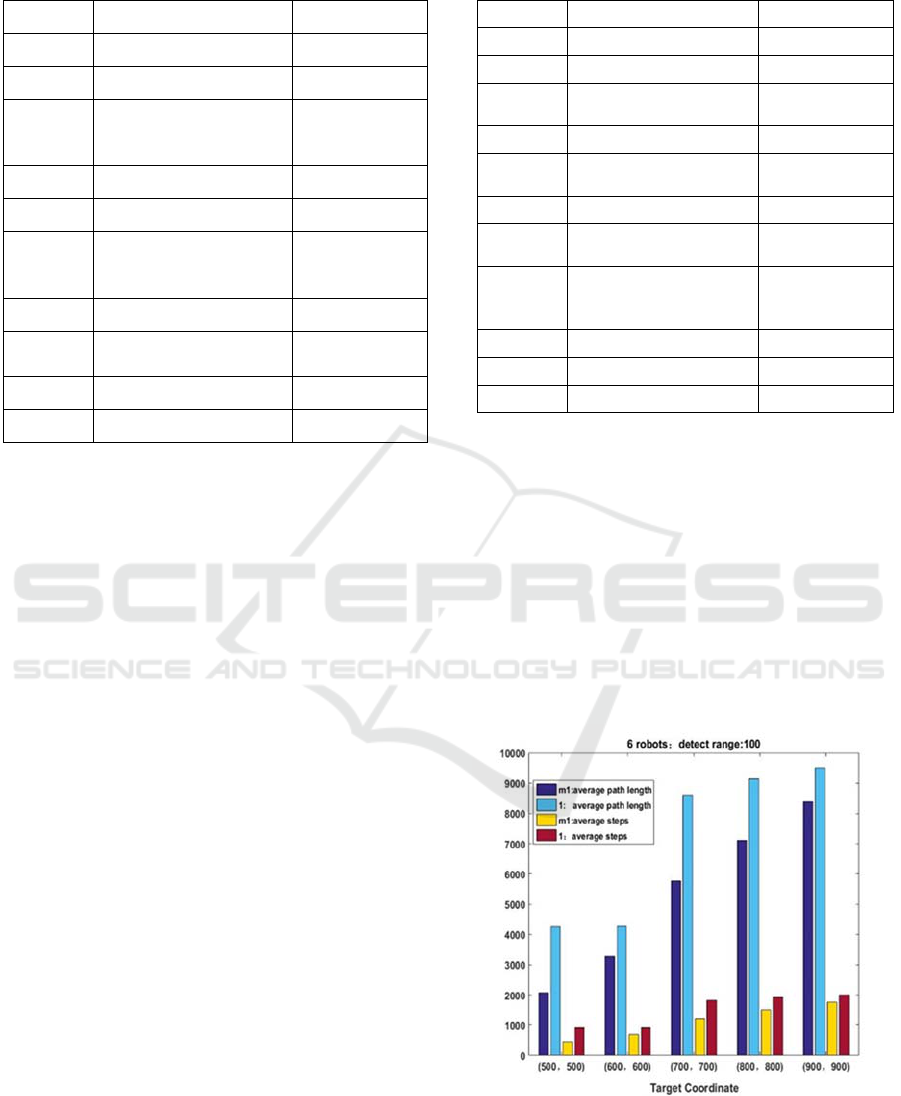
Table 1: Parameter settings for simulation.

Symbol Meaning Value

Nrob Number of robots 6-100

D Number of targets 1-12

E Size of environment

1000*1000-

2000*2000

Rmax Detection distance 100-200

Rcom Communication radius 300

The power of the signal

emitted by the target

1000

λ gain 10

Nmax

Upper limit of alliance

size

T Maximum time 2000

Vmax Maximum speed 5

5.2 Experiment 1

In the first set of experiments. In order to facilitate the

comparison, the swarm robotic search method in

paper (Liu, 2010) is called algorithm 1, and the

method after using the improved roaming strategy of

APE in this paper is algorithm M1.

In order to highlight the difference of search

efficiency between two algorithms in roaming stage,

the algorithm stops when the roaming algorithm gets

the initial position of the target. What enhances the

alignment of the experiment and highlights the effect

of the improved roaming algorithm.

The starting point of robot is fixed near the

coordinate origin, and the position of target is

changed continuously. This enhances the adaptability

of the model and is more suitable for the search model

in unknown environments. The number of robots is

adjusted to 6 and 12, and the number of targets is

adjusted to 1. Environment size, maximum detection

distance, and other parameters are shown in Table 2.

Table 2: Parameter settings for Experiment 1.

Symbol Meaning Value

Nrob Number of robots 6-12

D Number of targets 1

E Size of environment

1000*1000-

2000*2000

Rmax Detection distance 100-150

Radius of attraction

force

300

R2 Radius of stable region 280

Radius of repulsive

force

180

The power of the

signal emitted by the

target

1000

λ gain 10

T Maximum time 2000

Vmax Maximum speed 5

Performance criteria: the probability of

completing tasks, the average steps required to

complete the task, the average path length, the

scalability of the system scale, the adaptability of the

environmental scale, and the adaptability of the

detection range.

In each case, we have done 120 repetitions. Then

the average of the results is calculated. The

probability of the two algorithms to complete the task

is one hundred percent. The comparison of other data

is shown in Fig.2 to Fig.5.

Figure 2: For 6 robots with the detect range of 100.

ICECTT 2018 - 3rd International Conference on Electromechanical Control Technology and Transportation

482

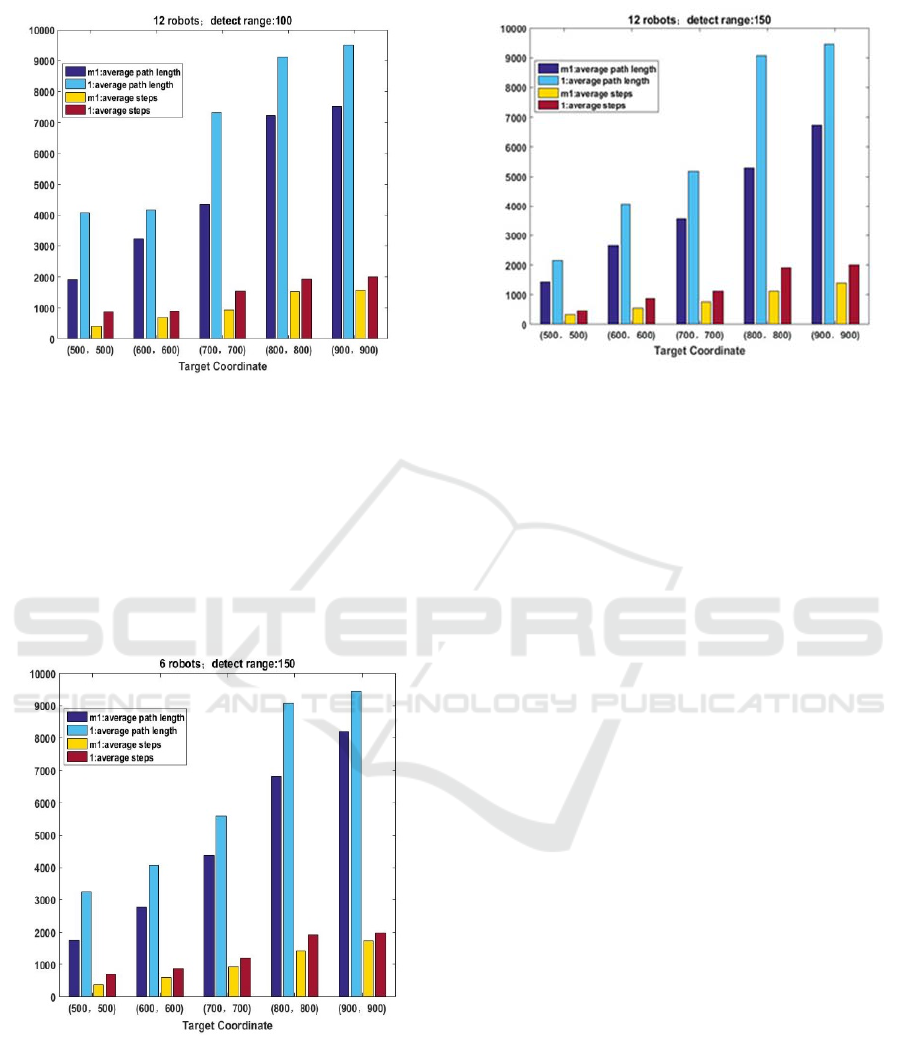
Figure 3: For 12 robots with the detect range of 100.

We can see from Fig.2 and Fig.3 In aspect of

system size, the number of robots in the system

increased from 6 to 12. In aspect of environmental

scale adaptation, the position of the target varies from

(500,500) to (900,900). Compared with the algorithm

1, the algorithm M1 has significant improvement in

two aspects: the average steps required to complete

the task and the average length of the path to complete

the task.

Figure 4: For 6 robots with the detect range of 150.

Figure 5: For 12 robots with the detect range of 150.

Compared with Fig.2 and Fig.3, the detection

distances in Fig.4 and Fig.5 are increased from 100 to

150. Compared with algorithm 1, the algorithm M1

still has significant improvement in two aspects: the

average steps required to complete the task and the

average length of the path to complete the task. Thus,

the advantages of the algorithm M1 are verified in the

detection range adaptation.

In summary, the APE improved roaming strategy

proposed in this paper has obvious effect in

improving the search efficiency of roaming stage.

5.3 Experiment 2

In the second experiment, the particle swarm

optimization algorithm in the literature (Zhang,

2014) is called algorithm 2, and the AO-PSO

algorithm is called algorithm M2.

In order to emphasize the difference between the

two algorithms in the particle swarm search stage, the

roaming stage is not improved. In order to compare

the efficiency of particle swarm optimization after the

improvement of AO-PSO, and enhance the contrast

effect, the maximum detection distance is expanded

to 250. Other parameters such as the size of the

environment, the number of robots, the number of

targets, etc. are shown in Table 3.

An Evaluation of Swarm Robotic Cooperative Target Search

483

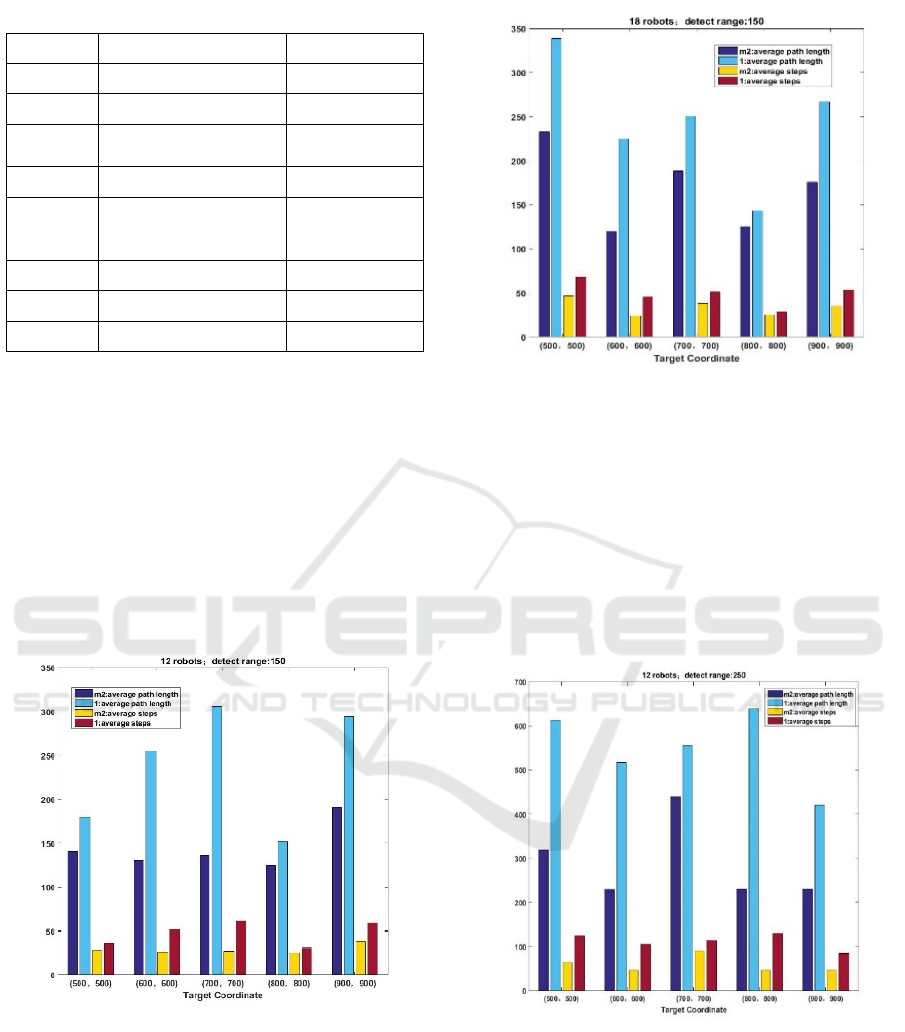
Table 3: Parameter settings for Experiment 2.

Symbol Meaning Value

Nrob Number of robots 12-18

D Number of targets 1

E Size of environment

1000*1000-

2000*2000

Rmax Detection distance 150-250

The power of the

signal emitted by the

tar

1000

λ gain 10

T Maximum time 2000

Vmax Maximum speed 5

Performance criteria: the probability of

completing tasks, the average steps required to

complete the task, the average path length, the

scalability of the system scale, the adaptability of the

environmental scale, and the adaptability of the

detection range.

In each case, we have done 120 repetitions. Then

the average of the results is calculated. The

probability of the two algorithms to complete the task

is one hundred percent. The comparison of other data

is shown in Fig.6 to Fig.9.

Figure 6: For 12 robots with the detect range of 150.

Figure 7: For 18 robots with the detect range of 150.

We can see from Fig.6 and Fig.7. In the aspect of

system size, the number of robots in the system

increased from 12 to 18. In the aspect of

environmental scale adaptation, the target position

varies from (500,500) to (900,900). Compared with

the algorithm 2, the algorithm M2 has significant

improvement in two aspects: the average steps

required to complete the task and the average length

of the path to complete the task.

Figure 8: For 12 robots with the detect range of 250.

ICECTT 2018 - 3rd International Conference on Electromechanical Control Technology and Transportation

484

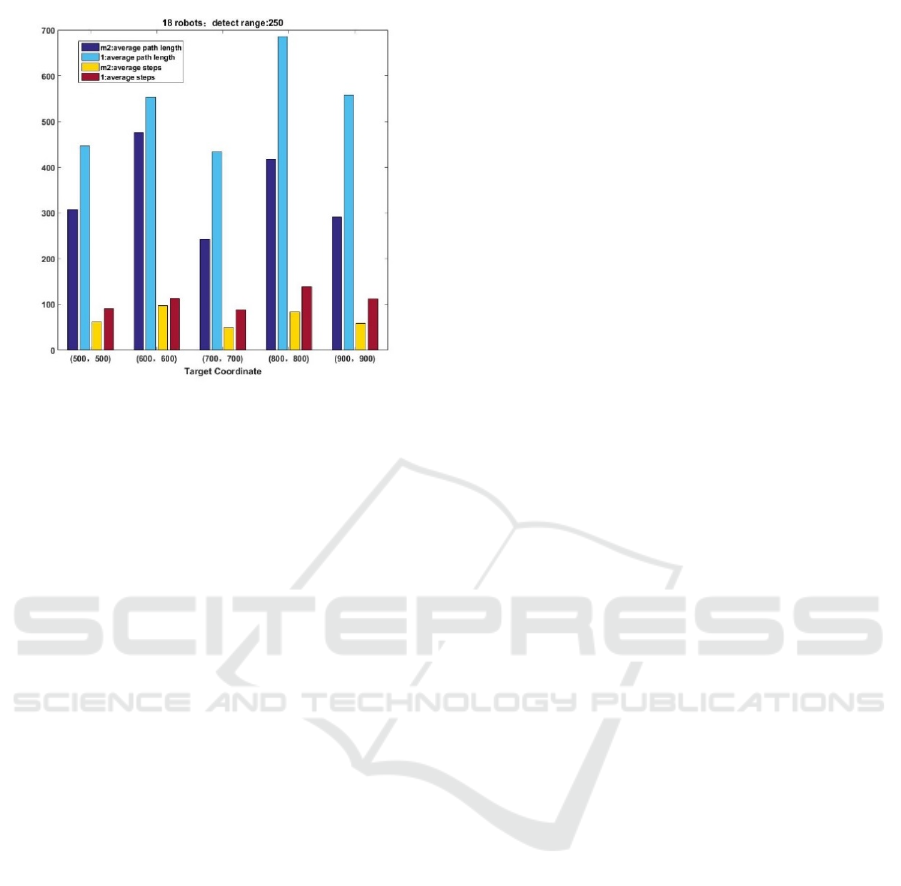
Figure 9: For 18 robots with the detect range of 250.

Compared with Fig.6 and Fig.7, the detection

distances in Fig.8 and Fig.9 are increased from 150 to

250. Compared with algorithm 2, the algorithm M2

still has significant improvement in two aspects: the

average steps required to complete the task and the

average length of the path to complete the task. Thus,

the advantage of the algorithm M2 has the

adaptability of detection range.

In summary, the AO-PSO algorithm proposed in

this paper has obvious effect in improving the

efficiency of particle swarm optimization search

stage.

6 CONCLUSIONS

In this paper, we propose algorithm M1 and algorithm

M2. Two algorithms are used to solve the problem of

comprehensive efficiency in swarm robotic search.

The simulation results show that the algorithm M1

and the algorithm M2 maintain good environment,

system scale, and detection distance fitness. In the

case of the same completion rate, the two improved

algorithms have greatly improved the search

efficiency compared with the original method.

Compared with the algorithm 1, through the

improvement of the M1 algorithm, the time and the

average path to find the approximate location of the

target in the roaming phase are reduced. It effectively

improves the search efficiency of the roaming phase

in swarm robotic search. Compared with the

algorithm 2, the improvement of M2 algorithm

reduces the time consuming and average path of

collaborative search stage, and improves the search

efficiency in the collaborative search phase.

REFERENCES

Şahin, E. (2004). Swarm Robotics: From Sources of

Inspiration to Domains of Application. International

Conference on Swarm Robotics (Vol.3342, pp.10-20).

Springer-Verlag.

Balch, T. (2004). Communication, Diversity and Learning:

Cornerstones of Swarm Behavior. International

Conference on Swarm Robotics (Vol.3342, pp.21-30).

Springer-Verlag.

Xue, S., & Zeng, J. (2008). Swarm Robotics: A Survey. PR

& Al, 21(2), 177-185.

Zeng, J, & Xue, S. (2010). Modeling and Simulation

Approaches to Swarm Robotic Systems. Journal of

System Simulation, 22(6), 1327-1330.

Zhuang, Q. (2013). Prototype system design for

coordinated control research of swarm robotics.

(Doctoral dissertation, Taiyuan University of Science

and Technology).

Doctor, S., Venayagamoorthy, G. K., & Gudise, V. G.

(2004). Optimal PSO for collective robotic search

applications. Evolutionary Computation, 2004.

CEC2004. Congress on (Vol.2, pp.1390-1395 Vol.2).

IEEE.

Pugh, J., & Martinoli, A. (2006). Applying aspects of multi-

robot search to particle swarm optimization.

International Workshop on Ant Colony Optimization

and Swarm Intelligence (Vol.4150, pp.506-507).

Springer Berlin Heidelberg.

Zhang, Y., Xue, S., & Zeng, J. (2014). Dynamic Task

Allocation with Closed-Loop Adjusting in Swarm

Robotic Search for Multiple Targets. Robot, 36(1), 57-

68.

Hoang, A. Q., & Pham, M. T. (2016). Comparing modified

pso algorithms for mrs in unknown environment

exploration.

Pugh, J., & Martinoli, A. (2006). Relative localization and

communication module for small-scale multi-robot

systems. IEEE International Conference on Robotics

and Automation (pp.188-193). IEEE.

Kennedy, J., & Eberhart, R. (2002). Particle swarm

optimization. IEEE International Conference on Neural

Networks, 1995. Proceedings (Vol.4, pp.1942-1948

vol.4). IEEE.

Zhang, Y., Xue, S., & Zeng, J. (2015). Cooperative and

Competitive Coordination in Swarm Robotic Search for

Multiple Targets. Robot, 37(2), 142-151.

Liu, Z., Xue, S., Zeng, J., Jing, Z., & Zhang, G. (2010). An

evaluation of PSO-type swarm robotic search:

Modeling method and controlling properties.

International Conference on Networking, Sensing and

Control (pp.360-365). IEEE.

Pugh, J., & Martinoli, A. (2007). Inspiring and Modeling

Multi-Robot Search with Particle Swarm Optimization.

An Evaluation of Swarm Robotic Cooperative Target Search

485

Swarm Intelligence Symposium, 2007. Sis (Vol.51,

pp.332-339). IEEE.

Xue, S. D., & Zeng, J. C. (2008). Control over swarm robots

search with swarm intelligence principles. Journal of

System Simulation, 20(13), 3449-3454.

Liu, F., Narayanan, A., & Bai, Q. (2012). Effective methods

for generating collision free paths for multiple robots

based on collision type (demonstration). International

Conference on Autonomous Agents and Multiagent

Systems (pp.1459-1460). International Foundation for

Autonomous Agents and Multiagent Systems.

Dias, M. B., Zlot, R., Kalra, N., & Stentz, A. (2006).

Market-based multirobot coordination: a survey and

analysis. Proceedings of the IEEE, 94(7), 1257-1270.

Liu, L., & Shell, D. A. (2012). Large-scale multi-robot task

allocation via dynamic partitioning and distribution.

Autonomous Robots, 33(3), 291-307.

Zhang, G., & Zeng, J. (2011). Area Coverage Algorithm

in Swarm Robotics Based on Wasp Swarm Algorithm.

PR & Al, 24(3), 431-437.

Xue, S. D. (2009). Swarm Robotic Search for Target:

Cooperative Control Techniques, Strategies, and

Simulations. (Doctoral dissertation, Lanzhou

University of Technology).

Hayes, A. T. (2002). Self-organized robotic system design

and autonomous odor localization. California Institute

of Technology.

Meng, Q., Li, F., Zhang, M., Zeng, M., & Wei, X. (2008).

Study on Realization Method of Multi-Robot Active

Olfaction in Turbulent Plume Environments. ACTA

AUTOMATICA SINCA, 34(10), 1281-1290.

ICECTT 2018 - 3rd International Conference on Electromechanical Control Technology and Transportation

486