
A Gravity-Compensation Algorithm for the Haptic Device Based on
the Principle of Virtual Work and BP Neural Network
Shuo Wang, Zhiyuan Yan, Zhengxin Yang
and Zhijiang Du
*
State Key Laboratory of Robotics and System, Harbin Institute of Technology, Xidazhi Street, Harbin, China
*
hitwangshuo@foxmail.com
Keywords: Haptic device, Gravity-compensation, Principle of virtual work, BP neural network.
Abstract: The haptic device is the key facility in the master-slave minimally invasive surgery system, a gravity-
compensation algorithm is proposed for this device. The structure of this device mentioned in this paper is a
combination of serial and parallel structure, and it has 6 degrees of freedom. 3 motors are installed at 3 active
joints respectively. In order to establish the dynamic equation of the haptic device, the device is simplified
and the torque which is used to compensate the gravity is calculated by the principle of virtual work (Codourey
A, 1998). Then the whole process of gravity-compensation is simulated under the environment of a dynamic
software. After the comparison between the theoretical model and the simulation result, errors are shown and
compensated through BP neural network, the performance of the gravity-compensation is improved.
1 INTRODUCTION
The master-slave minimally invasive surgery system
has been widely used, it has numbers of advantages
and they are recognized by the public (Okamura A M,
2011). The haptic device is very important in the
whole system for the surgeon relies on it to feel the
feedback force. The haptic device should not only
meets the needs of high stiffness, low damping and
small inertia, but also be able to compensate its own
gravity (Wang and Gosselin, 1998). The methods
which can realize gravity-compensation can be
classified as mechanical method and dynamic
method. Mechanical methods mainly include
counterweight method, equivalent mass method and
spring compensation method (Zhang L N, 2013);
dynamic methods mainly contain Newton-Euler
method, virtual work method and Lagrange method
(You W, 2008).
In order to simplify the modelling process, the
principle of virtual work is used to establish the
dynamic model, it provides a theoretical basis for
gravity-compensation. Then the haptic device is
simulated by relative software and the simulation
torque is obtained. After comparing the theoretical
torque and simulation torque, errors are found. Then
BP neural network is used to compensate the errors
(Wu B, 2016).
2 HAPTIC DEVICE
The haptic device is made by the serial part and
parallel part, as shown in Figure 1. It has 6 degrees of
freedom, the parallel part has 3 degrees of freedom
which are used to control the position of the slave
device, the 3 degrees of freedom in the serial part
controls the posture of the slave device. The gravity-
compensation mentioned in this paper is carried out
by the parallel part, and the gravity-compensation of
the serial part is not discussed.
Figure 1: The haptic device.
The parallel part consists of 3 parts, namely
moving platform, static platform and 3 identical
branches, they are shown in Figure 2. Each branch has
Wang, S., Yan, Z., Yang, Z. and Du, Z.
A Gravity-Compensation Algorithm for the Haptic Device Based on the Principle of Virtual Work and BP Neural Network.
In 3rd International Conference on Electromechanical Control Technology and Transportation (ICECTT 2018), pages 599-605
ISBN: 978-989-758-312-4
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
599

7 revolute pairs, the semi-disc works as the active
link, its joint works as the active joint, while the
parallelogram mechanism works as the passive link.
Figure 2: The parallel part.
3 GRAVITY-COMPENSATION
3.1 Simplification of mechanical model
Branches of the haptic device are made of hard
aluminum alloy which has low density and mass, so
their moment of inertia can be ignored. The mass of
each branch can be divided into two equal parts, one
is added to the joint of semi-disc, the other one is
added to the joint of the static platform. When we
analyse the parallel part we can simplify the serial
part as a whole and add its mass to the moving
platform. After simplification we name the new
moving platform as synthetic moving platform and
the new semi-disc as synthetic semi-disc mechanism.
The simplified model is shown in Figure 3.
Figure 3: The simplified model.
3.2 Establishment of mechanical model
This haptic device has 3 active motors, if we only take
gravity into consideration then the dynamic model
can be described as:
() (,) ()MC G
(1)
In the equation,
is the 3×1 order joint moment
vector,
M
is 3×3 order inertia matrix, C is
centrifugal force and coriolis force,
G is the 3×1
order gravity,
is the turning angle of the active
joints.
If there is external force in the system the
principle of virtual work can be described as:
1
[( ) ( ) ] 0
N
jjj jj
j
WFmar I
(2)
In the equation,
W
is the sum of virtual work,
j
F
is external force,
j
m
is the particle mass,
j
a
is
the particle acceleration,
j
r
is the virtual
displacement,
j
is the external torque,
I
is moment
of inertia,
is the angle acceleration and
is
virtual angle.
3.3 Establishment of dynamic equation
3.3.1 Analysis of the simplified model
Figure 4: The coordinate system of the simplified model.
In Figure 4, the direction of
'
'' '
j
Cj Cj Cj
CX Y Z
and
jj j
jCC C
CX Y Z relative to
OO O
OX Y Z
can be
described with
O
Cj
T
. The angle between branch
j
and
O
Y in plane
OO
YOZ is
2( 1)3
j
j
and
1, 2, 3j
,
j
C
is at the rotation center of the semi-
disc.
j
is the turning angle of semi-disc and the
clockwise direction is positive.
T
xyz
DDDD
and it is the position of the
moving platform. The branch length is a constant and
if
'
jj
kAD
, then we have:
ICECTT 2018 - 3rd International Conference on Electromechanical Control Technology and Transportation
600

''''
1
21
()
0sin
cos
00
O
jj Cjjjj
xj
O
yCj j
z
kADODTOCCA
DL
DTRL
D
(3)
1
1
cos
sin
0
xj
O
j
yCj jj jj
z
DL
kD TL De
D
(4)
0
TT
jj jj
kk kk
(5)
With equation (4) and (5) we have:
0
TT
jjjj
kDke
(6)
In the equations above we know that
1, 2, 3j
,
then we simplify equation (6) based on
DJ
:
1
111
222
333
00
00
00
TT
TT
TT
kke
Jk ke
kke
(7)
After simplifying the derivative of equation (6):
1
11
22
33
TT
TT
TT
kk
Dk kJQJ
kk
(8)
11 11
22 22
33 33
00
00
00
TT
TT
TT
ke ke
Qkeke
ke ke
(9)
Based on
DJ J
and equation (8):
1
11
22
33
TT
TT
TT
kk
J
kkJQ
kk
(10)
After simplification, the mass of the synthesized
moving platform can be described as:
3
2
s
cd l
mmm m
(11)
In this equation,
s
m is the mass of the synthesized
moving platform,
c
m is the mass of the serial part,
d
m is the mass of the original moving platform,
l
m
is the mass of a branch.
After simplification, the mass of the synthesized
semi-disc can be described as:
1
2
bh l
mm m
(12)
In this equation,
b
m is the mass of the synthesized
semi-disc,
h
m is the mass of the original semi-disc.
The vector of synthesized semi-disc‘s center of
mass can be described as:
1
2
1
2
hh ll
cm
hl
mr mr
R
mm
(13)
In this equation,
h
r
is the vector of the semi-disc‘s
center of mass relative to the semi-disc‘s rotation
center,
l
r
is the vector of the centralized mass of the
branch relative to the semi-disc‘s rotation center.
With Figure 5 they can also be described as:
cos sin 0
T
hjj
rh h
(14)
sin cos 0
T
ljj
rl l
(15)
Figure 5: Semi-disc and its branch.
The gravity torque of the synthesized semi-disc
can be described as:
1
()
2
O
cm Cj cm h l
TR m mg
(16)
In this equation
00
T
gg
.
A Gravity-Compensation Algorithm for the Haptic Device Based on the Principle of Virtual Work and BP Neural Network
601
The rotary inertia of the synthesized semi-disc can
be described as:
22
1
1
2
bhlo h l
I
IIImh mL
(17)
In this equation,
h
I
is the rotary inertia of the
original semi-disc,
l
I
is the rotary inertia of the
centralized mass of the branch,
o
I
is the rotary inertia
of the original semi-disc relative to the semi-disc’s
mass of center.
3.3.2 Derivation of dynamic equation
During operation, the synthesized moving platform is
mainly affected by gravity
g
F
and inertia force
a
F
.
Based on the principle of virtual work we have:
()()
gcm b a
I
(18)
TT
gg s
J
FJmg
(19)
TT
aa s
JF JmD
(20)
Equation (18) can also be described as:
TT
bs scm
IJmDJmg
(21)
In this equation,
123
T
is the driving
torque of three joints.
123
T
cm cm cm cm
is
the gravity torque of three synthesized semi-discs.
With
DJ J
it can also be described as:
()
TTT
bs s scm
IJJm JJm Jmg
(22)
Compare equation (1) and (21) we have:
()
T
bs
M
IJJm
(23)
(,)
T
s
CJJm
(24)
()
T
s
cm
GJmg
(25)
3.3.3 Simulation
After inputting the relative equation and the physical
parameters into MATLAB, the theoretical torque
curve could be obtained. After importing the model
into ADAMS and adjusting relative settings, we
measure the driving torque and collect the data in
Postprocessor, we name it as the simulation data.
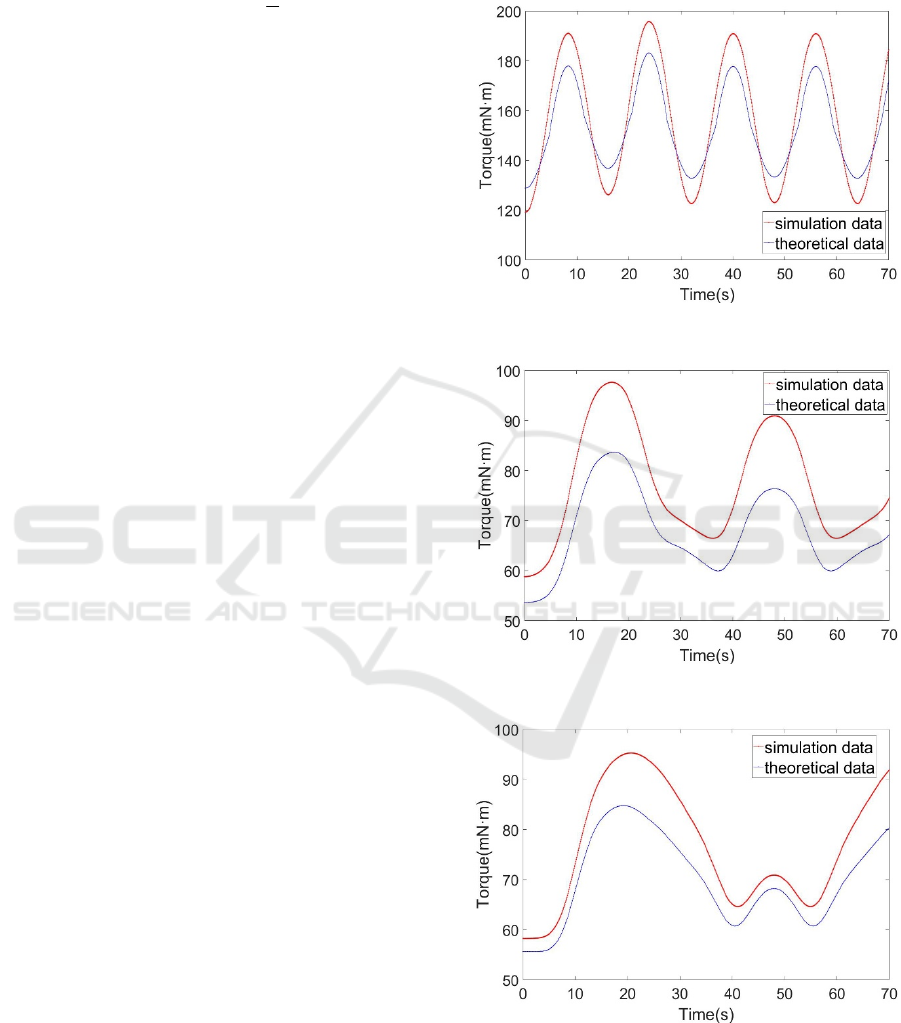
Figure 6: Simulation and theoretical torque of joint 1.
Figure 7: Simulation and theoretical torque of joint 2.
Figure 8: Simulation and theoretical torque of joint 3.
Although the theoretical data and the simulated
data show the same trend, the difference still exists.
The errors between the theoretical data and the
ICECTT 2018 - 3rd International Conference on Electromechanical Control Technology and Transportation
602
simulated data of the joints are shown in figure, the
standard deviation of these three pairs of curve are
9.768mN m , 9.854mN m and 7.44mN m .
4 GRAVITY-COMPENSATION
BASED ON BP NEURAL
NETWORK
The errors mentioned above mainly come from two
parts: the simplification of the model and the
ignorance of the friction. In order to improve the
result of gravity compensation, BP neural network is
used to compensate the errors.
BP neural network includes input layer, output
layer and hidden layers (Chu J, 2013). The connection
between different layers relies on the nodes, the
connection weights are different between different
node units, they reflect the strength between layers
and nodes is different (Li J, 2012). BP neural network
uses Widrow-Hoff learning algorithm and non-linear
transfer function. During the transfer process, the
information is transmitted in the positive direction
while the error is transmitted backwards. The
information enters the network through the input
layer, then it goes through the hidden layer and the
output layer (Ma C, 2016). During the whole process,
the output of the previous layer is the input of the next
layer. If the final output doesn’t meet the expectation,
then transmit the error backwards and adjust the
connection weights until the output meets the need.
The BP neural network used in this paper can be
described as:
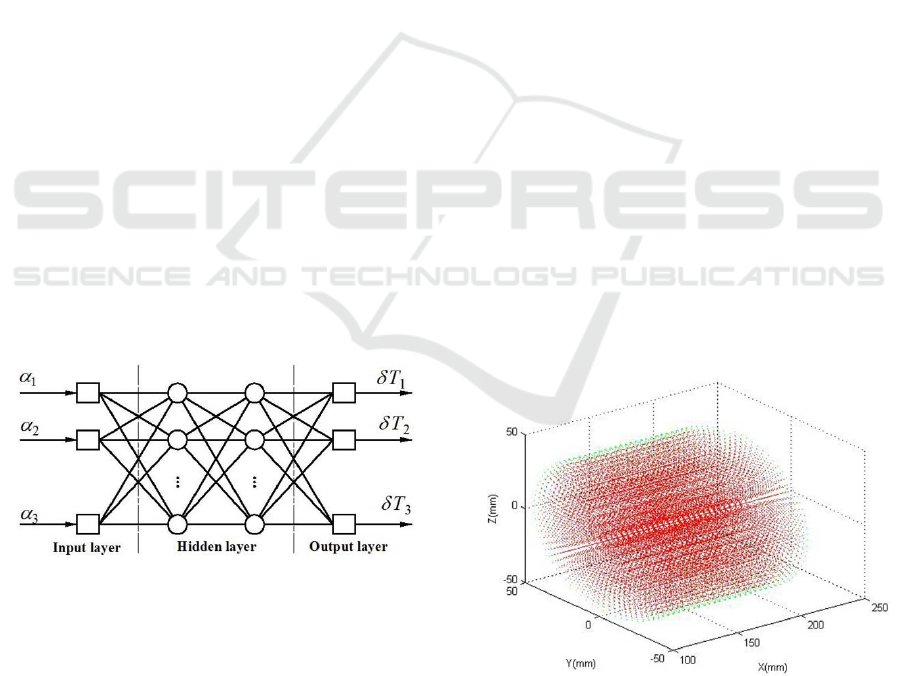
Figure 9: The structure of BP neural network.
The equation (22) can be changed as:
BP
T
(26)
In this equation,
B
P
is the driving torque, T
is
the output of the neural network, which is also the
compensated value of gravity compensation value.
Then we design the neural network for
T
, the
BP neural network used in this paper contains 4
layers, 2 hidden layers, 1 input layer and 1 output
layer. Set the activation function of the output layer
as the linear Purelin function and then set the
activation function of the hidden layers as non-linear
Tan-Sigmoid.
In this paper, we select the trainlm function as the
training method, it is based on Levenberg-Marquardt
algorithm. It is a kind of non-linear optimization
method between Newton's method and gradient
descent method, it can not only speed up the training
speed, but also reduce the possibility of falling into
the local minimum value. The design process is as
follows:
Firstly, we determine the input vector and the
expected response. Set the turning angle of the semi-
discs’ active joints
123
T
as input,
then set the errors between the driving torque and
theoretical torque
123
T
TTTT
as the
expected response, so the input and output layer both
have 3 node units.
Secondly, we determine the node number on the
hidden layers. We collected 28800 sets of sample data
and all of them are in the workspace of the haptic
device, it is shown in Figure 10. In the figure, green
points represent the workspace, while the red ones
represent the collected training data. In the training
process, the performance detection algorithm uses the
mean square error and it reaches its minimum value
3
1.5867 10
when the node number of the hidden
layers are 13 and 15. After the training, save the
neural network as a mat file.
Figure 10: The workspace of the haptic device.
Thirdly, we test the performance of BP neural
network. Collect 1024 sets of test data (all of the data
is in the workspace of the haptic device) in ADAMS,
and then calculate the error with the BP neural
A Gravity-Compensation Algorithm for the Haptic Device Based on the Principle of Virtual Work and BP Neural Network
603
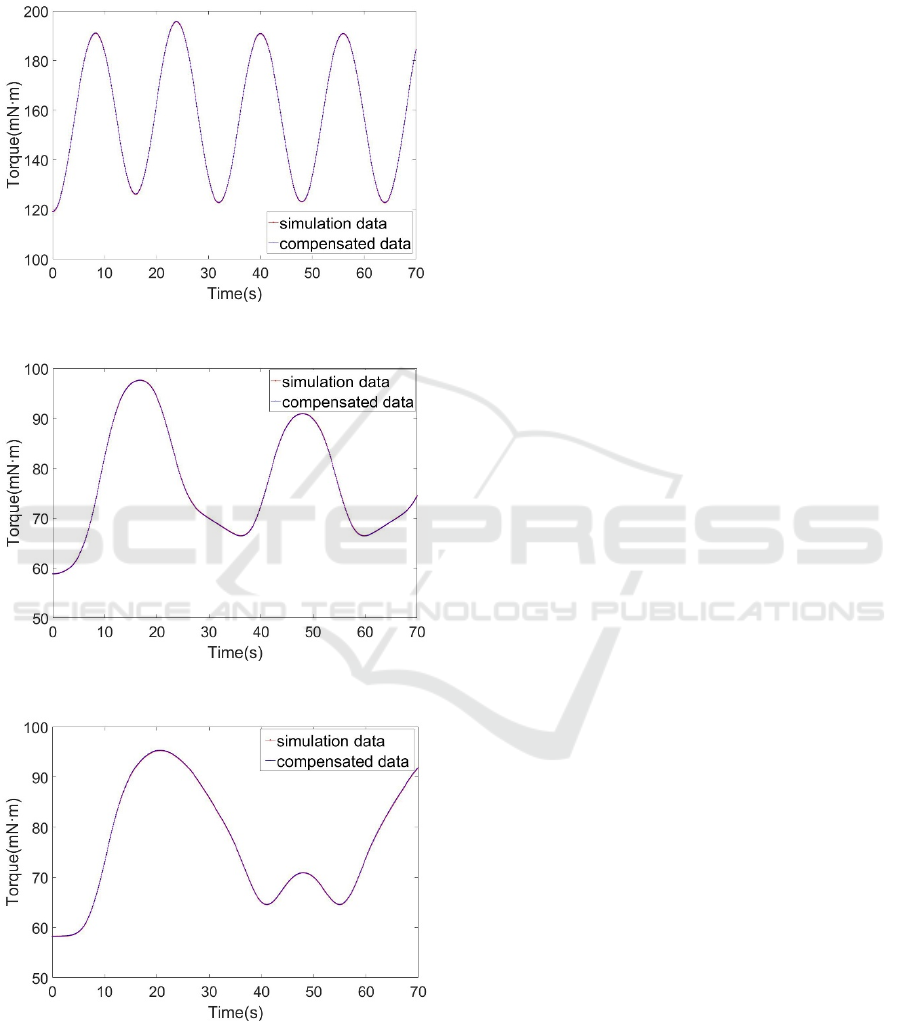
network in MATLAB. After adding the error to
equation (26), we can compare the simulation data
collected by ADAMS and the compensated data
calculated by MATLAB:
Figure 11: Simulation and compensated torque of joint 1.
Figure 12: Simulation and compensated torque of joint 2.
Figure 13: Simulation and compensated torque of joint 3.
From figures showed above, we can see that the
curve of the simulation data and the curve of the
compensated data almost coincide, the standard
deviation of three pairs of curve reduces to
0.053mN m
, 0.0498mN m
and 0.0302mN m .
5 CONCLUSIONS
The research of the gravity compensation algorithm
and its error compensation method of the haptic
device had been conducted. When we analysed the
system, we simplified the serial part as a whole and
added its mass to the moving platform which was part
of the parallel mechanism. Then we carried the
dynamic modelling with the principle of virtual work
and thereby fulfilling the goal of gravity
compensation. After that we compared the curve of
the simulation data and the curve of the compensated
data and found the errors between them. In order to
eliminate the errors, we designed a set of BP neural
network. Under the help of neural network, the errors
had been reduced greatly and this also proves the
effectiveness of the BP neural network on the error
elimination of gravity compensation.
REFERENCES
Codourey, A. 1998. Dynamic Modeling of Parallel Robots
for Computed-Torque Control Implementation. The
International Journal of Robotics Research, 17(12),
pp.1325-1336.
Okamura, A., Verner, L., Reiley, C. and Mahvash, M. 2010.
Haptics for Robot-Assisted Minimally Invasive
Surgery. Springer Tracts in Advanced Robotics,
pp.361-372.
Wang, J. and Gosselin, C. 1998. A new approach for the
dynamic analysis of parallel manipulators. Multibody
System Dynamics, 2(3), pp.317-334.
Zhang, L., Wang, S., Li, J. and Li, J. 2013. Design of a
Master Manipulator with Dynamical Simplification for
Master-Slave Robot. Applied Mechanics and Materials,
418, pp.3-9.
You, W., Kong, M., Du, Z. and Sun, L. 2008. High efficient
inverse dynamic calculation approach for a haptic
device with pantograph parallel platform. Multibody
System Dynamics, 21(3), pp.233-247.
Wu, B., Han, S., Xiao, J., Hu, X. and Fan, J. 2016. Error
compensation based on BP neural network for airborne
laser ranging. Optik - International Journal for Light
and Electron Optics, 127(8), pp.4083-4088.
Chu, J., Li, H. and Chen, X. 2013. Research on Improved
BP Learning Algorithm of BP Neural Network.
Advanced Materials Research, 765-767, pp.1644-1647.
Li, J., Cheng, J., Shi, J. and Huang, F. 2012. Brief
Introduction of Back Propagation (BP) Neural Network
Algorithm and Its Improvement. Advances in
Intelligent and Soft Computing, pp.553-558.
ICECTT 2018 - 3rd International Conference on Electromechanical Control Technology and Transportation
604

Ma, C., Zhao, L., Mei, X., Shi, H. and Yang, J. (2016).
Thermal error compensation of high-speed spindle
system based on a modified BP neural network. The
International Journal of Advanced Manufacturing
Technology, 89(9-12), pp.3071-3085.
A Gravity-Compensation Algorithm for the Haptic Device Based on the Principle of Virtual Work and BP Neural Network
605
