
Formalisms and Interfaces to Manipulate Music Information: The Case
of Music Petri Nets
Adriano Barat
`
e, Goffredo Haus and Luca A. Ludovico
Laboratorio di Informatica Musicale, Dipartimento di Informatica “Giovanni Degli Antoni”,
Universit
`
a degli Studi di Milano, Via Celoria 18, Milan, Italy
Keywords:
Music, Petri Nets, Formalization, Manipulation, Human-Computer Interfaces.
Abstract:
Music Petri nets are a mathematical formalism that has been already adopted in the context of music infor-
mation analysis and manipulation, concerning both symbolic scores and audio content. Among the main
advantages, it is worth mentioning their possibility to clearly describe music processes and transformations
inside a music composition, their easy-to-understand graphical representation, and the availability of formal
tools to analyze the nets thus obtained. But previous research has also highlighted some limits in the usabi-
lity of music Petri nets, due to an interface far from the ones composers and performers are used to, such as
digital score editors and digital audio workstations. In this paper, we propose a solution that combines the
descriptive power of such a mathematical formalism with the ease of use of editing tools to which musicians
are accustomed. The idea is to design human-computer interfaces that, standing between the musician and the
mathematical formalism, can hide the details of the underlying Petri nets.
1 INTRODUCTION
In the field of sound and music computing, the pro-
blem of finding suitable interfaces to represent and
manipulate music information is a matter of interest.
In 1985, Pennycook wrote an inspiring survey on
computer-music interfaces and their basic principles,
dealing specifically with three musical tasks: ma-
nuscript preparation, music language interfaces for
composition, and real-time performance interaction
(Pennycook, 1985). In more recent times, reference
(Assayag et al., 1999) mentioned examples of inter-
faces for computer-assisted composition developed at
IRCAM, (Cook, 2001) described the principles to de-
sign computer music controllers, and (Paradiso and
Omodhrain, 2003) dealt with trends in electronic mu-
sic interfaces. Finally, it is worth mentioning the
works annually presented at the International Con-
ference on New Interfaces for Musical Expression
(NIME), an initiative dedicated to scientific research
on the development of new technologies and their role
in musical expression and artistic performance.
A successful example of computer-music inter-
face is the reacTable (Jord
`
a et al., 2007), an electronic
musical instrument with a tabletop tangible user inter-
face conceived in 2003 and developed by a research
team at the Pompeu Fabra University in Barcelona.
In its original configuration, the interface is basically
a round translucent table, used in a darkened room as
a backlit display.
1
By placing blocks called tangibles
on the table, and interfacing with the visual display
via the tangibles or fingertips, a virtual modular synt-
hesizer is operated, thus creating music or sound ef-
fects. The reacTable is a musical instrument that can
be profitably used for extemporary composition and
performance. Similarly to our proposal detailed be-
low, tangibles can be associated with the concepts of
music object and musical operator that we will intro-
duce, but such an instrument has not been conceived
to describe music processes in a formal way.
MAX/Msp (Didkovsky and Hajdu, 2008) and Pure
Data (Puckette et al., 1996) are dataflow program-
ming languages where functions or objects are linked
in a graphical environment which models control and
audio flows. These software tools can also support
formal approaches to composition and manipulation
of music information, an aspect that brings them clo-
ser to our proposal. Since MAX/Msp and Pure Data
are commonly in use among musicians, this kind of
approach seems to be suitable also for people without
a specific training in sound and music computing.
Now, a key question is: why should we employ a
1
More recently, also software versions have been released.
Baratè, A., Haus, G. and Ludovico, L.
Formalisms and Interfaces to Manipulate Music Information: The Case of Music Petri Nets.
DOI: 10.5220/0007228500810090
In Proceedings of the 2nd International Conference on Computer-Human Interaction Research and Applications (CHIRA 2018), pages 81-90
ISBN: 978-989-758-328-5
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
81

formal tool to describe music objects and their trans-
formational processes, which implies a number of
theoretical and practical problems to solve, when non-
formal solutions to create and manipulate music and
sound are available and commonly in use?
The answer is that formal tools present a number
of advantages with respect to non-formal representa-
tion formats. First, for the representation, transfor-
mation, and establishment of relationships involving
music information, it is possible to rely on the theory
behind, also benefiting from previous research. Mo-
reover, a formal representation typically allows the
investigation of mathematical as well as topological
properties; an example is the automatic recognition of
identical structures via an isomorphism. Finally, the
adoption of a formalism encourages the unveiling of
hidden structures and implicit processes, thus foste-
ring a deeper understanding of the creative/analytical
phenomenon.
The paper is structured as follows: Section 2 will
make research questions explicit, Section 3 will pro-
vide an overview of the formalism known as Petri
nets, Section 4 will introduce a specialization called
music Petri nets, Section 5 will discuss some propo-
sals of interfaces which can answer the mentioned re-
search questions, and Section 6 will draw the conclu-
sions.
2 RESEARCH QUESTIONS
Petri nets (PNs) are a formal tool suitable to study and
describe systems that are concurrent, asynchronous,
distributed, parallel, and non-deterministic. Also mu-
sical compositions can be seen as the result of trans-
formational processes on music objects that share
many of the mentioned features. For example, parts
and voices in a composition can be interpreted as pa-
rallel, concurrent and distributed sequences of music
objects, which can be in turn decomposed into sim-
pler information entities.
In this context, we define music object any mea-
ningful aggregation of symbols, at different degrees
of abstraction. Given this very broad definition, ex-
amples of music objects may be sections, periods,
phrases, motifs, chord sequences, rhythmic patterns,
etc. Within a composition, music objects can be reu-
sed, as in the case of verse-chorus structures for po-
pular music or subject-answer-countersubject in con-
trapuntal compositional techniques. Besides, music
objects can be transformed through ad hoc music ope-
rators, such as transpositions, inversions, pitch substi-
tutions, etc. Since music is intrinsically hierarchical
(Lerdahl and Jackendoff, 1983), the process of de-
composition of music objects into simpler ones can
occur recursively, until the most atomic level (e.g., the
one of music symbols) has been reached.
Recent research in the field of music theory, music
cognition, and computational musicology has brought
to the formulation of theories where music processes
are made explicit, so as to unveil the structure of indi-
vidual compositions (Lerdahl and Jackendoff, 1985).
The research questions of the present work do not
focus on the possibilities offered by Petri nets to mu-
sic composition, analysis, and a posteriori manipula-
tion, since these aspects have been already investiga-
ted in literature (see Section 4.2 for further details).
Rather, our goal is to bridge the gap between a Petri
net-based representation of music content, which is
a formal tool comprehensible to mathematicians and
computer scientists, and a performance-oriented tool,
namely an interface that allows easy interaction with
music content suitable for composers and musicians.
In our intention, this initiative does not explicitly
address musicians, nor is aimed at providing only
domain experts with a new music-content manipula-
tion tool. Needless to say, musicians are a privileged
category of users both to validate the theoretical ap-
proach and to test the computer-based tools that im-
plement it, but our goal is to propose a new paradigm
to manipulate music content addressing also untrai-
ned people.
The main research questions for this work are:
a) Is it possible to hide the details of the Petri net des-
cription of a music piece, so that it can be easily ma-
naged even by non-experts while formal aspects are
being preserved? b) Is the proposed approach suitable
to define musical objects and support the main trans-
formational processes occurring on them, even in a
real time context? c) Is it possible to create a software
environment implementing the mentioned theoretical
framework?
Before answering the aforementioned research
questions, it is worth introducing some basic noti-
ons on Petri nets (PNs) and music Petri nets (MPNs),
which constitute a specialization of PNs in the music
field.
3 AN OVERVIEW OF PETRI
NETS
A formal description of the general net theory by
Carl Adam Petri would fall beyond the scope of the
present paper. For details about this subject, please
refer to works such as (Petri, 1980), (Peterson, 1981)
and (Murata, 1989). For the sake of clarity, we will
only summarize the key elements to let the reader un-
CHIRA 2018 - 2nd International Conference on Computer-Human Interaction Research and Applications
82

Figure 1: An example of Petri net, showing places (cir-
cles), transitions (rectangles), arcs (oriented lines) and their
weight (numbers above oriented lines). Numbers inside pla-
ces represent the current and the maximum number of to-
kens allowed, respectively. The former number provides
place marking.
derstand the theoretical approach proposed in the fol-
lowing.
A PN is an abstract and formal model to represent
the dynamic behavior of a system presenting asyn-
chronous and concurrent activities. PNs are made of
a combination of basic objects falling in one of these
categories: places, transitions, and arcs. Usually re-
presented in a graphical forms, the instances of such
categories are drawn as circles, rectangles, and orien-
ted lines respectively. Places and transitions are also
referred to as nodes. Arcs can have a number associ-
ated, called the arc weight. The graphical appearance
of a simple PN is shown in Figure 1.
PNs are not static models, rather they present an
evolution from a state to another. The current state is
indicated by place marking, namely by the number of
tokens in each place. The dynamic evolution of a PN
is determined by the following firing rules:
• A transition is enabled when all the incoming pla-
ces of that transition present a number of tokens
greater or equal to the weights of the correspon-
ding incoming arcs, and, after the fire of the tran-
sition, the marking of all the output places will be
less than or equal to their capacities;
• When a transition is enabled, its firing subtracts
from the incoming places a number of tokens
equal to the weights of the incoming arcs, and
adds to each outgoing place a number of tokens
equal to the weights of the corresponding out-
going arc.
An example of transition firing, showing markings
before and after, is provided in Figure 2.
When their application to the music field was first
proposed, the following properties were considered:
PNs are associated with a graphical form of notation
that requires few symbols; they support hierarchical
descriptions and the definition of macro-structures;
they are able to describe music-objects processing,
supporting timed representations and deterministic as
well as non-deterministic models (Haus and Sametti,
1991).
4 MUSIC PETRI NETS
Music Petri nets (MPNs) are a specialized extension
of PNs that supports the association of music objects
to places. A music object (MO) may be anything that
can have a musical meaning and can be thought as
an entity, either simple or complex, either abstract or
detailed. As we will explain below, MOs can be com-
bined, reused as they are, or transformed into new in-
stances.
For the sake of clarity, it is important to underline
the possibility to associate different kinds of music-
related content with places. In detail:
• In the case of symbolic content, the MO contains
score excerpts encoded in terms of Common Wes-
tern Notation (e.g., notes, rests, etc.) or other no-
tational systems. The main advantage is the pos-
sibility to manipulate objects at any degree of ab-
straction and granularity. For example, it is pos-
sible to implement algorithms such as “transpose
all notes of the first measure one octave below”,
Figure 2: The upper image shows a net where transition T1
is enabled, i.e. it is ready to fire; the lower image illustrates
the new net marking after firing. Please note that tokens
have not been transferred, rather consumed in input places
and created in output places in accordance with arc weights.
Formalisms and Interfaces to Manipulate Music Information: The Case of Music Petri Nets
83

or “double the duration of all C-pitched notes”.
On the other side, the corresponding audio is not
directly encoded within MOs; rather, playback re-
quires the interpretation of symbolic sequences to
be sent to a sound module;
• In the case of performance content, the MO em-
beds information encoded through a computer-
driven performance language, such as MIDI or
Csound. This kind of approach stands in the
middle of symbolic and audio content;
• In the case of audio content, the MO contains
waveforms instead of symbolic information. The
possibilities of content manipulations are far more
limited than in the first case (e.g., alteration of
the original sequence of audio fragments, volume
changes, equalization, pitch shifting, time stret-
ching, etc.); on the other side, for net playback,
only a suitable media player is required.
In the following, these cases will be managed se-
parately, and the proposed interface will remark dif-
ferences through ad hoc graphical features.
4.1 Formalization
Concerning places, in MPNs the following cases can
occur:
• A place can have no music fragment associated
and no music fragment in input. In this way, it has
only a structural function (e.g., a counter, a selec-
tor, a semaphore, etc.) in a given net topology, in
accordance with the definition of places in ordi-
nary PNs, where markings represent the state of
the system;
• A place can host a music fragment that will be
transferred to output places after the firing of the
corresponding transitions. In this case, the music
fragment will be delivered to output places after
the manipulation operated by transitions;
• A place can receive a music fragment from either
a single or multiple input transitions. If multiple
fragments arrive simultaneously and/or a MO is
already present, fragments are mixed to form a
more complex MO, potentially available for out-
going transitions.
Moreover, in MPNs a place can be either enabled
to play music objects or not. When an enabled place
containing a MO receives tokens, the fragment (either
already present or transferred from other places) is
played; when a non-enabled place hosts or receives
MOs, its only function is to mix inputs, store music
fragments and send them in output when transitions
fire.
Concerning transitions, in MPNs they can host
music algorithms (defined as abstract transformati-
ons). This kind of transitions is used to process MOs
in input, modify them accordingly, and transfer MOs
thus obtained in output.
For example, one can create a simple net with a
place with an associated MO containing a single note
(say, a C pitch) and the Play flag set to false, an output
transition with an associated algorithm that creates a
major scale in the key of the input note, and an output
place that plays the objects thus modified (in this case,
the C major scale). Then, the same net topology can
be reused by changing the MO associated with the
input place: e.g., if the original note is set to D, the
D major scale is obtained; as another example, if a
sequence of pitches is used as the input instead of a
single note, the final result is a progression.
For a more detailed formal description of MPNs,
please refer to (Barat
`
e and Haus, 2013).
4.2 Related Works on MPNs
The relationship between PNs and music has been in-
vestigated in a number of scientific works. This re-
search field has been explored since late ’80s mainly
at the Laboratory of Music Informatics (LIM – Labo-
ratorio di Informatica Musicale) of the University of
Milan.
Early works discussing the description and perfor-
mance of musical processes by means of Petri nets
are (Camurri et al., 1986) and (Haus and Rodriguez,
1988).
Reference (Haus and Sametti, 1991) introduces
ScoreSynth, an experimental software tool for score
synthesis through MPNs (see Section 4.3).
A discussion about the effectiveness of MPNs
in the formalizations of extended music pieces can
be found in (Haus and Rodriguez, 1993), focu-
sing on Ravel’s “Bolero”, and in (De Matteis and
Haus, 1996), dealing with Stravinsky’s “The Rite of
Spring”.
The possibility to rely on MPNs in order to re-
present the structure of a piece within a multi-layer
environment has been explored in (Barat
`
e, 2008) and
(Barat
`
e and Haus, 2013). The results of this investiga-
tion brought MPNs to become one of the formalisms
natively supported in the IEEE 1599 format (Baggi
and Haus, 2009) to provide structural descriptions for
music pieces.
Moreover, research has highlighted the applicabi-
lity of MPNs to music analysis (Barat
`
e et al., 2006)
and composition (Barat
`
e et al., 2007), even in real
time environments (Barat
`
e et al., 2014). A very re-
cent effort in this sense was the application of MPNs
CHIRA 2018 - 2nd International Conference on Computer-Human Interaction Research and Applications
84

to the formalization of Schoenberg’s fundamentals of
musical composition (Barat
`
e et al., 2018).
4.3 Available Software Tools
Currently, a number of software tools for the design
and execution of generic PNs is available. PIPE (Plat-
form Independent Petri net Editor)
2
is an open-source,
platform-independent tool for creating and analysing
Petri nets, including Generalised Stochastic Petri nets
(Dingle et al., 2009). The Petri Net Toolbox
3
is a soft-
ware tool for the simulation, analysis, and design of
discrete-event systems based on Petri Net models em-
bedded in the MATLAB environment. WoPeD (Work-
flow Petri Net Designer)
4
is an open-source software
which aims to provide an easy-to-use interface for
modelling, simulating and analyzing processes des-
cribed by workflow nets.
Concerning the musical extension of PNs, there is
only one available tool supporting MPNs: ScoreSynth
(Haus and Sametti, 1991). Its goal is to draw and exe-
cute MPNs supporting MOs encoded in IEEE 1599
format. This application, written in C], runs under
Microsoft Windows, even if recent tests have demon-
strated a good compatibility with Linux-based opera-
ting systems thanks to the Mono project.
Scoresynth has many features designed to draw
net models. Its multi-window GUI permits to ar-
range all Petri nets that concur to design a single
complex model. Customizable graphical elements in-
clude: place and transition sizes; place and transi-
tion names with customizable positions; place, tran-
sition, and arc background and foreground colors; arc
smoothness; pen widths; fonts; drawing grids. The
interface of ScoreSynth is shown in Figure 3.
In ScoreSynth, MPNs can be executed and debug-
ged in various ways:
• Complete execution – The standard execution
mode, where nets are processed until no transition
can fire, or the user stops the execution;
• Timed execution – Similar to the complete execu-
tion, but transition firings occurs every n seconds;
• Step-by-step execution – The user controls the
process by triggering single steps, such as transi-
tion firings, tokens transfer, performance of MOs.
To help debugging operations, an automatic text
report of net execution is provided, step by step. The
execution history is saved too, and the user can invoke
previous/next step buttons: this is also useful to test
2
http://pipe2.sourceforge.net/
3
https://www.mathworks.com/products/connections/
product detail/petri-net-toolbox.html
4
https://woped.dhbw-karlsruhe.de/
non-deterministic situations, stepping back and choo-
sing another execution branch of the net.
Since MOs are coded in IEEE 1599, a net exe-
cution creates a comprehensive IEEE 1599 document
that mixes all these objects, thus creating a final result
where the logic part reflects the mixing process, and
the linked media maintain their synchronization.
Together with printing and export graphics facili-
ties, an interesting feature consists in the file format
used to save models: PNML (Petri Net Markup Lan-
guage), which is an XML-based standard interchange
format used to represent PNs.
Currently, a Web-based multi-platform version of
ScoreSynth is under development at the Laboratory of
Music Informatics of the University of Milan.
The features of the original ScoreSynth have been
analyzed in order to support them in the proposed in-
terface, even if the purpose of this work is to hide PN-
implementation details.
5 A COMPUTER INTERFACE
FOR MUSIC PETRI NETS
In this section we will describe a proposal of soft-
ware tool, conceived as a browser application, which
aims to bridge the gap between traditional interfaces
for music manipulation and MPNs.
The first phase is the realization of a diagram
where MOs can be placed, modified through suita-
ble operators, and connected together as a graph. In
the following, please refer to Figure 4 for interface-
related aspects.
This phase can be decomposed into steps. First,
MOs are loaded into the Object Gallery, organized
by type, marked through a customizable name (e.g.,
“Fragment A”, “Main theme”, “Chorus”, etc.) and as-
sociated with a color. After the import step, using
drag-and-drop operations, MOs can be placed over
the canvas and connected by cords that join outlets
and inlets.
Inside the canvas, MOs are represented as rectang-
les, identified by a name, an icon, and a conventional
color that specifies the MO type. Depending on the
latter aspect, the rectangle adopts different graphical
representations for content: music notation in the case
of symbolic content, piano roll for computer-driven
performances, and waveforms for audio (see Figure
5). Each rectangle embeds basic media controls to
play its content; in case of non-audio blocks, an inter-
nal synthesizer is invoked.
For each block, multiple ingoing and outgoing
connections are supported. Cords may belong to two
Formalisms and Interfaces to Manipulate Music Information: The Case of Music Petri Nets
85

Figure 3: The interface of ScoreSynth for Microsoft Windows.
Figure 4: Screenshot of the proposed web-based interface.
CHIRA 2018 - 2nd International Conference on Computer-Human Interaction Research and Applications
86
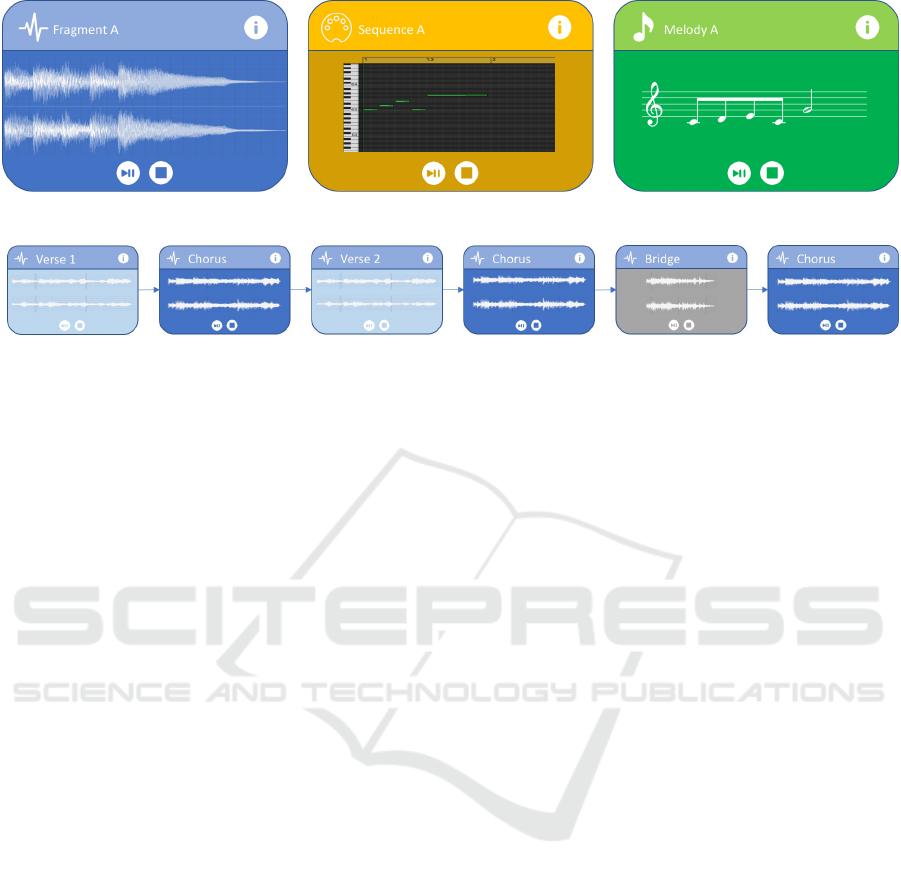
Figure 5: Graphical representations of audio, computer-driven performance, and symbolic MOs respectively.
Figure 6: Diagram of a “contrasting verse-chorus with bridge” song form, reconstructed by joining audio fragments obtained
from a segmentation process.
different types: a) concurrent arcs, represented by so-
lid lines, meaning that all concurrent outgoing paths
are traveled simultaneously, and b) exclusive arcs, re-
presented by dashed lines, implying that a path exclu-
des the others. Priority depends on numeric values
over arcs, that create a sorted sequence of arcs to be
navigated.
If no operator is invoked, the final result will
be a graph of music excerpts without any modifica-
tion. A simple example that illustrates a typical song
structure, specifically a contrasting verse-chorus with
bridge, is shown in Figure 6. In this case, MOs cor-
respond to high-level descriptions of the composition.
Please note that such an abstract representation con-
siders Verse 1 and Verse 2 as identical, whereas audio
signals (as well as score excerpts) would be typically
different, at least concerning lyrics.
The proposed framework supports another impor-
tant feature of MPNs, namely the availability of musi-
cal operators that can be applied to MOs in order to al-
gorithmically transform them into new MOs. Musical
operators can manipulate information concerning me-
lodic, harmonic and rhythmic aspects. Examples in-
volving symbolic content are transposition by a given
interval, inversion, calculation of the retrograde, aug-
mentation and diminution, and so on. Processes can
be applied in a selective way (e.g., “Transpose only
G-pitched eighth notes one octave below”) and they
can carry parameters (e.g., “Transpose all notes in the
sequence x halftones up”, with x ∈ N). Audio content
can be modified through different operators, such as
pitch shifting, time stretching, fade-in and fade-out,
filters, and other effects.
In MPNs, musical operators are typically linked to
transitions: when the transition fires, the correspon-
ding musical operator is triggered, thus modifying
the MOs contained in input places and “passing” the
transformed MOs to output places. This process, for-
mally defined in MPN theory, is hard to understand
for non experts. In the proposed interface, musical
operators are associated with blocks, and they can be
stacked one on top of the other. Rectangles, originally
conceived to carry only music content, now contain
tab views that allow to track step-by-step the transfor-
mations achieved by single musical operators. Figure
7 shows a clarifying example about cascading trans-
formations of audio content: a sine wave is first trans-
posed one octave below (pitch shifting by a factor 0.5)
and then faded out after a given number of samples.
The figure illustrates the graphical aspect of the three
panels contained in the same block.
After consolidating the structure of the graph, the
second phase, called macro expansion, can occur. The
goal is to turn such a diagram into a MPN. In com-
puter science, a macroinstruction (or simply macro)
is a rule or pattern that specifies how a certain input
sequence should be mapped to a replacement output
sequence according to a defined procedure. Macro
expansion stands for the mapping process that instan-
tiates a macro use into a specific sequence.
Under our working hypotheses, macro expansion
is trivial. Each block of the original graph can be ea-
sily substituted by a suitable subnet. When musical
operators have to be applied, the corresponding algo-
rithms are implemented within transitions. The cords
become arcs that join subnets together, possibly weig-
hted by probabilistic values in order to support exclu-
sive paths.
The third phase, called post-processing, works on
MPNs resulting from the previous phase and seeks for
known structures in order to improve their representa-
tion. For example, if in the original graph a MO cal-
Formalisms and Interfaces to Manipulate Music Information: The Case of Music Petri Nets
87

Figure 7: Panels of a block containing musical operators, showing step-by-step transformations that content undergoes and
allowing to set parameters.
led A is followed by A
∗
, obtained from A by applying
some musical operators, the macro expansion would
create a place loading and playing A, followed by a
transition that enables a new place loading A again,
followed by a transition that first applies the required
transformation on A (thus obtaining A
∗
) and then pas-
ses the modified music fragment to a new place that
performs it. Conversely, post-processing would pro-
vide a beautified MPN, more effective and compact
from a structural point of view: A would be loaded
into a sounding place only one time and played the
first time as is, than a transition would modify it and
transfer the result back to the same place, thus obtai-
ning the performance of A
∗
.
In conclusion, even if the macro expansion phase
produces semantically correct PNs by applying very
simple conversion algorithms, post-processing can
significantly improve PN structure, making some ad-
ditional music features emerge.
A complete example based on the nursery rhyme
called Fr
`
ere Jacques is shown in Figure 8. The tune
has been segmented into 4 fragments, called A, A
0
, B,
and C. Fragment A
0
can be obtained from A by dele-
ting the last note and transposing the remaining pit-
ches two grades up. The second voice is identical to
the first one, with an offset of 2 measures; this voice
is triggered by the second instance of A in the first
voice. Please note the use of both concurrent and ex-
clusive arcs, the latter with a priority value. Finally,
the MPN shown in Figure 8 is the result of the post-
processing phase, where the occurrence of two iden-
tical macro-expansions is recognized and encoded by
adding a backward arc from “Alg” to “Start”, and mo-
difying both the marking and the capacity of place
“StopMain” to 2 tokens.
6 CONCLUSIONS
In this work, we have outlined the functional and
graphical characteristics of a tool that lets users mani-
pulate music structures and content via a GUI, produ-
cing also a formal description in terms of music Petri
nets.
Recalling research question a (see Section 2),
from an early and limited experimentation performed
so far on a mock-up solution, the proposed appro-
ach seems to be effective also for people with no
specific training in Computer Science and Petri nets.
Answering research question b required to analyze
MPNs’ expressive power (e.g., the possibility to focus
on different degrees of aggregation/abstraction, orga-
nize structures thanks to the recursive use of subnets,
etc.), and consequently design a graph-oriented envi-
ronment where to place and connect blocks suppor-
ting most features of MPNs. Unfortunately, real-time
transformations of net topology and on-the-fly substi-
tutions of music content are still posing practical pro-
blems to solve. Another unsupported feature, at the
moment of writing, is non-determinism. These as-
pects will be further explored in our future research.
Concerning research question c, the theoretical fra-
mework is ready to be implemented, and a release in
form of a browser application is under development.
As it regards future work, after completing the
implementation, this solution requires to be extensi-
vely tested and validated by multiple categories of
users (e.g., composers, performers, musicologists,
non-experts, etc.). Besides, its functions can be exten-
ded, for instance by supporting a language to imple-
ment user-defined musical operators and improving
the post-processing phase.
REFERENCES
Assayag, G., Rueda, C., Laurson, M., Agon, C., and De-
lerue, O. (1999). Computer-assisted composition at
IRCAM: From PatchWork to OpenMusic. Computer
Music Journal, 23(3):59–72.
Baggi, D. L. and Haus, G. (2009). IEEE 1599: Music en-
coding and interaction. Ieee Computer, 42(3):84–87.
Barat
`
e, A. (2008). Music description and processing: An
approach based on Petri nets and XML. In Petri Net,
Theory and Applications. InTech.
CHIRA 2018 - 2nd International Conference on Computer-Human Interaction Research and Applications
88
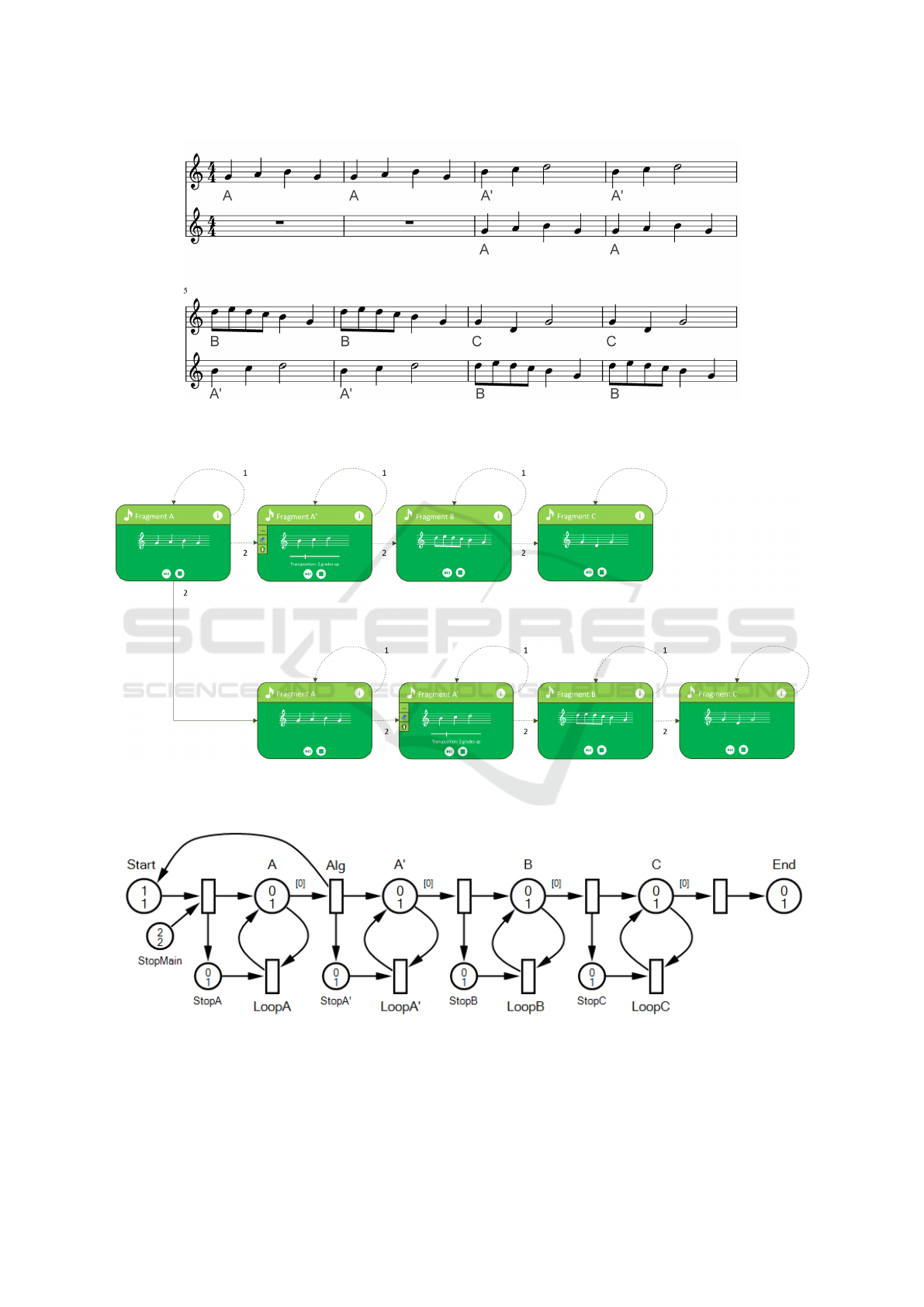
Figure 8: Score of Fr
`
ere Jacques (above), the corresponding graph (middle), and the music Petri net obtained after post-
processing (below).
Formalisms and Interfaces to Manipulate Music Information: The Case of Music Petri Nets
89

Barat
`
e, A., Haus, G., and Ludovico, L. A. (2006). Music
analysis and modeling through Petri nets. Computer
Music Modeling and Retrieval, pages 201–218.
Barat
`
e, A., Haus, G., and Ludovico, L. A. (2007). Petri
nets applicability to music analysis and composition.
In Proceedings of the International Computer Music
Conference’07 (ICMC 2007), pages 97–100.
Barat
`
e, A., Haus, G., and Ludovico, L. A. (2014). Real-
time music composition through P-timed Petri nets.
In Georgaki, A. and Kouroupetroglou, G., editors,
ICMC—SMC—2014 Proceedings, Athens 14-20 Sep-
tember 2014, pages 408–415, Athens.
Barat
`
e, A., Haus, G., Ludovico, L. A., and Mauro, D. A.
(2018). Formalizing Schoenbergs fundamentals of
musical composition through Petri nets. In Procee-
dings of the 15th International Sound and Music Com-
puting Conference (SMC 2018), Limassol, Cyprus,
pages 260–264.
Barat
`
e, A. and Haus, G. M. (2013). Structuring music in-
formation. In Baggi, D. and Haus, G., editors, Music
Navigation with Symbols and Layers: Toward Con-
tent Browsing with IEEE 1599 XML Encoding, pages
37–56. John Wiley and Sons, Hoboken.
Camurri, A., Haus, G., and Zaccaria, R. (1986). Describing
and performing musical processes by means of Petri
nets. Journal of New Music Research, 15(1):1–23.
Cook, P. (2001). Principles for designing computer music
controllers. In Proceedings of the 2001 conference
on New interfaces for musical expression, pages 1–4.
National University of Singapore.
De Matteis, A. and Haus, G. (1996). Formalization of
generative structures within Stravinsky’s The rite of
Spring. Journal of New Music Research, 25(1):47–76.
Didkovsky, N. and Hajdu, G. (2008). Maxscore: Music
notation in Max/MSP. In ICMC.
Dingle, N. J., Knottenbelt, W. J., and Suto, T. (2009).
Pipe2: a tool for the performance evaluation of gene-
ralised stochastic petri nets. ACM SIGMETRICS Per-
formance Evaluation Review, 36(4):34–39.
Haus, G. and Rodriguez, A. (1988). Music description and
processing by Petri nets. Advances in Petri Nets 1988,
pages 175–199.
Haus, G. and Rodriguez, A. (1993). Formal music repre-
sentation; a case study: the model of Ravel’s Bolero
by Petri nets. Music Processing. Computer Music and
Digital Audio Series, pages 165–232.
Haus, G. and Sametti, A. (1991). Scoresynth: a system for
the synthesis of music scores based on Petri nets and
a music algebra. Computer, 24(7):56–60.
Jord
`
a, S., Geiger, G., Alonso, M., and Kaltenbrunner, M.
(2007). The reactable: exploring the synergy between
live music performance and tabletop tangible interfa-
ces. In Proceedings of the 1st international confe-
rence on Tangible and embedded interaction, pages
139–146. ACM.
Lerdahl, F. and Jackendoff, R. (1983). An overview of hier-
archical structure in music. Music Perception: An In-
terdisciplinary Journal, 1(2):229–252.
Lerdahl, F. and Jackendoff, R. S. (1985). A generative the-
ory of tonal music. MIT press.
Murata, T. (1989). Petri nets: Properties, analysis and ap-
plications. Proceedings of the IEEE, 77(4):541–580.
Paradiso, J. A. and Omodhrain, S. (2003). Current trends
in electronic music interfaces. Journal of New Music
Research, 32(4):345–349.
Pennycook, B. W. (1985). Computer-music interfaces: a
survey. ACM Computing Surveys (CSUR), 17(2):267–
289.
Peterson, J. L. (1981). Petri net theory and the modeling of
systems. Prentice Hall PTR.
Petri, C. A. (1980). Introduction to general net theory. In
Net theory and applications, pages 1–19. Springer.
Puckette, M. et al. (1996). Pure Data: another integrated
computer music environment. Proceedings of the se-
cond intercollege computer music concerts, pages 37–
41.
CHIRA 2018 - 2nd International Conference on Computer-Human Interaction Research and Applications
90
