Application of Linear Programming on Example of Relationship

between Two Types of Activity and Optimized Dietary Supplement

Intake

Ana Špirelja Gruić

and Igor Gruić

V. Gymnasium, Klaićeva 1, 10000 Zagreb, Croatia

Faculty of Kinesiology, University of Zagreb, Horvaćanski zavoj 15, 10000 Zagreb, Croatia

Keywords: Mathematics, Linear Programming, Optimization, Nutrition, Health, Training, Kinanthropology.

Abstract: Kinesiology, as a science on movement, can use reductive and constructive logic and tools to inspect, analyse

and produce phenomena related to human, activity. Deterministic and stochastic nature of kinanthropological

phenomena are often analysed by complex statistical methods. Application of linear programming for

optimization in producing simple decision and recommendation regarding intake of exact proportion of

recovery dietary supplements complexes in two different activities (aerobic and anaerobic) revealed elegance

of the method, and revealed prospective practical implication in sport practice, rehabilitation process, and in

everyday life.

1 INTRODUCTION

Decision making is mostly rational act, based on good

estimates and facts, but in real life it often depends on

feelings, intuition, and happiness. It becomes harder

to decide when more different conditions have to be

fulfilled in order to reach the best possible (optimal)

decision. Mathematical modelling and programming

can be helpful, to different varying degree, depending

on the nature of the observed phenomenon and the

complexity of the problem (Špirelja, 2007).

Within general knowledge of multicriteria linear

optimizations (Ehrgott, 2005, Neralić, 2003, Steuer,

1986, Špirelja, 2007), analysis of relations and

differences between dietary/nutrition regimes (Aird

et al., 2018, Denham, 2017, Ferguson et al., 2004,

Henson, 1991, Rawson et al., 2018 ), and influences

of different training/exercise regimes (Pasiakos et al.,

2015, Patel et al., 2017), specific optimizations by

implementation of mathematical tools were feasible

and applicable (Asano et al., 2018, Briend et al., 2018,

Persson et al., 2018,)

The aim of this paper was, through a cross-section

of mathematical methods and two concrete example

of linear programming, to provide a practical tool for

optimizing simple and everyday needs for sport, but

also for everyday life, out of the relationship between

two types of activity and optimized input of dietary

supplement (DS).

2 METHODS

2.1 Linear Programming with Two

Variables

For those problems which have linear nature and

require only two variables (e.g. dietary supplements),

it is sufficient to know the graphical solution of linear

inequalities and the mathematical fact that the

optimum solution lies in one of the vertices of a

feasible set, defined by the constraints (cross section

of linear inequalities).

2.2 Linear Programming with More

Variables – A Simplex Method

Finding the vertex of the feasible set by the graphical

method in a more-than-two-dimensional space is

often demanding and time-consuming. A simpler

approach is to apply the Simplex Method, which is an

iterative method, i.e. step-by-step method of

improvements of the basic feasible solution, until the

final step results with optimal feasible solution (if it

Grui

c, A. and Grui

c, I.

Application of Linear Programming on Example of Relationship between Two Types of Activity and Optimized Dietary Supplement Intake.

DOI: 10.5220/0007234601970202

In Proceedings of the 6th International Congress on Sport Sciences Research and Technology Support (icSPORTS 2018), pages 197-202

ISBN: 978-989-758-325-4

197

exists). It mostly implies application of Gauss-Jordan

transformations of matrices which can be solved

manually and by different software tools.

2.3 Experimental Design

Dietary supplements (DS) for recovery after intensive

activity have the function of supplying body with

calories, proteins, amino acids (BCAA, Glutamine),

electrolytes (e.g. magnesium ions), vitamins (B1, B2,

B6) etc. The goal of the ‘optimization’ was to

calculate minimum intake of DS as possible within

the default features of the training and the limit on the

input.

Table 1: An example of a composition of three related DS

(mass in one portion of DS1:91g, DS2:75g, DS3:65g).

portion DS 1 DS 2 DS 3

calories 320 270 235

carbohydrates 60 53 28

proteins 20 13 27

B1 0.008 0.005 0.0033

B2 0.0085 0.004 0.0066

B6 0.008 0 0.0033

Mg 0.250 0.160 0.205

BCAA 4.5 0.98 5.98

Glutamine 6 1.56 0

In addition to regular activity and controlled diets,

for the purpose of this example, constraints for intake

of a part of the vitamin B complex are:

• B1 less than 7mg

• B2 less than 7mg

• B6 less than 7mg

2.3.1 Anaerobic Training

Consumption in the chosen anaerobic training in the

example assumes intake of:

• more than 280kcal

• more than 15g of protein

• more than 200mg of magnesium

• more than 2g of BCAA amino acids

• more than 3g amino acids Glutamine

2.3.2 Aerobic Training

Consumption in the chosen aerobic training in this

example assumes intake of:

• more than 320kcal

• more than 55g of carbohydrates

• more than 15g of protein

• more than 200mg of magnesium

• more than 2g of BCAA amino acids

• more than 3g amino acids Glutamine

3 OPTIMIZATION OF INTAKE

OF TWO DIETARY

SUPPLEMENTS

3.1 Relationship between Anaerobic

Activity and Optimized Intake of

Two Dietary Supplements

For variables X1 - the mass of portion intake of the

DS1, X2 - the mass of portion intake of the DS2, with

regard to default constraints and parameters, and Z -

objective (goal) function linear optimization problem

for anaerobic training was set:

MINIMIZE: Z = 91 X1 + 75 X2 (1)

320 X1 + 270 X2 ≥ 280

20 X1 + 13 X2 ≥ 15

0.25 X1 + 0.16 X2 ≥ 0.2

4.5 X1 + 0.98 X2 ≥ 2

6 X1 + 1.56 X2 ≥ 3

0.008 X1 + 0.005 X2 ≤ 0.007

0.0085 X1 + 0.004 X2 ≤ 0.007

0.008 X1 ≤ 0.007

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

X1, X2 ≥ 0 (10)

The feasible set is pentagon (Figure 1), and the

candidates for the optimal solution are in vertices of

that pentagon. The optimal solution is in the vertex in

which the objective function reaches the minimum

value.

The solution is in vertex F (0.56, 0.37), which

would mean that the optimal combination of two

preparations is: DS1 51.36 g and DS2 28.58 g.

K-BioS 2018 - Special Session on Kinesiology in Sport and Medicine: from Biomechanics to Sociodynamics

198

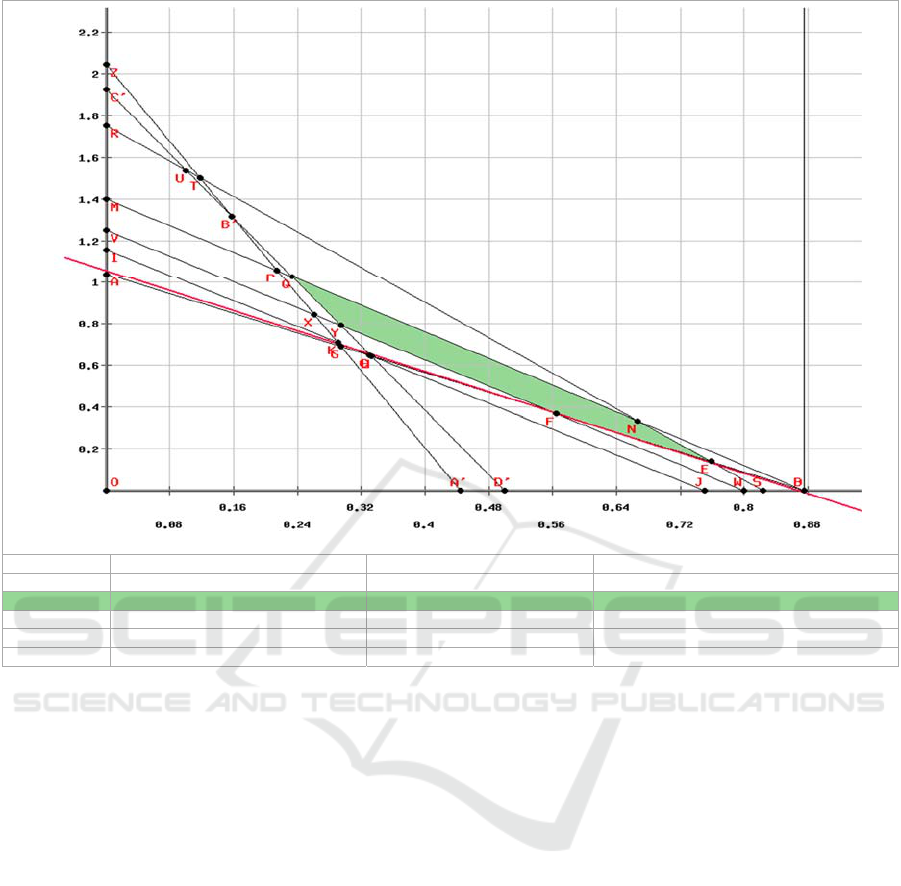
Point X coordinate

(

)

Y coordinate

(

)

Value of the ob

ective function

(

)

E 0.75862068965517 0.13793103448276 79.379310344828

F 0.56441717791411 0.3680981595092 78.969325153374

N 0.66666666666667 0.33333333333333 85.666666666667

0.23287671232877 1.027397260274 98.246575342466

Y 0.29473684210526 0.78947368421053 86.031578947368

Figure 1: Anaerobic training parameters.

3.2 Relationship between Aerobic

Activity and Optimized Intake of

Two Dietary Supplements

For variables X1 - the mass of portion intake of the

DS1, X2 - the mass of portion intake of the DS2, with

regard to default constraints and parameters, and Z -

objective (goal) function linear optimization problem

for aerobic training was set:

MINIMIZE: Z = 91 X1 + 75 X2

(1)

320 X1 + 270 X2 ≥ 320

(2)

20 X1 + 13 X2 ≥ 15

(3)

0.25 X1 + 0.16 X2 ≥ 0.2

(4)

4.5 X1 + 0.98 X2 ≥ 2

(5)

6 X1 + 1.56 X2 ≥ 3

(6)

60 X1 + 53 X2 ≥ 55

(7)

0.008 X1 + 0.005 X2 ≤ 0.007

(8)

0.0085 X1 + 0.004 X2 ≤ 0.007

(9)

0.008 X1 ≤ 0.007

(10)

X1, X2 ≥ 0

(11)

The feasible set is triangle (Figure 2), and the

candidates for the optimal solution are vertices of that

triangle. The optimal solution is the vertex in which

the function of the target reaches the minimum value.

The solution is at point H (0.28, 0.86) which would

mean that the optimal combination of two

preparations: DS1 25.27 g, and DS2 64.24 g.

4 OPTIMIZATION OF INTAKE

OF MORE DIETARY

SUPPLEMENTS

In next example three different dietary supplements

were included. Graphical method, presented in

previous examples, would here require plotting linear

inequalities in 3-D and defining feasible region.

Simplex method will then be more appropriate.

Application of Linear Programming on Example of Relationship between Two Types of Activity and Optimized Dietary Supplement Intake

199

Point X coordinate (X1) Y coordinate (X2) Value of the objective function (Z)

C 0.51785714285714 0.57142857142857 89.982142857143

H 0.27730192719486 0.85653104925054 89.474304068522

S 0.23287671232877 1.027397260274 98.246575342466

Figure 2: Aerobic training parameters.

4.1 Relationship between Anaerobic

Activity and Optimized Intake of

Three Dietary Supplements

For variables X1 - the mass of portion intake of the

DS1, X2 - the mass of portion intake of the DS2, X3

- the mass of portion intake of the DS3, with regard

to default constraints and parameters, and Z -

objective (goal) function linear optimization problem

for anaerobic training was set:

MINIMIZE: Z = 91 X1 + 75 X2 + 65 X3

(1)

320 X1 + 270 X2 + 235 X3 ≥ 280

(2)

20 X1 + 13 X2 + 27 X3 ≥ 15

(3)

0,25 X1 + 0,16 X2 + 0,205 X3 ≥ 0,2

(4)

4,5 X1 + 0,98 X2 + 5,98 X3 ≥ 2

(5)

6 X1 + 1,56 X2 + 0 X3 ≥ 3

(6)

0,008 X1 + 0,005 X2 + 0,0033 X3 ≤ 0,007

(7)

0,0085 X1 + 0,004 X2 + 0,0066 X3 ≤ 0,007

(8)

0,008 X1 + 0 X2 + 0,0033 X3 ≤ 0,007

(9)

X1, X2, X3 ≥ 0

(10)

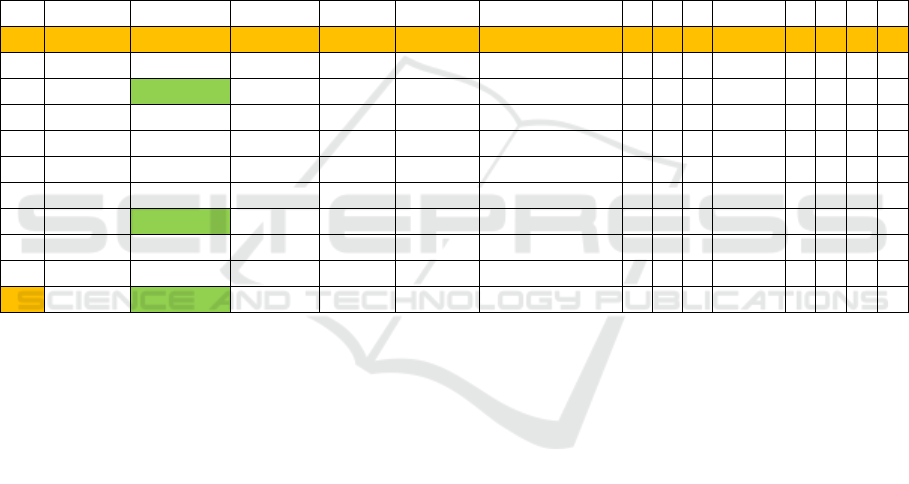
The optimal solution (in table 2) is (0.3864, 0.4368,

0.1634) which would mean that the optimal

combination of three preparations is: DS1 35.16 g,

DS2 32.76 g and DS3 10.62 g.

Table 2: Final solution shown in transformed matrix after six iterations (by using simplex method).

-91,0000 -75,0000 -65,0000 0 0 0 0 0 0 0 0 0

Base Cb P0 P1 P2 P3 P4 P5 P6 P7 P8 P9 P10 P11 P12

P2 -75,0000 0,4368 0 1 0 -0,0128 0 14,7160 0 0,0715 0 0 0 0

P7 0,0000 1,1444 0 0 0 0,0380 0 -72,7481 1 0,2537 0 0 0 0

P3 -65,0000 0,1634 0 0 1 0,0059 0 -11,6977 0 0,1701 0 0 0 0

P1 -91,0000 0,3864 1 0 0 0,0033 0 -3,8262 0 -0,1853 0 0 0 0

P5 0,0000 2,8198 0 0 0 0,0605 1 -201,0520 0 1,8176 0 0 0 0

P9 0,0000 0,0012 0 0 0 178533408,4789 0 -0,0044 0 0,0006 1 0 0 0

P10 0,0000 0,0009 0 0 0 -162846765,6084 0 0,0509 0 0,0002 0 1 0 0

P11 0,0000 0,0034 0 0 0 -46333521,1973 0 0,0692 0 0,0009 0 0 1 0

P12 0,0000 0,0000 0 0 0 0,0000 0 0,0000 0 0,0000 0 0 0 1

-78,5482 0 0 0 0,2724 0 4,8281 0 0,4383 0 0 0 0

K-BioS 2018 - Special Session on Kinesiology in Sport and Medicine: from Biomechanics to Sociodynamics

200

4.2 Relationship between Aerobic

Activity and Optimized Intake of

Three Dietary Supplement

For variables X1 - the mass of portion intake of the

DS1, X2 - the mass of portion intake of the DS2, X3

- the mass of portion intake of the DS3, with regard

to default constraints and parameters, and Z -

objective (goal) function linear optimization

problem for aerobic training was set:

MINIMIZE: Z = 91 X1 + 75 X2 + 65 X3

(1)

320 X1 + 270 X2 + 235 X3 ≥ 320

(2)

20 X1 + 13 X2 + 27 X3 ≥ 15

(3)

0,25 X1 + 0,16 X2 + 0,205 X3 ≥ 0,2

(4)

4,5 X1 + 0,98 X2 + 5,98 X3 ≥ 2

(5)

6 X1 + 1,56 X2 + 0 X3 ≥ 3

(6)

0,008 X1 + 0,005 X2 + 0,0033 X3 ≤ 0,007

(7)

0,0085 X1 + 0,004 X2 + 0,0066 X3 ≤ 0,007

(8)

0,008 X1 + 0 X2 + 0,0033 X3 ≤ 0,007

(9)

60 X1 + 53 X2 + 28 X3 ≥ 55

(10)

X1, X2, X3 ≥ 0

(11)

The optimal solution (in table 3) is (0.2773, 0.8565,

0) which would mean that the optimal combination

of three preparations is: DS1 25.23 g, DS2 64.24 g

and DS3 0 g.

Table 3: Final solution shown in transformed matrix after eleven iterations (by using simplex method).

-91,0000 -75,0000 -65,0000 0 0 0 0 0 0 0 0 0

Base Cb P0 P1 P2 P3 P4 P5 P6 P7 P8 P9 P10 P11 P12

P6 0,0000 0,0064 0 0 -0,0855 -0,0005 0 1 0 -0,0145 0 0 0 0

P2 -75,0000 0,8565 0 1 1,2580 -0,0054 0 0 0 0,2855 0 0 0 0

P7 0,0000 0,0873 0 0 -6,2190 0,0010 0 0 1 -0,8042 0 0 0 0

P10 0,0000 0,0012 0 0 0,0043 95824411,1349 0 0 0 0,0009 0 1 0 0

P12 0,0000 7,0343 0 0 19,0503 -0,2002 0 0 0 0,6781 0 0 0 1

P9 0,0000 0,0005 0 0 -0,0004 156316916,4882 0 0 0 0,0005 1 0 0 0

P1 -91,0000 0,2773 1 0 -0,3271 0,0014 0 0 0 -0,2409 0 0 0 0

P11 0,0000 0,0048 0 0 0,0059 -111349036,4026 0 0 0 0,0019 0 0 1 0

P5 0,0000 1,6809 0 0 -17,1874 -0,0418 1 0 0 -1,1064 0 0 0 0

-89,4743 0 0 0,4127 0,2748 0 0 0 0,5086 0 0 0 0

5 CONCLUSIONS

The problem of choosing a suitable method in sports

research, in this case the introduction of recovery

preparations and dietary supplements, is a key issue

because of the often stochastic nature of the observed

variables.

In the latest trends in research in sports and

kinesiology, there is the concept of 'vicarianza'

(Sibilio, 2017), through which different variables of

input are set into the relationship with the rules of the

observed activity (e.g. rules of handball, tactics, or

verified protocol of therapeutic procedure after

operative procedure, etc.), then through decision-

making mechanisms, all the way to last and finite,

mostly measurable effects of the activity described by

input variables. In this context, linear multicriteria

optimizations tool was useful for introducing DS3 as

appropriate for recovery after anaerobic training, but

not necessary for recovery after aerobic training.

ACKNOWLEDGEMENTS

This paper is announcement of future cooperation

between laboratories of Institute of Kinesiology,

Faculty of Kinesiology University of Zagreb, and

high school of natural and mathematical sciences V.

Gymnasium Zagreb within project “School for life”

supported by Ministry of Science and Education,

Republic of Croatia.

REFERENCES

Aird, T. P., Davies, R. W., Carson, B. P. (2018) Effects of

fasted vs fed

‐

state exercise on performance and post

‐

exercise metabolism: A systematic review and meta

‐

analysis. Scandinavian Journal of Medicine and

Science in Sports. Vol: 28(5):1476-1493, DOI:

https://doi.org/10.1111/sms.13054

Asano, K., Yang, H., Lee, Y., Yoon, J. (2018). Designing

optimized food intake patterns for Korean adults using

Application of Linear Programming on Example of Relationship between Two Types of Activity and Optimized Dietary Supplement Intake

201

linear programming (I): analysis of data from the

2010~2014 Korea National Health and Nutrition

Examination Survey, Journal of Nutrition and Health,

Vol 51(1):73-86. DOI: https://doi.org/10.4163/jnh.

2018.51.1.73

Briend, A., Darmon, N., Ferguson, E., Erhardt, J.G. (2003)

Linear Programming: A Mathematical Tool for

Analyzing and Optimizing Children's Diets During the

Complementary Feeding Period, Journal of Pediatric

Gastroenterology and Nutrition, Vol: 36(1):12-22

Denham, B.E. (2017). Athlete Information Sources About

Dietary Supplements: A Review of Extant Research,

International Journal of Sport Nutrition and Exercise

Metabolism, Vol: 27(4):325-334, DOI:

https://doi.org/10.1123/ijsnem.2017-0050

Ehrgott, M. (2005), Multicriteria optimization, Springer,

Heidelberg, 2005.

Ferguson E.L., Darmon N., Briend A., Premachandra I.M.

(2004). Food-Based Dietary Guidelines Can Be

Developed and Tested Using Linear Programming

Analysis. The Journal of Nutrition, Vol 134(4):951–

957, DOI: https://doi.org/10.1093/jn/134.4.951

Henson, S. (1991). Linear programming analysis of

constraints upon human diets. Journal of Agricultural

Economics, Vol: 42(3):380-393, DOI:

https://doi.org/10.1111/j.1477-9552.1991.tb00362.x

Neralić, L. (2003). Introduction to linear programming

(Uvod u matematičko programiranje) 1, Element,

Zagreb, 2003.

Pasiakos, S.M., McLellan, T.M. & Lieberman, H.R. Sports

Med (2015) The Effects of Protein Supplements on

Muscle Mass, Strength, and Aerobic and Anaerobic

Power in Healthy Adults: A Systematic Review. Sports

Medicine, Vol 45(1):111–131, DOI:

https://doi.org/10.1007/s40279-014-0242-2

Patel, H., Alkhawam, H., Madanieh, R., Shah, N., Kosmas,

C.E., and Vittorio, T.J. (2017) Aerobic vs anaerobic

exercise training effects on the cardiovascular system.

World Journal of Cardiology. Vol: 9(2):134–138. DOI:

https://doi.org/10.4330/wjc.v9.i2.134

Persson, M., Fagt, S., Pires, S.M., Poulsen, M., Vieux, F.,

Nauta M.J. (2018). Use of Mathematical Optimization

Models to Derive Healthy and Safe Fish Intake. The

Journal of Nutrition, Vol: 148(2):275–284, DOI:

https://doi.org/10.1093/jn/nxx010

Rawson, E.S., Miles, M.P., Larson-Meyer, D.E. (2018).

Dietary Supplements for Health, Adaptation, and

Recovery in Athletes. International Journal of Sport

Nutrition and Exercise Metabolism Vol: 28(2):188-

199, DOI: https://doi.org/10.1123/ijsnem.2017-0340

Sibilio, M. (2017). Vicarianza e didattica – corpo,

congnizione, insegnamento. ELS La Scuola, Editrice

Morcelliana, Brescia, ISBN 978-88-350-4617-2

Steuer R.E., (1986). Multiple Criteria Optimization:

Theory, Computation and Applications. John Wiley &

Sons, Inc, 1986.

Špirelja, A. (2007) Nonlinear multicriteria optimization

(Nelinearna višekriterijska optimizacija). Zagreb:

Faculty of Science University of Zagreb

PHPSimplex - online simplex method solver

http://www.zweigmedia.com/RealWorld/simplex.html

http://www.mathstools.com/section/main/simplex_online_

calculator#.UdHztJw1nzc.

K-BioS 2018 - Special Session on Kinesiology in Sport and Medicine: from Biomechanics to Sociodynamics

202