Anomaly Extraction Technique of Airborne Gamma Spectrometry

Based on 2-D Wavelet

Kun Sun, Liangquan Ge*, Fei Li, Meng Wang , Xian Guan ,Yi Gu and Qingxian Zhang

The College of Nuclear Techonology and Autornation Engineering, Chengdu University of Techonglogy, Chengdu 610101,

China.

Email: glq@cdut.edu.cn

Keywords: Airborne gamma spectrometry, 2-D wavelet, anomaly extraction

Abstract: This paper uses 2-D wavelet transform to process the uranium specific activity data of 1:5000 airborne

gamma-ray spectrometry production data in a survey area in Inner Mongolia, and uses the distribution of

paleo-uranium abundance to correct the extracted anomaly areas. The experiment shows that, with small

area and high uranium ore concentration, the anomaly areas extracted by 2-D wavelet method are consistent

with the metallogenic environment. This method also appears to be insensitive to low concentration uranium

areas which may help in guiding for metallogenic prognosis.

1 INTRODUCTION

Airborne gamma-ray spectrometric survey has the

advantages of high detection efficiency, lo w cost,

and covering large areas for surface concentrations

of various gamma emitting radionuclides

(Wan et al.,

2012). At present, 80% of China's uranium deposits

were found by airborne gamma-ray spectrometric

survey (Liu et al., 2002). Due to the low intensity of

airborne gamma-ray spectrometric signals, the

signals caused by ore-bodies are easily comb ined

with other external measurement signals (reflected

informat ion on detector by lithology, soil type,

humid ity, vegetation coverage density, water area

distribution, etc.) (Ge et al., 2016, Xiong, 2016 ),

making it more difficult to extract ano malous areas,

making it more difficult to extract anomaly areas.

The method of e xtract ing anomalous information

fro m airborne gamma -ray spectrometry data is

similar to geochemical data anomalous informat ion

extraction method. In recent years, many scholars

have tried to use wavelet mu lti-scale analysis to

extract anomaly information. Gan Yuan et al.

(2013)used wavelet multi-scale analysis to filter and

denoise wavelet on field X-ray fluorescence

geochemical data

(Gan, 2013). The extracted

anomalous information a reas are s maller than those

extracted by the conventional method and are highly

consistent with actual geological background. Nan

Yan et al. (2017)applied wavelet analysis to

delineate the ano maly limit of geochemical

exploration in the Dabat area of Xin jiang(Nan et al.,

2017). The ext racted anomalous information is

consistent with the spatial distribution of known ore

sites and some extremely weak anomalies were

extracted.

As the airborne gamma-ray spectrometric survey

system is vulnerable to external factors, the collected

usable signals are easily interfered by other signals.

The wavelet t ransform has good time -frequency

characteristics and is good at handling non-

stationary signals. Traditional wavelet analysis

ignores the spatial location informat ion of survey

areas. The 2-D wavelet transform co mb ines the

spatial location information of survey areas with the

element content information, deco mposing the data

and reconstructing the low-frequency part.

According to the reconstructed data, the anomalous

informat ion in the survey area is e xt racted to

improve the accuracy of any anomaly information in

the survey area and reduce the areas of false

anomalies, which provides a basis for aiding in

prospecting.

Sun, K., Ge, L., Li, F., Wang, M., Guan, X., Gu, Y. and Zhang, Q.

Anomaly Extraction Technique of Airborne Gamma Spectrometry Based on 2-D Wavelet.

In Proceedings of the International Workshop on Environment and Geoscience (IWEG 2018), pages 283-287

ISBN: 978-989-758-342-1

283

2 METHODS

2.1 2-D Wavelet

The basic principles of 2-D wavelet used to extract

the anomalous information fro m airborne gamma-

ray spectrometry data are as follows. Let

f( , )

x y L



be a 2-D signal, x, y denote the

horizontal and vertical coordinates, and

（x,y）

denotes 2-D wavelet basis function, then 2-D

continuous wavelet definition is (Daubechies, 2011):

a;b ,b 1 2

( , ) , a 0; ,

x b x b

x y b b R





    





(1)

Where,

a;b ,b

( , )



is a 2-D wavelet

generating function,

is a scaling factor, and

is displacement factors. Let

2 , * ;

a b n a j Z

  

, so 2-D

continuous wavelet transform can be discretized:

 

j;k ,k 1 2

( , ) 2 2 ,2

x y x k x k





    

(2)

So 2-D discrete wavelet transform is:

f 1 2 ; ,

( ; , ) ( , ), ( , )

j k k

WT j k k f x y x y

  

2 ( , ) (2 ,2 )

j j j

f x y x k y k dxdy

  

  



(3)

The simplified formu la for 2-D wavelet

decomposition is as follows:

f( , ) ( , ) ( , ) ( , ) ( , )

H Y D

x y L x y H x y H x y H x y

   

(4)

Where,

( , )

L x y

and

( , )

H x y

( , )

H x y

( , )

H x y

are the approximate components of the

original signal

f( , )

and the detail co mponents

in the horizontal, vertical, and diagonal directions,

respectively.

Anomaly Extraction Technique

2.2 Anomaly Extraction Technique

Differences in wavelet basis functions lead to

differences in the results of different transformat ion

types. It may not be easy to accurately distinguish

the better and less preferable these extracted

anomalous information by naked eye. Therefore, the

standard deviation coefficient of variation

(hereinafter referred to as CV) can be used to

identify whether or not the optimal deco mposition

level has been reached after 2-D wavelet

decomposition.

Since the ore-bearing areas are all in the areas

with high CV

(Sun, 2009), the CV of gamma-ray

spectrometry can reflect the variation degree of the

contents of uranium, thoriu m, and potassium

contents in the survey area. Therefo re, it can be used

to study the spatial distribution of radioactive

elements, as a geological general survey and

prospecting tool.

CV is the ratio o f the samp le mean square error

to the sample mean

(Gilbert and Richardo, 1988). In

the anomaly extract ion of airborne gamma-ray

spectrometry data, the standard deviation CV

(Sun,

2009, Zhang and Xiong, 1990) is used to measure

the degree of data dispersion and to predict

metallogenetic probability. The formula is as follow:

()

n-1









(5)

Where,

is the mean value of an element in the

survey area;

is the total survey points of the

survey area;

is the element content value of a

survey point in the survey area. In a stable

geological structure, the element

content value has small fluctuation range, strong

resistance to external disturbances, and low

CV. With an inho mogeneous geological structure,

the element content value in the ore-bearing

strata has high CV, which is conducive to

discovering ore-causing information.

The 2-D wavelet deco mposition process is: First,

the wavelet decomposition is carried out in the

horizontal d irection of the data matrix; secondly,

decompose the two decomposed sub-bands along

the vertical direction; reconstruct the reconstructed

low-low frequency part and calculate its CV;

identify if there is a mutation in the CV: if it is not

mutated, iteratively deco mpose the low-low

IWEG 2018 - International Workshop on Environment and Geoscience

284

frequency part, and if it is mutated, output low-low

frequency part.

3 RESULTS AND DISCUSSION

3.1 Survey Area

This project selects A GS863 Airborne γ

spectrometry 1:5000 data of Chengdu University of

Technology of a survey area in Inner Mongolia as a

data source for data processing. The geological map

of the survey area is shown in Figure 1. W ith five

4L NaI crystals, the AGS863 is a array NaI detectors

installed in Y-12 aircraft.The aircraft is equipped

with data co llect ion system, rad io altimeter, and

global positioning system. Its flying speed is 250

km/h and the average flying height is 180 m.

AGS863 records a data of full spectrum every

second. Full spectrum measured by γ spectrometry

is shown in Figure 2.

The survey area is approximately 1,000 square

kilometers, with a total of 21 survey lines and 6,705

survey points. The measured data was corrected by

altitude, at mospheric radon, aircraft background, and

cosmic ray background. Use Kriging to interpolate

the original data (256* 256) and draw a contour map

(shown in Figure 3). The h ighest uranium specific

activity value is 37.204(

g

); the lo west value

is 0.049(

g

); the average value is

3.968(

g

Figure 1: Geological map of the survey area.

Figure 2: Actual measured full spectrum.

Figure 3: Uranium specific activity contour map.

Figure 4: Coefficient of variation after decomposition

and reconstruction of different wavelet basis functions.

Anomaly Extraction Technique of Airborne Gamma Spectrometry Based on 2-D Wavelet

285

3.2 Extraction of Uranium Elemental

Anomaly Information

This paper uses 2-D wavelet transform method to

extract anomalies and compares it with the

traditional one. Because the airborne gamma-ray

spectrometry data is discrete, the frequently-used

wavelet basis functions that can be used for discrete

wavelet transform are Biorthogonal (biorNr.Nd),

Coiflets (coifN), Daubechies (dbN), Meyer (mey r)

and ReverseBior (rbioNr.Nd) (the functions in the

modules that contain wavelet basis functions in

MATLAB can directly be called). Use the above

five discrete wavelet basis functions to decompose

and reconstruct the data, respectively, and calculate

the CV of each processed data by formula (5). The

results are shown in Figure 4.

Figure 4 shows that when decomposition level is

the same, the CV of each data possessed by different

wavelet basis functions are quite different. The CV

of data processed by the same wavelet basis function

have a negative correlation with the decomposition

level at level 1-4, and when the decomposition level

is at 5, the CV of the data reaches the maximu m;

when the decomposition level is at 1-4, the change

rate of CV is s mall and the overall trend is relatively

stable, which show that wavelet decomposition has a

small impact on the whole data.

The author uses traditional statistical method and

2-D wavelet method (wavelet basis function is

bior6.8; deco mposition level is at 5) to extract

anomalies from the data and compare the extracted

anomalies. The results are shown in Figure 5.

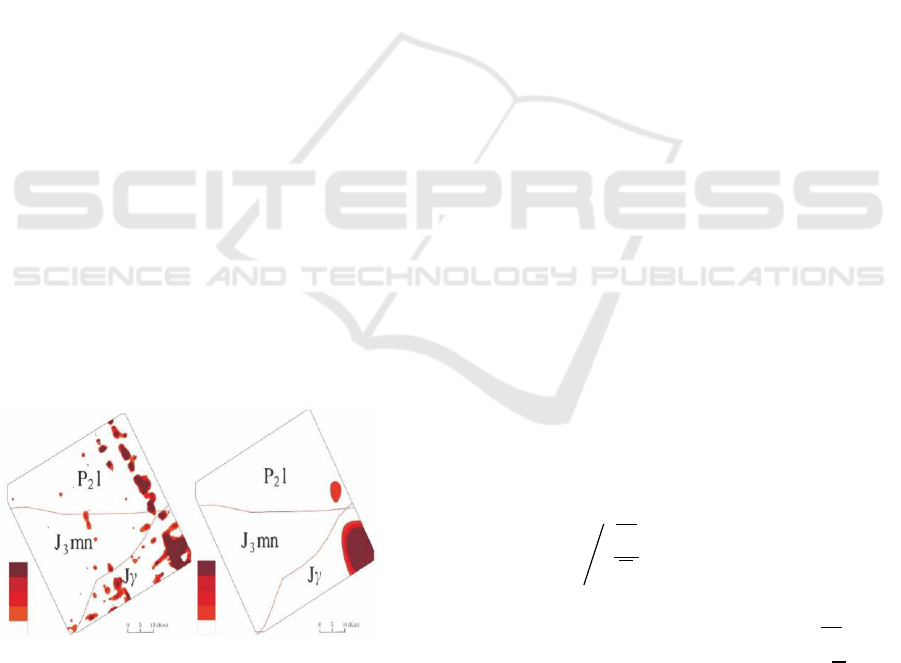
Figure 5(a): Traditional method to extract the

anomaly area. (left)

Figure 5(b): 2-D wavelet to extract the anomaly area.

(right)

As shown in Figure 5(a), the ano malous

informat ion extracted by the traditional statistical

method has a large area, and the banded anomaly

interference in formation is obvious and scattered.

The reason is that the original data does not have an

approximately normal distribution, and the high-

value point data is missing during iterative reject

phase, resulting in the anomaly threshold value

being determined only by the background value.

The advantage of the 2-D wavelet method is that

it can co mbine the element content information of

survey points with the spatial position information;

there are two ore occurrences in the survey area, one

is lead-zinc ore with high U content and one is iron

ore with low U content. In Figure 5(b), there are

only two anomalies. The central location and

anomaly shape of the anomalous areas are consistent

with the actual ore occurrences, indicating that the

results do not contain false anomalies. Since the

low-frequency parts only contain ore-bearing and

background information, and the ore-bearing

informat ion are represented by high value ano malies.

Therefore, the ano maly a reas in the figure may be

ore-bearing areas.

3.3 Verification of Uranium Elemental

Anomaly Information

The paleo-uraniu m abundance refers to the uranium

content of an area in its beginning of diagenesis. In

the initial stage of diagenesis, U and Th have the

same chemical properties and no migration occurs ;

When the later environ ment beco mes an oxidation

environment, U migrates, while the chemical

properties of Th are relatively stable and remain in

place. The uran iu m ano maly areas indicated by

paleo-uraniu m abundance are source beds. Formula

6 is the fo rmula for the calculation o f paleo-uraniu m

abundance(Dai, 2002):

u ( )

G Th



(6)

In formu la (6):

is the thoriu m content of a

certain survey point in the survey area;

is the

average thorium content in the survey area;

is the

average uranium content in the survey area.

Using formu la (6) to calculate the paleo-uraniu m

abundance in the survey area, the result is shown in

Figure 6.

At the beginning of diagenesis, uraniu m is

mainly concentrated in granite. The main lithology

IWEG 2018 - International Workshop on Environment and Geoscience

286

in the southeastern part of the survey area is granite,

with an approximately triangular distribution. Figure

6 shows that the primary uraniu m element is mainly

concentrated in the southeast of the survey area, and

its distribution profile co incides with the profile of

the high uranium value area, indicating that there are

ore-bearing strata in this area and it has meta llogenic

conditions. Therefore, 2-D wavelet processing was

effective at locating ore-bearing units.

Figure 6: Distribution of paleo-uranium abundance.

4 CONCLUSIONS

In order to explore the advantages of 2-D wavelet

method in the extraction of ano malous information

of airborne gamma spectrometry data, comb ined

with the distribution of ancient uraniu m, an ano maly

extraction technique based on two-dimensional

wavelet method was applied to a gamma-ray survey

area. Co mpared with anomaly areas extracted

by traditional method, the anomaly areas extracted

by 2-D wavelet methods were sma ller and have a

more obvious concentration trend. These anomalous

areas were in accordance with the actual ore

occurrences and no false anomalies in the survey

area were detected. The result shows that the 2-D

wavelet methods can effectively extract the

anomalous informat ion fro m airborne gamma-ray

spectrometry, and provide a basis for aiding in

prospecting. However, This method is insensitive to

very weak ano malies . It can only extract ano malous

informat ion and somehow depends on the quality of

the original data, so it needs to be further developed.

ACKNOWLEDGEMENTS

This article was funded by the National Key R&D

Project (No.2017YFC0602105), the National

Natural Science Foundation of Ch ina (No.

41774147) , Sichuan Science and Technology

Support Program (No. 2015GZ0272)and the

Sichuan Provincia l Department of Education

Research Project (No.16ZA0085). Also thanks to

Professor Zhou Sichun, Doc. Xiong chao for his

guidance and opinions.

REFERENCES

Dai J M 2002 Discussion on characteristic Parameters of

gamma-spectrometric data Uranium Geology 1 52-55

Daubechies I 2011 Ten lectures on wavelets National

Defend Industry Press

Gan Y, Ge L Q, Wang Z, et al. 2013 The research of in-

situ XRF geochemical data processing based on

wavelet transform Nuclear Electronics & Detection

Technology 33 103-106

Ge L Q, Xiong S Q, Zeng G Q, et al. 2016 Airborne

gamma-ray spectrum detection and application BeiJing

Science Press

Gilbert and Richardo 1988 Statistical methods for

environmental pollution monitoring Van Nostrand

Reinhold Co

Liu Y H, Gu R K and Hou Z R 2002 Airborne

radiometrics survey Geophysical and Geochemical

Exploration 4 250-252

Nan Y, Lei Z Q, Xu Y, et al. 2017 Application of wavelet

Analysis to determine the lower limit of Geochemical

exploration in the Da bar area Xinjiang Gansu Science

and Technology 33 20-22+3

Sun Z R 2009 Study on usage of coefficient of variation

for statistics of magnetic Parameters of samples

Geology and Prospecting 45 65-69

Wan J H, Xiong S Q and Fan Z G 2012 The status and

prospects of airborne gamma-ray spectrometry

technology and its application Geophysical and

Geochemical Exploration 36 386-391

Xiong C 2016 The research on anomaly information

extraction method of airborne gamma-ray spectrum

survey Chengdu University of Technology

Zhang W B and Xiong S Q 1990 Airborne gamma-ray

Spectrometric variation coefficient—a useful

Parameter for interpretation Geophysical and

Geochemical Exploration 4 276-284

Anomaly Extraction Technique of Airborne Gamma Spectrometry Based on 2-D Wavelet

287