Mechanical Analysis and Structure Optimization of Lunar Soil

Coring Mechanism

Qiuyi Fang

1,*

Qin Zhou

, Jianguo Lv

and Jing Wang

Sergeant school of CAPF; #377 Tianmu Shan Road, Xihu District, Hangzhou, Zhejiang

China University of Geosciences, Beijing; #29 Xueyuan Road, Haidian District, Beijing

Sinomine Resource Exploration

；

#11 Changchunqiao Road, Haidian District, Beijing

Email: fangxiaoqiu@126.com

Keywords: Coring mechanism, mechanical model, bedding information-keeping, structure optimization

Abstract: The soft bag lunar soil coring mechanism of turning inward type without sliding has the characteristics of

simple structure, low power dissipation and well regolith bedding information-keeping. However, at the

initial coring stage, the large pulling force and torque, which are resulted from the spiral movement of lunar

soil around bit when it enters the holding-pipe, can consequently cause high power dissipation and bad

regolith bedding information-keeping. In the paper, in order to achieve the goal of the minimum of pulling

force and torque, a mechanical model representing the interaction of lunar soil on coring mechanism was

established to analyze effects of structural parameters and drilling parameters on the pulling force and

torque. The structural parameters of coring mechanism and drilling parameters were optimized. The results

show that soft bag thickness and guide head radius have the greater impact on the pulling force and on the

torque respectively. When the guide head radius is 0.5mm and the soft bag thickness is 0.2mm, the rope

pulling force can reach its optimal value of 89N, which can greatly reduce the degree of torsion in the

process of coring.

1 INTRODUCTION

Probing the moon’s material composition has great

significance on studying the origin of the moon and

the earth, the earth's climate, and the phenomena of

tidal waters. Drilling and sampling the surface of the

moon are prerequisite for achieving this research

work (Yan et al., 2004).

There have been some successful sampling

precedents of lunar soil abroad, however, coring

methods and working mechanism of deep lunar soil

coring domestically are still staying at theoretical

and experimental research stage. In the Apollo

program, for example, the core was extracted using a

cemented carbide tube (The Apollo 17 mission” on

http://spaceflight1.nasa.gov/history/apollo/). This

device for sampling cores was easily operated but

with poor bedding information (Berry, 1970). In the

Luna24 program, the soft bag coring mechanism of

turning inward type was initially applied and the

core of 250cm depth can be successfully extracted

with good bedding information-keeping

(http://www.zarya.info/Diaries/Luna/Luna.php). Due

to its good performance, such a turning inward type

device will be a great potential, which is well worth

being researched (Zhang, 2010). Some domestic

scientific research units, such as Beijing Satellite

Manufacturing Factory, Harbin Institute of

Technology and China University of Geosciences,

are also carrying out some researches (Duan et al.,

2009). In terms of mechanical model, the mechanics

characterizes of the drill (Li, 2012), the bit 0 Tang,

2012) and other structural joints have been mainly

analyzed (Liu, 2011). The interaction among the

inner parts of the core body, such as the soft bag, the

holding-pipe, the drill rod and the lunar soil, in the

drilling process is rarely analyzed. Little information

is available. In the analysis of lunar soil coring

mechanism mechanics characterizes,Wang Guoxin

and others, from Beijing Satellite Manufacturing

Factory,using a simplified mechanical model, has

not considered the influence of the speed when soft

bag turning in (Zhao et al., 2012). The effect of soft

bag turning on regolith bedding information-keeping

was not analyzed either (Wang, 2012). Although the

researchers of Harbin Institute of Technology have a

comprehensive study on the coring mechanism, the

influence of the structural parameters and drilling

parameters on sampling is not studied

Fang, Q., Zhou, Q., Lv, J. and Wang, J.

Mechanical Analysis and Structure Optimization of Lunar Soil Coring Mechanism.

In Proceedings of the International Workshop on Environment and Geoscience (IWEG 2018), pages 533-540

ISBN: 978-989-758-342-1

533

simultaneously (Gong et al., 2012). Especially in the

initial stage of coring, the interaction among soft

bag, lunar soil and coring mechanism is the most

complex, which few studies have ever researched

before.

In view of the above research, this paper carries

out the mechanical model of the coring mechanism

in the initial sampling stage and optimized of the

core mechanism. Taking the minimum of the sample

load and the torque as the optimization objective, the

structure parameters and the drilling parameters are

used as variables, then using the control variable

method to analyze and get the optimal value.

2 THE COMPOSITION AND

WORKING PRINCIPLE OF

CORING MECHANISM

The coring mechanism mainly consists of hollow

coring tool, drill bit, holding-pipe, soft bag, rope,

sealing components and other appendages. Figure

1is the structure diagram.

The soft bag is installed outside the holding-pipe,

which is screwed inside the hollow rod through

thread. When sampling, with the drill feeding, soft

bag turns inward and wraps the soil gradually. The

sample pushing into the soft bag with soft bag

remains relatively stationary. After drilling, we can

get a cylindrical lunar soil core wrapped by soft bag

inside the holding-pipe.

Figure 1: Structure diagram of coring mechanism.

Figure 2: The interaction relationship between lunar soil

and coring mechanism.

In the initial stages of drilling, due to the soil-

breaking perturbations by drilling and the spacing

between drill and holding-pipe, the lunar soil around

the drill bit into the holding-pipe as the way of a

spiral motion. Under the disturbance of lunar soil

movement and the lateral pressure that lunar soil

entering the coring mechanism on the soft bag, the

resistance of soft bag turning inward and the trend of

soft bag twisting are increased. The interaction

relationship between the bit, lunar soil and coring

mechanism in this stage is shown in Figure 2.

Therefore, the force condition of soft bag around

guide head is the key to affect the quality of

sampling and the power dissipation.

3 MECHANICAL MODEL

REPRESENTING THE

INTERACTION BETWEEN

LUNAR SOIL AND CORING

MECHANISM AROUND THE

GUIDE HEAD

Now suppose that the guide head has ideal structures

and the soft bag is an absolutely flexible mechanism,

which works as belt driving (Gong et al., 2012).

Around the guide head, the soft bag is divided into

circumferential infinitesimal and tangential

infinitesimal to make the analysis on the internal and

external forces. The forces like tangential tension of

infinitesimal T(α), the frictional resistance of

infinitesimal F

and the circumferential tensioning

force of infinitesimalT

(α)are shown in Figure 3 and

Figure 4. The force equilibrium equations of soft bag

were established (Wang, 2012; Cao and Gu, 2004).

Figure 3: Infinitesimal radial force of soft bag.

IWEG 2018 - International Workshop on Environment and Geoscience

534

Figure 4: Infinitesimal circumferential force of soft bag.

The circumferential infinitesimal width of center

angle dθ corresponds to the one of soft bag; the

tangential infinitesimal can be obtained by

continuously dividing the circumferential

infinitesimal on length,which corresponds to the

length of center angle dα.Then the soft bagsurface

infinitesimal ds can be got. According to the

derivation of Euler's formula, the dynamic

equilibrium equation of ds was established (

Cao

and Gu, 2004)

3.1 The Dynamic Equilibrium

Equations of Infinitesimal

The radical and tangential force balance has been

analyzed and expressed as equation 1:

()

ττ

ma)dN(f

cosT

cosdTT:0F

−+⋅+⋅=⋅+=

∑

(1)

()

nnn

madN

sinT

sindTT:F ++=⋅+⋅+=

∑

(2)

Let

NdN

sin

=⋅

cos

=⋅

Based on the limit principle, we can get:

cos ~ 1,sin ~ ,sin ~ sin ,cos ~ cos

222 2 2

ddd d d

ααα α α

αααα

⎛⎞ ⎛⎞

⎜⎟ ⎜⎟

⎝⎠ ⎝⎠

Substituting them into equation (1) and (2), it

gives:

NTd ma

=⋅ −⋅ (3)

dT f N m a

=⋅−⋅ (4)

From the equation above, the relationship among

tangential tension of infinitesimal can be got, the

angle of guide head and the radial and tangential

acceleration of soft bag:

()

dT f T d m a m a

=⋅ ⋅ −⋅ −⋅

(5)

Among them,

()

mRd

=⋅ ⋅

(ρ is the linear

density of soft bag(axial direction)).

By dividing d

on both sides of the equation, we

can get:

()

Td Ra Ra

αρ ρ

=⋅ ⋅ − −

(6)

According to the boundary conditions when soft

bag turning inward, we can get soft bag tension

boundary value in the infinitesimal direction,

namely:

When

()

0 TF

==，

, the friction between soft

bag and the outside wall of holding-pipe;

When

()

απ

==，

, the pulling force of

rope.

In the integral form of (6):

fe F Ra Ra Ra Ra

ττ

ρρρρ

⎛⎞

⋅− −⋅ + +

⎜⎟

⎝⎠

(7)

is the friction between soft bag and the outside

wall of holding-pipe;

The formula (7) provides a theoretical basis for

mechanical analysis of soft bag turning inward. It

shows the dynamic relationship between the pulling

force of rope and the wrap angle of soft bag, with

the acceleration of soft bag’s movement, and gives

the quantitative relationship among force, friction,

the radius of guide head and the linear density of

soft bag intuitively.

3.2 The Mechanical Model of Pulling

Force of Soft Bag Turning Inward

at the Initial Stage

In the initial stages of drilling, due to the soil-

breaking perturbations by drilling and the spacing

between drill and holding-pipe, the lunar soil around

the drill bit verb into the holding-pipe as the way of

a spiral motion. Relative to the smooth transition of

coring, the resistance of soft bag overturning

increases. The friction is relatively the largest during

the process of coring. At the same time, because of

the soft bag with a maximum acceleration in this

stage, the external force that needed is greater as

well. Based on the analysis above, the forces of the

soft bag at this stage are the most complicated, the

mechanical analysis of the stage is representative.

The following will give the unfolding calculation

of the formula(7), to provide a basis for optimizing

the coring mechanism by analyzing the pulling force

of rope’s mechanical relations between structural

parameters of coring mechanism, drilling parameters

and physical characteristics of lunar soil.

(1) Calculate the radial tightening force of soft

bag

The formulas and relations between the radial

tightening force and the circumferential tensioning

force are expressed as follows:

Mechanical Analysis and Structure Optimization of Lunar Soil Coring Mechanism

535

⎪

⎩

⎪

⎨

⎧

⋅=

−

⋅⋅=

⋅=

bdlA

AET

sinTF

(8)

A. In the guide head, the radial tightening force

of soft bag:

()

22 cosddRR d

αα

=++⋅ +

(9)

Therefore:

()

21cos

EbR d

Tdl

FTd

αα

⎧

⋅+ +

⎡⎤

⎣⎦

=⋅

⎪

⎨

⎪

=⋅

⎩

(10)

()

,cos

dN F

θα α

⎛⎞

=⋅ +

⎜⎟

⎝⎠

(11)

B. Outside the holding-pipe, the radial tightening

force of soft bag:

()

Eb d d

Tdl

FTd

⎧

⋅−

=⋅

⎪

⎨

⎪

=⋅

⎩

(12)

()

dN F

θα

(13)

Therefore, the maximum radial tightening force

of infinitesimal is:

() () ()

,,,dN dN dN

θα θα θα

cos

⎛⎞

=⋅ + +

⎜⎟

⎝⎠

(14)

()

[]

dld

)dd(bE

dldd

)

),(N

01L

cos1R2d

⋅

−⋅

+⋅⋅

+⋅

∫∫∫∫ ∫

⋅+−⋅

θθα

αθ

απ

cos(1bR2E

()

11 10

BR d R Bd x B x d d

⎛⎞

=−+Δ= Δ=−

⎜⎟

⎝⎠

(15)

Integrating the force in the axial direction, can

get the total radial tightening force of soft bag N (z):

() ( )

Nz BR d R dz Bd xdz

=⋅−⋅+⋅Δ⋅

∫∫

()

Rd R BdLx

=−+⋅Δ

(16)

(2) Calculate the lateral pressure σ

of the lunar

soil

The lateral pressure σ

of the lunar soil at any

depth can be equivalent to the earth pressure at rest,

and σ

is proportional to its self-weight σ

, which

can be expressed as (Chen et al., 1994):

σσ

=⋅ (17)

Where,

—Coefficient of earth pressure at rest, the

relations between k

and internal friction angle of

lunar soil approximated as (Zhang, 2000):

1sink

=−

— The gravity stress of lunar soil,

()

az zdz

σπ ρ

−

=⋅ ⋅ ⋅

∫

(In which,

()

— The spontaneous stacking

density of lunar soil (Qin, 1998),

()

1.92 12.2

zgcm

is the best estimate;

a —The gravitational acceleration of Moon (Zheng

et al., 2004),

a =

;)

Substituting them into the formula of σ

calculate the gravity stress of lunar soil:

()

() ()

⎥

⎦

⎤

⎢

⎣

⎡

−+−+⋅+⋅−=

18z

18zln2.1218zlnz2.12zR4dg80

πσ

(18)

Since this is a mechanical analysis for soil-

breaking critical state when drilling, the value of

can be simplified as:

()

16.74 4

dRg

σπ

=⋅−⋅

() ()()

1 sin 16.74 1 sin 4

σϕσπϕ

=− ⋅ = − ⋅ −

(19)

(3) Calculating the pulling force

The total pressuresthat soft bag roleson holding-

pipe is the sum ofthe radial tightening force and the

lateral pressure of lunar soil:

()

NNz

()

011

kBRdRBdLx

=⋅+ ⋅ − + ⋅Δ (20)

Then the maximum static friction force of soft

bag turning inward in the initial stage can be got:

fN=⋅

() ( )()

[

]

111

R4dsin1g74.16xLBdR4dBRf −⋅−+Δ⋅+−⋅⋅=

ϕππ

(21)

Substituting (21) into (7) gives the pulling force

of rope F

() ( )()

ττ

ρρρρϕππ

RaRa

RaR4dsin1g74.16xLBdR4dBRfeF

111

⎥

⎦

⎤

⎢

⎣

⎡

−−−⋅−+Δ⋅+−⋅⋅=

(22)

Equation (22) gives a calculation formula of

pulling force of rope in the initial stage. This also

links the pulling force with structure parameters and

drilling parameters.

IWEG 2018 - International Workshop on Environment and Geoscience

536

3.3 Analytical Model of Soft Bag

Torque

At the beginning of coring, the lunar soil entering

the soft bag has acircular motion tendency. Under

the effect of sliding friction force, which was caused

by the lunar regolith and soft bag, soft bag will come

about twisting phenomenon. This will affect the

bedding information of sampling. For the

phenomenon above, building the analytical model of

soft bag torque is of great significance for

optimizing the structural parameters of coring

mechanism (Fei et al., 2008)

(1) Calculate the torque T

is generated bythe radial tightening force of

soft bag and the centripetal force of ROP. The

infinitesimal torque generated by the radial

tightening force of infinitesimal is:

Calculate centripetal force:

()

Vd Rd

=⋅⋅⋅⋅

(23)

Where, F

is the radial tightening force of soft

bag in guide head. The tangential friction F

that

aroused by the centripetal force and the radial

tightening forceoutside the holding- pipe wall can be

expressed as:

()

FfFF=⋅ +

(24)

The torque caused by F

can be expressed as:

TF=⋅

() ( )

22 2

Vd Rd BR d R

πρ απ

⎡⎤

=⋅ ⋅⋅+ ⋅−

⎣⎦

(25)

Integrating the torque, the total torque generated

by the radial tightening force of soft bag can be got:

()

222

11 1 1

Tfd BRdR VdRd

⎡⎤

=⋅ ⋅− + ⋅ ⋅

⎢⎥

⎣⎦

∫

()

232

11 1

dBRdR VdR

⎡⎤

=⋅ ⋅− +⋅

⎢⎥

⎣⎦

(26)

(2) Calculate the torqueT

The sliding friction force, which produced by the

lunar regolith and soft bag, can be expressed as:

yr n

=⋅

() ()

= 1 sin 16.74 4

dRg

μϕπ

⋅− ⋅ ⋅ − ⋅

(27)

(



: The friction coefficient between lunar soil

and soft bag)

To make the central axis of holding-pipe as the

axis, the torque T

is generated by F

as follow:

TF⋅

() ()

1 sin 16.74 4

dRg

μϕπ

=⋅− ⋅ ⋅− ⋅⋅ (28)

(3)Calculate the total torque T

The algebraic sum of T

and T

is the total

torque:

TTT=+

() ()()

gR4dsin_17.16RdVR4dBR

1yr1

⋅⋅−⋅⋅⋅+

⎥

⎦

⎤

⎢

⎣

⎡

⋅+−⋅⋅=

ϕμπρπ

(29)

The value of torque will represent the extent of

soft bag twisting directly, the smaller of T, the more

conducive to coring, and vice versa. The parameters

that influence T are given by formula (29), such as

ƒ, E

, b, d

, L, d

, V

4 ANALYSIS OF THE

INFLUENCE OF PARAMETERS

ON PULLING FORCE AND

SOFT BAG TORQUE

The analysis of regression of the dynamic model has

been made to figure out the law representing the

influence of structural parameters on the soft bag

torque and the hauling cable pulling force. Then the

structural parameters of the simulation coring

mechanism have been optimized to achieve the goal

of minimizing the resistance force of the soft bag

when overturning and the torque T.

Based on the models of F

and Torque:

,,,,,,,,,

,,,,,, ,

lyrn

ERbdL aa

fERbd V

ϕρ

ϕμ

⎧

⎛⎞

∝

⎪

⎜⎟

⎝⎠

⎪

⎨

⎛⎞

⎪

∝

⎜⎟

⎪

⎝⎠

⎩

The parameters of , , , 



,,



will be

analyzed through numerical simulation. When in

different drilling rates, the corresponding

accelerations of soft bag in critical states can be

obtained in experimental data. (Let the friction angle

of lunar soil is 40°, friction coefficient between

soft bag and lunar soil is 0.75 (Slyuta, 2014), the

value of drilling depth is 0m, elastic modulus E

around 17.8Gpa, linear density

is 100g/m (Wang

et al., 2001).)

Based on the spatial constraint condition of the

coring mechanisms used in China third lunar

exploration project and the drilling parameters of

Luna-24 used in former Soviet, the constraint

condition of basis data can be expressed as follows:

Mechanical Analysis and Structure Optimization of Lunar Soil Coring Mechanism

537

0.15 1

0.5 2

0.171 0.385

14.5 23

0.3 4

10 20

5/min 50/min

60 / min 500 / min

mm b mm

mm R mm

mm d mm

mm x mm

mm L mm

cm V cm

rVr

≤≤

⎧

⎪

≤≤

⎪

≤≤

⎪

≤≤

⎪

⎨

≤Δ ≤

⎪

≤≤

⎪

≤≤

⎪

≤≤

⎩

Using the method of regression analysis, a goal

function with different ranges has been obtained

within differentparameters. In order to ensure that

the impact of the parameters on the objective

function is comparable, when the objective function

is changed in the range of the corresponding

parameters, the values of the other parameters are

not optimized.Influence of various parameters on the

tension F

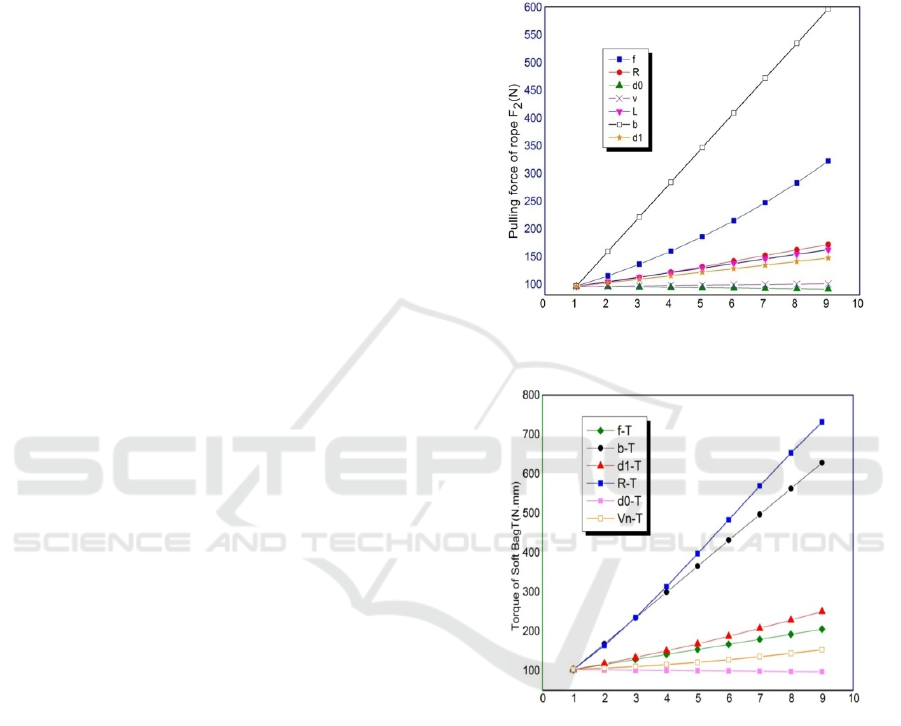
(1) The influence of parameters on F

It shows that F

(s) is related to f, R, b, d

, L, d

Specially, the value of F

has a compound

relationship with f, d

and the fillet radius R. Unlike

guide head radius R, the parameters of b, L, a

and

are proportional to F

. Figure 5 plots the

relationship between different parameters and the

pulling force of rope.

The results show that the greatest varying range

of F

occurs at the range of soft bag thickness, at

which the varying ranges of f, b and d

will decrease.

In addition, d

has the least influence on the range of

(2) The influence of parameters onT

The function of T(s) shows the relations between

torque T and f, b, d

, d

, b and V

. Among them,b is

proportional to T in linear relationship. In addition,

is inversely proportional to T. Figure 6 shows the

relationship between different parameters and the

torque of soft bag.

The results show that the greatest varying range

of T occurs at the direction of the fillet radius, at

which the varying ranges of f, b and d

will

successively decrease. In addition, d

has the least

influence on the range of T.

(3)The optimization of structural parameters and

drilling parameters

By the analysis above, the influence of different

factors on the objective function is at different

levels,the results show that the structural parameters

of coring mechanism and the drilling parameters

have a certain proportion of influence on both

pulling force of rope and soft bag torque, which

should be paid an equal attention on design and

optimization.

Based on the results above, the values of the

parameters of f,R,b,d

,and L will decrease with the

increasing d

, which benefits for coring. Therefore,

when the values of structural parameters and drilling

parameters are taken the optimal values, as shown in

Table 1, the coring mechanism optimized.

Figure 5: The relation curve between the structure

parameters and the objective function F2.

Figure 6: The relation curve between the structure

parameters and the objective function T.

Note: In Figure 5 and Figure 6, the coordinates of

the X axis are equal to eight aliquots for each

parameter.

In practice, we need to balance the various

parameters according to the working conditions and

constraints. We can further verify the optimization

results with the experimental results, then to adjust

the optimization scheme.

IWEG 2018 - International Workshop on Environment and Geoscience

538

Table 1: The value of structural parameters and drilling

parameters before and after optimization.

Parameters Un-

timized

Optimized

The friction coefficient of

soft bag and Holding-pipe

·f

0.296 0.171

Guide head radius·R/mm

1.5 0.5

Soft bag thickness·b/mm

0.75 0.15

Holding-pipe

outerdiameter·d

/mm

23 15

The length of nested

segment soft bag·L/mm

15 10

Soft bag diameter at

natural state·d

/mm

20 14

Penetration

rate·V(mm/min)

500 80

Revolution

rate·V

(r/min)

120 60

Note: The un-optimized value comes from the experiment

when the coring mechanism was taken to verify the

feasibility.

5 CONCLUSIONS

1. The influences of structural parameters and

drilling technology on coring mechanism at the

critical state of static-motion have been

comprehensively analyzed in this paper. The

mechanical model has been established representing

the force at the beginning between soft bag

overturning and lunar soil. In other words, a

dynamic equation has been established to represent

the overturning movement of the soft bag and a

torque model representing.

2. Based on results of the proportion of influence

of different factors on pulling force and torque, it

shows that the soft bag thickness is the most

influential factor on pulling force, and guide head

radius is the most influential factor on torque.

Among the factors of drilling technology, drilling

rate has little influence on pulling force while the

revolution rate has greater influence on soft bag

torque.

3. The conclusion can be achieved after

optimizing the mechanical model: When the s guide

head radius is 0.5mm, soft bag thickness is 0.15mm,

holding-pipe outer diameter d

is 15mm and soft bag

diameter at natural state d

is 14mm, the energy

consumption is lower and sample bedding is better.

LIST OF SYMBOLS

: Holding-pipe

outer diameter

(α): Infinitesimal

circumferential

tensioning force

: Rope diameter

: The angle between

infinitesimal and the axis

: Soft bag

diameter at natural

state

: Infinitesimal

frictional resistance

b: Soft bag thickness

: Lunar soil lateral

ressure

s: Holding-pipe

thickness

()

: The radial

tightening force of soft

R: Guide head radius

:The linear density of

soft bag(axial)

L: The nested

segment length of

soft ba

: The circular elasticity

modulus of soft bag

V , V

: Penetration

rate, revolution rate

: The wrap angle of soft

around

uide hea

A: Cross-sectional

area of infinitesimal

: Coefficient of earth

ressure at

est

: Tangential

acceleration of soft

ag movement

: The gravity stress of

lunar soil

: Radial acceleratio

soft bagmovement

()

: The spon

stackin

densit

of lunar s

),T(

)+dT: Infini

tangential tension

a: Gravitational accelera

Moon

REFERENCES

“Exploring the Moon - Luna 15 through Luna 24” on

http://www.zarya.info/Diaries/Luna/Luna.php

“The Apollo 17 mission” on

http://spaceflight1.nasa.gov/history/apollo/

Berry, R. L. 1970 AIAA Aerospace Sciences Meeting, New

York 02 19-21

Cao Zhujia and Gu Zhanshan 2004(12) Application of

Euler's formula in mechanical design [J] Machinery

Manufacture 2 10-11

Chen Zhongyi, Zhou Jingxing and Wang Hongjin 1994

Soil mechanics[M] Beijing: Tsinghua University Press

12 196-199

Duan Xinsheng, Yan Taining, Gu Xiang, Duan Suhao

2009(11)

Elementary analysis on one of the possible

drilling and sampling techniques for China Lunar

exploration project [J] Geological Science and

Technology Information 28(6) 125-128

Fei Xuebo, Huang Chunming and Chen Naili 2008

Theoretical Mechanics[M] Higher Education Press 10

194-197

Mechanical Analysis and Structure Optimization of Lunar Soil Coring Mechanism

539

Gong Xu, Wang Qingchuan, Zeng Ting, et al. 2012

Chinese Society of Astronautics deep space

exploration[N] Technical Committee of the Ninth

Annual Conference Proceedings 12 910-917

Li Liangliang. Research on evaluation of lunar soil

drilling-sampling characteristics and influence factors

[D] Master Degree thesis of Harbin Institute of

Technology 2012(07)

Liu Fei. Research on drilling-sampling performance based

on interaction model between drill and lunar soil [D]

Master Degree thesis of Harbin Institute of

Technology 2011(06)

Qin Zhihai 1998 Soil Mechanics and Foundation [M]

Beijing: China Water&Power Press 12 110-119

Slyuta E N 2014 Solar System Research 09(48) 330-353

Tang Tingwu.

Optimization Of structure parameters of

sampling core drill for deep Lunar soil [D] Master

Degree thesis of Harbin Institute of Technology

2012(07)

Wang Bin, Jin Zhihao, Qiu Zheming and Liu Mu 2001

Experimental study of Basic properties of PBO

organic fiber [J] Journal of Xi’AnJiaotong University

11 (35) 11

Wang Guoxin 2012 Chinese Society of Astronautics deep

space exploration[N] Technical Committee of the

Ninth Annual Conference Proceedings 12 978-986

Yan Taining, Bu Jiawu, Wu Xiang, Wang Rongjing

2004(12) Difficulties and key technologies of Lunar

drilling and sampling[J]

Geological Science and

Technology Information 23(4) 12-15

Zhang Yu. Research on the key technologies of drilling-

sampling system of slide-type for lunar soil[D] Master

Degree thesis of Harbin Institute of

Technology,2010(06)

Zhang Zhenying 2000 Rock and Soil Mechanics[M]

Beijing: Tsinghua University Press 12 151-153

Zhao Zeng, Meng Weijie, Wang Guoxin, Li Jun 2012

Chinese Society of Astronautics deep space

exploration[N] Technical Committee of the Ninth

Annual Conference Proceedings 12 896-902

Zheng Yongchun, Ouyang Ziyuan, Wang Shijie, Zou

Yong-Liao. Physical and mechanical properties of

lunar regolith Mineral Petrol,2004(12), 24(04): 14-19

IWEG 2018 - International Workshop on Environment and Geoscience

540