
Simulation of Compression Properties of Pyramidal
Sandwich Panels of TC4 Titanium Alloy
H Wang
1
, K X Zhao
1
, B Zhao
2
, X R Chu
1
and J Gao
1, *
1
School of Mechanical, Electrical&Information Engineering, Shandong University,
Weihai, Weihai 264209, Shandong, China;
2
Beijing Aeronautical Manufacturing Technology Research Institute, Beijing 100024,
China
Corresponding author and e-mail: J Gao, shdgj@sdu.edu.cn
Abstract. As a functional structural material, the mechanical properties determine the
application of three-dimensional lattice structure. The panel thickness, core plate thickness,
ribs width, and unit size affect the mechanical properties of the pyramid lattice structure. In
this work, to give guidance for the design of pyramid lattice structure, the influences of the
above factors were studied through numerical simulation.
1. Introduction
As a new type of sandwich material, the key consideration of three-dimensional lattice structure in its
application is the mechanical properties. The static characteristics of three-dimensional lattice
structures mainly include flat compression, shear and bending. According to the experimental results,
the failure mechanism mainly includes panel wrinkling, core buckling and joint shedding and so on.
The mechanical properties of 6061 aluminum alloy tetrahedron lattice structure are tested by
Kooistra [1]. It is proved that the lattice structure of aluminum alloy tetrahedron is superior to that of
aluminum foam. In order to improve the stability of nodes, Queheillalt [2] proposed a pyramid
structure with node plane. Xue [3] and Yungwirth [4] have studied the ability of impact resistance of
three-dimensional lattice structure. It is pointed out that the energy absorption characteristics of
lattice structures are better than that of honeycomb structures when the impact energy is high. Bele [5]
and Bouwhuis [6]
used finite element simulation to optimize the molding process for aluminium
alloy pyramid core, and optimized the forming process. Numerical simulation is carried out to study
the free vibration problems of AISI 304 stainless steel sandwich beams with pyramidal truss core by
Lou [7] and the results are compared with theoretical solutions, it is found that theoretical solutions
agree well with numerical results. The vibration characteristics of the composite pyramidal truss core
sandwich plate with multiple piezoelectric actuator/sensor pairs were examined in the study by Li et
al.[8] Founded that the vibration level of the composite pyramidal truss core sandwich panel can be
effectively suppressed through the proposed piezoelectric actuator/sensor pairs using the velocity
feedback control and LQR control methods.
Wang, H., Zhao, K., Zhao, B., Chu, X. and Gao, J.
Simulation of Compression Properties of Pyramidal Sandwich Panels of TC4 Titanium Alloy.
In Proceedings of the International Workshop on Materials, Chemistry and Engineering (IWMCE 2018), pages 107-114
ISBN: 978-989-758-346-9
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
107

In this work, in order to give guidance for the design of the pyramid lattice structure, the
influences of panel thickness, core plate thickness, ribs width, and unit size on the compression
properties were studied numerical simulation.
2. Numerical simulation of compression properties
Pyramid lattice is a periodically distributed truss structure. The single-core modelling is used for
numerical simulation because the force condition of each core unit is the same when a uniform
pressure load is applied.
2.1. Introduction of numerical model
Figure 1. Pyramid pressure model assembly drawing.
The numerical model of the pyramidal structure for flat press is shown in Figure 1. The core height
(including upper and lower panels) is set to 15mm. The tie constraint is used between the core and
the upper and lower panels. The lower panel is subjected to a complete fixed constraint. The upper
panel is controlled by displacement, other degrees of freedom are restricted and the down press
forming process is completed through the displacement of Z direction. The tangential friction
coefficient was set to 0.36. The density of TC4 sheet is 4.4g/cm
3
, the Poisson's ratio is 0.34, the
elastic modulus and plastic data are obtained by tensile test at room temperature. The elastic modulus
of the material is 109715 MPa.
2.2. Pyramid structure relative density calculation
The
relative density of the lattice structure refers to the ratio of the volume of the core material to the
volume of space it occupies. For the nodal depressing process, the formed core does not have a
regular geometry due to the non-uniformity of the material flow. Therefore, the calculation of relative
density will be based on the geometric parameters of pre-formed panels before forming, as shown in
Figure 2.
Figure 2. Pre-formed panels geometry figure.
IWMCE 2018 - International Workshop on Materials, Chemistry and Engineering
108

The area in the black wireframe shown in Figure 2 is unique to a pyramidal unit, and the nodes in
the red wireframe are shared by four units. So the volume of core material is:
=
2
2
4
D2
(1)
Where, w is rids width and R is the radius of the circular corner, D is the unit size and t
2
is the
thickness of the sheet metal.
Simplified the formula, it can be obtained:
=
82
2
4
(2)
The volume of the formed core is:
=4D
(3)
Where, D is the unit size and h is the core height.
Therefore, the formula of relative density of pyramid structure is as follows:
̅ =
(4)
2.3. Influence of structural parameters
2.3.1. Influence of Panel thickness. To study the panel thickness t
1
influence, core plate thickness t
2
,
the ribs width w and the unit size D are set to 2mm, 4mm and 20mm, respectively. The simulation
results with different panel thickness of 0.5 mm, 1 mm, 1.5 mm and 2 mm are shown in Figure 3.
Figure 3. Failure process of flat pressure and its load-displacement curve.
As shown in Figure 3, the compression process of the pyramid lattice structure can be divided into
four stages: (a) resistance to deformation, (b) buckling instability, (c) contact strengthening and (d)
densification. Corresponding to this, the flat pressure load also presents the four obvious stage
characteristics: firstly, before point a, the truss is stable and the load increases linearly (stage 0 to a);
secondly, the first plastic hinge appears at point a, truss rod buckling instability appears and the load
begins to decrease (stage a to b); thirdly, when the panel presses down to point b, the plastic hinges
contacts with the upper panel, the flat pressure load rises again, with the press continues, the plastic
hinges contacts with the lower panel, and the press load continues arising (stage b to c); finally, after
point c, the truss is completely destroyed, a large number of trusses contact with the panel occurs
which leads to the densification stage and the flat compression load increases further.
Simulation of Compression Properties of Pyramidal Sandwich Panels of TC4 Titanium Alloy
109
Usually the lattice structural failure occurs when the truss undergoes plastic yield instability and
the corresponding strength is compressive strength. The equivalent flat compressive strength formula
can be defined as:
σ=
(5)
Where, F is the peak load of plastic yield instability, D is the unit size.
The formula for calculating the equivalent modulus of flat compression is as follows:
=
⁄
(6)
Where, δ is the pressing height of linear stage and h is the original lattice height. According to
numerical simulation results and the formulas (5) and (6).
The equivalent flat compressive strength and modulus under different panel thickness are obtained
as shown in Table 1. As the thickness of the panel increases, the equivalent flat compressive strength
and modulus of the pyramidal element decrease. This is because under the condition of constant
height, the panel thickness increases and the truss rid tilt angle decreases, resulting in a reduction in
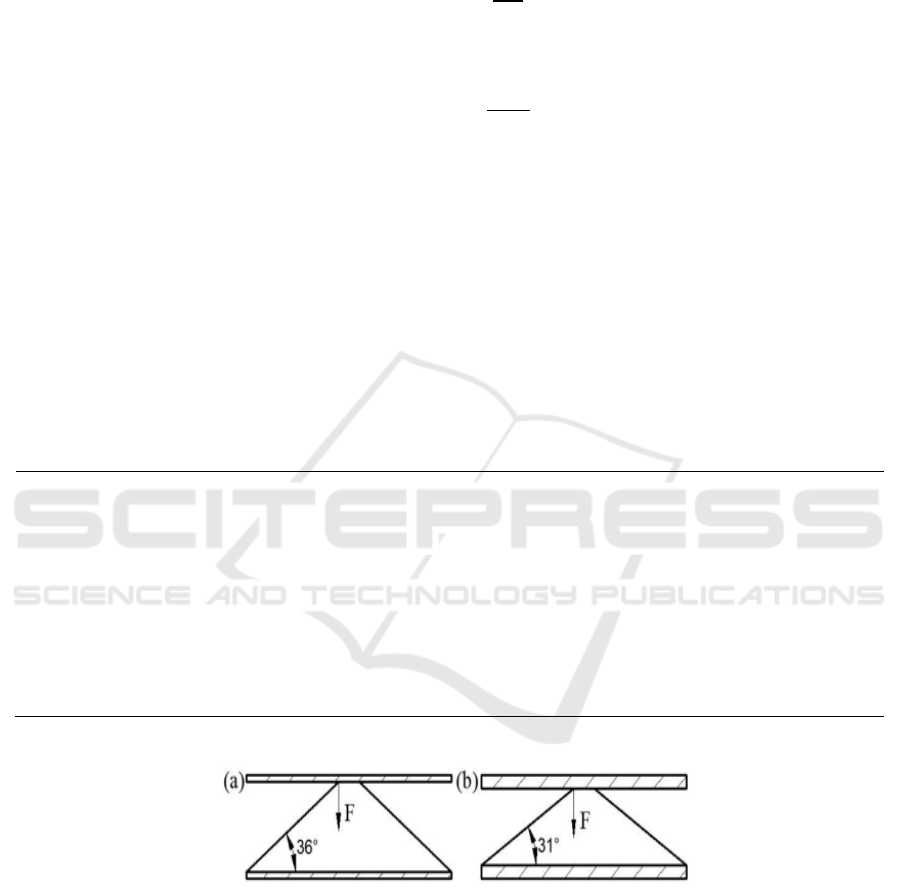
the ability of the truss rid to resist vertical downward loading. Figure 4 is the comparison of tilt
angles of truss rods for panel thicknesses of 1mm and 2mm. The larger tilt angle makes the core unit
with a panel thickness of 1 mm more efficient, resulting in a greater equivalent compressive modulus
with a lower relative density, indicating that by increasing the tilt angle, the compression
performance of the pyramid lattice can be improved.
Table 1. Equivalent flat compressive strength and modulus under different panel thickness.
Panel thickness(mm) 0.5 1 1.5 3
Relative density (%) 2.60 2.80 3.03 3.31
Equivalent flat compressive strength (MPa) 8.44 7.93 7.45 6.86
Equivalent flat compressive modulus (MPa) 379 339.9 268 209.86
Strength-to-density ratio(MPa) 3.25 2.83 2.46 2.07
Modulus-to-density ratio(MPa) 145.77 121.39 88.45 63.40
Figure 4. Effect of panel thickness on tilting angle of truss rid (a) t
1
=1mm, (b) t
1
=2mm.
2.3.2. Influence of Core plate thickness. The thickness of the panel t
1
, the width of the ribs w, and the
unit size D are set to 1mm, 4mm, 20mm, respectively and the thickness of the core plate is taken as
0.6mm, 1mm. 1.5mm, 2mm to study the influence of the core plate thickness.
IWMCE 2018 - International Workshop on Materials, Chemistry and Engineering
110

Figure 5. The influence of core plate thickness on the process of flat compression (a) t2=2mm, (b)
t2=0.6mm.
Figure 6. Simulation of load-displacement curve under different core plate thickness.
Figure 5 shows the comparison of stresses states during the pressing process when the core plate
thickness is 2mm and 0.6mm. It can be seen that changing the core plate thickness will affect the
failure process of the pyramidal core. When the core plate thickness is 2mm, only one plastic hinge
appears in the compression process, and the core has strong compressive resistance. When the core
plate thickness is 1mm, the core starts to have two plastic hinges. As shown in Figure 5 (b), when the
press displacement is 0.2mm, the truss quickly loses stability, two plastic hinges appear at the same
time and the ability of pressure resistance continues to decrease. In addition, double plastic hinge also
delayed the contact between the panel and the core. The load-displacement curve of different core
plate thickness is shown in Figure 6. As can be seen from Figure 6, the core plate thickness has a
significant effect on the ability of pressure resistance. By increasing the core plate thickness the
deformation resistance performance of the pyramid increases and the modulus of the flat
compression increases significantly. According to the formulas (5) and (6), the equivalent flat
compressive strength and modulus with different core plate thickness are shown in Table 2. With the
increase of core plate thickness, the equivalent flat compressive strength and the equivalent flat
Simulation of Compression Properties of Pyramidal Sandwich Panels of TC4 Titanium Alloy
111

compressive modulus increase accordingly. In addition when the core plate thickness increases, the
relative density increases correspondingly.
Table 2. Equivalent flat compressive strength and modulus under different core plate
thickness.
Core plate thickness (mm) 0.6 1 1.5 2
Relative densit
y
(%) 0.84 1.40 2.10 2.80
Equivalent flat compressive strength (MPa) 1.13 2.71 5.97 7.93
Equivalent flat compressive modulus (MPa) 138.32 185.69 299.58 339.90
Strength-to-density ratio(MPa) 1.35 1.94 2.84 2.83
Modulus-to-density ratio(MPa) 164.67 132.64 142.66 121.39
2.3.3. Influence of the rid width. The panel thickness, core plate thickness and the unit size were set
to 1mm, 2mm, and 20mm. The width of ribs was set to 2 mm, 4 mm, 6mm, and 8mm respectively.
The simulation results show that the failure process is still a classic four-stage form similar to Figure
3: linear strengthening, buckling instability, contact strengthening and densification. It is worth
noting that the compression process with different ribs widths all has only one plastic hinge, this
means that the ribs width is not a key factor affecting the number of plastic hinges. The load-
displacement curve is shown in Figure 7. The equivalent flat compressive strength and modulus are
shown in Table 3. It can be seen that increasing the ribs width can significantly improve the pressure
resistance performance of the pyramid structure, and the relative density is also increasing to some
extent.
Table 3. Comparison of equivalent flat compressive strength and modulus under different
ribs width.
Ribs width (mm) 2 4 6 8
Relative density (%) 1.49 2.80 3.96 4.96
Equivalent flat compressive strength (MPa) 2.51 7.93 13.5 18.91
Equivalent flat compressive modulus (MPa) 107.48 339.9 643.18 1044.4
Strength-to-density ratio(MPa) 1.68 2.83 3.41 3.81
Modulus-to-density ratio(MPa) 72.13 121.39 162.42 210.56
Figure 7. Simulation of load-displacement curves with different ribs width.
IWMCE 2018 - International Workshop on Materials, Chemistry and Engineering
112

2.3.4. Influence of unit size. The thickness of panel, the core plate thickness and the ribs width were
set to 1 mm, 2 mm and 4 mm respectively to study the effect of unit size. The unit sizes were set as
15mm, 20mm, 25mm, and 30mm, respectively. The failure process went through linear strengthening,
buckling instability, secondary strengthening, and densification.
Table 4. Comparison of equivalent flat compressive strength and modulus under different unit
sizes.
Unit size(mm) 15 20 25 30
Relative densit
y
(%) 3.61 2.80 2.29 1.93
Equivalent flat compressive strength (MPa) 16.51 7.93 4.07 2.24
Equivalent flat compressive modulus (MPa) 1042.95 339.9 207.34 51.01
Strength-to-density ratio(MPa) 4.57 2.83 1.78 1.16
Modulus-to-density ratio(MPa) 288.91 121.39 90.54 26.43
Figure 8. Simulation of load-displacement curve under different unit sizes.
The load-displacement curves are compared as shown in Figure 8 and the equivalent flat
compressive strength and modulus are shown in Table 4. It can be seen that the smaller the unit is,
the greater the relative density is and the better the compressive performance is. It can be seen that
with the decrease of unit size, the compressive strength and the equivalent flat compressive modulus
increases, meanwhile, the relative density also increases, in addition, the equivalent flat compressive
modulus increase faster than the strength, which means that the unit size have much more influence
on the modulus
3. Conclusions
In this paper, finite element simulations of compression Properties of Pyramidal Sandwich Panels of
TC4 Titanium Alloy were carried out. The influences of panel thickness, core plate thickness, ribs
width, and unit size on the pyramidal sandwich compression properties were obtained. The
conclusions are as follows:
The panel is a major part of the weight of the structure but it has little influence on the pressure
resistance. The core is the main supporting part of the structure, increasing core plate thickness or
ribs width can increase the structure ability of pressure resistance. The smaller the unit is, the greater
the relative density and the higher stability of the structure are.
Simulation of Compression Properties of Pyramidal Sandwich Panels of TC4 Titanium Alloy
113

References
[1] Kooistra G W, Deshpande V S and Wadley H N G 2004 Compressive behavior of age
hardenable tetrahedral lattice truss structures made from aluminium J. Acta Materialia
52(14) 4229-4237
[2] Queheillalt D T and Wadley H N G 2009 Titanium alloy lattice truss structures J. Materials &
Design 30(6) 1966-1975
[3] Xue Z Y and Hutchinson J W 2004 A comparative study of impulse-resistant metal sandwich
plates J. International Journal of Impact Engineering 30(10) 1283-1305
[4] Yungwirth C J, Radford D D, Aronson M and et al 2008 Experiment assessment of the
ballistic response of composite pyramidal lattice truss structures J. Composites Part B
Engineering 39(3) 556-569
[5] Bele E, Bouwhuis B A and Hibbard G D 2012 Finite Element Analyses of Failure Mechanisms
and Structure-Property Relationships in Microtruss Materials J.
[6] Bouwhuis B A 2010 Microstructural strengthening mechanisms in micro-truss periodic
cellular metals J. Doctoral
[7] Lou J, Ma L and Wu L Z 2012 Free vibration analysis of simply supported sandwich beams
with lattice truss core Materials Science and Engineering: B. Nov20 177(19) 1712-6
[8] Li M, Li F M and Jing X J 2017 Active vibration control of composite pyramidal lattice truss
core sandwich plates Journal of Aerospace Engineering Dec 9 31(2) 04017097
IWMCE 2018 - International Workshop on Materials, Chemistry and Engineering
114
