
Study on Vacancy Defect Concentration and Hybrid
Potential of Metal-based Epitaxial Graphene with
Temperature
J H Gao, W Liu
*
, X X Ren and R L Zheng
Engineering Research Center of New Energy Storage Devices and Applications,
Chongqing Chongqing University of Arts and Sciences, Chongqing 402160, P.
R.China
Corresponding author and e-mail: W Liu, liuwei127@126.com
Abstract. This paper investigates the variation of the vacancy defect concentration and
hybrid potential of copper and nickel - based epitaxial graphene with temperature by
considering the existence of vacancy defects. Moreover, we discuss the impact of atomic non-
harmonic vibration on the metal - based epitaxial graphene. First, the concentration of
vacancy defects increases nonlinearly with increasing temperature, and the changing rate of
the vacancy defect concentration of the metal-based epitaxial graphene with temperature is
smaller than that of graphene; Second, the hybrid potential increases with increasing
temperature, but not much; Third, the hybrid potential is independent of temperature without
considering the atomic non-harmonic vibration which has an important influence on the
vacancy defect concentration and the hybrid potential. The higher the temperature is, the
more significant the non-harmonic effects are.
1. Introduction
Epitaxial graphene has attracted the attention of researchers worldwide for its application prospect
[1-4]. Conductivity is one of the most widely used and most important properties. Beside the
experimental research, many literatures have studied the conductivity of epitaxial graphene. In 2013,
Z Z Alisultanov studied the electrical conductivity of electron gas on metal-based and
semiconductor-based epitaxial graphene in Ref. [5]. In 2015, the variation of electrical conductivity
with temperature and thickness of little layer graphene and graphene nanosheets were studied,
indicating that the electrical conductivity gradually decreased with increasing temperature in Ref. [6].
However, these studies did not consider the existence of defects such as vacancies. In 2015, Davydov
made some discussions about the effect of epitaxial graphene vacancy defects on the density of
graphene in Ref. [7], nevertheless, neither the state density of epitaxial graphene on the specific
substrate, nor the relationship between the vacancy defect concentration and the temperature are
studied. At the same time, the physical model is established without taking the non-harmonic
vibration of the atom into account. Therefore, the hybrid potential of graphene is used as a constant
which is irrelevant to the temperature, and the experimental results of the electrical conductivity of
the epitaxial graphene with temperature cannot be explained well. Because of the preparation
194
Gao, J., Liu, W., Ren, X. and Zheng, R.
Study on Vacancy Defect Concentration and Hybrid Potential of Metal-based Epitaxial Graphene with Temperature.
In Proceedings of the International Workshop on Materials, Chemistry and Engineering (IWMCE 2018), pages 194-201
ISBN: 978-989-758-346-9
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

conditions and the thermal fluctuations of atoms, there are many defects in the epitaxial graphene,
such as vacancies, and the atoms are bound to undergo non-harmonic vibration at the equilibrium
position due to the thermal motion of microscopic particles. It is important to theoretically study the
properties of epitaxial graphene, such as density of state and conductivity, and investigate the
temperature dependent variation of vacancy defects and hybrid potential of epitaxial graphene.
However, the reports about the analytical formula with temperature changing have not yet been seen
so far.
Therefore, in this paper, by using the solid state physics theory and methods, the variation of the
hybrid potential and concentration of vacancy defects in epitaxial graphene with temperature as well
as the effects of non-harmonic vibrations on the variation are studied and compared with graphene.
This study has theoretical significance for revealing the properties of electronic energy states of
materials, and is important for improving material properties and preparing high-performance
electronic materials in practical applications.
2. Physical model and harmonic coefficients and non-harmonic coefficients
The system we studied consists of a single layer of grapheme, which has a hexagonal structure by
adsorbing N carbon atoms on a planar substrate of metal or semiconductor. The area is
LL
,its top
and side views are shown in Figure 1. Take any plane of carbon atoms as the origin of coordinates,
the monolayer graphene plane is the OXY plane, and the Z-axis vertical up to the graphene plane.
Base
Graphene
Figure 1. Top view and side view of epitaxial grapheme.
It is supposed that the ions in the metal substrate are stationary and the electrons are in motion.
Graphene has N carbon atoms, there are n
0
atoms from the normal position to form vacancies due to
the thermal excitation, the vacancy defect concentration is
Nn
0
. Since the graphene carbon
atoms interacting with each other, S.Yu.Davydov [8] gives the interaction between carbon atoms in
graphene
)(d
])(5
9
1[)(
2
2
1
2
12
2
2
V
V
dV
R
Vd
(1)
Where V
2
is the covalent energy of the sp
2
-bond σ bond between two atoms,which is inversely
proportional to the square of the bond length (distance between atoms) d:
222
2
26.3 dBmdV
,
where m is the mass of free electrons; V
1
is the metallization energy,
10
0
24
)2(10154.0 amR
, a0 is
the Bohr radius,
32
2
, which is a two-dimensional structure constant.
Due to the thermal motion, the graphene atoms perform non-harmonic vibration in the plane.
)(d
is expand near the equilibrium position of
0
d
and the deviation
0
dd
is very small, there is
4
2
3
1
2
00
2
1
)()(
d
(2)
Study on Vacancy Defect Concentration and Hybrid Potential of Metal-based Epitaxial Graphene with Temperature
195

where
])(
3
1
1[
3
20
2
2
1
4
0
2
2
V
V
d
V
are the harmonic coefficients, the first and second non-harmonic
coefficients of graphene carbon atom vibration. According to equation (1):
])(
3
10
1[
4
2
2
1
2
2
0
0
V
V
V
d
,
])(
3
5
1[
3
16
2
2
1
3
0
2
1
V
V
d
V
,
])(
3
1
1[
3
20
2
2
1
4
0
2
2
V
V
d
V
(3)
3. Variations of vacancy defect concentration in epitaxial graphene with temperature
Due to the thermal movement, the carbon atoms of graphene leave the original position to form
vacancy defects. If the metal-based epitaxial graphene is to form a vacancy defect, it is necessary to
overcome the effect of the metal atoms of the base (set the required energy to be
2
u
) and overcome
the effect of other carbon atoms (set the required energy to be
1
u
). Therefore, the energy
u
required
to form a vacancy defect can be considered as the sum of the two, that is,
21
uuu
, the
experimental value
eVu 5.00.7
1
[9] for the formation of a vacancy defect in graphene has been
given, and
2
u
can be considered as equal to the bonding energy W of the graphene carbon atoms to
the metal atoms of the base, that is,
Wu
2
. the change in the density of states of the graphene
system due to adsorption, the analytical formula W obtained is [10]:
im
WWW
(4)
where
m
W
and
i
W
are the metal components and ionization components of the adsorption energy.
)}
2
2
ln
4
1(]
)23)(2(3
24
222
2
[ln{)3ln21(
2
a
aa
aa
a
aa
aa
mmam
VW
a
eZ
W
i
44
1
22
0
(5)
Where
2
is called the half-width of the “pseudogap”[11],
eV
76.4
;
ae
ga
4)41(
2
0
,which is the atomic energy level,
g
is the work function of graphene
carbon atom,
eV
g
11.5
[11], a is the length of the adsorption bond, which is approximately equal
to the sum of the radius r
a
of the adsorption atom and the radius r
c
of the carbon atom, that is,
Ca
rra
; Z is the charge that the adsorbed atom had before it is adsorbed,
)3ln21(4
m
; V
m
is the interaction energy of the graphene s orbital with the
bond of the adatom atom p orbital, for
graphene-transition metal,
27223
)(
Caaspm
rrmrV
, the coefficient
95.2
sp
,
0
is the
vacuum dielectric constant.
Graphene forms n vacancy defects, causing the system entropy to increase, the increased amount
is
]!!)!(ln[ nNnNkS
B
, which causes the free energy of the system to change from F
0
to
STnwFF
0
. When the system reaches equilibrium, the free energy is minimal, considering
that both N and n are large and N >> n, the relationship between vacancy defect concentration α=n/N
and temperature T is obtained as following:
)exp(
Tk
w
B
(6)
IWMCE 2018 - International Workshop on Materials, Chemistry and Engineering
196

4. Variation of epitaxial graphene hybrid potential with temperature
According to the theory of solid physics[12], the hybrid potential is the average interaction energy of
electrons in the hybrid orbital, and it is proportional to the size of the overlapping region of the two-
atom hybrid orbitals. The largest direction of the electron cloud of the carbon four-hybrid orbit points
to the four corners of the tetrahedron (see Figure 2 a).
Supposed that the electron cloud of a hybrid orbital of carbon atom points to the positive x
direction and the maximum direction of a hybrid orbital electron cloud of carbon atom B to the
negative x direction, the hybrid orbits of the two atoms almost completely coincide in the direction at
equilibrium (see Figure 2 (b)). According to Ref. [4], the hybrid potential
22
mdV
, where
is the undetermined parameter which can be obtained from the hybrid potential of graphene given in
the literature. In equilibrium, the distance between atoms A and B is
0
d
. Because of the non-
harmonic vibration of atoms, the distance between atoms at any temperature is
]1[)(
0
TdTd
l
,
where
l
is the linear expansion coefficient at temperature
T
. When the temperature is moderate, it
is determined by the following formula[13]:
]
)3(
9
3
3
[
1
2
2
2
0
2
21
2
2
0
1
0
Tk
Tk
Tk
k
d
B
B
B
B
l
(7)
(a) (b) (c)
Figure 2. Variation of electron clouds caused by non-harmonic vibration.The hybrid orbital
distribution of Carbon
3
sp
hybrid orbital distribution (a), direction equilibrium (b) and vibrational
(c).
Due to the change in the distance between atoms, the overlap region of the electron clouds in the
x-direction hybrid orbitals of the two atoms changes (see Figure 2(c)), causing a change in the
hybridization potential. Since the hybridization potential is inversely proportional to the square of the
atomic distance, the hybrid potential at any temperature is:
2
0
22
0
2
)1(]1([
)(
T
V
Tmd
TV
ll
(8)
From equations (7) and (8), we can see that the non-harmonic vibration of atoms has an important
influence on the hybridization potential.
Study on Vacancy Defect Concentration and Hybrid Potential of Metal-based Epitaxial Graphene with Temperature
197

5. Effect of atomic non-harmonic vibration on the variation of vacancy defect concentration
and hybrid potential with temperature
The lattice constants
ma
Cu
10-
1061.3
and
ma
Ni
10-
1061.3
of copper and nickel are given in Ref.
[14], and the atomic radii
mr
Cu
10
1027.1
and
mr
Ni
10
102445.1
and the radius of carbon
mr
C
10
1077.0
are obtained from the crystal structure. The interaction energy
m
V
between
graphene and the substrate is obtained. Substituting the data of
eV
76.4
and
eV
g
11.5
given in Ref. [11] into formula (5), we can get
m
W
,
i
W
and
im
WWu
2
for copper and nickel
substrates, respectively. Then, the experimental value
eVu 5.00.7
1
of graphene forming a
vacancy defect is given by Ref. [9], and the energy
u
required to form a vacancy defect is obtained.
For copper base
eVu
Cu
6526.9
; for nickel base
eVu
Ni
6768.9
. Substituting it with
123
.1038.1
KJk
B
into equation (6), the variation curve of vacancy defect concentration
versus temperature for copper and nickel-based epitaxial graphene is obtained, as shown in Figure
3(b) and Figure 3(c) and Table 1. For comparison, Table 1 and Figure 3(a) also show the change of
the concentration
of vacancy defect in graphene with temperature.
Table 1. Variation of vacancy defect concentration of graphene, copper - based and nickel - based
epitaxial graphene with temperature.
T/K
700
800
900
1000
1100
1200
1300
Graphene(×10
-28
)
0
0
0
0
0
0.004
7.706
Copper-base(×10
-38
)
0
0
0
0
0
0.003
4.120
Nickel-base(×10
-38
)
0
0
0
0
0
0.002
3.302
As can be seen from Table 1 and Figure 3, first, the concentration of vacancy defects increases
with temperature nonlinearly for both graphene and epitaxial graphene. At T<1200 K,
the
concentration of vacancy defects almost reaches 0. However, when the temperature is higher than
1200 K, the vacancy defect concentration sharply increases with increasing temperature. Second, At
the same temperature, the concentration of vacancies in graphene is much greater than that in
epitaxial graphene, and its variation with temperature is much greater. In other words, the graphene is
more likely to form vacancy defects and is more readily be affected by temperature.
The equilibrium bond length of graphene carbon atom d
0
=1.42×10
-10
m, V
2
=12.32eV, V
1
=20.08m,
R=10.08eV.(10
-10
m)
12
are given by Ref. [15], and the simple harmonic coefficient and the first and
second non-harmonic coefficients of the graphene atom vibration are obtained from equation
(3):
22
0
.105388.3
mJ
,
312
1
.104973.3
mJ
,
422
2
.102014.3
mJ
. Ref. [5] also gives
the hybrid potential
eVV 0.2
0
of epitaxial graphene at zero temperature. From equations (7) and
(8), the hybrid potential of epitaxial graphene varies with temperature as shown in Figure 4, where
lines 0, 1 and line 2 are the results of simple harmonic approximation, only the first non-harmonic
term, and the first and second non-harmonic terms, respectively.
IWMCE 2018 - International Workshop on Materials, Chemistry and Engineering
198
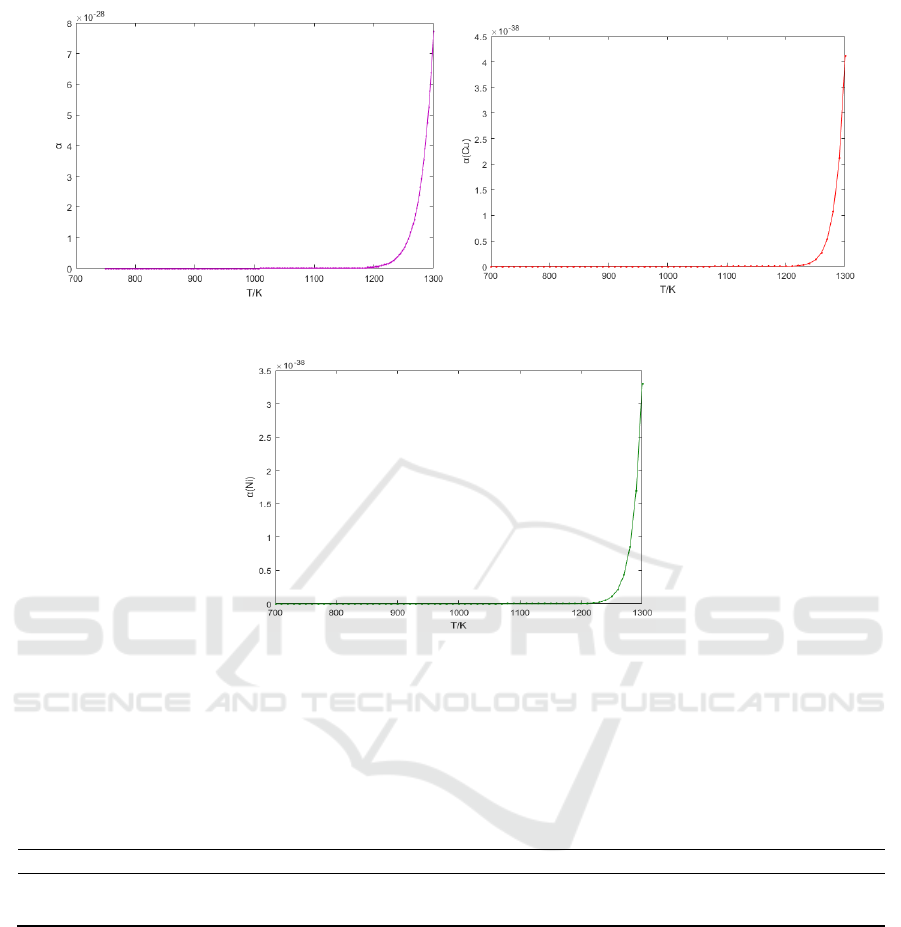
(a) (b)
(c)
Figure 3. Variation of vacancy defect concentration of graphene (a), copper - based (b) and nickel -
based epitaxial graphene (c) with temperature.
Table 2. Variation of Silicon (Si) Based Epitaxial Graphene Hybrid Potential with Temperature.
T(K)
300K
500K
700K
800K
1000K
1100K
1300K
V1(ev)
2.009811
2.016391
2.023003
2.026321
2.032982
2.036324
2.043032
V1,2(ev)
2.009811
2.016391
2.023005
2.026323
2.032986
2.036329
2.043040
Study on Vacancy Defect Concentration and Hybrid Potential of Metal-based Epitaxial Graphene with Temperature
199
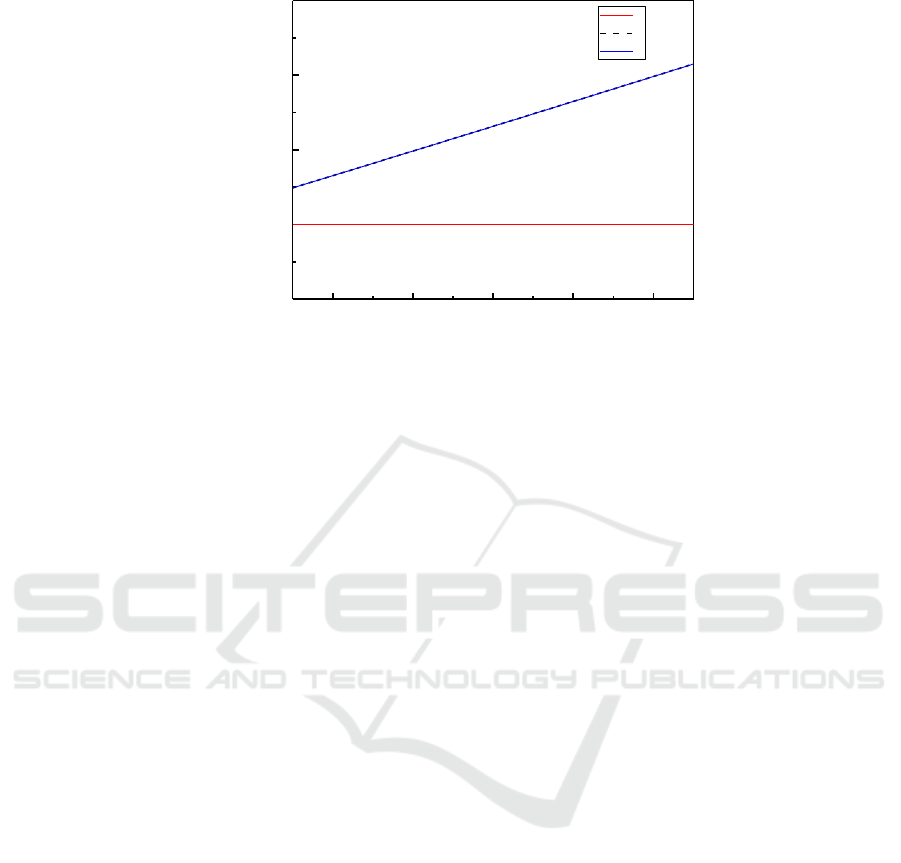
400 600 800 1000 1200
1.98
2.00
2.02
2.04
2.06
2
1
V (eV)
T /K
0
1
2
0
Figure 4. Variation of Silicon (Si) Based Epitaxial Graphene Hybrid Potential with Temperature.
It can be seen from Table 2 and Figure 4 that in the case of harmonic approximation, the hybrid
potential of epitaxial graphene does not change with temperature. However, if taking into account the
non-harmonic vibration of the atoms, the hybrid potential increases with the increase of temperature,
but the change is not significant. When the temperature rises, the hybrid potential increases by only
1.65%. Also, it is noticed that the higher the temperature is, the greater the difference between the
values of the non-harmonic and harmonic approximations is, that is, the non-harmonic effects
become more significant.
6. Conclusions
In summary, the variation of the concentration and the hybrid potential of metal-based epitaxial
graphene with temperature are studied. First, the concentration of vacancy defects in both graphene
and metal-based epitaxial graphene increases nonlinearly with increasing temperature. The vacancy
defect concentration of epitaxial graphene and its change rate with temperature are more significant
than that of graphene. Second, the hybrid potential increases with the increase of temperature, but the
change is not great. Third, the atomic non-harmonic vibration has an important influence on the
variation of the hybrid potential with temperature. The higher the temperature is, the more significant
the change is, and the more significant the non-harmonic effect is.
References
[1] Castro A H, Guinea F, Peres N M R, Novoselov K S, Geinm A K 2008 Rev. Mod. Phys. 81
109
[2] Haas J, De Heer W A, and Conrad E H 2008 J. Phys. C: Condens. Matter 20 323202
[3] Wu Y H, Yu T, Shen Z X 2010 J. Appl. Phys. T108 071301
[4] Das Sarma S, Adam S, Hwang E H, Rossi E 2011 Rev. Mod. Phys. 83 40
[5] Alisultanov Z Z 2013 Tachnical Physics Letter 39 17 8-16
[6] Fang X Y, Yu X X, Zheng H M, Hai B J and et al 2015 Physics Letters A 379 37 2245-2251
[7] Davydov S Y 2015 Semiconductors 49(8) 1095-1103
[8] Davydov S Y 2014 Physics of the Solid State 56(4) 849-853
[9] Thrower P A,Wayer R M 1978 Point defects and self-diffusion in graphite Phys. Stat. Sol.(a).
47 11-37
[10] Davydov S Y 2011 Adsorption atoms and bond energy of monolayer graphene Physics of the
Solid State 53 12 2412-2423
IWMCE 2018 - International Workshop on Materials, Chemistry and Engineering
200

[11] Davydov S Y and Subinovu G I 2011 Physics of the Solid State 53 3 608-616
[12] Huang K and Han R Q 2013 Solid state physics (Beijing: Higher Education Press ) 552-555
[13] Cheng Z F and Zheng R L 2016 Acta Phys. Sin. 65 104701
[14] Kittle C (translated by Yang S H) 1979 Introduction to Solid State Physics (Beijing: Science
Press) 45
[15] Davydov S Y 2011 Technical Physics Letters 37 42
Study on Vacancy Defect Concentration and Hybrid Potential of Metal-based Epitaxial Graphene with Temperature
201
