Elliptical Gear Dynamic Analysis Based on ANSYS Workbench

Jian Zhang

，Peng Rao

，Bin Zheng

and Xuemei Qi

1School of Transportation and Automobile Engineering, Panzhihua University, China

Keywords: Elliptical gear; parametric modelling; dynamics; Pro/E; ANSYS.

Abstract: Aiming at the problem of 3D parametric modeling and dynamic analysis of elliptical gears, an elliptical gear

was taken as the object of study, and the three - dimensional parametric modeling of elliptical gear was

realized by combining MATLAB parametric design and Pro/E entity. Through the modal, harmonic

response and transient dynamics analysis of the elliptical gear by using ANSYS, the first six natural

frequencies of the elliptical gears and the distribution modes of the main modes and corresponding

displacement response curves, strain cloud maps and stress response curves were obtained. The results of

dynamic analysis show that the elliptical gear stress and deformation are more serious suffered in the

direction of long diameter, keyway direction and keyway, so it should be considered in the design and

optimization of elliptical gear.

1 INTRODUCTION

Elliptic-gear pitch curve is irregular, therefore it is

quite difficult to determine each-tooth direction and

position, which greatly increases the difficulty of

modeling 3D and reduces the efficiency and

precision [1]. Study on kinematics characteristics of

mechanical movement parts gets vibration

characteristic through modal analysis to provide

fundamental analysis data for harmonic response,

transient dynamics, which judges the rationality of

gear pair design and weak position, provides

reference for optimal design, for example, elliptical

gears pair[2-3]. With unique non-linear dynamic

characteristics, elliptical-gears dynamic analysis is

more complex compared to circular gears [4-8].

In order to improve the modeling accuracy and

efficiency of elliptical gears, parameterized hybrid

modeling of MATLAB and Pro/E was used. Modal,

harmonic response and transient dynamics analysis

were analyzed by using ANSYS Workbench. Then

the dynamics parameters distribution regularities

were obtained, and found out the elliptic gear stress

concentration and easily damaged parts to provide

reference for elliptical gear and other non-circular

gear design and optimization.

2 ELLIPTIC GEAR MODELING

Table 1: The elliptic gear basic parameters.

Gear parameters Value

Order n

Eccentricity e

0.6

Number of teeth Z

Breadth tooth b(mm) 14

Addendum coefficient 1

Root clearance coefficient c 0.25

Modulus m(mm) 3

Angle of pressure α(°) 20

Elliptic gear design flow chart is shown in Fig 1.

According to the Fig1, 2 order elliptical solid

model is established by using MATLAB and Pro/E,

as shown in Fig 2, and its basic parameters are

shown in Table 1.

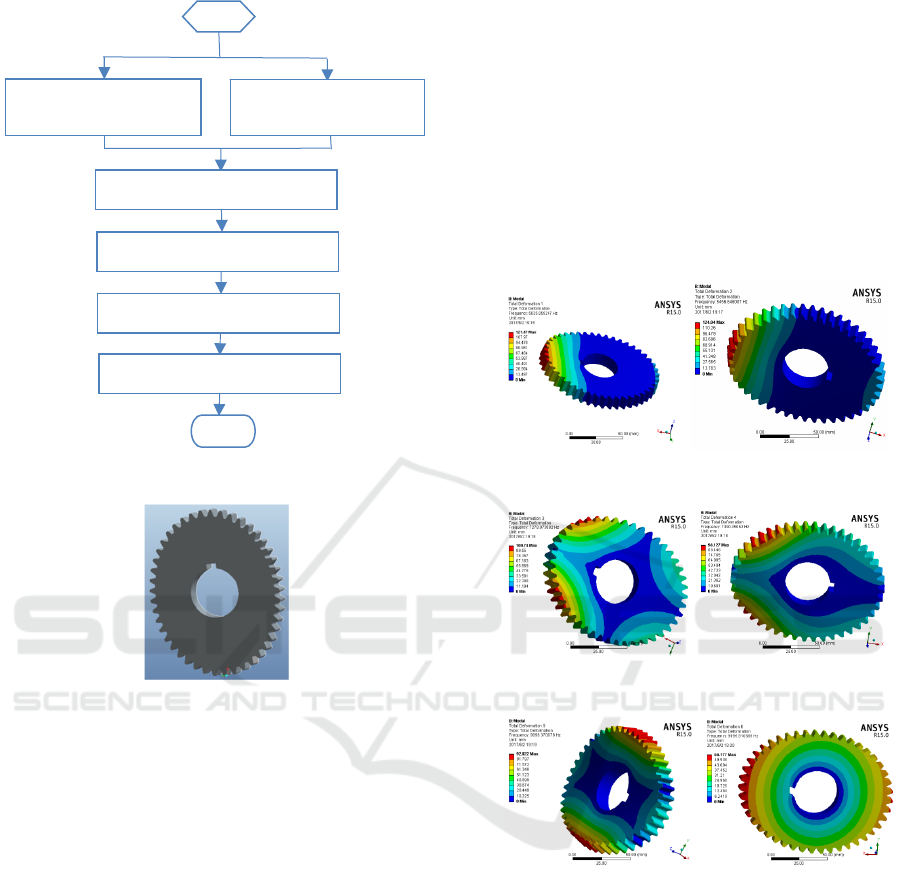
Figure 1: Elliptic gear design flow chart.

Figure 2: Elliptic gear model

3 MODAL ANALYSIS

3.1 Modal Analysis Theory

Modal analysis, that is, free vibration analysis and a

modern method for studying the structures dynamic

characteristics, which can be used to determine

natural frequencies, vibration mode and vibration

mode participation coefficient, which is how much

extents some vibration mode participates in

vibrating in a certain direction.

For modal analysis, the analytical formula is:

[] []

()

{}

MK φω

(1)

In formula (1), φi is modal; ωi is vibration

frequency ； K is stiffness matrices; M is mass

matrix.

Elliptical-gear natural frequency and each order

vibration mode are infinite, while each natural

frequency and corresponding main vibration modes

represent the free vibration modal of a single

freedom system. This modal is non-circular gear

basic vibration characteristics which plays a decisive

role in low order mode. Therefore, it is only

necessary to analyze the modal vibration of elliptical

gears under low order natural frequencies when we

perform modal analysis.

3.2 Modal Result Analysis and

Evaluation

(a) One order mode (b) Two order mode

(e) Five order mode (f) Six order mode

Figure 3: Modal vibration modes

The material of the two order elliptical gear is 45

steel, the mesh cell size is 10mm, torque is 105 N•m,

the phase angle is 0. Through modal analysis for

inner hole constrain conditions, six vibration modes

and their natural frequencies are shown as Fig 3.

Below the graphics window of “Mechanical” ，

natural frequencies of the models can be obtained, as

shown in Table2.

Define curve function

ased o

Elliptic geometry

The principle of cutting

tool

Tooth profile function

Draw profile figure by using MATLAB

Pro/E entity manipulation

3D model

End

Start

Table 2: Elliptical-gear natural frequency.

Mode Frequency [Hz]

1 5035.1

2 5456.6

3 7280

4 7390.1

5 9096.4

6 9195.8

According to Figure 3 and Table II, elliptical-

gear one order frequency is 5035.1Hz. The main

deformation is that X-axis positive direction teeth

tension and bend along the Z axis. The two order

frequency is 5456.6 Hz, the main deformation and

one order deformation are axisymmetric about the Z

axis. The three order frequency is 7280Hz, the main

deformation is left and right teeth X-axis positive

direction stretch and bending along respectively Z-

axis positive and negative direction ； The four

frequency is 7390.1 Hz，the main deformation is

that left and right teeth of X-axis negative direction

stretch and bending respectively along Z-axis

positive and negative direction; The five frequency

is 9096.4Hz ， the main deformation is Y-axis

direction teeth symmetrically stretched and bending

along Z axis；The six frequency is 9195.8 Hz， the

main deformation is that the teeth in the long half

axle stretch along the angle between the X axis and

the Y axis. The reason is that the vibration frequency

generated by external excitation is close to elliptical-

gear natural frequency, initiating resonance.

Therefore ， we should manage to avoid this

frequency range during design to improve gear life

span.

4 HARMONIC RESPONSE

ANALYSIS

4.1 Harmonic Response Analysis Theory

Harmonic response analysis is a technique used to

determine the steady-state response of linear

structures bearing load varying with time in

accordance with the sinusoidal (harmonic) rule. The

purpose of the analysis is to calculate response of

structure at several frequencies and obtain some

response values (usually displacements)

corresponding frequency curves.

The equation of motion of harmonic response is

：

[] [] []

()

{} {}(){}{}()

2121

FiFiKCiM

+=+++

φφωω

(2)

Setting up the stiffness matrices[K] and mass

matrix [M] are constant values, and the material is

linear, using small displacement theory (not

including non-linearity), damping is[C], and

harmonic loading is[F].

Harmonic response analysis aims to calculating

the response at the excitation frequency and

obtaining the frequency response curves. Gear

“peak” response can be found through the curve.

4.2 Harmonic Response Analysis and

Evaluation

The material of the two order elliptical gear is 45

steel, the mesh cell size is 10mm, torque is 105 N•m,

the phase angle is 0. The harmonic-response analysis

for gear inner hole conditions, we get the gear unit

of each order response angle and deformation，gear

unit each order frequency and phase angle，the gear

node change curve with frequency and displacement

response cloud map are shown as Fig 4.

(a) Each order response angle of gear unit

（b）Each order deformation curve gear unit

（c）Response frequency curve of gear unit

（d）Gear node change curves with frequency

（e）Displacement response cloud chart

Figure 4: Harmonic response analysis result

According to （a），（b）, the elliptical gear

unit each order response angles and deformations

follow harmonic response equation, whose period，

input and output are same. According to（c），

with the increase of input frequency, each order

response frequency also increase, the phase angle

remains 180°, but it changes suddenly and sharply

reduced to zero near to the final value. According to

（d ），gear node response frequency curve and

phase angle change with frequency, and unit each

order response frequency and phase angle change

with frequency are the same. According to （e），

gear long axis direction displacement is larger,

especially the keyway direction. We can infer that,

in actual movement, elliptical-gear stress mainly

concentrates on keyway direction and the part where

the radius of curvature is longer. Thus, this part is

more vulnerable to damage. This part should

strengthen when processing.

5 TRANSIENT DYNAMIC

ANALYSIS

5.1 Transient Dynamic Analysis Theory

Transient dynamic analysis (also called time history

analysis) can be used to determine the dynamic

response while structures are subjected to arbitrarily

varying loads. Non-circular gears transient dynamics

can determine gear’s displacement, strain, stress and

force vary with time under the random combination

action of steady state load, transient load and

harmonic load.

The basic motion equation of transient dynamics

is：

)(

tFKuuCuM

=++

&&&

（2）

In formula (3) ， M is mass matrix ； C is

damping matrix ； K is stiffness matrices ； is

Nodal acceleration vector ； is Nodal velocity

vector；u is Node displacement vector.

In order to analyze whether two order elliptical

gear can bear low speed impact, some questions

such as vibration response caused by gear over

convex point need to do transient dynamics analysis.

5.2 Analysis and Evaluation of Transient

Dynamics Results

The material of the two order elliptical gear is 45

steel, and the mesh cell size is 10mm, torque is 105

N •m, the phase angle is 0. The harmonic-response

analysis for gear inner hole condition ， we get

elliptical gear displacement and stress changes are

shown in Fig5.

（a）Deformation analysis cloud map

（b）Displacement response curve

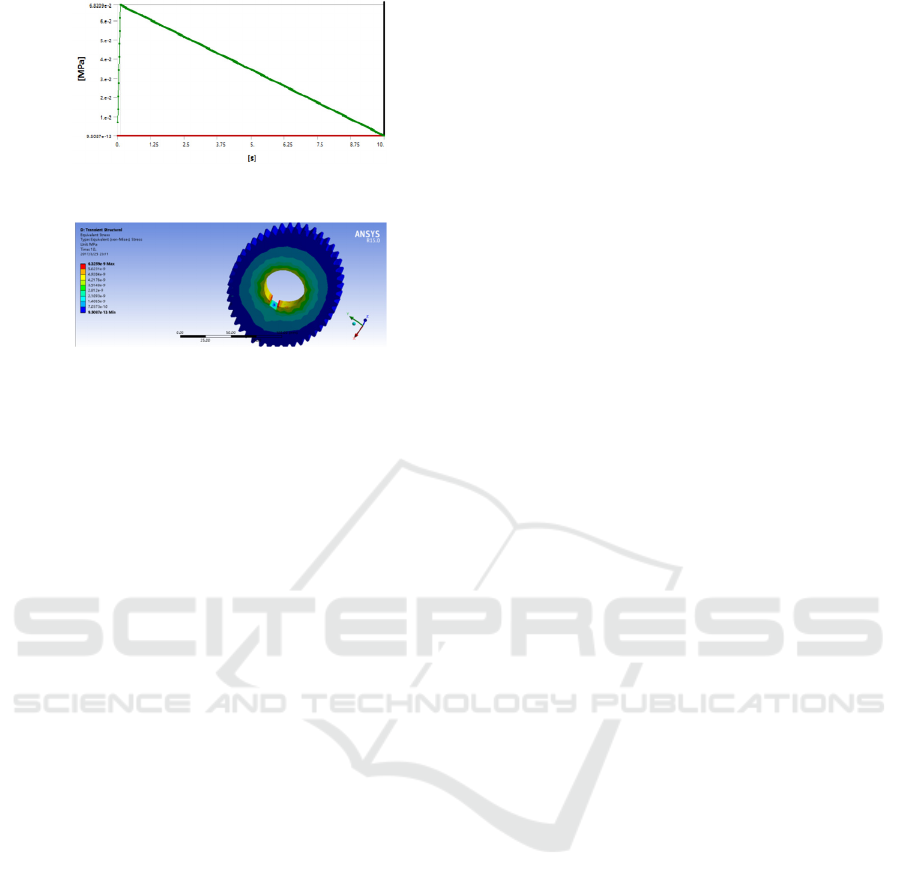
（c）Stress response curve

（d）Stress cloud map

Figure 5: Transient dynamic analysis result

According to （ a ），the gear long axis

deformation is bigger, especially the keyway

direction. We can infer that, in actual movement,

elliptical gear longer-pitch-diameter parts and

keyway direction are much more vulnerable to

damage. According to 5（b）and（c）, elliptical

gear displacement and stress change synchronously

with time, the mutation at the starting point increases

sharply, and decreases with the passage of time.

According to（d）, in actual movement, gear bore

diameter and shaft outer diameter interference fit

through. Bore diameter bear torque delivered by

shaft and produce stress. Because of the stress

concentration produced by the keyway, there is more

vulnerable to damage.

6 CONCLUSIONS

First, through modal analysis the first six nature

frequencies and principal vibration mode are

obtained by using ANSYS Workbench. The

vibration frequency produced by external excitation

is close to the nature frequency, which is vulnerable

to cause resonance. So, we manage to avoid this

frequency range during then design. Second, through

harmonic response analysis, pitch response

frequency curve and displacement response cloud

maps are obtained whose results show that stress is

mainly concentrates on the long diameter and

keyway direction. Therefore, this part is vulnerable

to damage. Finally, through transient dynamics

analysis, deformation and strain cloud maps and

displacement and stress response curves are

obtained. Elliptical gear stress and deformation are

more serious suffered in the direction of long

diameter, keyway direction and keyway, so it should

be considered in the design and optimization of

elliptical gear.

ACKNOWLEDGMENT

This work was financially supported by the

Education Department of Sichuan province in 2016

scientific research program of natural science project

(16ZB0482) and the national innovation training

program for college students (201411360016).

REFERENCES

1. Chaozhao Yan, Zhudian Guan, Yang Chen. Design

System of the High Order Elliptic Gear Pair Pitch

Curve based on the SolidWorks[J]. Journal of

Mechanical Transmission, 2017, (01): 169-172.

2. Yuchun Zou, Fang Ren, Jianzhao Yang. Harmonic

response analysis for main shaft device of single rope

winding mine hoist based on ANSYS Workbench[J].

Coal Engineering,2017, (03): 100-102+106.

3. Pingyong Liu, Cun Yang, Xuan Sun. Kinematics

Simulation Analysis of Non-circular Gear based on

ADAMS[J]. Journal of Mechanica Transmission,

2014,06:106-109.

4. Honggao Yu, Pingjia Yu, Huajia Tong. Design of a

conjugate concave-convex Non-circular Gear

Mechanism[J]. China Mechanical Engineering,2016,

(16): 2155- 215+2165.

5. Jun Liu, Haitao Liu. Mode Analysis of a 3-DOF PKM

module[J]. Journal of Machine Design,2017,(04):17-

23.

6. Zhong Liu, Weizhan Gao, Minghuan Huo. Vibration

Mode Analysis of Valve Controlled Cylinder Type

Hydraulic Elevator[J]. Machine Tool &

Hydraulics,2017, (01):125-128.

7. Nantie Liu, Yansong Tian, Yusu Liang. The transient

dynamics analysis of monorail car rail unit[J]. Chinese

Journal of Engineering Design,2016, (04):352-35.

8. Lilin He, Li Hou, Li Bo. Dynamic Analysis of

Cylindrical Gear with Curvilinear Shape Teeth Based

on UG and ADAMS[J]. Modular Machine Tool &

Manufacturing Technique,2016, (04): 12-15.