Study on the Mechanical Behavior of the Dec

pavement by the

Whole Bridge – Local Box Girder - Orthotropic Plate Threestage

Method

Mingzhi Sun

, Xiong Tang

and Xiaohao Wei

Research Institute of Highway Ministryof Transport, Beijing 100088, China

School of transportation, Southeast University, Nanjing 211189, China

Keywords: Steel bridge; orthotropic plate; deck pavement; mechanical behavior; three-stage method.

Abstract: The mechanical analysis of the traditional orthotropic plate local model can not simulate the real

deformation state of the bridge deck pavement. Therefore, this paper adopts "the whole bridge - local girder

- orthotropic plate" three stage mechanics analysis method. The simulation analysis model of whole multi-

tower and multi-span bridge was established to obtain the dynamic response characteristics of whole bridge

and the boundary conditions of local box girder model. According to the calculation results of the local box

girder model, the most adverse area of dynamic response for deck pavement was found. The local

orthotropic plate composite model was established to calculate the most adverse stress, strain and

interlaminar shear stress of the deck pavement. The calculated results can be used as the main technical

indexes of bridge pavement materials and structural design.

1 INTRODUCTION

The large span steel bridge has developed rapidly in

recent decades. Due to the advantages of self-weight

and span., most of the steel bridge deck is adopted

orthotropic structure. The thin layer asphalt concrete

was generally used as paving layer on the large span

steel bridge. The pavement layer and the orthotropic

plate bear the external load together. Therefore, the

pavement layer and the orthotropic plate need to be

analyzed as a whole when analyzing the mechanical

deformation of the pavement layer(Qian, 2001and

2005). Due to the effect of steel plate stiffening rib,

there is obvious stress concentration in the contact

position between the paving layer and the stiffening

rib. The maximum stress and mechanical properties

of the pavement layer can not be calculated

accurately by using beam board theory. The most

effective analytical tool for solving this problem is

the finite element analysis method(Ai, 2017; Chen,

2016; Zhou, 2007).

But in past research, the boundary condition of

the model was often simplified, and the influence of

whole bridge characteristics was not

considered(Zhang, 2017; Yang, 2018). This paper

innovatively developed the three-stage analytical

method. The displacement value obtained by the

whole model in the previous stage is used as the

boundary condition of the local model in the latter

stage. This method can simulate the mechanical

response more accurately of the bridge deck

pavement, and the calculated results can be used as

the main technical indexes of bridge pavement

materials and structural design.

2 THE MECHANICAL

RESPONSE OF WHOLE

BRIDGE MODEL

2.1 Finite Model of Whole Bridge

The whole bridge model is set up based on finite

displacement theory. The main tower and pier are all

simulated by the space beam element. stiffening

girder was simulated by shell element. The bridge

deck pavement and railings are simulated by mass

unit which is only considered its mass and not

considered its rigidity.

2.1.1Simplifythe Components of Main

Bridge

When establishing the suspension bridge model, the

key is to simplify the bridge tower, main cable, sling

and bridge deck.

1) Main cable and derrick

In order to make the analysis method more

universal, space beam element was selected to

simulate the main cable.The derrick is the link

between the stiffening girder and the main cable

which is mainly pulled. The bar element was used to

simulate the derrick in this study. The connection

diagram of main cable and derrick is shown in

Figure 1.

Figure 1: The connection diagram of main cable and

derrick.

2) Stiffening girder

In addition to the bridge panel and floor, the steel

box girder of the bridge has a large number of

diaphragm plate and stiffening rib. The structure is

very complicated.If the finite element model is

generated directly by the actual structure, the

number of units is inestimable and the computation

workload is huge.

In the premise of ensuring the consistency of

dynamic and static parameters, the equivalent model

of composite box girder with different materials is

used to equivalent the original stiffening beam.The

vertical bending stiffness, transverse bending

stiffness, torsional stiffness, mass distribution and

mass inertialdistribution of the model are equivalent

to the entity.In this study, the orthogonal anisotropic

shell element is adopted to carry out the dispersion

of the suspension bridge stiffening beam.

3)Main tower

The finite element model of the main tower can

be directly generated on the main tower. However,

this model has too many grid， and it will cost too

much time in computation. In this study, the column

and horizontal beams are treated as beams, the cross-

section beam element has same cross section

characteristic, material and quality with the object.

2.1.2 Section Properties and Material

Parameters of Each Component

The section properties and material parameters of

each component for the whole bridge are shown as

Table 1.

Table 1: Section properties and material parameters of each component.

Com

onent A/m

E/Pa

(

)

Main girde

1.56 8.21 192 3.02 2.1×10

7850

Main cable 0.327 0 0 0 2.0×10

7850

Derric

0.005 0 0 0 2.0×10

7850

Main towe

1.556 7.26 7.2 5.59 2.1×10

7850

e towe

29.6 365 293 180 3.4×10

2600

In Table 1, A is sectional area; J

is torsional moment of inertia; I

is transverse bending moment of inertia; I

is vertical

bending moment of inertia; E is elastic modulus; ρ is density.

2.1.3 The Loading of Main Bridge

In this paper, the deck pavement deformation of the

orthotropic steel bridge under constant load and

automobile load is analyzed, and the related load is

as follows.

1)The constant load of stiffening girder

The first period of constant load: q

= 178.1kN/m

(standard section), q

= 213kN/m (special section,

36m on both sides of the main tower);

The second period of constant load: q

53.1kN/m.

2) Cable system

Main cable wire: 50.3kN/m; Wire: 0.96kN/m;

Main cable inspection walkway: 0.316kN/m; Cable

clamp and sling: 6.382kN/m (middle span), clamps

1.079kN/m (side span); Main cable surface coating:

0.012kN/m.

3) Vehicle load

According to the highway bridge general

specification, vehicle load is chosen as highway -I

level which is applied by influence line method.

2.1.4 Finite Element Model

The appropriate beam element and shell element

were selected to establish the whole bridge model.

The concrete model is shown in the Figure 2 and

Figure 3.

Figure 2:Simulation model of whole bridge.

Figure 3: Local model of the structure near the main tower.

2.2 The Mechanical Response Analysis

of the Whole Bridge

2.2.1Basic Dynamic Response

Characteristics

The modal analysis of the bridge is carried out to

study the difference between the three tower and two

span suspension bridge and the other two tower

suspension bridges. According to the results of the

whole bridge, the technical requirements of the deck

pavement system can be studied. The calculation

results of Taizhou bridge are compared with the two

tower suspension Bridges, such as Jiangyin Yangtze

river bridge, Runyang Yangtze bridge and other

bridges as shown in Table 2.

Table 2 The comparison of self-vibration characteristics between different suspension bridge.

Vibration mode Taizhou bridge

(2*1080m)

Runyang bridge

(1450m)

Jiangyin bridge

(1385m)

Single span

bridge

(1080m)

First order positive symmetrical vertical bending 0.1171 0.1241 0.1344 0.1496

First order negetive symmetrical side bending 0.0712 0.0884 0.0920 0.0852

First order positive symmetrical side

ending 0.1016 0.0489 0.0509 0.0704

First order negetive symmetrical side bending 0.0765 0.1229 0.1169 0.1153

First order negetive symmetrical torsion 0.2454 0.2698 0.2747 0.3203

Due to the bridge tower was effectively anchored

by the main cable of side span and greatly enhance

the structure stiffness, the frequency of each order

for the two tower bridges was significantly improved

in addition to first order positive symmetrical side

bending compared with three tower suspension

bridge. The anchorage effect for the main cable of

side span is very important to improve the structure

stiffness of the suspension bridge. The anchorage

effect of the middle tower for the three tower

suspension bridge is relatively weak. The vertical

deflection of the main girder under vehicle load

increase significantly relative to the two tower

suspension bridge, the torsion ability of main girder

decreases, the biggest torsion angle increases, and it

also produces new requirements for bridge deck

pavement system.

2.2.2 The Most Adverse Position of Deck

Pavement in the Whole Bridge

The stress of the main beam is mainly bending

moment. The force analysis can be equivalent to the

bending bar. The greater the bending moment of the

main beam is, the greater the relative deformation of

the adjacent units in the main beam and the deck

pavement under the active load is. The longitudinal

tensile stress of deck pavement will be more

evidently influenced by the mechanical

characteristics of the whole bridge. Therefore, the

vertical bending moment is used as the control index

to select the most adverse section of main beam.

Figure 4: Vertical bending moment envelope of the whole

bridge.

Table 3:The bending moment range of each control section for the whole bridge.

As shown in Figure 4 and Table 3, the maximum

vertical bending moment is 1.55*10

kN·m under

constant load and the most adverse vehicle load

located at the position which is 20m from the middle

tower. The minimum vertical bending moment is -

1.47*10

kN·m located at the location of the middle

tower. Therefore, the 64m box girder near middle

tower of the suspension bridge is selected as the

most adverse box girder with the maximum stress as

shown in Figure 5.

Figure 5: Diagram of the most adverse girder section.

3 THE MECHANICAL

RESPONSE OF LOCAL BOX

GIRDER

In order to reflect the local beam section of the

model under the mechanical characteristics of the

whole bridge environment, when establish the model

of local beam section, not only the boundary

condition should be extracted from the whole bridge,

but also the force condition must be consistent with

the corresponding beam segments in the whole

bridge model. The node displacement on both ends

of the beam section of box girder was extracted,

after linear interpolation the node displacement was

added as boundary conditions of local box girder

model.

Take the section of node 20926 and 7168 in

Fig.5 as an example, the external forces and the

displacement obtained by the whole bridge

simulation are loaded to the most adverse local box

girder section. The bending moment loading

diagram is shown in Figure 6.

Figure 6:The bending moment loading at the beam-end of

local box girder.

The purpose for the 3-d finite element

calculation of local box girder model is to determine

the stress concentration area of the bridge deck slab

under the action of vehicle load as shown in Figure

7. The boundary condition at the most adverse area

of the deck pavement was obtained which will be

used at the next stage calculation.

Figure 7: The force adverse area of the deck pavement.

4 THE MECHANICAL

RESPONSE OF LOCAL

ORTHOTROPIC PLATE

COMPOSITE MODEL

In order to obtain the mechanical response of the

most adverse deck pavement, local orthotropic plate

composite modelwas established by using the

boundary condition of the local box girder model

calculated in previous section. The load was applied

with the highway I-level, and the impact coefficient

was 1.3. The axial load in calculation was 140kN

and the tire pressure is 1.00MPa as the pavement

load standard.

Steel bridge deck is a kind of structural

orthotropic structure. During the calculation, the

steel bridge deck is assumed as uniform, continuous

and isotropic elastic material. The geometric

dimensions and material parameters of each

component in steel bridge deck are shown in Table

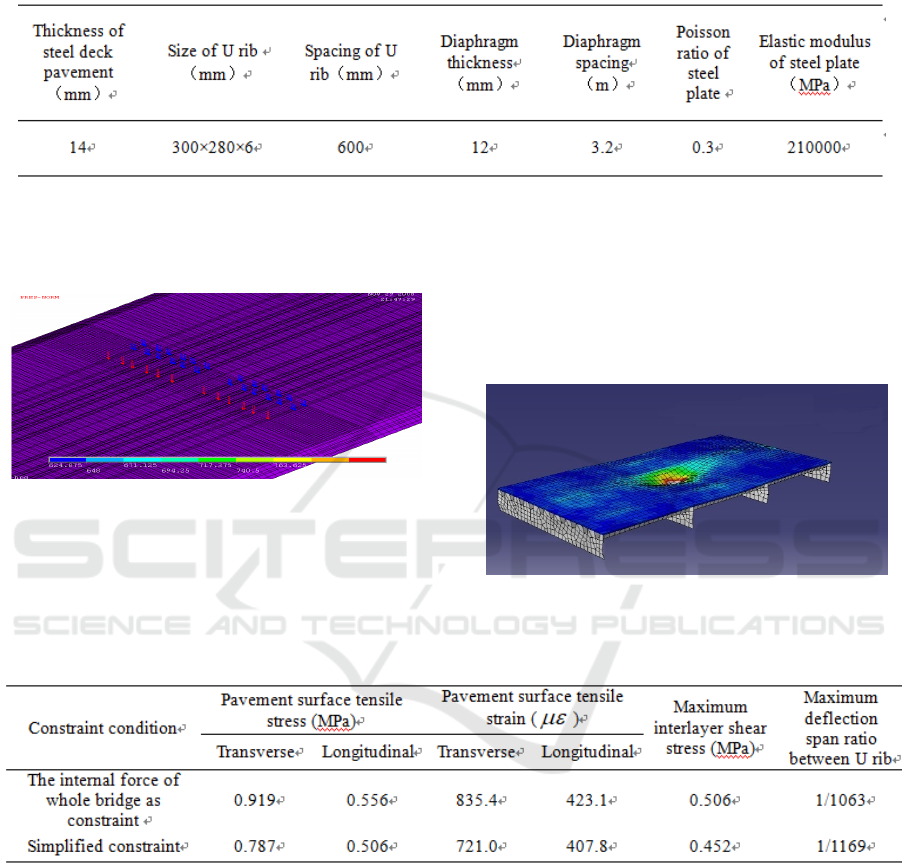
Table4:The geometric dimensions and material parameters of steel bridge deck.

The deck pavement is completely attached to the

steel bridge deck. In order to improve the calculation

accuracy, the unit near the loading area is divided

more subtly in the process of discretization as is

shown in Figure 8.

Figure 8: The composite model of bridge paving system.

The calculation and analysis of bridge paving

system considers the effect of mechanical response

of the whole three tower two span bridge. In the past

calculation, the influence of bridge characteristics

was not considered, and the boundary condition of

the model was often simplified. This paper

innovatively developed the three-stage analytical

method. The displacement value obtained by the

whole model in the previous stage is used as the

boundary condition of the local model in the latter

stage. This method can simulate the mechanical

response more accurately of the bridge deck

pavement. Figure 9 is the displacement calculation

diagram of the composite model.

Figure 9: The displacement diagram of the composite

model.

Table 5:The mechanical control index value of the composite model under the standard axial loading.

The calculation of local orthotropic plate

composite model considered two kinds of constraint

condition as Tab.5. The calculation results show that

the whole bridge structure has obvious influence on

the stress of pavement layer. The maximum stress

and strain of the composite model considered the

force situation of whole bridge is about 17% greater

than the simplified constraint model. Therefore, it

can be considered that the influence coefficient of

the bridge structure of Taizhou bridge on the local

force of pavement layer is 1.17. The main purpose of

the local orthotropic plate model calculation was to

obtain the most adverse stress, strain and

interlaminar shear stress of the deck pavement. The

calculated results can be used as the main technical

indexes of bridge pavement materials and structural

design.

5 CONCLUSIONS

This paper innovatively developed the "whole bridge

- local girder - orthotropic plate" three-stage

analytical method. Through this method, the

influence of the whole bridge characteristics is

considered when analyzing the mechanical

properties of the orthotropic deck pavement.

Therefore, the mechanical analysis of pavement

structure will be closer to the actual situation.

By the calculation of the local orthotropic plate

model, the most adverse stress, strain and

interlaminar shear stress of the deck pavement were

obtained. The maximum stress and strain of the

composite model considered the force situation of

whole bridge is about 17% greater than the

simplified constraint model. Therefore, it is

necessary to consider the whole bridge characteristic

when calculating the pavement layer. Meanwhile,

the calculated results can be used as the main

technical indexes of bridge pavement materials and

structural design.

ACKNOWLEDGEMENTS

The research work described herein was funded by

the Fundamental Research Funds for the Central

Research Institute (Grant No.2016-9020). This

financial support is gratefully acknowledged.

REFERENCES

1. Ai C, Zhang Y, Al-Kahtani M S M, 2017.

Mechanical Characteristics of Asphalt Pavement

on Bridge Deck under the Braking Force of BRT

Buses. Journal of Southwest Jiaotong University,

52(4):685-693.

2. Chen, L., Qian, Z., Wang, J, 2016. Multiscale

numerical modeling of steel bridge deck pavements

considering vehicle–pavement interaction.

International Journal of Geomechanics, 16(1).

3. Qian Z D, Jian L, Jing M M, 2005. Mechanical

analysis of asphalt concrete paving projects on steel

bridge deck. China Journal of Highway & Transport,

18(2):61-64.

4. Qian Z D, Huang W, Mao Q, 2001. Mechanical

analysis of Nanjing Second Yangtze River bridge deck

pavement. Journal of highway and transportation

research and development.,18(6):43-46.

5. Yang M, Kainuma S, Jeong Y S, 2018. Structural

behavior of orthotropic steel decks with artificial

cracks in longitudinal ribs. Journal of Constructional

Steel Research, 141:132-144.

6. Zhou Z G, Yang J J, Liu X Y, 2007. Mechanical

response of pavement layers on the steel-box-girder-

bridge deck. Journal of Changsha University of

Science & Technology.

7. Zhang M, Qian Z D, Xue Y C, 2017. Research on steel

bridge deck pavement mechanical response of Urumqi

express way. Materials Science and Engineering

Conference Series.