Research on Access Speed of the Stereo Garage Based on Queuing

Theory

Xianglei Zhu

, Shuang Lv

and Jian Meng

China Automotive Technology & Research Center,300300 Tianjin, China

Keywords: Stereo garage; Queuing theory; M/M/S; Access speed;

Abstract: With the contradiction between urban parking problems, three-dimensional garage is an effective way to

alleviate the problem of urban parking difficult, but due to the current three-dimensional garage planning

unreasonable problems, some three-dimensional garage access inefficient, three-dimensional garage

construction after the use of low and serious of the waste of resources, so the rational optimization of three-

dimensional garage vehicle access speed is particularly important. Based on the theory of queuing theory,

this paper presents a method to optimize the speed of vehicle access. Firstly, the paper analyzes the factors

influencing the access scale of the three-dimensional garage and determines the index of the access speed of

the three-dimensional garage. Then, based on the theory of queuing theory, the three-dimensional garage

access is determined and the M / M / S, The Model of Stacker with Tendency Selectivity Coefficient. And

constructs the optimization model in consideration of the tolerance of different customers. Finally, an

optimization method for improving the access speed of three-dimensional garage is proposed by selecting

different stacker and different speed calculation.

1 INTRODUCTION

At present, relevant researches have been carried out

on the three-dimensional parking at home and

abroad. Scholars conducted research on the

characteristics, scale, and access efficiency of the

three-dimensional garage. Zhou Qicai analyzed the

parking status and parking service of the three-

dimensional garage in the literature [1]. The model

discusses the application of parking space utilization

and the probability of parking rejection in a three-

dimensional garage. It also discusses the possibility

of setting a parking buffer to improve the service

effectiveness of the parking system. In the paper [2],

Jiang Daijun analyzed the mechanical characteristics

of the roadway stereoscopic garage, and analyzed

the reasons for queueing at the garage entrance and

queue and the queuing model according to the

queuing theory, and optimized the queue captain and

total service time by mentioning a new scheduling

strategy. In the paper [3], Zhou Xuesong analyzed

and compared the optimal control strategies of two

typical three-dimensional garages for access

vehicles, namely selecting different objective

functions—time and energy consumption, and

establishing their optimal control strategy for access

vehicles and their The simulation results are

analyzed to illustrate the current research status of

the optimal control strategy for the access vehicle

and its importance in the stereo garage. In the

paper[4], Xu Genning proposed four kinds of

scheduling principles in order to achieve efficient

access to mechanical parking garages, and set up a

mathematical model that takes the average access

time of the garage as the objective function. In the

paper [5], Zhou Zhiyong introduced the multi-

service channel loss system to the parking lot

queuing system, used the theory of queuing theory

and the "birth and extinction process" to establish a

probability model of vehicle parking conditions, and

improved the vehicle accessibility of the parking lot.

In the paper[6], Zhou Qicai analyzed the average

parking time for different parking uses, and

proposed the concept of parking system fluency and

its calculation method. Li Jianfeng in the paper [7]

through optimization of the genetic algorithm to

optimize the scheduling strategy of the three-

dimensional garage, established a mathematical

model with the total access time as the objective

function. Xi Zhenpeng analyzes different strategies

for accessing vehicles in the paper [8]. He chooses

the standby strategy as the main strategy, and the

parking priority at the peak is the secondary strategy

to improve the efficiency of the access garage of the

three-dimensional garage. The paper [9][10][11]

demonstrated that there is a quantitative relationship

between the service time of the stacker and the

location of the stacker according to the different

ways of location path selection, which shows a

positive correlation. And through the argumentation

of this correlation, the shortest path configuration

method is given. Therefore, the rational planning of

a three-dimensional garage and the improvement of

the operating efficiency of the three-dimensional

garage are of great significance to the promotion and

operation of the three-dimensional garage.

2 INFLUENCE FACTORS AND

INDICATORS OF STEREO

GARAGE VEHICLES ACCESS

SPEED

2.1 Influence Factors of Stereo Garage

Vehicles Access Speed

The access speed of the solid garage affects the

efficiency of the stereo garage, and it is an important

index to evaluate the service level of the solid

garage. Therefore, improving and optimizing vehicle

access efficiency of three-dimensional garage is

particularly important for the operation of three-

dimensional garage.

The influencing factors of the access speed of the

vehicle in the three dimensional garage are mainly

as follows:

（ 1 ） The number of entrances and exits for

stacking garages and stackers;

（2）The access efficiency of the stereo garage

stacker;

（3）The traffic organization around the stereo

garage.

It can be seen that if we want to improve the

access efficiency of the three-dimensional garage, it

should be analyzed from the determination of a

reasonable number of entrances and exits and the

number of stackers and the improvement of the

operating efficiency of the stacker.

When studying the access efficiency of a stereo

garage, we assume that the number of parking

spaces has been determined and sufficient. At this

time, the vehicle waiting time only needs to consider

the waiting time for the stacker service. The storage

process of the stacker is the same as the process of

picking a car, and the service rate is also the same.

Therefore, only the stored car process is discussed in

this article. The stacker crane picking process is not

described here any more. The stacker crane model is

also suitable for picking up cars. process.

2.2 Index of Access Speed of Stereoscopic

Garage Vehicles

（1）Average waiting time

The average waiting time for the parking garage

is the time from the arrival of the vehicle to the

entrance and exit, waiting in line to receive the

stacker service.

（2）The average car waiting for the captain

The average waiting queue captain for a stereo

garage is the sum of the number of vehicles that are

being serviced by the stacker and the number of

vehicles that are waiting in line to receive service.

（3）Average storage time

The average parking time for a stereo garage is

the total time from the arrival of the vehicle to the

entrance and exit, waiting in line to accept the

stacker service, and parking at the designated

location.

3 THE M/M/S STACKER MODEL

WITH REFERENCE TO THE

PREFERENCE COEFFICIENT

3.1 Basic Theoretical Analysis of the

Model

（1）Input process

1）Customer number. Assume that the number

of vehicles arriving in a stereo garage is unlimited.

The number of customers is .

2）Type of arrival. The arrival of the vehicle is a

single vehicle arrival. The time interval of arrival is

distributed in the second chapter. It has been verified

by the data and in accordance with the Poisson

distribution.

（2）Service organization

1)The number of service desks. When

considering the number of stackers, the stacker is a

service desk, and a stacker corresponds to an

entrance and exit, and how many stackers

correspond to the number of service desks.

2)Service time distribution

Each vehicle receives service, and it is placed in

a parking space at a designated location. The time at

which the vehicle receives service at the stacker is

the access time of the stacker. Because the location

of the vehicles in the garage is random, the stacker

crane access time is also random. According to the

statistical distribution of the garage service time, the

corresponding service time of the vehicle is also

approximately subject to the negative exponential

distribution [4].

（3）Queuing rules

When the vehicle arrives in the garage, if the

parking space is full, it needs to wait in line, the

queuing rule is the waiting system first to first

service, so the analysis is obtained, the stacker

service model is M/M/S model.

（4）Tendency selection coefficient

The preference coefficient is that when the

vehicle arrives at the garage, it will tend to choose

the location convenient for finding and access to the

entrance and exit, in particular, it will tend to choose

the center entrance. When more entrances and exits,

this tendency to choose more obvious. We set the

preference coefficient is

3.2 The Theoretical Analysis Process of

the Number Service Model of

Stacker

When the vehicle arrives at the garage, the actual

queuing process is relative to the stacker, as shown

in Figure 3-1.

Figure3-1 The queueing process of stacking machine.

When the vehicle arrives, it is possible to choose

a stacker exit and entry according to the actual

situation. The reason for selection is different from

driver's behavior and practice. Some drivers choose

convenient access, and some drivers choose to enter

the entry line with fewer queues.

We assign the probability that the driver tends to

choose an entry and exit, assignment is

∑

.The vehicle receives the stacker service

on the principle of first come and first served at the

entry and exit.

According to the above discussion, we do

research on queues at various entrances and exits.

Suppose that

()Nt

is the number of vehicles at

the K entry point.

{

}

() ()

Pt PNt n==

(3-1)

Where

()Nt

——Number of vehicles at the k-th

entrance at time t（veh）;

()

——The probability of the nth car at the

kth entrance and exit at time t.

In a very short time interval, there will be one of

the following four situations at the garage exit of K

garage. Firstly, there is no vehicle arrival and no

vehicle service finished. Secondly, there is only the

arrival of vehicles and no vehicle service finished;

Thirdly, three is no car arrival and a car service

finished. Fourthly, there is only one car arrival, and

there is a car service finished.

（1）Firstly, there is no vehicle arrival and no

vehicle service finished.

The probability of 0 of the vehicles arriving in a

three-dimensional garage is:

1()

ett

λο

−Δ

=−Δ+ Δ

(3-2)

The number of vehicles reaching the solid garage

is 1, but the probability of not entering the K exit is:

[]

(1 )

(1 ) 1 ( )

(1 ) ( )

te C

Ct t t

Ct t

λλο

λο

−Δ

Δ•−

=− Δ•−Δ+Δ

=− Δ+Δ

(3-3)

No car service end probability is:

1()

ett

−Δ

=−Δ+

(3-4)

So the probability of no vehicles arriving and no

vehicles being serviced is:

[

]

[

]

[][]

1(1)()1 ()

1()1()

1()

tCtt tt

Ct t t t

tC t t

λλομο

λο μο

μλο

⎡⎤

−Δ+ − Δ+ Δ −Δ+ Δ

⎣⎦

=− Δ+Δ −Δ+Δ

= − Δ− Δ+ Δ

(3-5)

Where

——natural logarithm, short-cut

process 2.71828；

——Vehicle arrival in unit time（pcu/h）；

tΔ

——Tiny time intervals（s）；

()t

——High order infinitesimal quantities

tΔ

；

——Average service time of stacker（s）；

——The probability of reaching the k-th

entrance of the arriving vehicle.

（2）Secondly, there is only the arrival of

vehicles and no vehicle service finished

At this point, the number of vehicles reaching the

garage entrance and exit is 1, and the probability of

entering the K exit is::

()

te C C t t

λλο

−Δ

Δ=Δ+Δ

(3-4)

The probability that no car has finished service

is:

1()

ett

μο

−Δ

=−Δ+ Δ

(3-7)

The probability that only one vehicle will arrive

and no vehicle service is completed ：

[

]

[

]

()1 ()

=()

Ct t t t

Ct t

λο μο

λο

Δ+ Δ − Δ+ Δ

Δ+ Δ

(3-8)

（ 3 ） There is no vehicle to arrive, only the

probability of the completion of a vehicle.：

[

]

1- +(1- ) + ( ) ( )

() ()

tC t t t te

te t t t

λλοομ

μομο

−Δ

ΔΔΔ+Δ•Δ

=Δ + Δ=Δ+ Δ

(3-9)

（4）There is a vehicle arriving and there is a

probability of completion of a vehicle service.：

[

]

+( ) =( )

Ct t te t

λο μ ο

−Δ

⎡⎤

ΔΔ Δ Δ

⎣⎦

(3-10)

According to the probability formula, the

solution is:

n 1

kn kn k

nnn

CCC

PP P

λλλ

μμμμ

−−

−

⎛⎞

=≥

⎜⎟

⎝⎠

(3-11)

And

∞

∑

(3-12)

()

PPP

∞∞

−

∑∑

(3-13)

=−

(3-14)

=−

(3-15)

( ) (1 ) n=0,1,2,

nkk

ρρ

==− L

(3-16)

Where

——The probability of having n cars at the

garage entrance；

——Stacker average service time（s）.

3.3 Basic Parameter Index Analysis of

Model

According to the above model analysis can be

obtained as follows:

（1）Average number of vehicles at the k-th

entrance (including service vehicles)

(1 )

=(1 )

(1 )

(1 ) ( )

(1 )

(1 ) 1

kn kk

kk k

nnPn

ρρ

ρρ ρ

ρρ

∞∞

∞

−

∞

==−

−

=−

−

=− =

−−

∑∑

∑



(3-17)

（2）Average queue length at the k-th entrance

()

011

(1)

qnnn

nnn

LnPnPP

ρρ

∞∞∞

===

=−= −

=−=

−−

∑

∑∑

(3-18)

（3）Average waiting time

After a vehicle arrives at a garage, the waiting

time before choosing the kth entrance to receive

service is distributed between t+dt:

()

(w =Pt t dt f t dt<<+）

(3-19)

This probability value is the product of the

following three case probabilities:

Before the vehicle arrives, there are n vehicles at

the k-th entrance, and the probability is

nkk

ρρ

（1- ）

During (0,t) there is n-1 vehicle service over time,

Its probability is

()

(1)!

−−

−

A car is being served in (t, t+) time. The probability

for all n values from 1 to n, The above

situation is established ,so：

()

(1 )

=(1 )

(1)!

()

(1 )

(1)!

=(1 )

nnt

kkk

tdt e dt

edt

ee dt

edt

ρμ

μρ

ρρ μ

ρμ

μρρ

μρ ρ ρ

μρ ρ

∞

−

∞

−

−−

−

=−

−

∑

(3-20)

()

(1 )

=(1 )

ft e

μρ

μρ ρ

−−

−

(3-21)

The distribution function for waiting time is：

(1 )

(1 ) (1 )

() (1)

Pt e dt

μρ

μρ μρ

ωμρρ

ρρ

−−

−− −−

≤= −

=− = −

∫

(3-22)

The average waiting time is:

(1) (1) (1 )

(1 )

(1 ) (1 )

kk k

w tdp w t e tdt

μρ ρ μ ρ

μρ ρ

μρ ρμ

∞∞

=≤= −−−

=− =

−−

∫∫



(3-23)

Average parking time

：

()

(1 )

=(1 )

(1 ) (1 )

ft e

μρ

μρ ρ

ρμ μ ρμ

−−

−

=+=

−−

(3-24)

At this point, we have obtained various queueing

indicators at the k-th entrance. Here

(3-25)

Where

——Average rate of arrival at the

entrance；

——The probability of reaching the k-th

entrance of the arriving vehicle；

——The average service time of the stacker

（s）

——Service strength at the k-th entrance

Assuming that the average service time of the

stacker

is fixed at this time, as the arrival rate of

the vehicle increases, the service intensity of the

stacker becomes larger and larger, thus increasing

the queue length at the k-th entrance and exit, and

increasing the average delay of parking. Garage

service is less efficient.

is the propensity selection coefficient, that is,

the probability that the arrival vehicle chooses the k-

then trance. When the garage system reaches

equilibrium, the vehicle arrives at the garage, and

the driver tends to choose the equal opportunity for

each exit. At this time, the queuing situation at each

entrance and exit converges. In the balanced state,

the service level of the entire service system can be

reflected by the queuing situation at the k-then

trance. At this time

−

The queuing indicators in the garage system can

be derived from the following formulas.

（1）Average number of vehicles in the system:

Set the number of vehicles at each entrance and

exit at any time isX1 、 X2 、 X3,…,Xm, So the

average number of vehicles in the system is：

()

nEX EX X X

EX EX EX

nn n n

== +++

=+++

=++ =

∑

(3-26)

（2）Average queue length in the system:

()

∑

(3-27)

Queue length at each entrance:

'()

qq q

LL L

∑

(3-28)

（3）Average waiting time：

For any vehicle entering the cubic garage system,

the probability that its waiting time is less than t is

given by Eqs. (3-29) and (3-30).：

() ()

Pw t CP w t

≤= ≤

∑

(3-29)

() ()

(( ))

kk kk

w tdpwt td CPwt

CtdPwt Cw

∞∞

∞

⎡⎤

=≤= ≤=

⎢⎥

⎣⎦

≤=

∑

∫∫

∑∑

∫



(3-30)

（4）Average parking time is

dw Cw

μμ

=+ = • +

∑

(3-31)

It can be seen from the above formula, When

−

, The queue status of the entire system can

be represented by the queue status of any entrance.

However because the driver of the vehicle tends to

be selective,

C does not equal

−

, but is a

constant different from

−

. Drivers will always

tend to choose entrances and exits that are easy to

access from the road into the garage area and are

convenient for parking and picking up.

3.4 Considering the User Tolerance

Optimization Model

The service level of the stereo garage is mainly

reflected by the objective indicators of average

waiting time and average queue length, but for the

same queue length and parking waiting time, the

severity of anxiety of different groups of people is

different. Tolerance time varies with individual

differences and cannot be determined by a fixed

length of time criterion.

User tolerance time is not the same for different

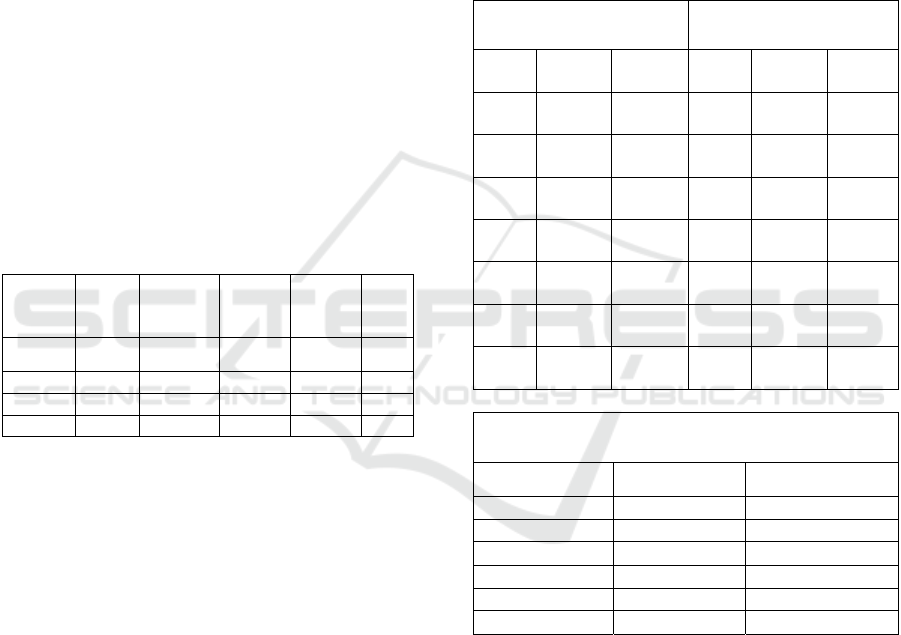
types of parking garages, It is shown in table 3-1

below.

Table3-1 The user tolerance time of garage for different

use.

Assume that the longest average waiting time

tolerated by the user is

, and the longest average

queue length that can be tolerated is

. When the

following conditions are satisfied, the optimal

number of stackers can be obtained.

(1 )

ρμ

⎧

⎪

⎨

−

⎪

−

⎪

⎩

(3-32)

Find satisfaction

max 1; ;

(1 ) 1

kk k

krqr

swwLL

λρ ρ

μρμ ρ

⎧

⎫

==<=<=<

⎨

⎬

−−

⎩⎭

this is the optimal number of stackers.

4 INFLUENCE FACTORS AND

INDICATORS OF STEREO

GARAGE VEHICLES ACCESS

SPEED

In order to optimize the access speed of stereoscopic

garage vehicles, the following two methods can be

used to reduce the average waiting queue length and

the average waiting time.

（1）Only adjust the number of stackers s.

（2）Improve the stacker service speed μ and

adjust the number of stacker s in combination.

Assume that the vehicle arrival rate during a leveling

period of a certain garage is

60 /veh h

,the peak

vehicle arrival rate is

90 /veh h

,According to

design requirements, the average time t for the

stacker to complete a car access is 75s.That is

.When there are two stackers, s=2, the

index parameters of the three-dimensional garage

are shown in the following Table 4-1.

Table 4-1 The number of stackers s = 2 when the three-

dimensional garage index table.

(veh/h)

ρk Lq(veh) W(s) d(s)

(ve

h/h)

60 0.63 1.04 125.00 200.00 60

65 0.68 1.42 157.26 232.26 65

70 0.73 1.96 201.92 276.92 70

75 0.78 2.79 267.86 342.86 75

During the peak period

60 /veh h

, the

average parking queue length

1.04

veh=

and the

average waiting time for cars are

125ws=

With the

increase in the number of vehicles arriving, it is

close to the peak,

80 /veh h

.At this time, the

average parking queue lengthis

4.17

veh=

, the

average waiting time for parking is

375ws=

.At

this time, the queue length exceeds the design

specification of the three-dimensional garage

L ≤

When the vehicle reaches peakis

90 /veh h

.At

this time, the average parking queue length is

14.06

L veh=

, the average waiting time for

parking is

1125ws=

. The average waiting time and

the average queue length are far beyond the

tolerance of customers. The service level of the

three-dimensional garage is low, and the normal

operation of the garage can no longer be guaranteed.

When the stacker crane service speed is

increased by 2%, 4%, and 8%, the index parameters

of the three-dimensional garage are shown in table

4-2 below. LetR be the rate of decrease in waiting

time from the original speed.

When the number of unused stackers is

calculated by the model, the average waiting time

for the car and the average car waiting for the

captain. The index parameters of the three-

dimensional garage when the stacker number is s=3

and s=4 are shown in the following Tables 4-2 and

4-3.

Table 4-2 List of indicators for improving the service

speed of the s=2 stacker crane.

μ increase by 2% μ increase by 4%

(

veh

)

W(s) R

(

veh

)

W(s) R

0.97 116.18 7.06% 0.90 108.00

13.60

1.31 144.95 7.83% 1.21 133.71

14.97

1.79 184.02 8.87% 1.63 168.00

16.80

2.50 240.10 10.36% 2.25 216.00

19.36

3.64 327.41 12.69% 3.20 288.00

23.20

5.69 482.09 16.82% 4.82 408.00

29.60

10.39 831.12 26.12% 8.10 648.00

42.40

μ increase by 8%

Lq(veh） w（s) R

0.83 93.35 25.32%

1.11 113.98 27.52%

1.50 140.62 30.36%

2.07 176.33 34.17%

2.94 226.71 39.54%

4.42 303.13 47.69%

When s=2, s=3, s=4, μ original speed and s=2, μ

increase speed by 2%, 4%, and 8% respectively,

wait for the captain to draw a map as the vehicle

arrival rate changes, as shown in Figure 4. -1 shows.

Figure 4-1 Relationship between arrival rate and waiting

captain.

When s=2, s=3, s=4, the average waiting time of

the car when the original speed and the speed of μ

increase by 8% are plotted as a function of the

vehicle arrival rate, as shown in Fig. 4-2.

Figure 4-2 The relation schema between arrival rate and

queue size.

When s=2, s=3, s=4, when the original speed of

μ and the speed of μ increase by 8%, the average

waiting distance of the car is plotted as the change of

the vehicle arrival rate, as shown in Fig. 4-3.

Figure 4-3 stacking machine number is not waiting for the

captain change map.

By analyzing the data in Tables 4-3 , as shown in

the data changes in Figure 4-2, Figure 4-3, when the

number of stackers s = 2, the vehicle arrival rate is

between During the change, by increasing the

service speed of the stacker, the stacker crane's

access efficiency can be significantly improved. The

average waiting time and the average waiting team

captain are all greatly reduced, and the service level

can also meet the customer tolerance. At this time,

increasing the number of stackers and optimizing the

access speed is not as obvious as improving the

service speed of the stacker. That is, there is no need

to increase the number of stackers, improve access

efficiency, and reduce energy consumption. When

the arrival rate of the vehicle changes from time to

time, the optimization effect of only increasing the

service speed of the stacker on the access speed is

not obvious. The average waiting time and the

average waiting time for the team leader are too

long, the service level is low, and the user cannot

satisfy the user. demand. Therefore, increasing the

number of stackers at this time optimizes the access

speed, which can significantly increase the access

speed and service level of the stereo garage vehicles.

The increase in the service level of the two stackers

is not obvious, so only one stacker is needed.

Due to the fact that the three-dimensional car

garages are mostly built in areas such as hospitals

and shopping malls where the traffic volume is

relatively large, it is recommended to use three

stacker cranes in actual operation. During the peak

period of non-traffic, two stacker cranes work and

fine-tune the stacker cranes. The service speed μ, the

level of service can meet most of the vehicle arrival

rate, stereo garage can be effectively run, when the

traffic peak period, when the three stacker crane

work at the same time, to ensure that the three-

dimensional garage operates at a higher level of

service . The third stacker can be used for inspection

when idle. This will not only optimize the access

speed of the three-dimensional garage, improve the

service level of the garage, but also reasonably save

energy consumption, but also ensure the rational

operation of the mechanical stacker.

5 CONCLUSIONS

This article first analyzes the factors affecting the

access speed of the stereoscopic garage, and

determines the index of the access speed of the

stereo garage. Then it establishes a model of the

number of stereo garage stackers with reference to

the selection coefficient. Under the condition of

customer tolerance, the optimization of the quantity

model of the stacker was optimized. Finally, the

vehicle access speed of the stereo garage is

optimized by changing the number of stackers and

configuring the service efficiency of the stacker.

REFERENCES

1. Zhou Qicai, Pei Ning, XiongXiaolei. Discussion on

Parking Garage Service Model and Efficiency Based

on Queuing Theory[J]. China Journal of Construction

Machinery, 2005 (2): 161-164.

2. Jiang Daijun. Research on the queuing and location

optimization of roadway stacking type three-

dimensional garage[D]. Chongqing University, 2014.

3. Zhou Xuesong, Tian Mi, Ma Youjie, et al. Research

on Optimized Control Strategy of Intelligent Stereo

Garage Access Vehicle[J]. Manufacturing Automation,

2008, 30(10): 29-34.

4. XU Gening, CHENG Hongmei, CHEN Yanwei.

Optimizing the Principle of Accessing and

Dispatching for Stereoscopic Garage Vehicles Based

on Queuing Theory [J]. Hoisting and Transport

Machinery, 2008 (5): 50-55.

5. Zhou Zhiyong, Chen Jun, Wang Wei. The acceptance

condition of parked vehicles based on queuing

theory[J]. Journal of Southeast University(Natural

Science), 2006, 36(4): 638-642.

6. Zhou Qicai, XiongXiaolei, Ren Jianqiang, et al.

Characteristic Analysis and Fluency Calculation of

Stereoscopic Parking System [J]. China Civil

Engineering Journal, 2005 (1): 41-45.

7. Li Jianfeng, Duan Wenjun, Fang Bin, et al.

Optimization of Access Parking Dispatching Based on

Improved Genetic Algorithm[J]. Control Engineering,

2010, 17(5): 658-661.

8. Xi Zhenpeng. Analysis of the Access Policy of

Stereoscopic Garage Based on Queue Theory [J].

Forum on Industry and Technology, 2011, 12: 81-82.

9. Potrc,T.Lerher, J. Kramberger, and M.Sraml.

Simulation model of multi-shuttle automated storage

and retrieval systems. Journal of Materials Processing

Technology,2004: 236-244

10. Motoji Yamamoto, Yoshiaki Hayashi and Akira Mohri,

Garage parking planning and control ofcar-like robot

using a real time optimization method[C] Proceeding

of the 2005 IEEE International ConferenceonAssem

Task Plan,July19-21,2005,Canada,2005:248-253.

11. Perry R F, Hoover S F, Freeman D R. Design of an

Automated Storage/Retrieval System Using

Simulation Modeling[J].Institute of Industrial

Engineers. ICAW Proceedings,1983: 57-63.

12. Jung S,Moon B R. Toward Minimal Restriction of

Genetic Coding and Crossovers for the 2nd

Eunclidean TSP

． IEEETrans on Evolutionary

Computation, 2002, 6 (6) : 557-565.