Calibration of Parallelism Error About

otating Shafts Based on the

Three-coordinate Measuring Machine

Xinhua Zhao

1,2,3

, Liangping Ji

1,2,3

and Lei Zhao

1,2,3

School of Mechanical Engineering, Tianjin University of Technology, Tianjin 300384, China

Tianjin Key Laboratory for Advanced Mechatronic System Design and Intelligent Control, School of Mechanical

Engineering, Tianjin University of Technology, Tianjin 300384, China

National Demonstration Center for Experimental Mechanical and Electrical Engineering Education (Tianjin University o

Technology)

Keywords: Design; accuracy; measuring machine; parallelism; error calibration.

Abstract: The three-coordinate measuring machine is widely used in advanced manufacturing technology and

scientific research. Optimized design is extremely essential for improving accuracy of measuring machine.

According to the applied coordinate measuring machine’s structure, a method is proposed to realize the

calibration of parallelism error about rotating shafts. A large number of experiment and data have proved

that the proposed theory can quickly and efficiently complete the calibration work of parallelism error about

two rotating shafts. It posses some advantages such as easy operation, high flexibility and low cost. The

efficiency of calibration is also greatly enhanced．

1 INTRODUCTION

Accuracy is an important index to measure the

quality of measurement system. The accuracy of

modern industrial processing and detection precision

demand is higher and higher in the measurement

system. It is very important to reduce the error and

improve the measurement accuracy in practical

application[1-3]. There are many factors affecting

the mechanism error, and the structural parameter

error is one of the most important factors affecting

the measurement accuracy. At present, the

commonly used error calibration method is divided

into external calibration and self-calibration[4-5].

Theoretically, the external calibration adopts

precision measuring machine to obtain higher

calibration results, but the calibration cost is

expensive[6-7]. In response to these problems, based

on the actual structure of the measuring machine, a

method is proposed to realize the calibration of

parallelism error about rotating shafts based on the

applied coordinate measuring machine’s structure,

and completes the error calibration work.

2 THE STRUCTURE OF THE

MEASURING MACHINE

The measuring machine consists of five kinematic

pairs, namely two prismatic pairs and three revolute

pairs which move linearly along the X and the Z

direction. In the rotating shaft, the -axis and the B-

axis are theoretically parallel, and the axis of the A

axis is perpendicular to the B axis. The length of the

measuring rod is 250 mm and the length of the

cantilever is 500 mm, as shown in Figure 1. Due to

the installation error of the mechanism, the rotating

shafts the -axis and the B-axis are not completely

parallel. It can be seen from the reference that the

error caused by the rotation axis has the greatest

influence on the measurement accuracy, and with

the length of the link is gradually enlarged[8-9].

Therefore, it is particularly important to solve the

problem of parallelism error between two rotating

axes.

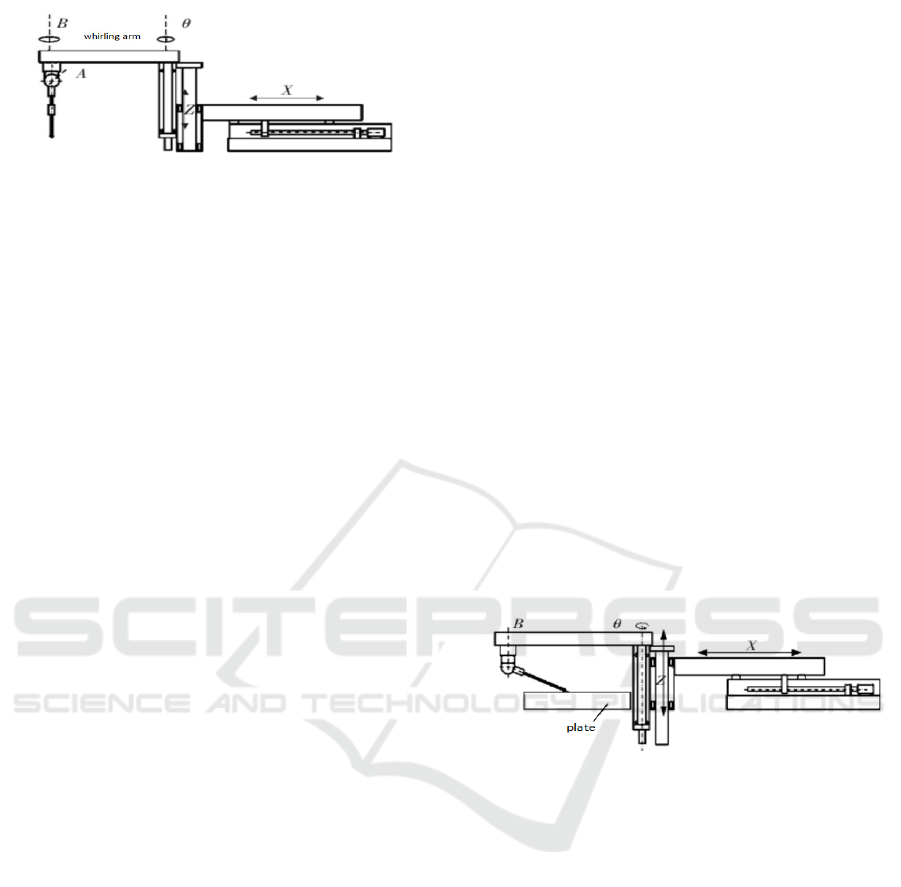
Figure 1: The structure of measuring machine.

3 PRINCIPLE OF PARALLELISM

ERROR CALIBRATION

There are many factors affecting the mechanism

error, and the structural parameter error is one of the

most important factors affecting the measurement

accuracy. At present, the commonly used error

calibration method is divided into external

calibration and self calibration. The external

calibration method is similar to the calibration

method of the traditional tandem mechanism. The

accurate external 3D measurement device is used to

estimate and calibrate the kinematic parameters of

the parallel robot. General use of laser

interferometer, theodolite and so on. The self-

calibration method is used to obtain redundancy

information about the position by the redundant joint

sensor of the parallel system. Theoretically, the

external calibration requires the use of highly

accurate precision measuring instruments or sensors,

fine adjustment and measurement results in higher

calibration results. However, the calibration cost is

high, and the actual accuracy is usually difficult to

achieve the expect effect in the worse calibration

environment. For the above reasons, aiming at the

parallelism error of rotating shaft, a calibration

method with low cost, high efficiency and low

environmental requirements is proposed in this

paper, which solves the existing problems of

external calibration.

In order to obtain the parallelism error between

the rotation axesθand B in the measuring machine, it

is necessary to obtain the perpendicularity

relationship between the two rotation axes and the

plane based on the same reference plane. It is

important to note that the accuracy of the plane is

higher than the accuracy of the measuring machine.

Therefore, using a high-precision plate as a standard

reference plane, the data detected by the probe on

the plate is obtained by rotating the two rotating

shaftsθand B respectively. By the least square

method, the perpendicularity relationship between

each axis and the reference plane, the plate can be

calculated. Finally, the parallelism error between the

two axes can be calculated.

3.1 The Perpendicularity Between the

Axis ofθand the Plate

In the measurement system, the rotation angle range

of the axisθis -120º～120º, the rotation angle range

of the axis B is 0º～360º, and the rotation angle

range of the axis A is 0º～120º. In order to measure

the relationship between the axis of the whirling arm

and the plate, the measure machine sends the probe

above the plate, as shown in Figure 2. Let the probe

be properly rearward, rotate 180ºabout the B axis

and 70ºabout the A axis. In this way, the whirling

arm can be shorten and the scanning range of the

probe can be increase; otherwise, a larger plate is

needed, and the cost is expensive.

Figure 2: Axis of whirling arm and the parallelism of Z -

axis.

The measuring rod is vertically falling down along Z

direction to the point where the measuring ball is in

contact with the plate, Rotating the rotating shaftθ,

record the coordinates of the probe on the panel

every 20°. Using the least square method fit to find

the normal direction of the forming plane, and it

represents the axial direction of the rotating shaftθ.

The two measurements date are shown in Table 1.

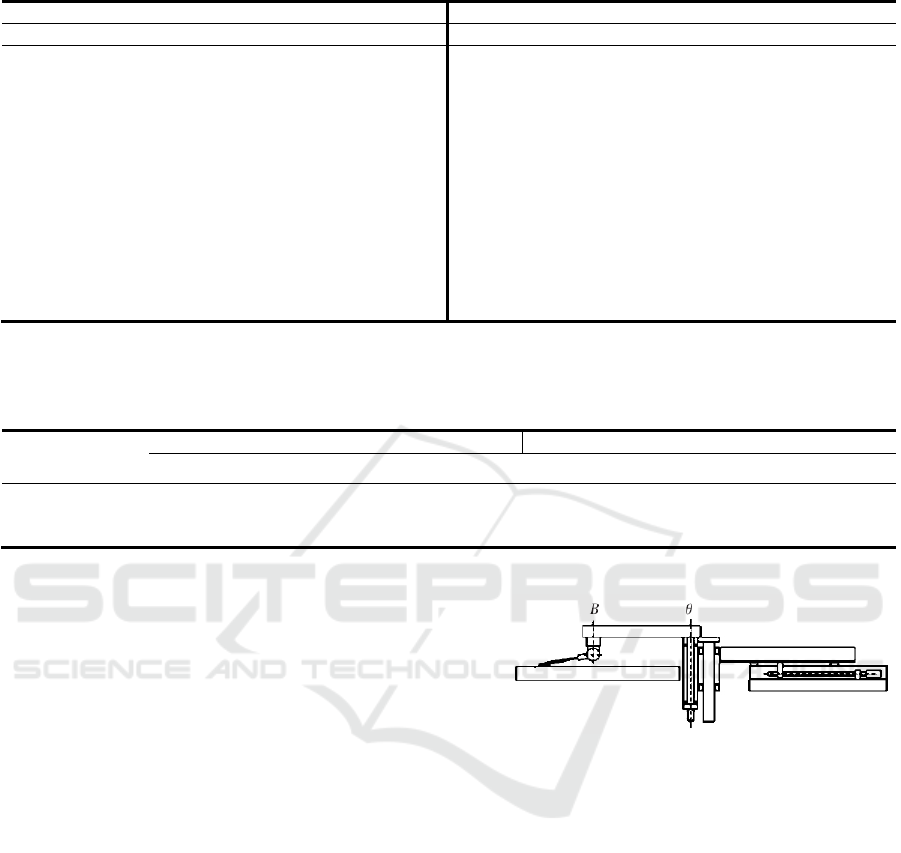
Table 1: The measurement data of whirling arm.

First measurement data Second measurement data

X/mm Y/mm Z/mm X/mm Y/mm Z/mm

652.8527 -519.2574 -103.6222 651.3632 519.9587 -99. 80469

738.4846 -459.1523 -103.4558 737.1935 460.1162 -100.0824

812.3357 -385.1113 -103.2305 811.3597 386.3012 -100.4047

872.1877 -299.3770 -102.9571 871.5892 300.7864 -100.7593

916.2238 -204.5483 -102.6344 916.0750 206.1492 -101.1384

943.1135 -103.5361 -102.2890 943.4800 105.2317 -101.5287

952.0455 0.5895 -101.9144 952.9548 1.1398 -101.9164

942.76967 104.6915 -101.5305 944.2203 -103.0000 -102.2908

915.5651 205.6187 -101.1400 917.5271 -204.0426 -102.6439

871.2652 300.3030 -100.7604 873.6930 -298.8837 -102.9623

811.2077 385.8848 -100.4026 814.0226 -384.6790 -103.2378

737.2077 459.7684 -100.0828 740.3389 -458.7936 -103.4626

652.1034 519.3504 -99.8066 655.4735 -518.6305 -103.6302

The plane normal vector value and the axis direction

of the rotate shaft and the corresponding angle of the

normal vector by fitting based on the measured data,

as shown in Table 2.

Table 2: The axis normal vector of rotation shaft θ.

Serial number The plane normal vector value Normal angle/(°)

I J K α β γ

1 -0.000675 0.003667 -1.000000 90.038693 89.789861 179.786328

2 -0.000669 0.003675 -1.000000 90.038372 89.789396 179.785929

average value -0.000672 0.003671 -1.000000 90.038533 89.789629 179.786123

3.2 The Perpendicularity Between the

Axis of Rotating Shafts B and the

Plate

The perpendicularity relationship between the axis B

of the rotating shaft and the plate is shown in Figure

3. Based on the above calibration principle and the

range of the B-axis rotation, the measuring rod is

rotated about 80°around the A-axis. The coordinate

of each point of that probe on the plate are recorded

every 10ºof rotation of the B axis, and the data of

two measurement are shown in Table 3 and Table 4.

The normal direction data of the circular section

is shown in Table 5.

Figure 3: The relationship of perpendicularity between

axis B of rotating shaft and the plate.

Table 3: The first measurement data of axis B rotation.

Rotation

angle of B

axis/(°)

X/mm Y/mm Z/mm Rotation

angle of B

axis/(°)

X/mm Y/mm Z/mm

0 556.6987 -44.1303 -103.9333 180 557.5235 404.9366 -101.0477

10 595.6403 -40.7952 -104.0142 190 518.5317 401.597 -100.9706

20 633.4609 -30.73622 -104.0426 200 480.7112 391.53569 -100.9395

30 668.9628 -14.2660 -104.0287 210 445.2132 375.06477 -100.9546

40 701.0622 8.1159 -103.9667 220 413.1104 352.6746 -101.01543

50 728.7859 35.73773 -103.8583 230 385.3833 325.0547 -101.1226

60 751.2850 67.7524 -103.7090 240 362.8753 293.0388 -101.2697

70 767.8961 103.1967 -103.5213 250 346.2632 257.5931 -101.4546

80 778.0986 140.9822 -103.3026 260 336.0622 219.8093 -101.6714

90 781.5782 179.9707 -103.0591 270 332.5765 180.8229 -101.9106

100 778.2532 218.9581 -102.8012 280 335.9122 141.8263 -102.1708

110 768.1982 256.7931 -102.5307 290 345.9676 104.0013 -102.4404

120 751.7292 292.2963 -102.2615 300 362.4361 68.4918 -102.7105

130 729.3521 324.3988 -101.9995 310 384.8170 36.3995 -102.9744

140 701.7347 352.1311 -101.7513 320 412.4334 8.6734 -103.2249

150 669.7192 374.6452 -101.5259 330 444.4498 -13.8370 -103.4527

160 634.2845 391.2501 -101.3286 340 479.8898 -30.4407 -103.6496

170 596.5041 401.4512 -101.1682 350 517.6703 -40.6397 -103.8132

Table 4: The second measurement data of axis B rotation.

Rotation

angle of

axis/

(

)

X/mm Y/mm Z/mm Rotation

angle of B

axis/(°)

X/mm Y/mm Z/mm

0 556.7003 -44.1307 -103.9356 180 557.5227 404.9366 -101.0470

10 595.6425 -40.7956 -104.0144 190 518.5330 401.5989 -100.9687

20 633.4599 -30.7400 -104.0452 200 480.7122 391.5391 -100.9380

30 668.9620 -14.2663 -104.0291 210 445.2156 375.0635 -100.9538

40 701.0631 8.1152 -103.9656 220 413.1110 352.6766 -101.0144

50 728.7844 35.7353 -103.8578 230 385.3840 325.0540 -101.1223

60 751.2892 67.7515 -103.7075 240 362.8752 293.0391 -101.2691

70 767.8984 103.1950 -103.5197 250 346.2628 257.5919 -101.4540

80 778.0968 140.9814 -103.3015 260 336.0630 219.8103 -101.6707

90 781.5806 179.9695 -103.0589 270 332.5788 180.8237 -101.9096

100 778.2512 218.9577 -102.7994 280 335.9113 141.8265 -102.1704

110 768.1989 256.7924 -102.5302 290 345.9649 104.0005 -102.4392

120 751.7310 292.2954 -102.2609 300 362.4351 68.4941 -102.7092

130 729.3484 324.3981 -101.9998 310 384.8170 36.3996 -102.9740

140 701.7326 352.1296 -101.7506 320 412.4319 8.6730 -103.2238

150 669.7200 374.6467 -101.5237 330 444.4517 -13.8363 -103.4516

160 634.2838 391.2508 -101.3288 340 479.8888 -30.4404 -103.6489

170 596.5043 401.4519 -101.1686 350 517.6717 -40.6387 -103.8132

Table 5: The normal vector of circular plane.

Serial number The plane normal vector value Normal angle/(°)

I J K α β γ

1 -0.002429 0.006443 -1.000000 90.139143 89.630848 179.605494

2 -0.002429 0.006446 -1.000000 90.139149 89.630673 179.605329

avera

e value -0.002429 0.006445 -1.000000 90.139146 89.630761 179.605412

Since the calibration of parallelism needs to

calibrate the deviations in two directions relative to

the reference plane, that is the X and Y directions,

this is different from the calibration of

perpendicularity error. Therefore, the deviation

angles of the axes of the two shafts relative to the

plate in the X and Y directions are given, as shown

in Table 6.

Table 6: The result of parallelism calibration.

Plate X-direction Plate Y-

direction

axisθ/( 〞)

-134.400 734.200

axis B/( 〞)

-485.800 -1 289.000

The axis of rotating shaft B produce an error

value is - 485.800 " in the X direction relative to the

plate and the error value is 1289.000" in the Y

direction. The deviation of the parallelism of the

rotating shaftθwith respect to the plate in the X

direction is - 134.400" and the deviation of the

parallelism in the Y direction is 734.200". Thus, the

parallelism error between the rotating shaftθand B is

362.099 " and - 572.488 2". The results show that

with the increase of the joint number and the gravity

of the mechanism itself, the parallelism error will be

amplified.

4 CONCLUSIONS

Through the above calibration method, the

calibration of parallelism error of rotating shafts can

be realized by using a high-precision plate.

Compared with the external calibration laser

interferometer, theodolite, etc. it is simple, easy to

operate, low requirements for environment, just

ensure the stability of the plate during measurement,

and the calibration cost is greatly reduced.

ACKNOWLEDGEMENTS

The authors acknowledge the National Key

Research and Development Program. （Grant No.

2017YFB1303502）.

REFERENCES

1. Zhang Guo-xiong. Three-coordinate measuring

machine [M]. Tianjing: Tianjin university press, 1999.

2. Zhang Guo-xiong. Development trend of three-

coordinate measuring machine [J]. China Mechanical

Engineering, 2000, 11(2): 222-226.

3. Wang Cong-jun, Wei Lin, Li Zhong-wei.

Mathematical modeling and calibration method of

humanoid joint coordinate measuring machine [J].

Journal of Huazhong university of science and

technology: natural science edition, 2007, 35(17): 1-4.

4. Liu Dejun, Ai Qinghui, Wang Jianlin, et

al．Kinematic calibration and computer simulation of

3 DOF parallel-links CMM［J］．Chinese Journal of

Mechanical Engineering, 2004, 40（3）: 15-19．

5. Yu Lian-dong, Cheng Wen-tao, Fei Ye-tai. Parameter

calibration method for an articulated coordinate

measuring machine with laser tracker［J］．Journal

of University of Science and Technology of China,

2009, 39（12): 1329-32．

6. Ren Yong-jie, Zhu Ji-gui, Yang Xue-you etc. The

method of calibrating robot by using laser tracker [J].

Journal of mechanical engineering, 2007, 43(9): 195-

200.

7. Ye Dong, Huang Qing-cheng, Che Ren-sheng.

Calibration of structural parameters of multi-joint

coordinate measuring machine [J]. Journal of

astronautic metrology and measurement, 1999, 19(6):

12-16.

8. Wang Ping-ping, Fei Ye-tai, Lin Chen-wang.

Optimization design of flexible three-coordinate

measuring arm precision [J]. Journal of applied

sciences, 2006, 24(4): 410-414.

9. Wang Xue-ying, Liu Shu-jia, Zhang Guo-xiong etc.

Research on calibration technology of multi-joint

flexible three-coordinate measuring system [J]. Journal

of Harbin Institute of Technology, 2008, 40(9): 1439-

1442.