Physical and Numerical Simulation of Contact Mechanics of

Spark-eroded Tool Steel with Controlled Roughness

Ignacio Cueva

, Miguel Ángel Ramírez

, Carlos Gabriel Figueroa

, Hadassa Amelia Juárez

and

Rafael Schouwenaars

Facultad de Ingeniería, Departamento de Materiales y Manufactura

Universidad Nacional Autónoma de México, Coyocacán, 04510, México.

Facultad de Ingeniería, Departamento de Materiales y Manufactura

Universidad Nacional Autónoma de México, Via de la Innovación 410,

PIIT Apodaca, Nuevo Leon, Mexico.

Keywords: Spark Erosion, Surface Roughness, Load-Displacement Curve, Contact Measurement, Finite Elements.

Abstract: Spark erosion is a convenient process to produce dies with complex shapes from hard tool materials used

under severe contact conditions. A controlled surface roughness can be produced by systematic variation of

the milling parameters. This is used in the present work to prepare surfaces for contact mechanics testing and

simulation, as will be shown by a newly developed method which performs between contact measurements

and finite element simulations of experimentally characterised rough surfaces. In the experiment, the surface

roughness of the tool steel is measured by means of optical profilometry. Using an instrumented indentation

stage, contact is made with a spherical surface and the force-displacement curve measured. The surface

geometry is measured again to detect the effect of plastic deformation. To execute the numerical simulation,

the measured surface topography is transferred, one on one, to a finite element mesh with 237169 surface

nodes. The method allows to perform precise simulation of the contact of real surfaces, instead of approximate

or numerically simulated ones, limited only by the spatial resolution of the measurement.

1 INTRODUCTION

Friction and wear of tool materials are of primary

concern in the design and operational of industrial

metal forming processes. Despite more than a century

of intensive research in this field, it can be stated that

a theoretical explanation of friction and wear has not

yet been achieved. A first problem to be solved is that

of the contact mechanics of rough surfaces. From the

first appearance of surface profilers, it was

recognised that roughness must be studied from the

viewpoint of random process theory (Whitehouse and

Archard, 1970; Nayak, 1971). A successful

incorporation of this theory into a contact models was

made by (Greenwood and Williamson, 1966), who

considered a profile consisting of spherical asperities

with a Gaussian or exponential height distribution.

These early studies considered “conventional”

geometries, in the sense that it was assumed that all

the higher moments of the power spectral density

exist. More recently, the concept of fractal or

self-affine surfaces has gained popularity (Majumdar

and Bhushan, 1990; Majumdar and Bhushan, 1991).

Using numerical simulation, it is very easy to adapt

the classical GW-model to these assumptions.(Müser

et al., 2017) present a recent review of existing

models which are either based on further refinements

of the GW-model or use finite elements, boundary

elements or molecular dynamics. The latter three

provide a more detailed description of the surface

topography. Recent modifications of asperity-based

models include new descriptions of the geometry and

elastoplastic behaviour (Wen et al., 2018; Yuan et al.,

2017), but rely on a statistical analysis of the surface,

which inherently implies significant simplification of

the real geometry, which is used in this work.

Publications on experimental contact mechanics

are relatively rare as compared to studies on

simulations and generally rely on certain statistical

parameters characterising the roughness, not on

detailed analysis of the total geometry. One

interesting exception is the study by (Bennett et al.,

2017), who used 3D-printing to create surfaces with a

180

Cueva, I., Ramírez, M., Figueroa, C., Juárez, H. and Schouwenaars, R.

Physical and Numerical Simulation of Contact Mechanics of Spark-eroded Tool Steel with Controlled Roughness.

DOI: 10.5220/0008187301800183

In The Second International Conference on Materials Chemistry and Environmental Protection (MEEP 2018), pages 180-183

ISBN: 978-989-758-360-5

prescribed topography and observed the contact area

through a transparent contacting surface.

Apart from the latter example, in general it is not

self-evident to create surfaces with controlled random

roughness characteristics. Many surface preparation

techniques will generate patterns which are either

periodic or strongly anisotropic. Isotropic randomly

rough surfaces with controlled roughness parameters

have been prepared by sand blasting,

electrodeposition and spark erosion. Several authors

have shown how the control of electrical discharge

parameters can produce surfaces with controlled

roughness and fractal parameters (Singh et al., 2004;

Deltombe et al., 2014).

2 EXPERIMENTS AND

SIMULATIONS

Commercial D2 steel was prepared by spark erosion

using an EDM444M3-L numerically controlled

electrical discharge equipment with a 15 mm

diameter electrolytic copper electrode. For the

example presented in this text, a depth of 0.1mm was

eroded using 10 ms pulses of 0.8A with a 65% dead

time between pulses.

Surface topography was measured by a Nanovea

optical profilometer using Chromatic Confocal

Technology before and after contact testing. Contact

testing was performed on the same system by

pressing a spherical stainless steel stylus of 2.5mm

radius onto the measured surface at a velocity of 0.25

N/min until reaching a load of 0.5N. According to

Hertz contact theory, this allows to maintain the bulk

of the sample within the elastic region. The

measurement of the surface roughness and surface

indentation were centred by creating and indentation

in a soft copper specimen and calculating the distance

between the centre of the stylus and the centre of the

optical pen. This analysis also allows verifying any

possible damage to the spherical surface of the stylus

by measuring the surface profile of the indentation

made in the copper sample.

The measured surface was analysed by means of

earlier developed software to determine the fractal

dimension (Schouwenaars et al., 2017), roughness

and height distributions. The measured geometry was

introduced into the ABAQUS Explicit Finite Element

Package by creating a mesh with a smooth surface

and substituting the height values of the surface

nodes with the measured ones. The surface roughness

was scaled in such a way that the maximum height

difference was equal to 1/2 of the size of the elements

used in the contact zone. This procedure is valid if all

results are scaled accordingly.

3 RESULTS AND DISCUSSION

The mean square roughness of the surface analysed in

this work was equal to 5.8

as determined by the triangular prism method, was

equal to 2.8. The bearing curve, i.e. the empirical

(cumulative) distribution of the surface heights, is

given in Figure 1, both before and after the contact

test. Small differences between both curves indicate

that some plastic deformation occurred during the

test.

Figure 1: Cumulative height distribution before and after

contact testing and Gaussian fit.

Figure 2 presents the measured surface heights

before (Figure 2a) and after (Figure 2b) the test.

Figure 2c) shows the difference of the height profile

before and after testing. To eliminate small shifts in

the horizontal position of the measurements, a

least-squares procedure was used. No clear pattern

can be observed in Figure 2c, indicating that plastic

deformation was very small. A low pass filter applied

to the three images in Figure 2 revealed that the

surface shows a broad maximum in the upper-right

quarter of the measured zone which was slightly

depressed as the consequence of plastic deformation

during the test. This small difference is also seen in

the height distributions of Figure 1.

Physical and Numerical Simulation of Contact Mechanics of Spark-eroded Tool Steel with Controlled Roughness

181

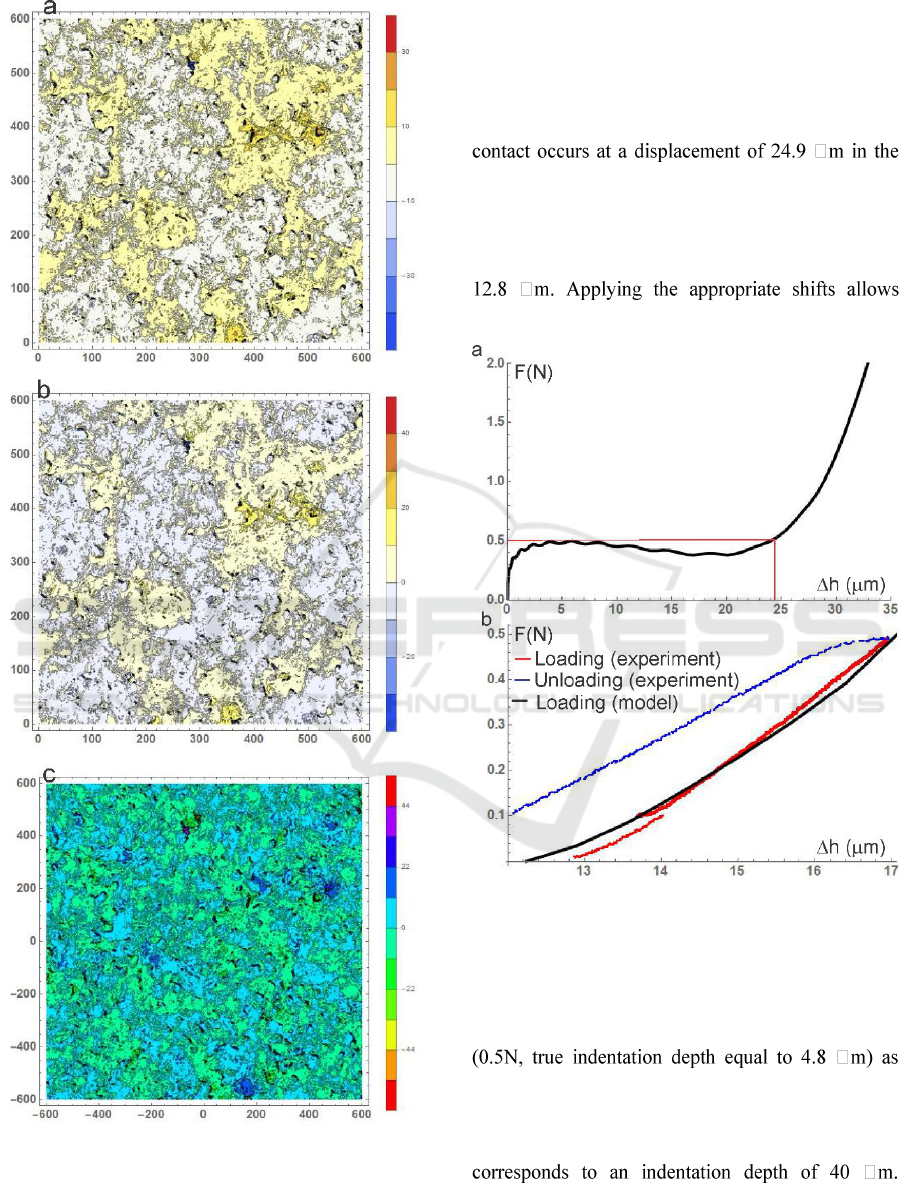
Figure 2: a) shows the surface profile before testing, b)

shows the same after testing, c) gives the height differences

due to the indentation. The difference pattern is almost

random, with a slight tendency to negative values,

indicating only small plastic effects were present.

An example of the finite element results is given

in Figure 3. Figure 3a shows the raw

load-displacement curve after scaling. Some initial

fluctuations are due to the explicit integration

scheme, the small load before contact corresponds to

the weight of the contacting body. The point of first

model.

Figure 3b shows the experimental loading and

unloading curves, with evidence of a small plastic

deformation, as the unloading curve is shifted to the

left. The point of first contact occurs at approximately

comparing model to experiment.

Figure 3: a) shows the modelled curve without correction

for dynamic effects and instrument weight. b) compares the

corrected curve to the measured ones. The shift applied to

obtain Figure 3b is marked by the red reference lines in 3a.

Figure 4 shows the contact pressure distribution.

4a corresponds to the situation at maximum load

shown in Figure 3b. It is seen that only a small

number of asperities contacts the spherical stylus. 4b

is added to provide a clearer view of how such a

contact distribution looks at higher loads. The image

Evidently, considerable plastic deformation would

occur at these loads, which is not taken into account

MEEP 2018 - The Second International Conference on Materials Chemistry and Environmental Protection

182

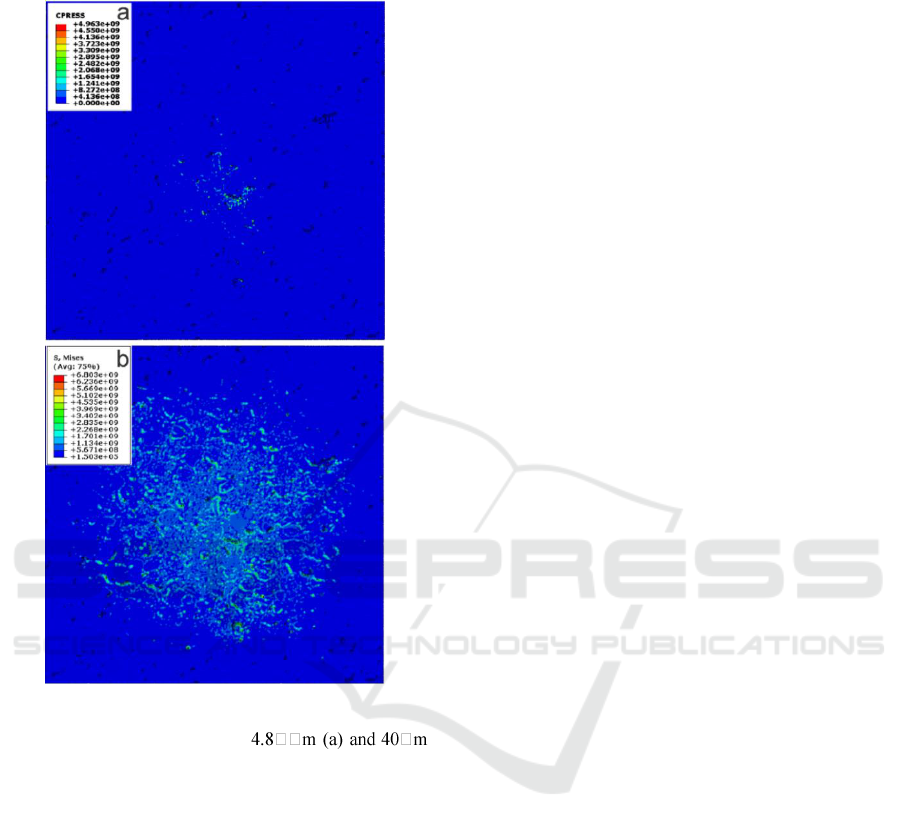
in the present simulations but can be incorporated

into future experiments and models.

Figure 4: Contact pressure distribution as predicted by the

model at an indentation depth of

(b).

4 CONCLUSIONS

Spark erosion can generate randomly rough surfaces

with controlled roughness and a high fractal

dimensions. Combining standard equipment for

instrumented indentation with an optical surface

profiler mounted on the same console, precise

measurements of contact load-displacement curves

can be combined with a detailed analysis of the

surface topography before and after testing.

Using purposely developed software, the

measured surface can be superposed on a pre-existing

finite element mesh. The measured geometry and the

finite element geometry are the same, the only

limitation is the spatial resolution of the

measurement. This is a significant innovation and can

be used in future, more extensive studies in which the

surface roughness will be varied through systematic

analysis of the electric discharge parameters.

ACKNOWLEDGEMENTS

Financial support from DGAPA projects PAPIIT

IN114718 and PAPIME PE111018 is acknowledged.

MA Ramírez and CG Figueroa thank DGAPA for

their post-doctoral fellowships. HA Juárez thanks

CONACYT for her master’s scholarship.

REFERENCES

Bennett, A.I., Harris, K.L., Schulze K.D., Urueña, J.M.

McGhee A.J., Pitenis A.A., Müser M.H., Angelini,

T.E., Sawyer,W.G., 2017. Contact measurements of

randomly rough surfaces. Tribology Letters 65, 134.

Deltombe, R., Kubiak, K. J., Bigerelle, M., 2014. How to

select the most relevant 3D roughness parameters of a

surface. Scanning: The Journal of Scanning

Microscopies, 36, 150.

Greenwood, J.A., Williamson, J.B.P., 1966. Contact of

nominally flat surfaces. Proceedings of the Royal

Society of London A, 295, 300.

Majumdar, A., Bhushan, B., 1990. Role of fractal geometry

in roughness characterization and contact mechanics of

surfaces. Journal of Tribology, 112, 205.

Majumdar, A., Bhushan, B., 1991. Fractal model of

elastic-plastic contact between rough surfaces. Journal

of Tribology, 113, 1.

Müser M.H., Dapp W.B., Bugnicourt R., Sainsot P.,

Lesaffre N., Lubrecht T.A., Persson B.N., Harris K.,

Bennett A. et al., 2017. Meeting the contact-mechanics

challenge. Tribology Letters. 65, 118.

Nayak, P.R. 1971. Random process model of rough

surfaces. Journal of Lubrication Technology, 93, 398.

Schouwenaars, R., Jacobo V.H., Ortiz A., 2017. The effect

of vertical scaling on the estimation of the fractal

dimension of randomly rough surfaces. Applied

Surface Science. 425, 838.

Singh, S., Maheshwari, S., Pandey, P.C., 2004. Some

investigations into the electric discharge machining of

tool steel using different electrode materials. Journal of

materials processing technology, 149, 272.

Wen Y, Tang J, Zhou, W., Zhu, C., 2018. An improved

simplified model of rough surface profile. Tribology

International 125 75.

Whitehouse, D.J., Archard, J.F., 1970. The properties of

random surfaces of significance in their contact.

Proceedings of the Royal Society of London. A. 316,

97.

Yuan Y, Cheng Y, Liu, K., Gan, L., 2017. A revised

Majumdar and Bushan model of elastoplastic contact

between rough surfaces. Applied Surface Science. 425,

1138.

Physical and Numerical Simulation of Contact Mechanics of Spark-eroded Tool Steel with Controlled Roughness

183