
A Comparison of Tidal Zoning Model for the Depth Reduction
Danar Guruh Pratomo
1
, Eko Yuli Handoko
1
and Duty Kendartiwastra
1
1
Geomatics Engineering Department, Faculty of Civil Engineering, Environment, and Geo-Engineering, Institut Teknologi
Sepuluh Nopember, Surabaya, Indonesia
Keywords: Tidal Zoning, Tidal Constituent, Residual Interpolation
Abstract: Bathymetric information is essential for navigational purpose. The depth in navigational charts has to be
referred to a vertical datum with the intention of ships can navigate safely. Tide plays important rule in a depth
reduction in order to provide bathymetric information. Tidal characteristics are unique for any different places.
The tidal phase and amplitude propagation may cause difficulties in predicting water levels. The research
utilized Tidal Constituent and Residual Interpolation methods to estimate the tide propagation and to achieve
a smooth tidal zoning. Tidal constituents at each of observation point are calculated using the least squares
method and interpolated based on Laplace formula. The tidal zoning model that has been developed then was
compared to the Finite Element Solution 2014 Global Tide Model. The results show that the correlation
coefficient between those models is 0.78. Based on the research, the tidal zoning model can be used to improve
the global tide model.
1 INTRODUCTION
Seafloor information is important for supporting
marine activities (safety of navigation, demersal
fishing, offshore oil exploration and drilling, cable
and pipeline laying maintenance, and underwater
warfare). A depth measurement is the main activity to
determine the topography of the seabed. The
measured depth must be corrected by the tides so that
it refers to a chart datum. Corrected depths are the
basic information to generate a nautical chart. The
chart can also be utilized for a shipping safety and
construction of docks purposes. Due to the
importance of a chart datum in reducing depth, the
determination of the vertical datum must be
conducted accurately and precisely (Hellequin, et.al,
2003). The accuracy of a chart datum in a certain area
depends on the tide observation process and the
determination of tidal characteristics. The range
between tidal stations or between tidal station and
survey area may also affects the accuracy as it creates
a tide zonation. The determination of the tide zonation
can improve the accuracy of the tide correction for the
depth reductions.
The study discussed the simulation of a tidal
zoning using the TCARI (Tidal Constituent and
Residual Interpolation) approach. TCARI uses an
interpolation method from tide data at several tide
stations. The method applies Laplace equation to
simulate the tide on a weighted grid area model
(Cisternelli and Gill, 2005). Each point on grid has a
unique tide phase and amplitude which can be used to
predict the water level at a certain position and time.
The advantage of this approach is that the
discontinuities of the tide observation which occur in
the transition zone can be eliminated. The method can
separate the calculation of water level due to tidal and
non-tidal effects (weather and river discharge) and
can also display model uncertainty due to tidal datum,
astronomic, and water level uncertainty errors
(Cisternelli, et.al, 20017).
The research also examined the results of the tide
model from TCARI and the Finite Element Solution
2014 global tide model (FES2014). FES2014
represents tidal cycles across the globe. This model is
derived from several altimetry satellite missions
(Cancet, et.al, 2017). Based on the comparison
between these models, it is expected that tide model
from TCARI can improve the accuracy and the
resolution of the global tide model FES2014
especially on the coastal area.
50
Pratomo, D., Handoko, E. and Kendartiwastra, D.
A Comparison of Tidal Zoning Model for the Depth Reduction.
DOI: 10.5220/0008373900500054
In Proceedings of the 6th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management (ISOCEEN 2018), pages 50-54
ISBN: 978-989-758-455-8
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 METHODS
The research is located in Makassar Strait, the strait
between Kalimantan and Sulawesi which is
connected to Pacific Ocean in the north and adjacent
with Java Sea in the southern part. The geographical
location of the research area stretches from
115°25'03.7"E to 120°00'34.8"E of the longitude and
from 05°30'04.8"S to 00°57'52.36"N of the latitude
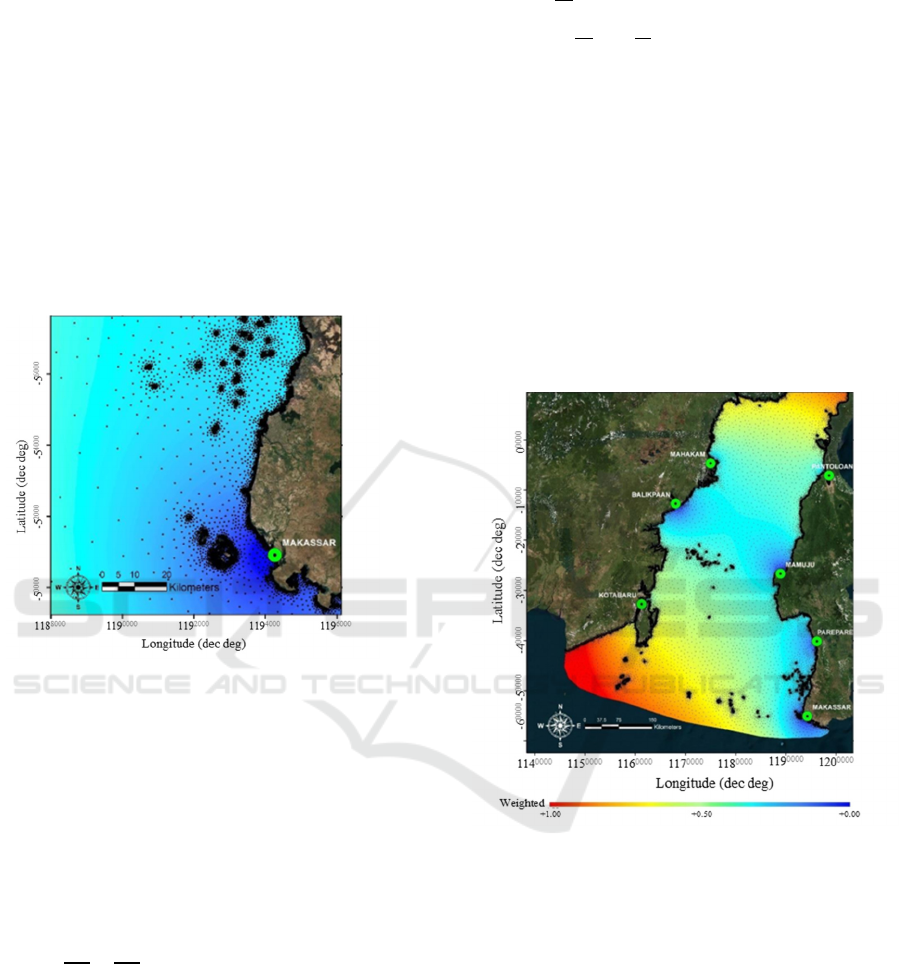
(red line in Fig. 1).
Figure 1: The research area located in Makassar
Strait
The research used 7 tide stations in the proximity
of the area of interest (yellow triangles in Fig. 1). The
tide observations data from these stations are
provided by Indonesia Geospatial Information
Agency (2017). The data is then processed based on
10 minutes to obtain tide constituents at each tide
stations. The geographical coordinates of the tide
stations can be seen in Table 1.
The tide constituents from the tide stations are
interpolated using TCARI method. The Pydro
(Python and Hydrography) software was utilized to
generate the tidal zoning in TCARI method.
Table 1: Tide Station Coordinate
Number Station Name
Easting
(dec deg)
Northing
(dec deg)
1 Pantoloan 119.857E -0.712S
2 Mamuju 118.893E -2.667S
3 Pare-pare 119.620E -4.014S
4 Makassar 119.417E -5.112S
Number Station Name
Easting
(dec deg)
Northing
(dec deg)
5 Kota Baru 116.146E -3.291S
6 Balikpapan 116.806E -1.272S
7 Mahakam 117.399E -0.553S
The boundary for the model is derived from the
medium resolution of GSHHG. The GSHHG is a
high-resolution geography data set, amalgamated
from World Vector Shorelines (WVS) and CIA
World Data Bank II (WDBII) (Wessel and Smith,
1996). The data contains coastline and islands in shp
format. The model boundary for the model is a closed
polygon. The open ocean boundary for the model is
delineated from the area which is adjacent with
Pacific Ocean and Java Sea. In Fig. 2 shows the
coastal boundary is represented by green line and the
open ocean boundary is represented in blue line.
Figure 2: The boundary of the model
Tidal constituents at each tide station are arranged
in a .txt file in a format that can be read in Pydro. The
file also includes additional information such as the
results of vertical datum calculations (MHHW,
MHW, MLW, MLLW, and MSL). In this case MSL
(Mean Sea Level) was used as a vertical reference for
each tide stations. Note that amplitude and phase
formats follow the format from NOAA and for
constituents with 0 value will not be modeled. This
research used 11 tidal constituents; K1, O1, P1, M4,
MS4, MF, MM, M2, S2, K2, and N2.
There are several tide stations located not exactly
at the shoreline, due to the shoreline resolution. Thus,
the position of the station is shifted so that it intersects
A Comparison of Tidal Zoning Model for the Depth Reduction
51
to the shoreline. This used an assumption that the
shifting positions have the same tide regime with the
tide actual stations.
The model used TIN (Triangular Irregular
Network) with 9900 nodes and approximately
255268.763 square kilometers of model domain. The
distribution of nodes is organized so that areas close
to the shoreline and islands’ boundaries have denser
distribution than other areas. The nodes distribution
for the model can be seen in Fig. 3. The nodes
distribution considers geometry of the beach, bay, and
headland which affect local effects such as wind and
currents which indirectly influence the hydrodynamic
characteristics in the research area.
Figure 3: The distribution of nodes used in the
model
The tidal amplitude and phase from each tidal
station are interpolated and iterated using Laplace
formula. The calculation process was performed for
each node. To speed up the iteration and effectiveness
of storage space (memory), the formula is simplified
as follows (Cisternelli, et.al, 2007):
(1)
= 0 (2)
,
,
(3)
Where m is the index of the tidal stations, G is the
value of the amplitude and phase at a node and x, y is
the position of the node in cartesian coordinates
system which will be calculated its magnitude. A
weighted parameter was applied to improve the
equation. The weighted parameter was generated
based on the boundary configuration. The following
formula shows the weighted parameter applied in
Laplace formula:
0 (4)
ĝ
(5)
01
Formula 4 was applied at points located on the
coastline where the interpolated value is known.
Formula 5 was applied at points where interpolation
values want to be determined. is the direction of a
node with respect to a shoreline. α is a constant which
affects the contour. The weighted parameter ranges
from 0 to 1. The farther from the tide station, the
weighted value will be close to 1. This means the
predictive data is more accurate when the radius of
the place to the tide observation point gets closer.
Thus, this range can be a representation of the
uncertainty level of the tide model. Fig. 4 shows the
weighted distribution of the model.
Figure 4: Weighted distribution of the model
The step after a computation using Laplace
formula is extracting the co-amplitude and co-phase
of the tide using TCARI. The co-amplitude and co
phase of every tidal constituents are computed using
interpolation method. Fig. 5 is one of the example of
the co-amplitude and co-phase from K1 constituent.
This co-tidal chart of K1 constituent is created using
TCARI method. The co-amplitude is represented with
colors gradation and the co-phase is represented by
white lines. Other tide constituents are extracted
using the same technique used to develop the K1 co-
tidal chart.
,
,,
1
0
ISOCEEN 2018 - 6th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management
52
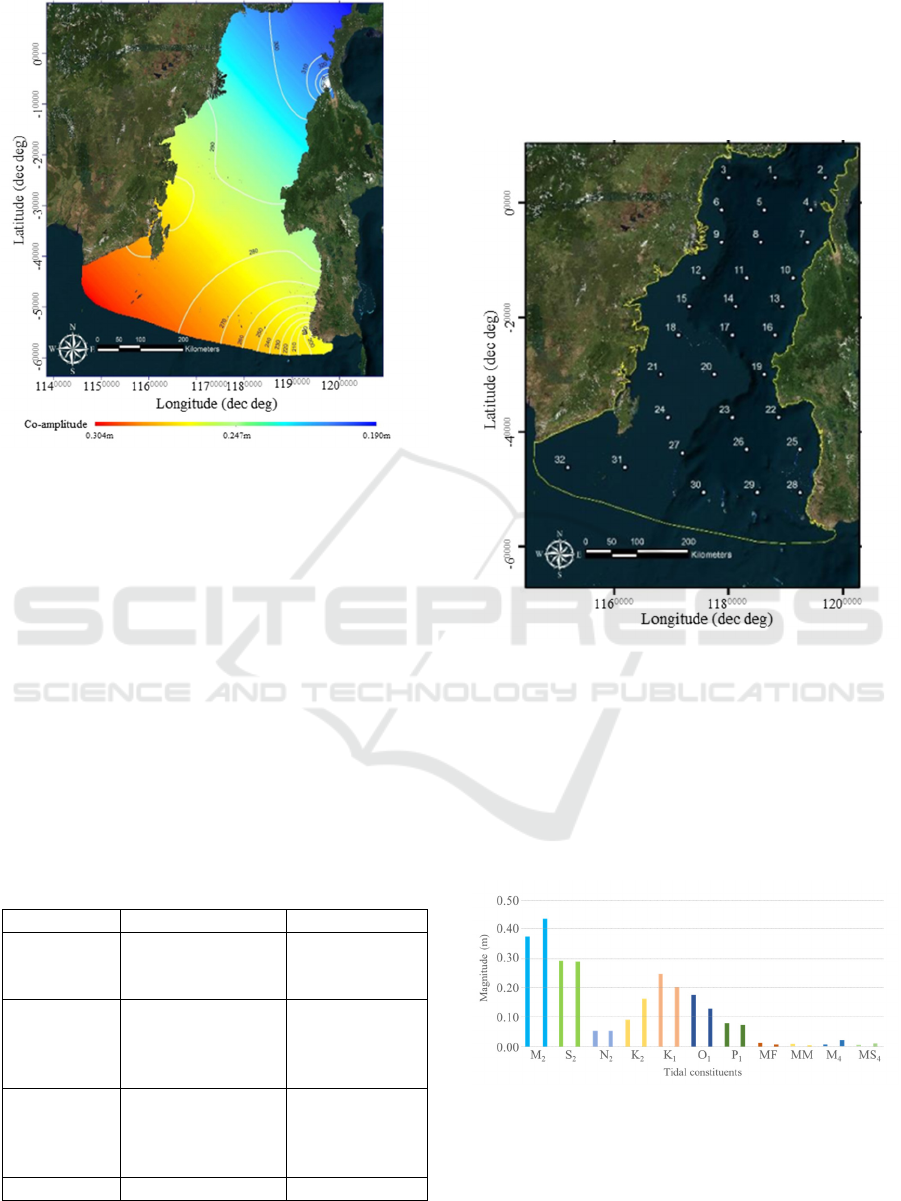
Figure 5: Co-amplitude and co-phase of K1
3 RESULT AND DISCUSSION
The research compared the tide model from TCARI
to the FES2014 model. The comparation is performed
to analyze the co-tidal chart pattern of each model.
This process aims to test the quality of the TCARI
tide model. FES2014 is developed from tide
observation data collected using satellite altimetry
whereas TCARI is generated by interpolating in-situ
data. Both models should show the same tide pattern
in the research area. However, these methods have
weaknesses and strengths which can be seen in Table
2.
Table 2. Comparation between FES2014 and TCARI
Parameter FES2014 TCARI
Observation
Time
Interval
Depend on cycle
period of satellite
altimetry mission
Up to 1 hour
Quality base
on
characteristic
area
Good in off-shore,
not really good in
near-shore.
Good in near-
shore and not
really good in
off-shore.
Observation
Continuity
Consistent (for
along years)
Inconsistent
(depends on tide
gauge
accuration)
Scale Global Local to Global
The difference in Table 2 causes inconsistent
variations in TCARI and FES2014 tide constituent
values, depending on the position of the points
compared. Correlation values were obtained from 32
Independent Check Points that had been spread
evenly in the study area as in Fig. 6.
Figure 6: Independent Check Points
Figure 7 shows the average between the FES2014
and TCARI amplitude values for each tidal
constituent at 32 ICP points. The correlation
coefficient shows a strong relationship to the diurnal
and semidiurnal tidal constituents. Whereas for the
long period tidal constituents between TCARI and
FES2014 have magnitude close to 0 (Fig. 7).
Figure 7: Average of Amplitude Value in
Independent Check Points
The small values of the MS4, M4, MF and MM
constituents are influenced by Rayleigh criteria. The
Rayleigh criteria is if there are two components A and
component B can only be separated if the length of
the data is more than a certain period called the
A Comparison of Tidal Zoning Model for the Depth Reduction
53
synodic period. The synodic period can be formulated
by the following formula (Hess, 2004):
(7)
PS= Synodic Period (hours)
= Angular Velocity of A Component (ͦ /hour)
= Angular Velocity of B Component (ͦ /hour)
Based on the formula 7, the observed period
values for distinguishing spectral MS4 and M4 are
4.310 months and for distinguishing MF and MM
spectral, a minimum observation time of 27.076 days
is required. Thus, because the length of observation
used varies at each station, which is only about 3 to 7
months, it is considered less ideal for extracting the
M4 and MS4. However, this is ideal for extracting
MM and MF. The small MM and MF magnitudes are
possibly caused by other factors, for example the
influence of the position of the Makassar Strait which
is located at the equator. Considering that MM and
MF are long-term conditions that are influenced by
the declination of the moon, this made MM and MF
are minimum at near equator. Based on 11 tidal
constituents that have been modelled, the K1 has a
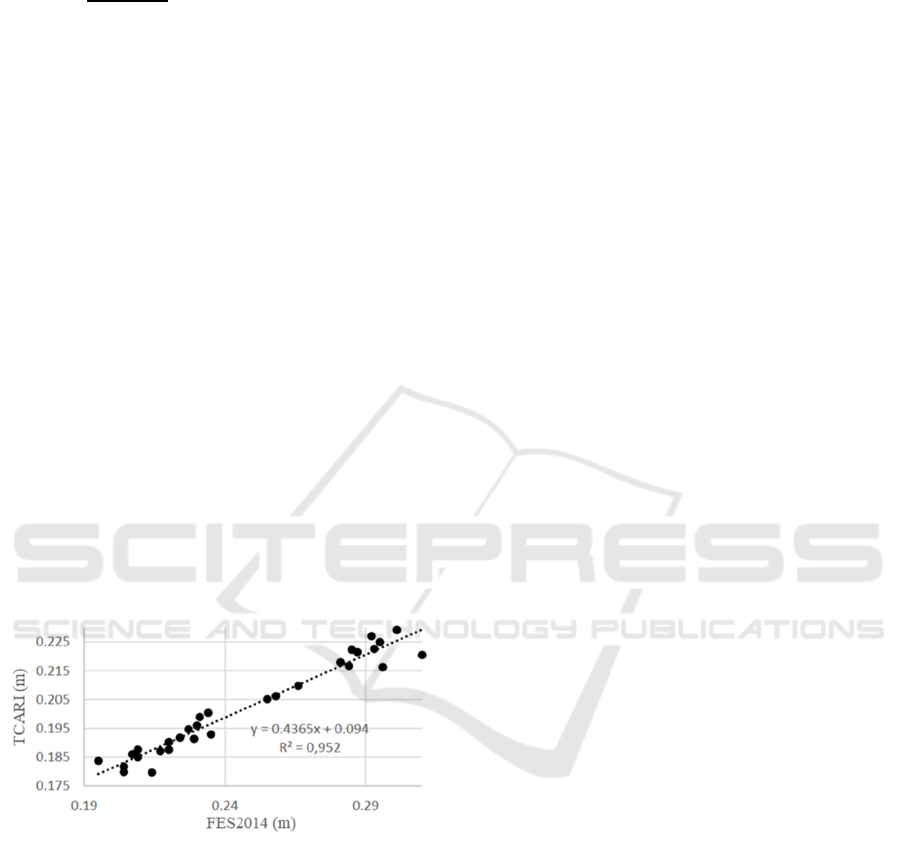
strongest correlation between TCARI and FES2014.
Fig 8 shows the coefficient correlation between the
models. The magnitude of their correlation is 0.976.
Figure 9: The coefficient correlation between
TCARI and FES2014 for K1 constituent
4 CONCLUSION
The tidal zoning model generated using the TCARI
method was compared with the global tide model
FES2014 to test the accuracy and precision of the
model. Based on the correlation test that has been
carried out on both models, the tide constituents of
S2, N2, K2, K1, O1, P1, and M2, have correlation
coefficient of 0.78. The best correlation is shown by
the pattern of K1 values with a correlation coefficient
of 0.95. The TCARI method can display smoother
tide models than the global tide model FES2014.
Tidal zoning model developed using TCARI might be
used to improve the resolution of global tide models
for the future purposes.
REFERENCES
K. Hess, 2004. NOAA technical report NOS CS. V 4.
L. Hellequin, J.M. Boucher, X. Lurton, 2003. IEEE J.
Oceanic Eng. E 28, 1.
M. Cisternelli, S. Gill, 2005. U.S. Hydrographic
Conference.
M. Cisternelli, C. Martin, B. Gallagher, R. Brennan,
2007. U.S. Hydrographic Conference.
M. Cancet, F. Lyard, D. Griffin, L. Carrère, N. Picot,
2017. 10th Coastal altimetry workshop, Italy.
Indonesia Geospatial Information Agency, 2017.
http://tides.big.go.id.
P. Wessel, W. H. F. Smith, 1996. J. Geophys. Res., B
4, 101, pp. 8741-8743.
360
ISOCEEN 2018 - 6th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management
54
