Using Technology in Mathematics Discover and Proof Pythagorean

Theorem with GeoGebra

Muhammad Naufal Faris

State University of Malang, Malang, Indonesia

Keywords: GeoGebra, Mathematics, Pythagorean Theorem, Discover, Proof.

Abstract: Pythagoras, one of the most famous ancient Greek philosophers and mathematician. One of the great

contributions to science was the Pythagorean Theorem. It states that the square of the hypotenuse is equal to

the sum of the squares of the other two sides. The theorem Pythagoras be written as an equation relating the

lengths sides c, b, and a, often known the "Pythagorean equation" a2 + b2= c2. The evidence of the

Pythagorean Theorem varies greatly. There are various ways to prove the Pythagoras Theorem a simple and

complex even in the digital era can use of technology. In the 21st century the use of technology as a source

of learning development. In Mathematics GeoGebra is free software and open source. Mathematics learning

can be studied like algebra, geometry, calculus, and statistics. GeoGebra is an interactive software for study

mathematics. The paper presents illustrate how we can use GeoGebra to guide learners in the processes of

discovering and prove The Pythagorean Theorem. Teachers or students can improve their own knowledge of

instruction for effective learning in 21-century learning.

1 INTRODUCTION

One of the first theorem when studying mathematics

in primary school is the Pythagorean Theorem. The

theorem is a mathematical statement that still requires

proof and the statement can be shown its truth value.

Pythagoras is one of the most well recognized

mathematicians (Parada-Daza and Parada-Contzen,

2014). Although his figure and influence transcend

the strictly mathematical. Throughout his life, he

liked to travel to various places, such as Egypt and

Babylon. Pythagoras taught students that everything

in the universe can be expressed in numbers. Because

of this, Pythagoras and his followers adore numbers

and ratios that can be expressed by these numbers.

The Pythagorean Theorem indicates that the square of

the hypotenuse of a right triangle equals the sum of

the squares of the lengths of the other two sides each.

a^2+b^2=c^2 where c describes the length of the

hypotenuse, a and b the lengths of the triangle's other

two sides. The theorem that may be familiar to most

people. A simple basic theorem, interesting and very

useful to learn.

The evidence of the Pythagorean Theorem varies

greatly. Bogomolny (2016) Presented there are a lot

of various ways to prove the Pythagorean theorem a

simple and complex even. In the digital era can prove

the Pythagorean use of technology. The use of

computers has been applied to learning such as in the

use GeoGebra Software the mathematics field. This

paper presents illustrate how we can use of GeoGebra

to guide learners in process of discovering and prove

the Pythagorean Theorem. Teachers or students, to

help them improve their knowledge own instruction

and effective learning.

2 DISCOVERING

PYTHAGOREAN THEOREM IN

REAL LIFE

The Pythagorean Theorem is closely related a square

shape. If a and b are the lengths of the legs of a right

triangle, c is the length of the hypotenuse, then the

sum of the squares of the lengths of the legs is equal

to the square of the length of the hypotenuse. This

relationship is described by the formula:

a^2+b^2=c^2. Let's look at the Pythagorean Theorem

form on right triangle.

Faris, M.

Using Technology in Mathematics Discover and Proof Pythagorean Theorem with GeoGebra.

DOI: 10.5220/0008407200210025

In Proceedings of the 2nd International Conference on Learning Innovation (ICLI 2018), pages 21-25

ISBN: 978-989-758-391-9

Figure 1: Right triangle ABC.

Answers :





 



 



4



3



5



16  9  25

This theorem only applies to an angled triangle.

The sum of the squares of the lengths of both legs is

equal to the square of the length of the hypotenuse

side. As discovered by (basic-mathematics.com,

2016) John leaves school to go home, He walks 6

blocks North and then 8 blocks west. How far is John

from the school? Here is how you can model this

situation.

Figure 2: Representation of Pythagorean theorem.

Answer:

















6



8







3664

 

√

100

  10

10

The Pythagorean Theorem explains in any right

triangle, the sum of the squares of the lengths of the

triangle’s legs is the same as the square of the length

of the triangle’s hypotenuse. This theorem is

represented by the formula c^2=a^2+b^(2 ). Easily, if

we know the lengths. On two sides of a right triangle,

we can apply the Pythagorean Theorem to find the

length of the third side. Understanding, this theorem

can work for right triangles.

3 GEOGEBRA

The use of technology is an important tool for

students in learning mathematics. The importance of

using technology in teaching mathematics has been

supported by the National Council of Mathematics

Teachers (National Council of Teachers of

Mathematics, 2000). Technology is an essential

component of the environment. One interesting tool

that can be used is GeoGebra.

GeoGebra is a computer program that can be used

in mathematics learning when users learn geometry,

statistics, algebra, calculus. Starting from elementary

school to university. M. Hohenwarter created the

software GeoGebra in 2002 for the purpose of

learning and teaching mathematics. Technical

qualities of the software GeoGebra are (Chrysanthou,

2008):

 An open source software (www.geogebra.org).

 Opportunities to change the language (more

than 50 languages), making it suitable for

training of multi-ethnic groups.

 Suitable for use for different age groups at

different stages of training – GeoGebraPrim.

 Possibility to modify the interface level if

necessary.

 Has tools for adding animation, dynamic text;

work online / offline mode

 Compatible with new hardware (GeoGebra

Tablet Apps, iPhone, iPad, Android, Google

Play Apps, Windows 8,10) and software

technologies (GeoGebra Chrom App,

GeoGebra Web Application)

 Maintain installations for widely used

platforms - Windows, Linux, Mac, Ubuntu &

Debian, Fedora, open SUSE, UNIX, and XO -

one laptop per child.

 Ability to share materials and connection with

others in the online space – GeoGebraTube.

 Access the GeoGebra UserForum where one

can discuss their questions and ideas

(Hohenwarter and Preiner, 2007).

GeoGebra also can be used as media mathematics

learning to demonstrate or visualize mathematical

concepts and as a tool to construct concepts

mathematically. An environment of open source tools

around the dynamic mathematics software GeoGebra

where educators can join an online community for

creating and modifying mathlets (Hohenwarter and

ICLI 2018 - 2nd International Conference on Learning Innovation

Preiner, 2007). All materials in this GeoGebra

environment are subject to a Creative Commons

license that allows everyone to make customized

works for non-commercial purposes.

4 PROOF PYTHAGOREAN

THEOREM WITH GEOGEBRA

This proof is the area of the square that built on each

side of a right triangle and animation with translation,

let’s prove it.

a. Construct the right triangle and draw three square

of each side.

Figure 3: Right triangle and three square of each.

Right triangle ABC, the AB side is adjacent, the

AC side is opposite and the BC side is hypotenuse and

draws three square of each side. The ABIH square is

on the AB side (adjacent). The CAGF square is on the

AC side (opposite). The BCED square is on BC side

(hypotenuse).

b. Draw to parallel line then the intersection of that

two line.

Figure 4 : Parallel line in CAGF square.

On the CAGF square draw line then intersection

of that two line and create L point in AG side and K

point AC and J point in the middle the CAGF square

and hide to two line.

c. Draw polygons and make different colour.

Figure 5. Different colour for polygons.

On the square of the AC side draw 4 polygons.

The polygons are FJKC, FJG, GJL, and JKAL. Then

each of the Polygons chose different colour including

the square ABIH.

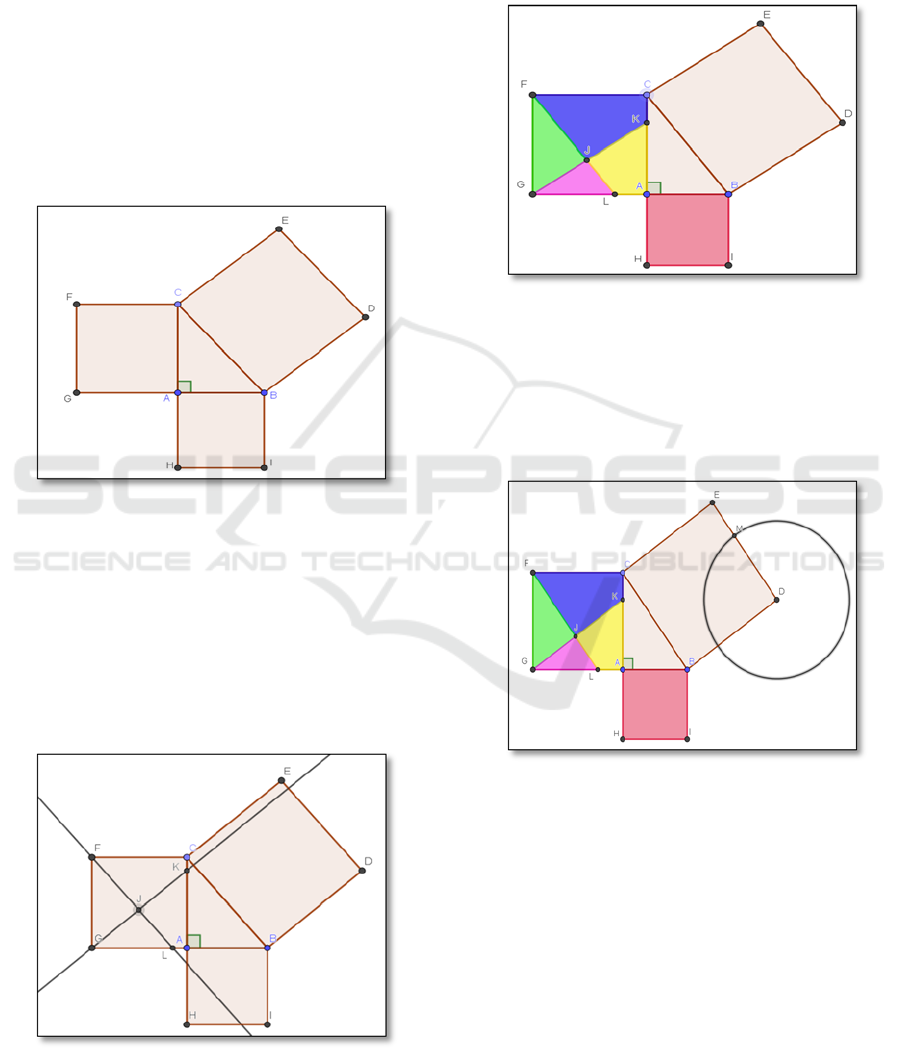
d. Draw circle with center D and radius FJ.

Figure 6: Circle on D point centre.

Chose icon Circle or compass name on toolbox

GeoGebra and draw a circle radius F and J create a

circle move to D point. Then intersect circle create M

point and hide circle line.

e. Create slider input Min = 0, Max = 1, Increment

= 0.01, Speed = 3 and Increasing (Once). On

toolbox chose slider entry Name, Interval, and

Speed.

Using Technology in Mathematics Discover and Proof Pythagorean Theorem with GeoGebra

Figure 7: Slider.

f. Draw vector with input Bar enters every vector

and Translation by vector.

 ua*VectorJ,E

 va*VectorJ,D

 va*VectorJ,B

 tta*VectorJ,C

 rra*VectorB,M



Figure 8: Translation polygon by vector.

Every input bar enters show straight line on the

right. Chose icon Translate by vector on toolbox

GeoGebra and translate polygon by vector until

appearing toward BCED square. Every polygon will

translation toward BCED square.

g. Hide all vector and points after that drag and

slider to see proof Pythagorean Theorem. The

proof with the GeoGebra shows animation

moving the sliders a = 0 to 1.

Figure 9: Proof with the GeoGebra.

The rearrangement two dimension figure the

ABIH square and the CAGF square of the 4 polygons

are FJKC, FJG, GJL, and JKAL then translation to the

hypotenuse side the BCED square. (International

GeoGebra Institute, 2018) Proven to be the sum of the

square and polygon is congruent area on the

hypotenuse side.

5 RESULT AND DISCUSSION

The Pythagorean Theorem has an important role in

mathematics. In school when we learn trigonometric

the Pythagorean Theorem is always used to construct

concepts. Trigonometric concepts and ideas continue

to be an important component of the high school

mathematics curriculum (May and Courtney, 2016).

In the proof, the Pythagorean Theorem is very

diverse. This is approach to prove Pythagoras’s

theorem with GeoGebra.

Figure 10: Area the BCED square.

Area of BCED square = 26.37 where this is the

hypotenuse of the BC side. The hypotenuse is the

long side of a right triangle. AB side is adjacent, area

of ABIH square = 9. Ac side is opposite, area of

FCGL divided by 4 polygons: FCKJ = 7 , JKAL =

4.12 , JLG = 2.13 , FJG = 4.12.

Figure 11: Translation to the BCED square.

ICLI 2018 - 2nd International Conference on Learning Innovation

Sum of ABIH, FCKJ, JKAL, JLG, FJG is equal to

the area of BCED square.

9+7+4.12+2.13+4.12=26.37, The square on the

hypotenuse of a right triangle is equal to the sum of

the squares on the two legs.

This is one of the evidences in proving the truth of

Pythagorean Theorem, with the use of GeoGebra.

Students can explore geometric objects visually and

dynamically to produce their findings. It is the ability

to produce a visualization of the output of geometric

objects quickly and accurately. According

(Contreras, 2014), using Geogebra to guide learners

to discover and extend one of the most beautiful and

elegant theorems. GeoGebra would help students to

explore the concept more in detail and help them to

build and develop their knowledge.

6 CONCLUSION

This paper, I have illustrated how we can use

technology as a learning resource to prove the

Pythagorean Theorem by using GeoGebra programs.

In addition, students and teachers will know the tools

and the function of GeoGebra programs.

Unintentionally it will practice their own skill. I

challenge the readers for knowing GeoGebra program

which can facilitate the readers to learn mathematics

easily. By doing that practice, the readers are

expected for getting a new point of view and

paradigm about the proof Pythagorean Theorem.

REFERENCES

basic-mathematics.com (2016) Pythagorean theorem word

problems. Available at: https://www.basic-

mathematics.com/pythagorean-theorem-word-

problems.html (Accessed: 12 July 2018).

Bogomolny, A. (2016) Pythagorean Theorem. Available at:

http://www.cut-the-knot.org/pythagoras/ (Accessed: 12

July 2018).

Chrysanthou, I. (2008) The use of ICT in primary

mathematics in Cyprus: The case of GeoGebra.

Universitat of Cambridge.

Contreras, J. N. (2014) ‘Discovering and Extending

Viviani’s Theorem with GeoGebra’, GeoGebra

International Journal of Romania, 3(1).

Hohenwarter, M. and Preiner, J. (2007) ‘Creating mathlets

with open source tools’, Journal of Online Mathematics

and its Applications, 7.

International GeoGebra Institute (2018) Pythagorean

Theorem, GeoGebra. Available at:

https://www.geogebra.org/material/show/id/sukabedj

(Accessed: 24 August 2018).

May, V. and Courtney, S. (2016) ‘Developing Meaning in

Trigonometry’, Illinois Mathematics Teacher, 63(1),

pp. 25–33.

National Council of Teachers of Mathematics (2000)

‘Principles and standards for school mathematics’.

National Council of Teachers of.

Parada-Daza, J. R. and Parada-Contzen, M. I. (2014)

‘Pythagoras and the Creation of Knowledge’, Open

Journal of Philosophy, 40(01), pp. 68–74.

Using Technology in Mathematics Discover and Proof Pythagorean Theorem with GeoGebra