
On Trimmed Data Effect in Parameter Estimation of
Some Population Growth Models
Windarto, Eridani and Utami Dyah Purwati
Department of Mathematics, Faculty of Science and Technology, Universitas Airlangga, Surabaya, Indonesia
Kampus C Universitas Airlangga, Mulyorejo, Surabaya 60115, Indonesia
Keywords: Growth Model, Parameter Estimation, Chicken Weight, Trimmed Data.
Abstract: Logistic model, Gompertz model, Richard model, Weibull model and Morgan-Mercer-Flodin model are
commonly used to describe growth model of a population. In this paper, we study the effect of trimmed data
on parameter estimation results of those models. We use chicken weight data cited from literature.
Parameter values of the models from the complete data and the trimmed data are compared. Then, the
sensitivity index of all parameters is evaluated. We found that that sensitivity order of the models from the
highest sensitivity was the Morgan-Mercer-Flodin, Weibull, Richards, logistic and Gompertz growth model.
For practical applications, Gompertz model and Richards are recommended in order to modelling growth of
a population.
1 INTRODUCTION
Mathematical growth models have been widely
applied to explain body weight and age relationship
in veterinary sciences. From the mathematical
growth model, one can evaluate some important and
practical parameters, e.g. the mature weight, the
maturing rate and the growth rate of an animal. The
parameters are beneficial tool to give estimations of
the daily feed needs or to evaluate the effect of
environmental condition on the weight growth of an
animal. In addition, the mathematical growth models
could be applied to forecast the optimum slaughter
age. Therefore, mathematical growth models could
be considered as an optimization instrument for the
animal production (López et al., 2000; Vázquez et
al., 2012; Teleken et al., 2017).
The mathematical growth model could be
classified into two groups, namely empirical growth
models and the empirical growth model and
dynamical growth models (the growth model
derived from ordinary differential equations). The
empirical growth models include Weibull growth
model and MMF (Morgan-Mercer-Flodin) growth
model. The Weibull and the MMF growth model
have been applied to describe chicken growth
dynamic (Topal and Bolukbasi, 2008). The
dynamical growth model includes logistic growth
model, Gompertz growth model, and Richards
growth model. These dynamical growth models have
been used to describe the growth kinetics of many
animals, including chicken (Aggrey, 2002),
mammal (Franco et al., 2011), fish (Santos et al.,
2013), reptile (Bardsley et al., 1995) and
amphibian (Mansano et al., 2013).
Topal and Bolukbasi reported that the MMF,
Weibull and Gompertz the MMF, Weibull and
Gompertz growth model can be useful for describing
chicken growth performance, since these models
were the best fitted models (Topal and Bolukbasi,
2008). Aggrey found that the Richards and
Gompertz growth model have the best fitted model
in explaining rooster and hen growth dynamics
(Aggrey, 2002). Zadeh and Golshani also reported
that the Richards growth model provided the best fit
to the growth curve of Iranian Gulian sheep (Zadeh
and Golshani, 2016).
A mathematical growth model could be said as
a good model if the model give accurately
predicted result and it is robust with trimmed
data. In this context, we compare robustness of
some mathematical growth model due to
trimmed data effect. We use sensitivity index to
measure robustness performance of the models.
We use chicken weight data cited from literature.
This paper is organized as follows. Section 2
briefly presents some mathematical growth models.
Section 3 presents effect of trimmed data on
robustness performance of the selected models.
Finally, conclusions are presented in Section 4.
Windarto, ., Eridani, . and Purwati, U.
On Trimmed Data Effect in Parameter Estimation of Some Population Growth Models.
DOI: 10.5220/0008516300050008
In Proceedings of the International Conference on Mathematics and Islam (ICMIs 2018), pages 5-8
ISBN: 978-989-758-407-7
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
5

2 SOME MATHEMATICAL
GROWTH MODELS
In this section, we briefly present some
mathematical growth models including empirical
growth models and dynamical growth models. Let
represents chicken body weight at time t. The
Weibull and MMF growth model are given by
(1)
and
(2)
respectively. Here, is chicken mature weight,
while are empirical parameters (Topal and
Bolukbasi, 2008).
Logistic growth model is derived from the
following differential equation
(3)
Here is per capita growth rate. The logistic growth
model is analytical solution of Eq. (3), which is
given by (Aggrey, 2002; Windarto et al., 2014)
(4)
where
Here
is the inflection
time, where at chicken growth is maximum at the
inflection time.
The Gompertz growth model is derived from the
following Gompertz differential equation
(5)
The exact solution of Eq. (5) represents the
Gompertz growth model. The Gompertz growth
model is given by
(6)
where
The Richards growth model is derived from the
Richards differential equation
(7)
Here is the shape parameter in the Richards
differential equation. For =1, then the Richards
differential equation could be simplified into logistic
differential equation. Hence, Richards differential
equation could be considered as an extension of the
logistic differential equation. The exact solution of
the Richards differential equation in Eq. (7) is given
by
(8)
where
3 EFFECT OF TRIMMED DATA
ON THE ROBUSTNESS
PERFORMANCE
In this section, we study effect of trimmed data on
robustness performance of the growth models
presented in the previous section. We used rooster
weight data cited from literature (Aggrey, 2002;
Windarto et al., 2014). The rooster weight data
at the day
is presented in the Table 1.
Table : Means of the rooster weight data (y)
t (days)
y (grams)
t
(days)
y (grams)
0
37
42
519.72
3
41.74
45
577.27
6
59.19
48
633.59
9
79.94
51
667.18
12
102.96
54
717.17
15
132.13
57
786.35
18
170.18
71
1069.28
21
206.56
85
1326.49
24
250.71
99
1589.71
27
285.27
113
1859.26
30
324.92
127
2015.44
33
372.83
141
2142.31
36
417.41
155
2220.54
39
469.13
170
2262.63
At the first step, we estimate parameters in the
growth model before trimmed data. We estimate the
parameters such that the mean square error (MSE)
which is given by
, (9)
ICMIs 2018 - International Conference on Mathematics and Islam
6
is minimum. Here,
and
are rooster weight data
and predicted rooster weight at the i-th day, while
is number of observation data.
We used Lavenberg-Marquardt algorithm to find
the optimal parameters for the optimization problem
given in Eq. (9). Estimation results of the Weibull,
MMF, logistic, Gompertz and the Richards growth
model for the rooster weight and the mean squared
error of the models are presented in the Table 2.
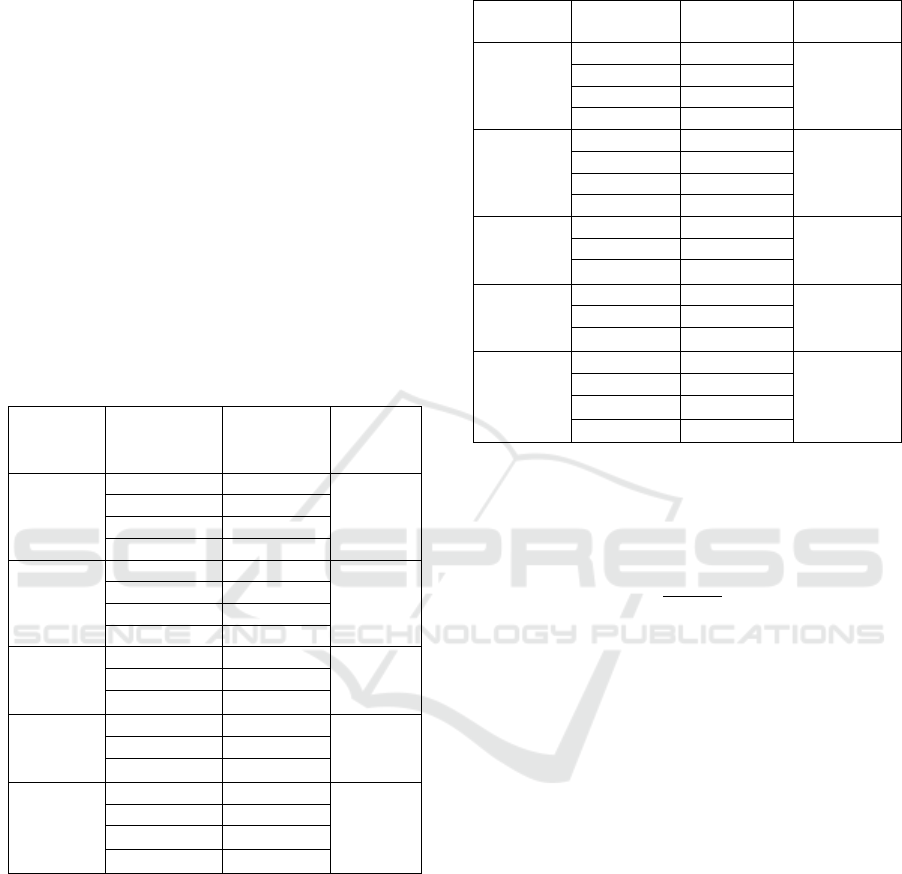
From the Table 2, we found that the Weibull was the
best models, while the logistic growth model was the
worst model. We also obtained that accuracy of the
Weibull model and the Richards model did not
considerably differ. We also found that mean
squared error of the Richards model and the
Gompertz model did not significantly differ. This
was apparently caused by the shape parameter in
the Richards model was almost zero.
Table 2: Estimated parameters value for the whole data
Growth
Model
Parameters
Estimated
value
MSE
Weibull
K
2426.1709
347.743
A
58.2211
B
0.000197
D
1.8699
MMF
A
67.7095
793.779
B
14411.3917
C
2996.0317
D
2.1030
Logistic
K
2279.9041
1887.461
r
0.0403
74.6775
Gompertz
K
2539.6505
384.666
r
0.0220
63.4975
Richards
K
2512.9724
376.277
r*
0.0230
64.3072
0.0541
In order to study the effect of trimmed data, we
also estimated parameters of the models for trimmed
data at the end of the original data (the data from t =
0 until 127 days). We estimated parameters in the
models for the trimmed data. We presented
estimation results for the trimmed data in the Table
3. From the Table 3, we found that the Weibull
model and the MMG model were the best models,
while the logistic growth model was the worst
model. It indicates that the empirical models are
more suit when they are applied in a short data. We
also obtained that accuracy of the Gompertz model
and the Richards model did not considerably differ.
Table 3: Estimated parameters value for the trimmed data
Growth
Model
Parameters
Estimated
value
MSE
Weibull
K
2992.8983
111.903
A
41.9675
B
0.000334
D
1.6772
MMF
A
43.5080
139.359
B
5355.9663
C
4540.7213
D
1.7266
Logistic
K
2132.0511
1708.691
r
0.0433
70.3077
Gompertz
K
2694.6160
230.084
r
0.0206
66.8981
Richards
K
2694.3571
230.053
r*
0.0206
66.8987
0.0002
In order to measure effect of trimmed data on
robustness performance of the models, we defined a
sensitivity index of all parameters in the model. For
any parameter , we defined the sensitivity index as
(10)
Here
is the parameter value after trimmed data
process. Sensitivity index of all parameters was
presented in the Table 4.
From the Table 2 and Table 3, we found that the
mean squared error of the Weibull model and the
MMF model drastically increased due to adding a
few data. From the Table 4, we found that average
value of the sensitivity index varied from 5.94%
until 42.01%. In addition, we found that the shape
parameter in the Richards model was very
sensitive, while the remaining parameters in the
Richards model were robust. Furthermore, we found
that the Gompertz growth model was a robust model
with respect to trimmed data. We also obtained that
sensitivity index of the empirical model were more
sensitive than the dynamical model studied in this
paper. Hence, we found that the empirical growth
model was more sensitive than the dynamical
growth models. For practical applications, Gompertz
model and Richards are recommended in order to
describing a population growth.
On Trimmed Data Effect in Parameter Estimation of Some Population Growth Models
7
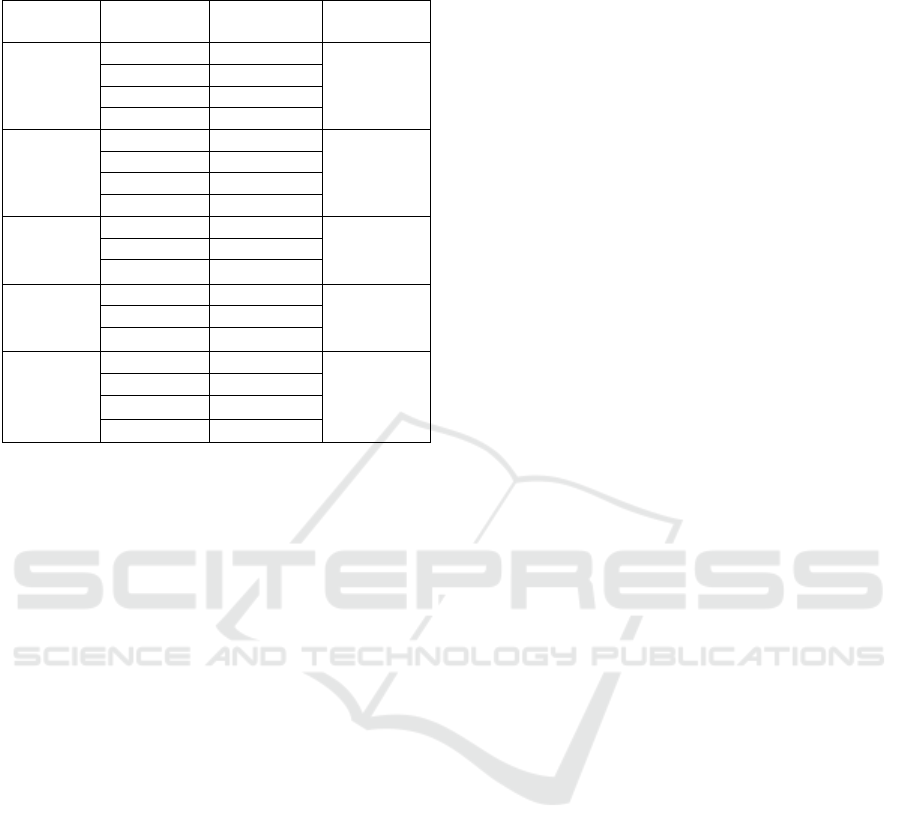
Table 4: Sensitivity index of all parameters.
Growth
Model
Parameters
Sensitivity
index
Average
value
Weibull
K
0.2336
0.3278
A
0.2792
B
0.6954
D
0.1031
MMF
A
0.3574
0.4201
B
0.6284
C
0.5156
D
0.1790
Logistic
K
0.0649
0.0659
R
0.0744
0.0585
Gompertz
K
0.0610
0.0594
R
0.0636
0.0536
Richards
K
0.0722
0.3034
r*
0.1049
0.0403
0.9961
4 CONCLUSIONS
We have studied effect of trimmed data on
parameter estimation results of some empirical
models (Weibull and Morgan-Mercer-Flodin) and
some dynamical models (logistic, Gompertz and
Richards growth model). We found that the
empirical models were more sensitive than the
dynamical models. We also found that the
dynamical models were more robust with respect to
trimmed data. For practical applications, Gompertz
model and Richards are recommended in order to
modeling growth of a population.
ACKNOWLEDGEMENTS
Part of this research was supported by Ministry of
Research, Technology and Higher Education,
Republic of Indonesia through “Penelitian Unggulan
Perguruan Tinggi” research project.
REFERENCES
Aggrey, S. E., 2002. Comparison of three nonlinear and
spline regression models for describing chicken
growth curves. Poultry Science 81(12):1782-1788.
Bardsley, W. G., Ackerman, R. A., Bukhari, N.A.,
Deeming, D.C., Ferguson, M. W., 1995.
Mathematical models for growth in alligator
(Alligator mississippiensis) embryos developing at
different incubation temperatures. Journal of
Anatomy 187(1):181-190.
Franco, D., García, A., Vázquez, J. A., Fernández, M.,
Carril, J.A., Lorenzo, J.M., 2011. Curva de
crecimiento de la raza cerco celta (subrariedad
barcina) a diferentes edades de sacrifício. Actas
Iberoamericanas de Conservacíon Animal 1(1): 259-
263.
López, S., France, J., Gerrits, W. J., Dhanoa, M.S.,
Humphries, D.J., Dikstra, J., 2000. A generalized
Michaelis-Menten equation for analysis of growth.
Journal of Animal Science 78(7): 1816-182.
Mansano, C. F. M., Stéfani, M. V., Pereira, M. M.,
Macente, B. I., 2013. Deposição de nutrientes na
carcaça de girinos de rã-touro. Pesquisa
Agropecuária Brasileira 48(8): 885-891.
Santos, V. B., Mareco, E. A., Silva, M. D. P., 2013. Growth
curves of Nile tilapia (oreochromis niloticus)
strains cultivated at different temperatures. Acta
Scientiarum Animal Sciences 35(3):235-242.
Teleken, J. T., Galvã, A. C., Robazza, W. D. S., 2017.
Comparing non-linear mathematical models to
describe growth of different animals. Acta
Scientiarum 39: 73-81.
Topal, M., Bolukbasi, S. D., 2008. Comparison of
nonlinear growth curve models in broiler chicken.
Journal of Applied Animal Research 34(2):149-152.
Vázquez, J. A., Lorenzo, J. M., Fuciños, P., Franco, D.,
2012. Evaluation of non-linear equations to model
different animal growths with mono and bisigmoid
profiles. Journal of Theoretical Biology 314(7): 95-
105.
Windarto, Indratno, S. W., Nuraini, N., Soewono, E.,
2014. A comparison of binary and continuous genetic
algorithm in parameter estimation of a logistic
growth model. AIP Conference
Proceedings1587:139–142. 2014.
Zadeh, N. G. H, Golshani, M., 2016. Comparison of non-
linear models to describe growth of Iranian Guilan
sheep. Revista Colombiana de Ciencias Pecuarias
29(3):199-209.
ICMIs 2018 - International Conference on Mathematics and Islam
8
