
On Distance Irregularity Strength of Lollipop, Centipede, and
Tadpole Graphs
Kusbudiono, C.H. Pratiwi
and Kristiana Wijaya
Graph, Combinatorics, and Algebra Research Group Department of Mathematics, Faculty of Mathematics and Natural
Sciences Universitas Jember (UNEJ), Jl. Kalimantan 37 Jember, Indonesia 68121
Keywords: Distance Irregular Vertex K-Labelling, Lollipop, Centipede, Tadpole.
Abstract: Let G be a simple graph. A distance irregular vertex k-labelling of a graph G is defined as a labelling
λ:V(G){1,2,…,k} which is every two distinct vertices x,yV(G) have different weights, wt(x)≠wt(y). The
weight of a vertex x in G, denoted by wt(x), is the sum of the labels of all the vertices adjacent to x (distance
1 from x), namely, wt(x)= ∑
yN(x)
λ(y), where N(x) is the set of all the vertices adjacent to x. The minimum k
for which the graph G has a distance irregular vertex k-labelling is called the distance irregularity strength of
G and denoted by dis(G). In this paper, we determine the exact value of the distance irregularity strength of
lollipop, tadpole, and centipede graphs.
1 INTRODUCTION
A graph labelling is a pairing of the vertices or edges
to a label represented by integers (usually) satisfying
a certain condition. Graph labelling was introduced
in 1960s. There are about 2500 papers about graph
labelling (Gallian, 2016).
The concept of distance irregular vertex labelling
of graphs was introduced in (Slamin, 2017). A
distance irregular vertex k-labelling of graphs G is
an assignment of positive integers to vertex set,
so that the weights calculated
at vertices are distinct. The weight of a vertex
under assignment is the sum of the labels of
all vertices adjacent to , that is
where
is a set of all neighbors of vertex . A
distance irregularity strength of G is the minimum
for which the graph G having a distance irregular
vertex -labeling, denoted by
Not all graphs can be labelled with a distance
irregular vertex -labeling. (Slamin, 2017) gave the
following observation.
Observation 1. Let G be a connected graph.
Suppose
. If
, then G has
no distance irregular vertex k-labelling.
Slamin (2017) determined the distance
irregularity strength of complete, path, cycle, and
wheel graph as follows:
forod(8).
Next, (Novindasari et al., 2016) determined the
distance irregularity strength of ladder graph and
triangular ladder graph, that is
.
A lower bound of a distance irregularity strength
can be seen as follows:
Lemma 1. Let G be a connected graph on n
vertices with minimum degree andmaximum
degree . If there is no vertex having identical
neighbors, then
. (Slamin, 2017)
Kusbudiono, ., Pratiwi, C. and Wijaya, K.
On Distance Irregularity Strength of Lollipop, Centipede, and Tadpole Graphs.
DOI: 10.5220/0008519902330235
In Proceedings of the International Conference on Mathematics and Islam (ICMIs 2018), pages 233-235
ISBN: 978-989-758-407-7
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
233
Definition 1.A lollipop graph
is a graph
obtained by joining one vertex of a complete
to a
vertex of degree one of a path
.
So, the lollipop graph
has vertices.
Definition 2.A centipede graph
is a graph
obtained by taking of path P
n
and n copies K
1
and
then joining the ith vertex of P
n
with an edge to
every vertex in the ith copy of K1.
Definition 3.A tadpole graph
is obtained by
joining one vertex of a cycle C
n
to a vertex of degree
one of a path
.
In this paper, we discuss about a distance
irregularity strength of a lollipop
, centipede
and tadpole
, for each natural number n and
especially m = 1.
2 MAIN RESULT
In this section, we determine the exact value of a
distance irregularity strength of a lollipop
.
Theorem 1. Let be a natural number and
be a lollipop graph. Then
Proof. Suppose the vertex set of a lollipop
is
, where
,
, and
, for each
. First, we prove that
.
Suppose
, for each
and . Then,
. By
Observation 1,
for each
and . Hence, the labels of all vertices
,
must be different. So,
.
Next, we show that
. We
define a distance irregular vertex
-labeling
of a lollipop
as follows.
Under the labelling , we obtain the vertex weights
of a lollipop
as follows.
The labelling provide different weights for each
vertex and the largest label is which leads to
. We conclude that
for
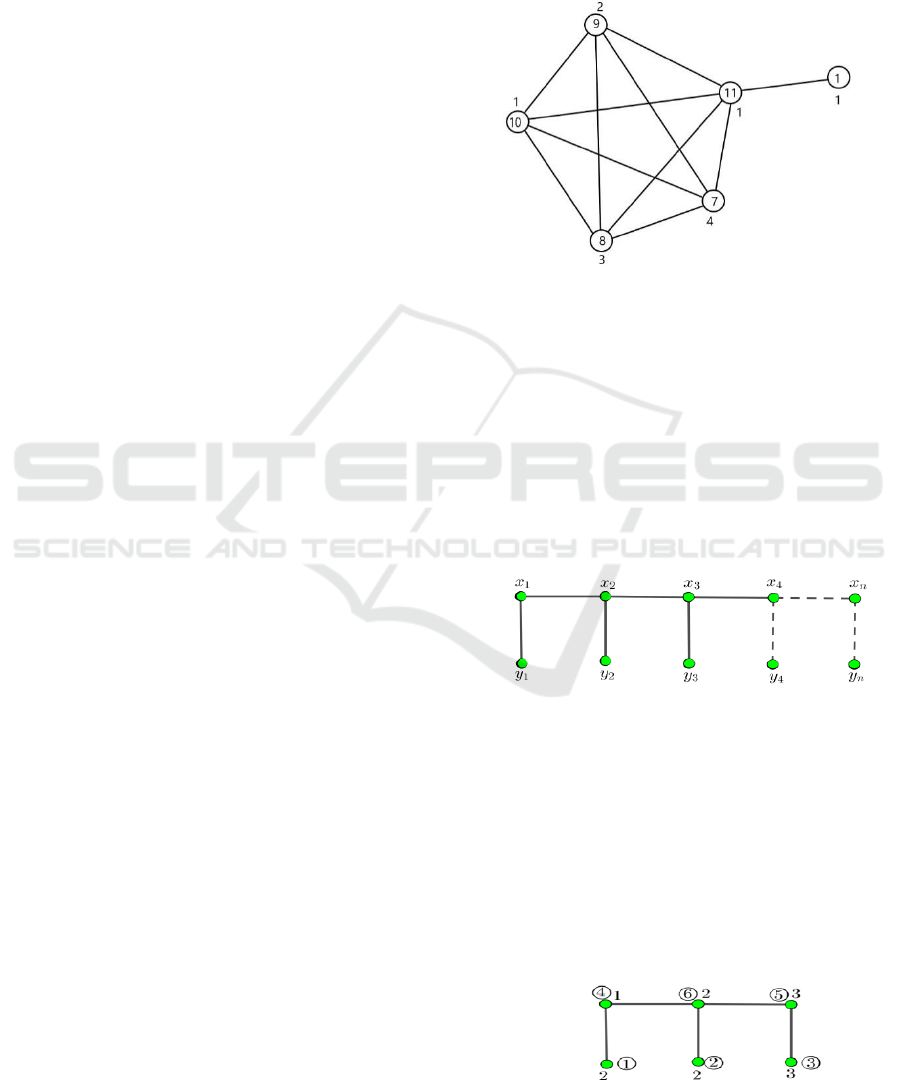
Figure 1 illustrates a distance irregular vertex
labelling of the lollipop graph
with distance
irregularity strength 4. The number in the circle is
vertex weight and number outside the circle is vertex
label.
Figure 1. A distance irregular vertex labelling of
with
dis(
4
Now, we discuss a distance irregularity strength
of a centipede graph
by the following theorem.
Theorem 2. Let
be a centipede graph with
Then
Proof. Suppose
, where
is a leaf for
,
, and
for
and
A vertex notation of centipede
can be seen in
Figure 2.
Figure 2. The notation of vertices in centipede
.
First, we show that
. Since all
leaves
must have distinct weight, label of vertices
must be different for each
. So,
.
Now, we show the upper bound of distance
irregularity strength of centipede. We consider 2
cases.
Case 1. For n = 3.
A distance irregular vertex labeling for centipede
and the weights of its vertices can be depicted in
Figure 3.
Figure 3. A distance irregular vertex labelling of
.
ICMIs 2018 - International Conference on Mathematics and Islam
234

Case 2. For
Define a distance irregular vertex labeling of
centipede
for as follows.
,
Under a labelling , we get the weights of the
vertices of
as follows.
It is clear that every vertex of
has different weight.
This shows that
. Therefore,
.
Slamin (2017) was proved tha
for
. A tadpole
is a graph formed from cycle
by connecting one
vertex to a leaf y. So, we can prove that a tadpole
has a distance irregular vertex k-labelling based
on a distance irregular vertex k-labelling cycle
.
So, we have the following corollary.
Corollary 1. Let
be a tadpole graph with
Then
Proof. (Slamin, 2017) proved that dis(C
n
) =
, for n ≡ 1 mod (4) with the vertex label
:
By connecting a leaf y to the vertex having the
greatest weight x
2
in a cycle C
n
, and giving label of a
leaf is 1, we get
We illustrate distance irregularity vertex
labelling of the tadpole graph in Figure 4.
Figure 4. A distance irregular vertex labelling of
with
dis(
5.
ACKNOWLEDGEMENTS
This research was supported by “Hibah Kelompok
Riset (Graphs, Combinatorics, and Algebra)
Universitas Jember”, Mathematics Department,
Faculty of MIPA, Universitas Jember, No.
2400/STe/UN25.3.1/LT.
REFERENCES
Gallian, J.A., 2016. A dynamic survey of graph labelling.
Electronic Journal of Combinatorics. #DS6.
Novindasari, S., Marjono, and Abusini, S., 2016. On
distance irregular labeling of ladder graph and
triangular ladder graph. Pure mathematical sciences,
Vol. 5(1), pp.75-81.
Slamin, 2017. On distance irregular labelling of graphs.
Far east journal of mathematical sciences (FJMS),
vol. 102(5), pp.919-932.
On Distance Irregularity Strength of Lollipop, Centipede, and Tadpole Graphs
235
