
The Analysis of Students’ Difficulties in
Solving PISA Mathematics Problems
Junaidah Wildani
Prodi Pendidikan Matematika, STKIP Qomaruddin Gresik, East Java, Indonesia
Keywords: Student’s Difficulties, Newman’s Error Analysis, Pisa Problems, Mathematics
Abstract: This study aims to analyse students’ difficulties in solving PISA mathematics problem. The mathematics
tasks for this study was taken from PISA 2012 released mathematics question. For this research, 12 tasks
were selected based on its content area, context, and mathematical process underlying the task. The
participant of this research was 28 students from grade IX Mts Ma’arif Assaadah II Bungah-Gresik. To
collect the data of student’s error, only incorrect or partially correct answer were analysed using Newman’s
error categories namely comprehension, transformation, processing and encoding. The unknown’ category
was added for responses which provide too limited information to be analysed. In total, 201 incorrect and
partially correct answer was gathered from 336 responses. The analysis result shows that 49.3% of error is
located in comprehension, 42.7% in transformation, 7.2% in processing, and only 0.7% error is located in
encoding. Based on mathematical process of the task, students made error the most in employ task. Based
on mathematical content area of the task, students made error the most in change and relationship task. And
the last, based on the context of the task, students made error the most in occupational and scientific task.
1 INTRODUCTION
The Program for International Student Assessment
(PISA) is an international assessment coordinated by
the Organization of Economic Cooperation and
Development (OECD) to measure how well 15
years-old-student prepared to meet their futures
challenges (OECD, 2009; 2013) (OECD,
2009)(OECD, 2013). PISA focuses on the
competencies that indicate students’ capability to
continue learning through their lives by applying the
skill that they acquire in school to non-school
environment, evaluating their choices and making
judgment (OECD, 2013). Hence, beside assessing
students’ knowledge, PISA also assesses students’
capacity to reflect, and to apply their knowledge and
experience in real life. ‘Literacy’ is used as an
umbrella term of these knowledge and skill. PISA
covers three domains: reading, science and
mathematics literacy.
Mathematics literacy in PISA is defined as:
“An individual’s capacity to formulate,
employ and interpret mathematics in a variety
of context. It includes reasoning
mathematically and using mathematical
concepts, procedures, facts and tools to
describe, explain, and predict phenomena. It
assists individuals to recognise the role that
mathematics plays in the world and to make
the well-founded judgments and decisions
needed by constructive, engaged, and
reflective citizen” (OECD2013, p. 25).
The definition above highlights the three phases
of mathematical process; formulate, employ and
interpret. The term ‘formulate’ involves the
capability to transform the presented problem or
situation into mathematical model and recognise
necessary variables and assumptions to solve the
problem. The term ‘employ’ refers to the activities
such as using mathematical reasoning, procedure,
facts, concepts and tools to find the mathematical
solution. As for the term ‘interpret’, it means
interpreting the mathematical solution into the
problem context or situation (OECD, 2013; OECD,
2016).
Based on these mathematical processes, PISA
mathematics problems are classified into three
categories: formulate, employ and interpret. In
addition, PISA mathematics problems are also put
into categories based on its context and content area.
246
Wildani, J.
The Analysis of Students’ Difficulties in Solving PISA Mathematics Problems.
DOI: 10.5220/0008520202460252
In Proceedings of the International Conference on Mathematics and Islam (ICMIs 2018), pages 246-252
ISBN: 978-989-758-407-7
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Based on its context, the mathematics problems are
grouped into four types of problem; personal,
scientific, occupational and societal. As for its
content area, the categories of the problems are
space and shape, quantity, change and relationship,
and uncertainty of data.
PISA results analysis shows that the skill
measured by PISA predicts students’ later success
better than the competencies indicated by students’
academic performance (Schleicher, 2007).
Therefore, many countries including Indonesia use
PISA surveys as reference when they reform their
educational and educational practice (Grek, 2009;
Liang, 2010). Indonesia’s first participation in PISA
was in 2000 (the survey was completed in 2002).
The result was quite shocking as among 41
participating countries, Indonesia ranked in 38
th
place far below Thailand, a neighbourhood country
(OECD, 2004). This result indicates that the
education quality of Indonesia was low by
international standard (The World Bank, 2015). The
result of PISA 2000 evoked Indonesian government
to invest massively for Indonesia’s education system
(The World Bank, 2015).
Despite the huge investment, there was no
significant increase of Indonesian school children’s
performance in the next PISA, especially in
mathematics literacy. In PISA 2012 where
mathematics is the major domain, Indonesian school
children mathematics performance ranked in 64
th
place among 65 participating countries lower then
Malaysia, Thailand and Vietnam (OECD, 2013).
2012 was not the only year Indonesian students
performed poorly in mathematics. In PISA 2009
only one third of Indonesian school children could
solve mathematics task involving daily life context
despite all the information needed to solve the task
was given and the questions was clearly defined
(OECD, 2010).
The poor performance in mathematics literacy by
Indonesian students in PISA should become concern
of Indonesian government and educators as
mathematical problems presented in PISA are
related to everyday life where various contexts are
involved. These problems require students to apply
some fundamental mathematical capabilities such as
communication, mathematising, representation,
reasoning and argument, devising strategies to solve
the problem, using symbolic, formal and technical
language and operations, and using mathematical
tools. These capabilities also become the focus of
newest mathematics curriculum in Indonesia
(namely curriculum 2013) as mentioned in the 3
rd
and 4
th
mathematics core competencies which reflect
the qualities that must be mastered by students when
they finish their education in primary and secondary
level (Kementrian Pendidikan dan Kebudayaan
Republik Indonesia, 2013) stating “understanding,
applying and analysing factual, conceptual, and
procedural knowledge…” and “experimenting,
processing, reasoning, and presenting knowledge in
concrete and abstract domain…”. That being said,
Indonesian students’ constant poor performance in
mathematics domain in PISA may suggest that
school education failed to help students in achieving
those competencies.
Considering the poor performance of Indonesian
students in PISA, especially in mathematics domain,
it is necessary to investigate students’ difficulties in
solving PISA mathematics problem. Hence, this
study aims to analyse students’ difficulties to solve
PISA mathematics problem. Four research questions
are derived from this aim:
1) What errors do students make when solving
mathematics problem from PISA 2012?
2) Based on the mathematical content area, in
what type of task do students make error the
most?
3) Based on the context, in what type of task do
students make error the most?
4) Based on the mathematical process, in what
type of task do students make error the most?
2 METHODS
2.1 Participant
The participants of this study were28 students from
grade IX in MTs Ma’arif Assa’adah II Bungah-
Gresik-Indonesia with the age ranged from 14 to 15
years old (21 students were 14 years old, and 7
students were 15 years old). The selection of the age
range of the subjects aimed to have the subject of
this research close to the age range of PISA target.
The gender of all participants was female as the
school where the data was collected is a junior high
school for girls.
2.2 Instrument
The mathematics problem used for this study was
taken from released mathematics items by PISA
2012. The problems were selected such that each
process, context, and content distributed equally in
the questions given to the participant. In total, 12
questions were selected with each process consists
of four questions, each content consists of three
questions and each context consist of three
questions. The selected questions then translated into
Bahasa Indonesia, and then the researcher consulted
the mathematical questions to experienced teacher to
The Analysis of Students’ Difficulties in Solving PISA Mathematics Problems
247
ensure that the language used in the questions will
be understood by primary school students. Few
adjustments regarding the language were made
according to the suggestion given by the teacher.
The participants were asked to solve these questions
in 90 minutes. In this research, the term
‘mathematical task’ will be used instead of
‘mathematical question’.
2.3 Data Analysis
To analyse students’ error, only the incorrect and
partially correct responses were analysed. The
incorrect responses were coded based on Newman’s
error categories. Newman (Newman, 1977)
developed a model to classify the error student
makes during problem solving. He proposed five
types of error: error of reading, comprehension,
transformation, process skill and encoding. The table
1 explain each type of error.
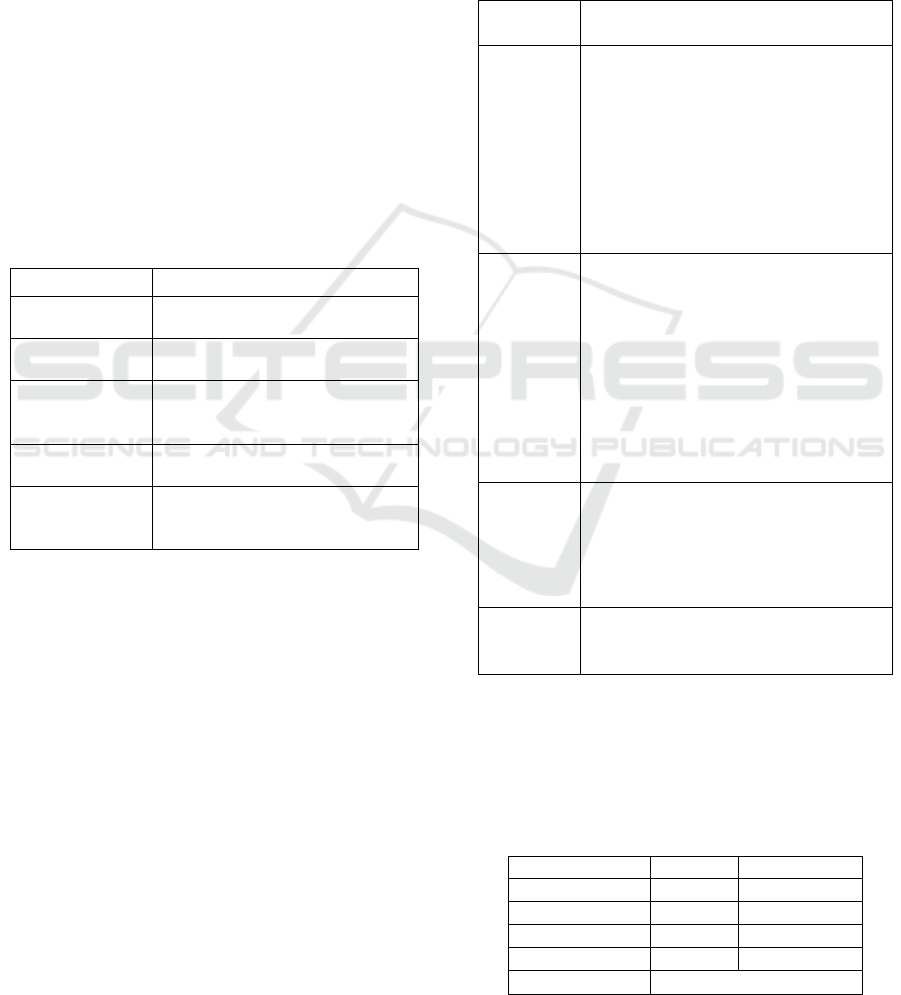
Table1: Description of Newman’s error analysis.
Type of error
Explanation
Error of reading
Error in simple recognition of
words and symbols
Comprehension
Error in understanding the
meaning of the problem
Transformation
Error in transforming a word
problem into appropriate
mathematical problem
Process skill
Error in performing mathematical
procedure
Encoding
Error in presenting the
mathematical solution into
acceptable written form
In this study, the reading error from Newman’s
error categories was left out because this type of
error doesn’t indicate the difficulty/incapability to
understand the meaning of the problem (Wijaya, et
al., 2014). In addition, ‘unknown’ was added to error
categories for responses which provide too limited
information or no information at all to be analysed.
The coding scheme used to analyse the error was
adapted from ‘Coding Scheme for error types when
solving context-based mathematics tasks’ (Wijaya,
et al., 2014). The adaptation was conducted by
adjusting the explanation of each type of error based
on the nature of mathematical task used in this study
and the error found during the analysis (table 2).
3 RESULTS AND DISCUSSION
In total, 201 (59.8%) incorrect and partially correct
answers were gathered from 336 responses. Among
these 201 answers, 74 answers couldn’t be analysed
as the answer didn’t provide any information or the
information was too limited which left 127 answers
to be analysed.
Table 2: Coding scheme for error analysis.
Type of
error
Explanation
Compre-
hension
- Incorrect interpretation of the
instruction
- Misunderstood a keyword(s) which is
usually mathematical term
- Unable to select relevant information
from the task
- Unable to gather information which
is not provided explicitly in the task
- Use the irrelevant information from
the task to solve the problem
Transform
ation
- Use mathematical
procedure/formula/algorithm directly
without analysis if it is necessary for
the task
- The answer only refers to the context
or real-world setting without
considering the mathematics
perspective
- Use incorrect mathematical
procedure/concept/fact/algorithm
which is not relevant to the task
Process
skill
- Error in solving algebraic expression
or function
- Error in calculation
- Incorrectly use the measurement
- Use the correct formula/procedure
but unable to finish the calculation
Encoding
The answer does not reflect to the
context which is indicated by
unrealistic answer
The analysis result of the incorrect and partially
correct answer about the error that students made
when solving PISA mathematics problem can be
seen in the table 3.
Table 3: Distribution of error
Type of error
n
Percentage
Comprehension
68
49,3%
Transformation
59
42,7%
Process skill
10
7,2%
Encoding
1
0,7%
Total
138
ICMIs 2018 - International Conference on Mathematics and Islam
248

The total number of errors exceeds the number of
analysed answer because multiple codes was applied
where it was possible there were more than one type
of error in one answer.
The table shows that according to Newman’s
error analysis result, the most common error
occurred was comprehension error followed by
transformation error. This implies that the most
difficult stage in solving PISA mathematics problem
for students is in understanding the meaning of the
problem and transforming the word problem into
appropriate mathematical model. The figure 1 is the
example of students work and the error they made.
Figure 1: Student’s work where she made comprehension
error.
In this work, student failed to select relevant
information from the task showing that there is 152
MB space in Ivan’s memory stick which leads to the
wrong answer. This type of error is included in
comprehension error.
Figure 2: Student’s work where she made transformation
error.
Figure 2 above shows that student was unable to
perform the correct mathematical procedure where
she should have divided the difference by the weight
of the first egg and then multiplied it by 100% to get
the correct percentage. Instead, she directly put “%”
in her answer which results the wrong answer. This
error is included in transformation error category.
Figure 3: Student’s work where she made process skill
error.
English translation:
Answer: NO
Because by deleting two albums, for example 100+
75 MB will only result 175 MB free space whereas
Ivan needs to transfer 350 MB album. Hence,
deleting two albums will not give Ivan enough space
The Analysis of Students’ Difficulties in Solving PISA Mathematics Problems
249

In this task, student was able to perform the
correct mathematical procedure, but she was unable
to finish the calculation which results in unfinished
answer. The inability to finish the calculation is
included in process skill error.
Figure 4: Student’s work where she made encoding error.
The picture 4 shows the solution for the same
mathematical task indicated in Fig. 3 where students
were asked to calculate the length of the rope. She
answered that the length of rope is 45
o
. The error in
this answer is the use of the unit system for length.
She used degree instead of meter. The response of
student indicated in Fig. 4 shows that students gave
unrealistic answer within the context of this task.
Hence, this error is included in encoding error.
The type of error in Neman’s error category
reflects the stages in answering mathematics word
problem (Newman, 1977). If the type of error in
Newman classification is viewed as stages, then
comprehension and transformation are included in
earlier stages of problem solving. This suggests that
students already faced the difficulties in the earlier
stage of solving PISA mathematics problem when
they had to understand the meaning of the problem
and transform the word problem into appropriate
mathematical model.
Distribution of incorrect and partially correct
answer in mathematics task based on its content
area, context and mathematical process can be seen
in the table 4. The table 4 indicates that among four
types of mathematics task based on its content area,
students had most difficulties in the problems which
content area is change and relationship. This type of
problem requires student to understand about
various types of changes and know their occurrence
so that students can use appropriate mathematical
models to describe and predict the change (OECD,
2013). Being less literate in this area implies that
students lack understanding about these knowledge.
Furthermore, it also implies students lack skill in
mathematics modelling and representation which are
important aspect of change and relationship.
Table 4: Distribution of error based on content area,
context, and mathematical process.
Type of task
n (in %)
Correct
Partially
correct
Incorrect
1. Based on its content area
Change and
relationship
10.7
3.6
85.7
Space and shape
42.9
4.8
52.4
Quantity
45.2
0
54.8
Uncertainty and
data
61.9
20.2
17.9
2. Based on its context
Personal
39.3
3.6
57.1
Societal
77.4
0
22.6
Occupational
16.6
25
58.3
Scientific
27.4
0
72.6
3. Based on its mathematical process
Formulate
34.8
17.8
47.3
Employ
24.1
3.6
72.3
Interpret
61.6
0
38.4
The second types of task with huge percentage of
error are quantity task. To solve this type of task,
students must understand about units, magnitudes,
count, measurements and numerical trend and
pattern. Students also must use numerical reasoning
which is the essence of mathematical literacy
relative to quantity (OECD, 2013). Having
difficulties in this area suggest the lack of skill in
number sense, mental calculation, multiple
representation of numbers, estimation and
assessment of reasonableness of result and elegance
of computation as the aspects of quantitative
reasoning as well as lack of understanding about
units, magnitudes, count, measurements and
numerical trend and pattern.
For the type of mathematics task based on its
context, students found it most difficult when
dealing with occupational and scientific problems.
The problem context itself is the students’ world
aspect in which the problems are situated (OECD,
2013). Usually the context of the problem
determines how the problem solver chose their
strategies and representation (OECD, 2016). In
PISA 2012 (which items were used for this study),
occupational context problems encompass the
problems centred around the world of work.
As for scientific problems, it covers the problems
relate to the use or application of mathematics to the
natural world and issues related to science and
technology. The huge numbers of students having
ICMIs 2018 - International Conference on Mathematics and Islam
250

difficulties in these contexts suggest the
unfamiliarity with these kinds of problems which
lead to the possibilities that students were rarely
exposed to problems related to work and science.
For type of mathematics task based on its
mathematical process, students encountered most
difficulties when solving employ problems. The
term ‘employ’ refers to the ability to apply
mathematical reasoning, procedures, fact, and
concept to solve problems formulated
mathematically. It covers some activities such as
devising and implementing strategies to find
mathematical solution, manipulating numbers, data,
and algebraic expressions, and making
generalization (OECD, 2016). The difficulties in the
employing process indicate the lack of mentioned
abilities above.
4 CONCLUSIONS
This study aimed to get better insight about students’
difficulties while solving PISA problems, focusing
on the type of error, mathematical process, content
area, and the context.
The result of this study shows that the most
common difficulties encountered by the students in
solving PISA mathematics problem was
comprehension which is the difficulty in
understanding the meaning of the problem. Students
also had major difficulty in transforming word
problem into mathematical model. On the other
hand, students only made minor error in processing
the mathematical procedure and presenting it in
formal form.
The other finding of this study shows based on
the content area of the problem, students made error
the most when solving change and relationship
problem. Based on the context of the problem,
students found it most difficult to solve occupational
and scientific problem. Meanwhile, based on
mathematical process underlying the mathematical
problem, students had the most difficulties in
problem which mathematical process is ‘employ’.
The result of this study can be used as a basis for
future studies or designing an intervention to solve
educational problem, especially in mathematics
education field
For instance, considering the fact that the most
difficulties encountered by students in solving PISA
mathematics problems is in comprehension and
transformation phase, the future study can be
focused on the efforts of how to improve students’
comprehension and transformation skill. It should be
also noted that reading comprehension has a positive
correlation to student’s mathematics and science
performance in PISA (Akbaşlı, et al., 2016).
In English department, student’s reading
comprehension can be improved using text structure
task (Rohman, 2017). Text structure refers to how
ideas in text are interconnected to deliver message to
reader (Meyer & Rice, 1984). Mathematics teachers
may adapt this strategy into mathematics classroom
to enhance students understanding of mathematics
problem. For future study, mathematics education
researchers may also investigate the effect of these
strategies in students’ mathematics literacy.
Transformation skill is closely linked to
mathematics modelling. Hence, to improve students’
ability in transforming word problem into
mathematics problem, teachers may need to engage
and familiarize students with mathematics modelling
activities. In fact, modelling activities within
classroom has been proven to be effective to
improve students’ mathematical representation
(Hanifah, 2015) which is important aspect of
transformation skill.
The data about the error students made based on
problem’s content area, context and mathematical
process especially provide a basis to design a
learning material (such as students worksheet,
handbook or learning module) to develop or improve
students’ mathematics literacy.
Finally, some limitation of this study should be
considered when readers want to make use of this
study as this study evidently has some limitations.
For example, the finding from the students in this
study does not automatically apply to students in
other school or region. Given the same PISA
questions, the result may differ in the distribution of
error types. The other limitation is in mathematical
task selection. In this study, only 12 tasks were
chosen from 100 tasks in total. If more mathematical
task were used to collect data, there is a possibility
that this study would give different result.
REFERENCES
Akbaşlı, S., Şahin, M. & Yaykiran, Z., 2016. The Effect of
Reading Comprehension on the Performance in
Science and Mathematics. Journal of Education and
Practice, 7(16), pp. 108-121.
Grek, S., 2009. Governing by numbers: the PISA 'effect' in
Europe. Journal of Education Policy, 21(1), pp. 23-37.
Hanifah, 2015. Penerapan Pembelajaran Model Eliciting
Activities (MEA) dengan Pendekatan Saintifik untuk
Meningkatkan Kemampuan Representasi Matematis
The Analysis of Students’ Difficulties in Solving PISA Mathematics Problems
251

Siswa. Kreano Jurnal Matematika Kreatif-Inovatif,
6(2), pp. 191-198.
Kementrian Pendidikan dan Kebudayaan Republik
Indonesia, 2013. Kompetensi Dasar. Sekolah
Menengah Pertama (SMP)/Madrasah Tsanawiyah
(MTs), s.l.: Kementrian Pendidikan dan Kebudayaan
Republik Indonesia.
Liang, X., 2010. Assessment use, self-efficacy and
mathematics achievement: Comparative analysis of
PISA 2003. Data of Finland, Canada and the USA.
Evaluation & Reasearch in Education, 23(3), pp. 213-
229.
Meyer, B. & Rice, G., 1984. The Structure of Text. In P.D
Pearson ed. New York: Longman.
Newman, M. A., 1977. An anlysis of sixth-grade pupils'
errors on written mathematical task. Victorian Institute
for Educational Research Bulletin, Vol. 31, pp. 31-43.
OECD, 2004. Learning for tomorrows' world: First
results from PISA 2003, Paris: OECD Publishing.
OECD, 2009. PISA 2009 Assessment framework: Key
competencies in reading, mathematics, and science,
Paris: OECD Publishing.
OECD, 2010. PISA 2009 results: What students know and
can do. Students' performance in reading,
mathematics, and science (Vol. I), Paris: OECD
Publishing .
OECD, 2013. PISA 2012 Assessment and analytical
framwork: Mathematics, reading, science, problem
solving and financial literacy, Paris: OECD
Publishing.
OECD, 2016. PISA 2015 Assessment and analytical
framework: Science, reading, mathematics and
financial literacy, Paris: OECD Publishing.
Rohman, A., 2017. Improving Students' Comprehension
Through Text Structure Task. Journal of Linguistic
and English Teaching , 2(1), pp. 1-12.
Schleicher, A., 2007. Can competencies assessed by PISA
be considered school knowledge 15-years-old should
possess?. Educational Change, 8(4), pp. 349-357.
The World Bank, 2015. Indonesia: Teacher certification
and beyond. An empirical evaluation of the teacher
certification program and education quality
improvements in Indonesia, Jakarta: The World Bank.
Wijaya, A., Heuvel-Panhuizen, M. v. d. & Robitzch, M.
D. A., 2014. Difficulties in solving context-based
PISA matehmatics task: An analysis of students' error.
The Mathematics Enthusiast, 11(3), pp. 555-584.
ICMIs 2018 - International Conference on Mathematics and Islam
252
