Optimal Control of an HIV Model with Condom Education and
Therapy
Marsudi, Noor Hidayat and Ratno Bagus Edy Wibowo
1
1
University of Brawijaya, Malang, East Java, Indonesia
Department of Mathematics, University of Brawijaya, Malang, Indonesia
Keywords: Human Immunodeficiency Virus (HIV), Optimal Control, Condom Education, Antiretroviral Therapy,
Pontryagin’s Maximum Principle
Abstract: In this paper, we propose and analyze an optimal control problem to asses the effectiveness of control
measures on the spread of HIV. We formulate and analyze a deterministic mathematical model with use of
condom education and antiretroviral therapy as control variables using optimal control theory and
Pontryagin’s maximal principle. We formulated the appropriate optimal control problem and investigate the
necessary conditions for the disease control in order to determine the role of asymptomatic infectives, pre-
AIDS, and full-down AIDS in the spread of HIV. We further investigate the impact of combinations of the
strategies in the control of HIV infection. The combination of antiretroviral therapy on pre-AIDS and full-
blown AIDS shows a significant difference in the number of the infected individuals in the asymptomatic
stage, infected individuals in the pre-AIDS class, and infected individuals in full-blown AIDS class.
1 INTRODUCTION
The model to be considered in this paper is an
extension of the model proposed by Marsudi et. al.
(2017) in which the effect of antiretroviral therapy at
full-blown AIDS group is considered by the inclusion
of model validation and applying optimal control
theory to study and analyze the dynamics of HIV
model. The stability analysis and optimal control of
an epidemic model with vaccination and treatment
have discussed by Sharma and Samanta (2015).
Marsudi et. al. (2018) used the optimal control to
examine the role of educational campaigns and
antiretroviral therapy in controlling the spread of HIV
dynamics. Okosun et. al. (2013) studied the impact of
treatment of HIV/AIDS and screening of unaware
infectives on optimal control of HIV/AIDS.
Many mathematical models of HIV/AIDS
transmission dynamics have been developed
including those with optimal control (Joshi, 2002;
Lenhart and Workman, 2002; Marsudi et. al., 2017;
Yusuf and Benyah, 2011). The main objective of this
paper is to develop a mathematical model for human
interaction, this will be done with the aim of using
three optimal control strategies: condom education,
antiretroviral therapy for pre-AIDS and full-blown
AIDS at different rates on the spread of the disease.
In section 2, we show the mathematical model for
the HIV model that will be studied in this paper.
Sections 3 is presented to the optimal control problem
formulation. In this section, we use Pontryagin’s
maximum principle to analyze the control strategies
and to determine the necessary conditions for the
optimal control of the HIV infection. In Section 4, we
presented the numerical simulations of the model in
order to interpret the results of the dynamics and the
conclusion is presented in Section
2 MATHEMATICAL MODEL
Following the model proposed by Marsudi et. al.
(2017), the total population (N) is divided into six
categories: susceptible (S), susceptible who receive
condom education (E), infected in the asymptomatic
stage (I), infected in pre-AIDS class (P), full-blown
AIDS class (A), and pre-AIDS and full-blown AIDS
who receive antiretroviral therapy (T).
The model is built according to the following
main assumptions:
(i) The rate of transmission is directly proportional to
the susceptibles individuals and also to the ratio
Marsudi, ., Hidayat, N. and Wibowo, R.
Optimal Control of an HIV Model with Condom Education and Therapy.
DOI: 10.5220/0008522804150419
In Proceedings of the International Conference on Mathematics and Islam (ICMIs 2018), pages 415-419
ISBN: 978-989-758-407-7
Copyright
c
 2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
415

between the members of the infected population
(I and P) to the total population.
(ii) Asymptomatic infectives and pre-AIDS class can
infect susceptibles class at different rates
21
and

respectively where
).
21


(iii) Susceptible individuals who receive
condom educations at the rate
1
u
)10(
1
 u
.
(iv) Only pre-AIDS and full blown AIDS can be
treated with antiretroviral therapy at different
rates
2
u
and
3
u
respectively
)3,2,10( = iu
i
.
(v) Asymptomatic infectives only move to pre-AIDS
at different rates
1

and pre-AIDS class will
move to full-blown AIDS at different rates
2

.
(vi) Natural death rate

, the death rate due to full-
blown AIDS and pre-AIDS who receive
antiretroviral therapy at different rates
1

and
2

respectively
).(
21


(vii) The recruitment rate

and condom education
efficacy on the S class is
).10( 

The population is homogeneously mixed and each
susceptible individual has an equal chance of
acquiring HIV infection when contacting
asymptomatic infective individuals or pre-AIDS
individuals.
The population dynamics is given by the
following set of ordinary differential equations:
AμuαPσ
dt
dA
TμAuPu
dt
dT
PμuσIσ
dt
dP
Iμσ
N
EPI
N
SPI
dt
dI
μE
N
EPI
Su
dt
dE
Sμu
N
SPI
Λ
dt
dS
)(
)(
)(
)(
)(
)(
++−=
+−+=
++−=
+−
+−
+
+
=
−
+−
−=
+−
+
−=
312
232
221
1
2121
21
1
1
21
)(1)(
)(1
)(
)(




(1)
with initial conditions
.)0(,)0(
,)0(,)0(,)0(,)0(
00
0000
AATT
PPIIEESS
==
====
(2)
The effective reproduction number
e
R
, for
system (1) is given
( )
.
))()((
])1[(
))((
)1(
2211
112
11
11




++++
+−
+
++
+−
=
uu
u
u
u
R
e
(3)
3 OPTIMAL CONTROL PROBLEM
We search the optimal strategies for implementing
condom education and antiretroviral therapy use on a
finite time
.T
Our goal is to minimize the number of
cases in asymptomatic class I, pre-AIDS class P, full-
blown AIDS class, and the costs required to control
HIV by these three control measures. The objective
function considered takes the form
dtuwuwuwAbPbIbuuuJ
T

++++++=
0
2
33
2
22
2
11
2
1
321321
)]([),,(
(4)
where T stands for the final time to control HIV. The
constants
3,2,1, =iw
i
are measure of the relative
cost of the interventions associated with the control
, and,,
321
uuu
respectively, and the constant
3,2,1, =ib
i
are the weight constant for the class I, P,
and A.
We seek an optimal control triple
) ,,(
*
3
*
2
*
1
uuu
such that
 
UuuuuuuJuuuJ =
321321
*
3
*
2
*
1
,,),,(min),,(
(5)
where
 
],0[,3,2,1,10),,(
321
TtiuuuuU
i
==
is
the control set.
The optimal control must satisfy the necessary
conditions that are formulated by Pontryagin’s
maximum principle7]. This principle transforms the
system of equations (1) and (4) into the problem of
minimizing point-wise a Hamiltonian (H), with
respect to
)(),(),(
321
tututu
as
   
 
.)(
)()(
)(
))(1()(
))(1(
)(
)(
3126
23252214
1
2121
3
21
12
1
21
1
2
33
2
22
2
11
2
1
321
AuP
TAuPuPuI
I
N
EPI
N
SPI
E
N
EPI
Su
SSu
N
SPI
uwuwuwAbPbIbH











++−+
+−++++−+






+−
+−
+
+
+






−
+−
−+






−−
+
−+
+++++=
(6)
where
6,5,4,3,2,1, =i
i

are the adjoint variables
associated by
.,,,,, ATPIES
We differentiate
Hamiltonian (6) with respect to states
,,,,,, ATPIES and
respectively, and then the
adjoint system can be written as
ICMIs 2018 - International Conference on Mathematics and Islam
416

μλuλλ
N
EPβIβ
λλ
N
SPβIβ
N
PβIβ
λλ
S
H
dt
dλ
1121
2
21
23
2
2121
31
1
1
+−+






+−
−+



+
−



+
−=


−=
)(
))((
)(
)(
)(

(7)
μ λ
N
SPβIβ
λλ
N
EPβIβ
N
PβIβ
λλ
E
H
dt
dλ
2
2
21
13
2
2121
32
2
11
+






+
−+



+−
−



+−
−=


−=
)(
)(
))(())((
)(

(8)


3143
2
211
32
2
211
311
3
11
λσλλ
N
EPβIβ
N
Eβ
λλ
N
SPβIβ
N
Sβ
λλb
I
H
dt
dλ
+−+



+−
−



−
−+



+
−



−+−=


−=
)(
))(()(
)(
)(
)(
(9)
μλuλλ σλλ
N
EPβIβ
N
Eβ
λλ
N
SPβIβ
N
Sβ
λλb
P
H
dt
dλ
4254264
2
212
32
2
212
312
4
11
−−−+



+−
−



−
−+



+
−



−+−=


−=
)()(
))(()(
)(
)(
)(

(10)
)
1
5
2
21
23
2
21
13
5
μλ
N
EPβIβ
λλ
N
SPβIβ
λλ
T
H
dt
dλ
++






+−
−+






+
−=


−=
2
(
))((
)(
)(
)(


(11)
.μαλ
uλλ
N
EPβIβ
λλ
N
SPβIβ
λλb
A
H
dt
dλ
)(
)(
))((
)(
)(
)(
++
−+






+−
−+






+
−+−=


−=
16
356
2
21
23
2
21
133
6
1

(12)
The optimal control pair
) ,,(
*
3
*
2
*
1
uuu
that solves
the control problem is the pair of the time-dependent
functions that minimizes H. We solved the equation
0=


i
u
H
at
3,2,1,
*
=iu
i
for
and obtained:
..
3
*
56
3
2
*
54
2
1
*
21
1
w
Aλλ
u
w
Pλλ
u
w
Sλλ
u
c
c
c
)(
)(
)(
−
=
−
=
−
=
(13)
We can now impose the bounds
,3,2,10 = iu
i
on the controls to get
( ) 
( ) 
( ) 
.1,,0
,1,,0
,1,,0
3
*
3
2
*
2
1
*
1
c
c
c
uu
uu
uu
minmax
minmax
minmax
=
=
=
(14)
and
.0,0,0
3
2
3
2
2
2
2
2
1
2
1
2
=


=


=


w
u
H
w
u
H
w
u
H
(15)
4 NUMERICAL RESULTS
In this section, we give some numerical results of the
system (1), using parameter values from Marsudi et.
al. (2018b),
.0139.0
,4621.0,198.0,3.0,0667.0
,0909.0,711.0,1422.0,33638
212
121
=
====
====



and
(16)
and initial conditions
.89)0(,996)0(,34)0(
,67)0(,959)0(,957263)0(
===
===
ATP
IES
(17)
The solution of the optimal control problem was
obtained by solving the optimality system of state and
adjoint system through Forward-Backward Sweep
method Lenhart and Workman (2002). The adjoint
system (7-12) were solved by fourth–order Runge-
Kutta scheme using the forward solution of the state
equations. We used the weight at the final time,
220,50,1
321321
====== wwwbbb and
for
simulation of HIV model with optimal control.
4.1 Strategy A: Control with Combination
of Antiretroviral Therapy of Pre-
AIDS and Full-blown AIDS
In this strategy, we applied antiretroviral therapy
control
2
u
and antiretroviral therapy control
3
u
are
used to optimize the objective function while we set
condom education is set to zero. In Figure 1(a), (b),
and (c), we observe the control strategies with
combination of antiretroviral therapy of Pre-AIDS
and full-blown AIDS results in decreasing the
numbers of infected in the asymptomatic stage I,
infected in pre-AIDS P, and infected in full-blown
AIDS respectively, but not go to zero. Therefore, this
strategy is not 100% effective in eradicating the
disease in the specified period of time.
Optimal Control of an HIV Model with Condom Education and Therapy
417

Figure 1: Simulation optimal control with antiretroviral
therapy on pre-AIDS class and full-blown AIDS group
Figure 1(d) shows the controll profile for
antiretroviral therapy of pre-AIDS class (
2
u
) is at the
upper bound for about
11.8=t
before dropping to
lower bound while the control profile for
antiretroviral therapy of full-blown AIDS (
3
u
) is at
the upper bound until about
59.9=t
before gradually
decreasing to lower bound.
4.2 Strategy B: Control with Combination
of Condom Education and
Antiretroviral Therapy of Full-blown
AIDS
Figure 2 show the simulation of the model where both
control condom education (
1
u
) in susceptible and the
antiretroviral therapy of full-blown AIDS group (
3
u
)
are optimized. The numerical results shows that the
infected individuals in the asymptomatic stage and
infected individuals in pre-AIDS class increases
(Figure 2(a) and 2(b)) while infected individuals in
full-blown AIDS group decrease and then starts to
increase because of a lack of antiretroviral therapy
(Figure 2(c)). As a result, the use combination of
condom education and antiretroviral therapy might
not be sufficient to eradicate the burden of the
infection of HIV.
Figure 2: Simulation optimal control with condom
education on susceptible and full-blown AIDS
Figure 2(d) shows the control profile of
antiretroviral therapy (
3
u
) in which the control
3
u
as
at the upper bound for about
95.9=t
before
dropping to the lower bound at the final time while
the control profile of condom education at the lower
bound from the beginning to the end of the
intervention.
4.3 Strategy C: Control with
Combination of Condom Education
and Antiretroviral Therapy of Pre-
AIDS
With this strategy, the condom education and
antiretroviral therapy are used to optimize the
objective function while controlling antiretroviral
therapy of full-blown AIDS class is set to zero. In
Figure 3(a)-(c) we observe that this control strategy
show a significant decrease in the number of the
infected individuals in the asymptomatic stage,
infected individuals in the pre-AIDS class, and
infected individuals in full-blown AIDS group
compared with the case without control.
The control profile is shown in Fig. 3(d), control
antiretroviral therapy of full-blown AIDS group (
3
u
)
is at the upper bound for about
33.8=t
before
dropping to lower bound while control condom
education (
1
u
) to be at the lower bound.
Figure 3: Simulation optimal control with condom
education and pre-AIDS class.
4.4 Strategy D: Control with Combination
of Condom Education, Antiretroviral
Therapy of Pre-AIDS, and Full-
blown AIDS
In this strategy, the combination of three controls
condom education, antiretroviral therapy of pre-
ICMIs 2018 - International Conference on Mathematics and Islam
418

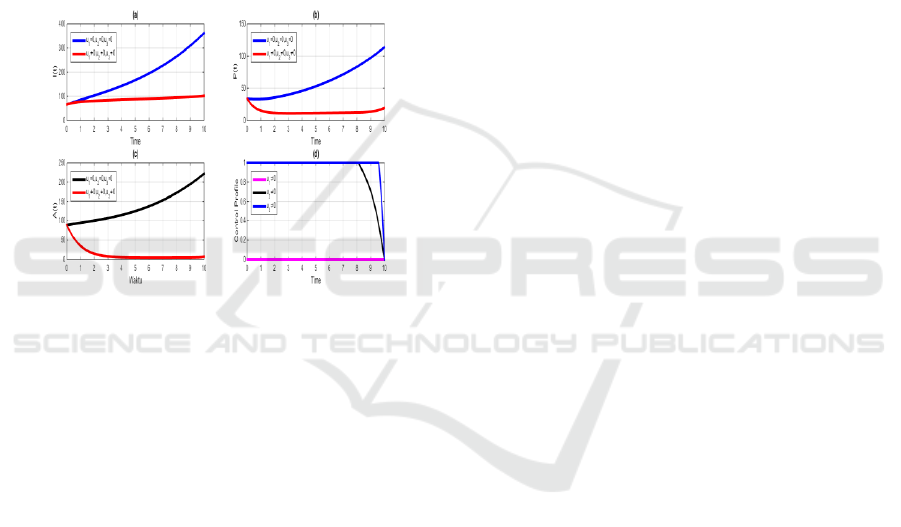
AIDS and full-blown AIDS are used to optimize the
objective function and then analysed its impact in
infected individuals. Figure 4(a)-(c) shows the impact
of with and without control application in the model.
The significant difference is observed in the number
of the infected individuals in the asymptomatic stage,
infected individuals in the pre-AIDS class, and
infected individuals in full-blown AIDS group.
Figure 4(d) showns the the controll profile for
antiretroviral therapy of pre-AIDS class (
2
u
) is at the
upper bound for about
11.8=t
before dropping to
lower bound while the control profile for
antiretroviral therapy of full-blown AIDS (
3
u
) is at
the upper bound until about
59.9=t
before gradually
decreasing to lower bound.
Figure 4: Simulation optimal control with condom
education, antiretroviral therapy on pre-AIDS and full-
blown AIDS
5 CONCLUSIONS
In this paper, a deterministic model with optimal
control for HIV was derived and analyzed to examine
the effect of condom education, antiretroviral therapy
on pre-AIDS and full-blown AIDS on the dynamics
of HIV. The Pontryagin’s maximum principle used to
derive and analyze the necessary conditions for
optimal control strategies such as condom education
(
1
u
), antiretroviral therapy on pre-AIDS (
2
u
), and
antiretroviral therapy on full-blown AIDS (
1
u
) for
minimizing the spread of HIV. Numerically, the
model was analyzed. Graphically, strategies A, C, and
D shows a significant difference in the number of the
infected individuals in the asymptomatic stage,
infected individuals in pre-AIDS class, and infected
individuals in full-blown AIDS group while strategy
B it’s not positive impact observed in the infected
individuals in the asymptomatic stage and infected
individuals in pre-AIDS class.
ACKNOWLEDGMENT
The work was supported by DRPM RISTEKDIKTI,
Directorate General of Research and Development
Reinforcement, Ministry of Research, Technology,
and Higher Education in accordance with the Letter
of Appointment Agreement of Implementation of
Research Program No: 054/SP2H/LT/DRPM/2018.
REFERENCES
Joshi, H.R., 2002. Optimal control of an HIV immunology
model, Optimal Control Application Mathematics,
vol. 23, pp. 199-213.
Lenhart, S. and Workman, J.T., 2002. Optimal Control
Applied to Biological Models. London: Chapman
and Hall,
Marsudi, Hidayat, N., and Wibowo, R.B.E., 2017.
Application of optimal control strategies for the
spread of HIV in a Population, Research Journal
of Life Science, vol. 4 (1), pp. 1-9.
Marsudi, N. Hidayat, and Wibowo, R.B.E., 2017.
Sensitivity analysis of the parameters of an
HIV/AIDS model with condom education and
antiretroviral therapy, AIP Conference
Proceedings, vol. 1913 (1): 020019.
Marsudi, N. Hidayat, and Wibowo, R.B.E., 2018(a).
Optimal strategy for controlling the spread of HIV
dynamics with educational educations and
antiretroviral therapy, J. Phys.: Conf. Ser., vol.
1028 (012115).
Marsudi, N. Hidayat, and Wibowo, R.B.E., 2018(b).
Optimal strategy for controlling the spread of HIV
dynamics with educational educations and
antiretroviral therapy, J. Phys.: Conf. Ser., vol.
1028 (012115).
Okosun, K.O., Makinde, O.D., and Takaidza, I., 2013.
Impact of optimal control on the treatment of
HIV/AIDS and screening of unaware infectives,
Applied Mathematical Modelling, vol. 37, pp.
3802-3820.
Pontryagin, L.S., Boltyanskii, V.G., Gamkrelidze, R.V.,
and Mishchenko, E.F., 1962. The Mathematical
Theory of Optimal Processes, New York:
Interscience Publisher.
Sharma, S. and Samanta, G. P., 2015. Stability analysis and
optimal control of an epidemic model with
vaccination,” International Journal of
Biomathematics, Vol. 8, No. 3 (1550030).
Yusuf, T.T. and Benyah, F., 2011.Optimal strategy for
controlling the spread of HIV/AIDS disease: A
case study of South Africa,” Journal of Biological
Dynamics, vol. 6 (2), pp. 475-494.
Optimal Control of an HIV Model with Condom Education and Therapy
419