Pedagogical Values: Revealing Mathematics Teachers’ Belief and

Action in Teaching

Kamirsyah Wahyu

, Sri Subarinah

, Sofyan Mahfudy

, Dwi Ratnasari

1Faculty of Teacher Training and Education, Universitas Islam Negeri Mataram, Jln. Gajah Mada 100, Mataram,

Indonesia

2Faculty of Teacher Training and Education, Universitas Mataram, Mataram, Indonesia

3Faculty of Teacher Training and Education, Universitas Islam Negeri Mataram, Mataram, Indonesia

4Informatics Department, STMIK Bumigora Mataram, Mataram, Indonesia

Keywords: Pedagogical Values, Beliefs, Actions, Mathematics Teaching.

Abstract: The current research aimed to identify the pedagogical values (PVs) held by mathematics teachers and then

analyze on the factors that affect the PVs enacted in the classroom. It involved ten teachers in Madrasah who

have been teaching mathematics in the various period, from one year until over five years of experiences. Of

three teachers were purposively chosen that satisfy the values criteria to be further observed in classroom

teaching and interviewed. The teachers’ PVs were identified through communication, dialogue and pedagog-

ical reflections by means of the questionnaire, interview, focus group discussion, and classroom observation.

The data was then confronted with the values criteria (choosing, prizing, and acting) to determine the mathe-

matics teachers’ PVs. The research found that only two teachers satisfy the criteria, one teacher found diffi-

culties to enact his PVs and the others could not pass through prizing criteria. The research concluded that the

PVs held by the mathematics teachers are shaped by the specific need or condition of their students (culturally

dependent) and constraints such as values alignment and institutional values can affect the enactment of PVs.

The implication for educational program and school context will be discussed.

1 INTRODUCTION

Teaching and learning in the classroom involve three

primary elements, i.e., teachers, students and content

or well-known as didactic triangle (Steinbring, 2005).

Each element has its characteristics, e.g., the teachers

have in mind what would be done in the classroom to

make students understand the subject or content, the

students have the views on the subject and expect to

learn it in a specific ways so that she/he perceives the

subject as the essential part of their classroom experi-

ence, and the subject learnt and taught is value-laden.

Leu and Wu (2005) asserted that all of them are not

value-free. In fact, they are value-carriers

Value is another affective and sociocultural con-

struct which becomes a crucial yet neglected aspect

of mathematics education. There are not many re-

searches on values for the last decade in mathematics

education (Seah & Peng, 2012). Bishop (1991) shed

light on how the cultural aspects of teachers and stu-

dents contribute to mathematics learning. Research

projects such as VAMP (Values and Mathematics

Projects), VIMT (Values in Mathematics Teaching),

and Third Wave Project (Seah & Wong, 2012) were

further effort to understand the significance of values

in mathematics teaching and learning. The projects

revealed that what teachers and students valued in

mathematics and its teaching support the mathematics

learning. The researches (e.g., Kalogeropoulos &

Bishop, 2017; Seah & Andersson, 2015a) showed that

values alignment in mathematics classroom help stu-

dents’ engagement in learning. When students valued

achievement in mathematics learning, despite their

negative feeling toward the subject, it gives them a

sense of will and determination to work better in

mathematics (Seah, 2016; Zhang, Barkatsas, Law,

Leu, & Seah, 2016). The values students possessed in

mathematics learning might be an alternative reason

why students in Mainland China, Hong Kong, and

522

Wahyu, K., Subarinah, S., Mahfudy, S. and Ratnasari, D.

Pedagogical Values: Revealing Mathematics Teachers’ Belief and Action in Teaching.

DOI: 10.5220/0008524805220529

In Proceedings of the International Conference on Mathematics and Islam (ICMIs 2018), pages 522-529

ISBN: 978-989-758-407-7

Taiwan scored better in the international assessment

like PISA.

The classification of values by Bishop (2008);

mathematical values, mathematics educational val-

ues, and general educational ascertain mathematics

educators especially teachers that inculcating values

in mathematics teaching is highly possible. For exam-

ple, persistence is one of the mathematical educa-

tional values (Clarkson, Bishop, FitzSimons, & Seah,

2000). Mathematics teachers have the chance to de-

velop students' persistence, for example, in problem-

solving. Teaching values is in accordance with the

agenda of values or character education echoed in

many countries such as Indonesia.

Values and beliefs are closely related to affective

constructs (Lim & Kor, 2012). However, the differ-

ence is not always made clear (Bishop, Seah, & Chin,

2003). Hart (1989) defined beliefs as certain types of

judgments about a set of objects. “Teaching mathe-

matics is about explaining rules or formulas” is one

example of beliefs about mathematics pedagogy

(McLeod, 1992). Halstead and Taylor (2000) defined

values as “…principles and fundamentals convictions

which act as general guides to behavior, enduring be-

liefs about what is worthwhile… (p.3). Values repre-

sent a more internalized form of affect. It is the deep

affective qualities (Bishop et al., 2003). Kluckhohn

(1962) asserted that values differ from beliefs “…by

the commitment to action in situations involving al-

ternatives” (p.432). P. Clarkson and Bishop (1999)

stated that values are beliefs in action. Raths, Harmin,

and Simon (1987) concluded that a belief evolves into

value when it includes choosing, prizing, and acting.

If a teacher valued teaching mathematics is just about

explaining the rules or formulas, then it will be his/her

typical way of instruction in the classroom.

Researching values give alternative perspective in

improving mathematics learning since it deals with

beliefs in action held the teachers or what a worth-

while for the students in learning mathematics. Prior

researched on values have analyzed teachers’ planned

and espoused values (Lim & Ernest, 1997), teachers’

intended and implemented values (Bishop et al.,

2003), values as pedagogical identities (Chin, 2002;

Chin & Lin, 2000), tools used to access students’ and

teachers’ values in mathematics pedagogy (Dede,

2006, 2011), values related to effective mathematics

lessons (Seah & Wong, 2012), and alignment of val-

ues in mathematics classroom (Kalogeropoulos &

Bishop, 2017; Seah & Andersson, 2015a).

Chin (2002) and colleagues investigated values in

mathematics teaching. Chin and Lin (2000) focused

on identifying and interpreting pedagogical values of

mathematics teachers. Values were conceived as

“…teachers’ pedagogical identities which reveal prin-

ciples of each teacher’s choice and judgments con-

cerning the importance of using certain pedagogical

identities in her/his classroom teaching mathemat-

ics...” (p.91).

The prior researches (Chin, 2002; Chin, Leu, &

Lin, 2001; Chin & Lin, 2000; Leu & Wu, 2005, 2006)

on pedagogical values have not analyzed how stu-

dents valued mathematics and its learning (mathemat-

ics learning) and institutional values affect the teach-

ers to enact their values in teaching mathematics. The

current research attempted to fill the gap, analyzing

the two factors that affect mathematics teachers’ ped-

agogical values enacted in the classroom. We defined

pedagogical values in this research as the personal

conviction of teacher’s thought, choices, and action

concerning the importance of specific pedagogical

identities in teaching mathematics. It is about feeling,

beliefs, and action of teachers in teaching mathemat-

ics. Pedagogical identities here mean typical ways

teachers deliver his/her mathematics instruction. The

criteria of values, i.e., choosing, prizing, and acting

by Raths et al. (1987) will be used to examine the ped-

agogical values.

The research used values clarification for data

analysis to answer two questions, i.e., what PVs held

by mathematics teachers? And how students valued

on mathematics learning and institutional values af-

fect mathematics teachers when enacting their PVs in

the classroom? The current research strengthens the

prior research on values in general and contributes to

understanding the pedagogical values of mathematics

teachers and its practice in the classroom in specific.

Understanding teachers’ PVs is the crucial step to for-

mulate actions in improving mathematics teaching

and learning. In practices, mathematics teacher edu-

cation and the development program for in-service

mathematics teacher especially in Indonesia could

consider not only pedagogical/content knowledge but

also the clarification and refinement of pedagogical

values.

2 METHODS

This research used descriptive qualitative approach to

identify and analyze mathematics teachers’ PVs. The

subjects, ten mathematics teachers, were given a

questionnaire, interview, and focus group discussion.

The three methods are parts of dialogue, communica-

tion and pedagogical reflections as critical activities

in the process of value clarification (Chin et al.,

2001). We used value clarification (Chin & Lin,

2001) to identify and document teachers’ PVs. Val-

ues criteria (choosing, prizing, and acting) by Raths

Pedagogical Values: Revealing Mathematics Teachers’ Belief and Action in Teaching

523

et al. (1987) was utilized to examine the PVs. The

methods used in this research can be summarized in

Table 1.

The subjects teach mathematics in Islamic-based

schools called Madrasah (secondary school level).

Public schools are somewhat different from Mad-

rasah

mainly regarding number and kinds of subjects

but both apply the same national curriculum. In Mad-

rasah, there are additional subjects about Islam. Stu-

dents in Madrasah have more subjects than in public

schools. The nature of Madrasah related to mathe-

matics teaching will be elaborated in the discussion

section.

The indicators of each value criteria are as follow

(Chin et al., 2001):

a. Choosing; one’s free will to choose, choosing

from alternatives, and choosing by thoughtful

consideration

b. Prizing; being happy with the choice or affirm

the choice to others

c. Acting; repeated practices which form a pattern

of teaching

Table 1: Summary of research methods

Criteria

of PVs

Data collection

Choosing

Questionnaire and interview (Peda-

gogic reflection)

Prizing

Interview (Dialogue and communica-

tion)

Acting

Questionnaire, interview, and class-

room observation (Dialogue, communi-

cation, and pedagogic reflection)

The questionnaire aimed to document teachers’

choices in teaching mathematics. It is a semi-open

questionnaire consists of several questions. Two of

them are what are the important things to teach in

mathematics classrooms? And how do you typically

teach mathematics? The teachers are encouraged to

write their answer if they disagree with the options.

The two questions are very crucial to identify teach-

ers’ choices of given alternatives. The last item of the

questionnaire asked teachers to reflect on their teach-

ing experiences. They are required to explain how

they teach mathematics which represents his/her

identities or typical ways of teaching. This question

aims to reveal teachers’ action after choosing the al-

ternatives.

The interview attempted to confirm teachers’ an-

swers (choices) in the questionnaire and examine how

teachers prize their PVs. The result of interview and

There are two kinds of Madrasah in Indonesia, public and private

Madrasah. Both are managed under the Ministry of Religious Af-

fairs. Private Madrasah is managed by community-based

questionnaire are used to choose three teachers pur-

posively. The selected teachers showed consistent

PVs through their choosing (in questionnaire and in-

terview), prizing (in the interview), and acting (in the

questionnaire when writing a pedagogical reflection

on his/her typical ways of teaching mathematics and

interview). We interviewed the teachers in two focus

group discussion (FGD). We argued that FGD can be

communal pedagogic reflections where dialogue and

communication between researcher team and teachers

flexibly take place. It also aimed to examine the con-

sistency of teachers PVs. We then have in-dept inter-

view and classroom observation with the three teach-

ers to further understand their PVs and analyze fac-

tors that can be constraints in classroom practices.

3 RESULTS

What are the important things to teach in mathemat-

ics classroom?

The subjects had varied answers to the question,

but none of them give alternatives out of the given

options. In the interview, some teachers answered dif-

ferently to what they have chosen in the question-

naire. The summary of teachers’ choices and answers

are presented in Table 2 (Choosing column). The ten

teachers are coded as MT

to MT

How do you typically teach mathematics?

For the question, we did not provide any options

in the questionnaire. The teachers were required to

write his/her typical ways of teaching mathematics.

We believe that teachers’ responses are heavily based

on their experiences in teaching mathematics. Thus,

what they wrote is his/her identities in practice. Then

interview was administered to validate the responses.

Table 2 (Acting column) shows the result of question-

naire and interview.

Drawing from the results of questionnaire and in-

terview, the mathematics teachers’ PVs will be cate-

gorized based on consistency in choosing, prizing and

acting. Consistent means that teachers’ responses are

in accordance with the indicators of the three criteria

of pedagogical values or otherwise. Based on Table

2, it is found that two teachers satisfy the indicators.

One teacher is inconsistent in her response to inter-

view. One teacher is inconsistent with the 1

and 2

question. The other six teachers could not prize their

choices and action. They were not aware of having

the PVs by their explanation in the interview. In fact,

it was challenging to examine what teachers prize.

organization and mostly apply boarding system.

ICMIs 2018 - International Conference on Mathematics and Islam

524

We examined it through their reasonable explanation

for the choices and action in the interview.

Table 2 shows that only two teachers (MT

, MT

)

satisfy the criteria of pedagogical values. MT

has

over five years of experiences in teaching mathemat-

ics. She currently teaches in public Madrasah. MT

a junior teacher with a year experience. He teaches

mathematics in Madrasah with boarding system. He

also graduated from Islamic boarding school (Junior

and senior high school level).

One teacher (MT

) could prize his choice for what

importance in teaching mathematics. However, MT

had a different answer on what he typically did in the

classroom. MT

teaches mathematics in private Mad-

rasah. In the interview, MT

posed interesting expla-

nation why he could not enact what he valued in

mathematics teaching. MT

explained that some con-

straints related to students’ values and institutional

values. In addition to the reasons, we decided to in-

clude MT

as the third subject to be observed in class-

room teachings.

The classroom observation was done in one ses-

sion with each teacher following by interview. It

aimed to confirm the results of questionnaire and in-

terview. For MT

, we wanted to identify further what

he called as constraints in enacting PVs.

The classroom observation showed that MT

uti-

lized Islamic inheritance context (Faraid) to learn

fractions. He confirmed in the interview that "it is im-

portant to relate mathematics topic with Islamic con-

text since students valued mathematics as only set

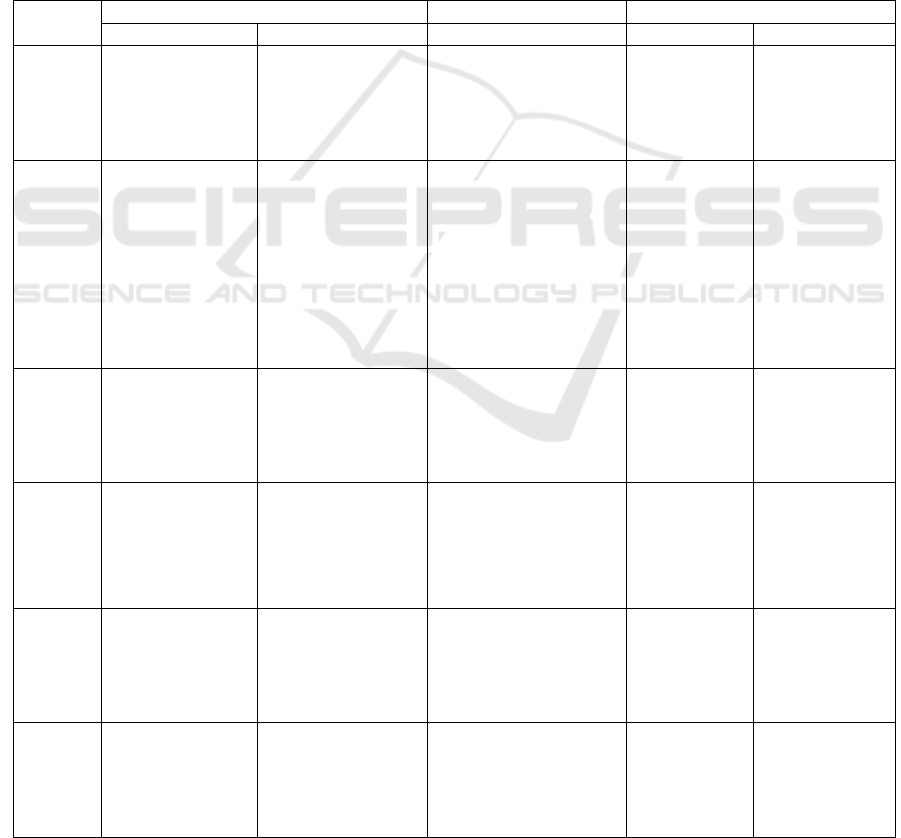
Table 2: Summary of subjects’ responses in questionnaire and interview

Subjects

Choosing

Prizing

Acting

Questionnaire

Interview

Questionnaire

Interview

A set of formulas

and its solution,

mathematics con-

cepts

Inculcation of val-

ues such as honesty

MT1 did not choose in-

culcation of values in the

questionnaire.

Using learning

tools made

from Delphi 7

Explain the

topic, give an

example and ex-

ercises

A set of formulas

and its solution,

mathematics con-

cepts, the applica-

tion of mathemat-

ics in daily life,

skill to solve

mathematics prob-

lems

Arithmetic skills, al-

gebra, and concepts

No prizing in the inter-

view

Explain the

topic related

to daily life,

give an exam-

ple and drill,

ask some stu-

dents to write

their answers

on the white-

board

Similar to ques-

tionnaire

Mathematics con-

cepts, the applica-

tion of mathemat-

ics in daily life

Mathematics con-

cepts

No prizing in the inter-

view

Explain the

topic, give

worked exam-

ple and exer-

cises

Similar to ques-

tionnaire

Mathematics con-

cepts, the applica-

tion of mathemat-

ics in daily life, in-

culcation of values

Mathematics con-

cepts, the applica-

tion of mathematics

in daily life, inculca-

tion of values

Able to confirm her

choice to others

Explain the

concept, relate

the topic to

daily life, in-

culcating the

values

Similar to ques-

tionnaire

Mathematics con-

cepts, the applica-

tion of mathemat-

ics in daily life

Mathematics con-

cepts, the applica-

tion of mathematics

in daily life

Able to confirm his

choice to others

Explain the

concept, relate

the topic to

daily life (Is-

lamic context)

Similar to ques-

tionnaire

The application of

mathematics in

daily life

The application of

mathematics in daily

life

Able to confirm his

choice to others

Explain the

topic, give

worked exam-

ple and exer-

cises

Similar to ques-

tionnaire

Pedagogical Values: Revealing Mathematics Teachers’ Belief and Action in Teaching

525

Subjects

Choosing

Prizing

Acting

Questionnaire

Interview

Questionnaire

Interview

A set of formulas

and its solution

A set of formulas

and its solution

Unable to confirm her

choice in the

Explain the

topic, give

worked exam-

ple and exer-

cises

Similar to ques-

tionnaire

of rules and nothing deals with daily life, and one of

the main reasons their parent sent their children here

is to learn religious teachings." He added that "I want

to show them that mathematics is not what they know.

And through the context, we can discuss the concept

of fraction and its operations.”

does understand the capability of her stu-

dents in mathematics. He said that “Only two or three

students could understand what I explain without re-

lating to their familiar context. My students do often

ask me about the use of mathematics for them. So, I

try to connect mathematics topics with something

they are familiar with.” MT

asked students to bring

snacks or plastics used for snacks to learn about netto,

bruto (net weight), and tara (the difference of netto

and bruto). MT

frequently emphasize to her students

that no matter what you do and get in mathematics,

the important one is you must be honest when you do

your task.

Unlike MT

and MT

, MT

had a somewhat diffi-

cult condition of teaching. In the observation, MT

started the lesson by explaining integers with the

number line, scaffold students to make number line,

ask students to place integers onto number line, give

examples of operating integers and give exercise.

told us that “I have tried bringing daily life or

context in my mathematics lesson. However, my stu-

dents could not get involved in that. They showed

lack of motivation in learning. Exercises or home-

work given were not accomplished. What an im-

portant thing for them is not to learn mathematics but

reciting and memorizing the Qur’an.”

In the schools, there is informal ‘consensus’

amongst students (not all) that nothing important than

learning the religion. Religion could save you in this

world and the later. The ‘consensus' is also directly or

indirectly influenced by the other teachers (non-math-

ematics). This condition also has been experienced by

while he was in Madrasah. MT

told that “a

great student was not a student who master the gen-

eral subject like mathematics or science but a student

who was able to memorize the Qur’an. So, mostly stu-

dents followed that way of thinking.”

4 DISCUSSIONS

In this part, we will analyze the level of value clarifi-

cation of MT

and MT

(Chin et al., 2001), constraints

that MT

had relating to what students valued on

mathematics learning or the notion of values align-

ment (Kalogeropoulos & Bishop, 2017; Seah & An-

dersson, 2015a, 2015b) and institutional values

(Bishop, 2008). In the last, we are going to discuss the

implication of the findings related to educational pro-

gram and schools’ context.

For MT

, connecting mathematics with students’

familiar context to show the application of mathemat-

ics in daily life and inculcation of values are im-

portant things to teach in the mathematics classroom.

In the interview, MT

explained the ability and need

of her students in learning mathematics. In this case,

she expressed her pleasure in those ways of teaching

mathematics and convinced the researchers and the

other teachers about her choices and actions in the

classroom. For MT

, introducing mathematics con-

cepts through Islamic context is the important thing

in teaching mathematics. He argued in the interview

that “using Islamic context to learn mathematics con-

cepts is the way to convince my students that mathe-

matics is not just a set of rules and formulas.”

What MT

and MT

chose in the questionnaire,

prized in the interview, and acted in classroom obser-

vation shows that they are aware of having the PVs.

Within that awareness of the importance of such val-

ues, they communicate them in the classroom with the

students and others in the interview. For example,

used the context of Faraid to teach fractions and

showed the use of mathematics through the

snack plastics. Both are not just the pedagogical value

carrier but value communicator.

The teacher who is aware of her/his values and

able to communicate it has a high level of value clar-

ification. The level of value clarification determines

the improvement that teacher can make in teaching

mathematics (Chin et al., 2001). However, the current

research did not further identify the changes that MT

and MT

make referring to their level of value clarifi-

cation.

The PVs held by MT

is affected by her students’

ability and need. When her students learned

ICMIs 2018 - International Conference on Mathematics and Islam

526

mathematics better by connecting to their familiar

contexts, MT

found that way of teaching is im-

portant. So, did MT

, when his students valued math-

ematics as just a set of rules and formulas, he used the

context of Faraid to teach fractions. This finding im-

plies that mathematics learning is a social-cultural ac-

tivity that involves close interaction between the

teachers and the students (Lim & Kor, 2012). A

teacher may hold various importance pedagogical

identities in teaching mathematics but only what

he/she enact in the classroom consistently which ac-

commodate what they valued become his/her PVs.

Although implementing similar national curricu-

lum, public schools are slightly different from Mad-

rasah in Indonesia. The difference is not only about

the number and kind of subject but also the emphasis

that the schools put on what the students should

achieve. For example, in some Madrasah with board-

ing system, mathematics is less important than recit-

ing and memorizing the Qur’an. A model student is a

student who knows lots of religious teachings. So,

each student wants to be in that position. This condi-

tion is what MT

experienced when he was in Mad-

rasah and MT

was facing in his school. Unfortu-

nately, we did not find any researches which empiri-

cally explain that condition in Indonesia. Bishop

(2008) called this as institutional values. He asserted

that the values that institutions have contributed to the

development of mathematical thinking in the differ-

ent group of students.

argued that such ‘doctrine' in the level of in-

stitution affect the way students perceived other sub-

jects like mathematics. He found his students have

less willingness to learn mathematics since it is less

important. However, we need further research to ex-

plore how institutional values affect students’ value.

What students valued on mathematics classroom dif-

fer from what the teacher valued is one of the causes

of students (dis)engagement in learning mathematics

(Kalogeropoulos & Bishop, 2017; Seah & Andersson,

2015a, 2015b). In this research, we did not document

students’ values to validate what MT8 underwent in

his practices.

In some scenes of the FGD, we discussed the pos-

sibility of inculcating values in teaching mathematics.

All teachers agreed that through mathematics teach-

ing, values could be taught. The teachers also showed

similar response about teaching values in the ques-

tionnaire. However, they did not have any idea how

to teach values and the values they know are limited

to general education values. For example, MT

incul-

cated honesty through direct speech in the class, not

as a part of mathematics activities.

The findings along with the status quo of institu-

tional values held by some Madrasah which affect the

PVs of MT

should be a concern by the mathematics

educators and the policymakers to support the im-

provement of mathematics teaching and learning. The

further efforts especially researches on the pedagogi-

cal values should be taken as they could support the

program of character education. We argued that,

based on the findings of the current research, mathe-

matics teacher education and the development of in-

service mathematics teacher programs should take

values issues into account (Chin, 2006). The research

on pedagogical values could be extended to other sub-

jects in specific and educational context in general,

e.g. school context (Husu & Tirri, 2007).

5 CONCLUSIONS

The research found that only two of the ten teachers

fulfill the values criteria. What teachers think and feel

as the worth in teaching mathematics falls onto the

beliefs. The two teachers have quite similar PVs re-

garding the use of context in teaching mathematics to

show their students that mathematics relates to their

daily life. However, they have a different situation

which develops their PVs. The first is students’ lim-

ited ability in mathematics, and there is a need to fa-

cilitate the ability by bringing daily contexts in math-

ematics teaching. The second is that the students val-

ued mathematics is just a set of rules and does not deal

with daily life. In this case, the mathematics teachers’

PVs are built on the adjustment of students’ condition

such as the ability in mathematics and the values they

have. Whether or not the teachers enact his/, her PVs

is affected by constraints such as what the students

valued on mathematics learning and institutional val-

ues. The existence of constraints closely relates to the

context of the institution (Madrasah). Further re-

search is needed to thoroughly examine how students’

values on mathematics and its learning, institutional

values and the enactment of teachers’ values relate

one another.

ACKNOWLEDGEMENTS

We would like to acknowledge LP2M Universitas Is-

lam Negeri (UIN) Mataram for funding the program

and mathematics teachers who are willing to partici-

pate in the interview actively, classroom observation

and accomplish the questionnaire.

Pedagogical Values: Revealing Mathematics Teachers’ Belief and Action in Teaching

527

REFERENCES

Bishop, A. (1991). Mathematical enculturation: A

cultural perspective on mathematics educa-

tion (Vol. 6): Springer Science & Business

Media.

Bishop, A. (2008). Teachers’ mathematical values for

developing mathematical thinking in class-

rooms: Theory, research and policy. The

Mathematics Educator, 11(1/2), 79-88.

Bishop, A., Seah, W. T., & Chin, C. (2003). Values in

mathematics teaching—The hidden per-

suaders? In Second international handbook

of mathematics education (pp. 717-765):

Springer.

Chin, C. (2002). Researching mathematics teachers’

pedagogical values: A synthesis of the three

Taiwanese studies. Paper presented at the

2nd East Asia Regional Conference on

Mathematics Education and 9th Southeast

Asian Conference on Mathematics Educa-

tion.

Chin, C. (2006). Conceptualising pedagogical values

and identities in teacher development: A

comparison of taiwanese and australian

mathematics teachers. In F. K. S. Leung, K.

D. Graf, & F. J. Lopez-Real (Eds.), Mathe-

matics Education in Different Cultural Tra-

ditions-A Comparative Study of East Asia

and the West (Vol. 9, pp. 537-547). Boston,

MA: Springer.

Chin, C., Leu, Y.-C., & Lin, F.-L. (2001). Pedagogical

values, mathematics teaching, and teacher

education: Case studies of two experienced

teachers. In F.-L. Lin & T. J. Cooney (Eds.),

Making sense of mathematics teacher edu-

cation (pp. 247-269): Springer.

Chin, C., & Lin, F.-L. (2000). A case study of a math-

ematics teacher’s pedagogical values: Use of

a methodological framework of interpreta-

tion and reflection. Proceedings of the Na-

tional Science Council, 10(2), 90-101.

Chin, C., & Lin, F.-L. (2001). Mathematics teacher's

pedagogical value clarification and its rela-

tionship to classroom teaching. Paper pre-

sented at the Proceedings of the National

Science Council Republic of China, Part D:

Mathematics Science and Technology Edu-

cation.

Clarkson, P., & Bishop, A. (1999). Values and mathe-

matics education. Paper presented at the 51st

Conference of the International Commission

for the Study and Improvement of Mathe-

matics Education, University College, UK.

Clarkson, P., Bishop, A., FitzSimons, G., & Seah, W.

T. (2000). Challenges and constraints in re-

searching values. Paper presented at the Pro-

ceedings of the twenty-third annual confer-

ence of the Mathematics Education Re-

search Group of Australasia Incorporated

held at Fremantle, Western Australia.

Dede, Y. (2006). Mathematics Educational Values of

College Students' towards Function Con-

cept. Eurasia Journal of Mathematics, Sci-

ence & Technology Education, 2(1), 82-102.

Dede, Y. (2011). Mathematics education values ques-

tionnaire for Turkish preservice mathemat-

ics teachers: Design, validation, and results.

International Journal of Science and Math-

ematics Education, 9(3), 603-626.

Halstead, J. M., & Taylor, M. J. (2000). The develop-

ment of values, attitudes and personal qual-

ities: A review of recent research: National

Foundation for Educational Research

Slough.

Hart, L. E. (1989). Describing the affective domain:

Saying what we mean. In D. B. McLeod &

V. Adams (Eds.), Affect and mathematical

problem solving (pp. 37-45). New York:

Springer.

Husu, J., & Tirri, K. (2007). Developing whole school

pedagogical values—A case of going

through the ethos of “good schooling”.

Teaching and Teacher Education, 23(4),

390-401.

Kalogeropoulos, P., & Bishop, A. J. (2017). What is

the role of value alignment in engaging

mathematics learners? Paper presented at

the 9th International confrence of Mathe-

matics Education and Society, Volos,

Greece: University of Thessaly.

Kluckhohn, C. (1962). Values and value-orientations

in the theory of action: An exploration in In

T. Parsons & E. A. Shils (Eds.), Toward a

general theory of action (pp. 388-433). New

York: Harper and Row.

Leu, Y.-C., & Wu, C.-J. (2005). Investigation on an

elementary teacher’s mathematics pedagog-

ical values through her approach to stu-

dents’errors. Paper presented at the 29th An-

nual Conference of the International Group

for the Psychology of Mathematics Educa-

tion, Melbourne, Australia.

Leu, Y.-C., & Wu, C.-J. (2006). The origins of pupils’

awareness of teachers’ mathematics peda-

gogical values: Confucianism and Bud-

dhism-driven. In F. K. S. Leung, K. D. Graf,

& F. J. Lopez-Real (Eds.), Mathematics

ICMIs 2018 - International Conference on Mathematics and Islam

528

Education in Different Cultural Traditions-

A Comparative Study of East Asia and the

West (Vol. 9, pp. 139-152). Boston, MA:

Springer.

Lim, C. S., & Ernest, P. (1997). Values in mathemat-

ics education: What is planned and what is

espoused? British Society for Research into

Learning Mathematics, 37.

Lim, C. S., & Kor, L. K. (2012). ‘Excellent’primary

mathematics teachers’ espoused and enacted

values of effective lessons. ZDM, 44(1), 59-

69.

McLeod, D. B. (1992). Research on affect in mathe-

matics education: A reconceptualization. In

D. A. Grouws (Ed.), Handbook of research

on mathematics teaching and learning (pp.

575-594). New York: Macmillan.

Philipp, R. A. (2007). Mathematics teachers’ beliefs

and affect. In J. F. K. Lester (Ed.), Second

handbook of research on mathematics teach-

ing and learning (Vol. 1, pp. 257-315). Char-

lotte, NC: Information Age.

Raths, L. E., Harmin, M., & Simon, S. B. (1987). Se-

lections from values and teaching. In P. F.

Carbone (Ed.), Value theory and education

(pp. 198-214). Malabar: Krieger.

Seah, W. T. (2016). Values in the mathematics class-

room: Supporting cognitive and affective

pedagogical ideas. Pedagogical Research,

1(2), 53.

Seah, W. T., & Andersson, A. (2015a). Teacher align-

ment of values in mathematics classrooms.

Paper presented at the Ninth Congress of the

European Society for Research in Mathe-

matics Education, Prague, Czech Republic.

Seah, W. T., & Andersson, A. (2015b). Valuing diver-

sity in mathematics pedagogy through the

volitional nature and alignment of values. In

A. Bishop, T. N. Barkatsas, & H. Tan (Eds.),

Diversity in mathematics education (pp.

167-183). Netherland: Springer.

Seah, W. T., & Peng, A. (2012). What students outside

Asia value in effective mathematics lessons:

A scoping study. ZDM, 44(1), 71-82.

Seah, W. T., & Wong, N. Y. (2012). What students

value in effective mathematics learning: a

‘Third Wave Project’research study. ZDM,

44(1), 33-43.

Steinbring, H. (2005). The construction of new math-

ematical knowledge in classroom interac-

tion: an epistemological perspective. New

York: Springer.

Wilkins, J. L. (2008). The relationship among ele-

mentary teachers’ content knowledge, atti-

tudes, beliefs, and practices. Journal of

Mathematics Teacher Education, 11(2), 139-

164.

Zhang, Q., Barkatsas, T., Law, H., Leu, Y., & Seah,

W. (2016). What primary students value in

mathematics learning: A comparative analy-

sis among the Chinese mainland, Hong

Kong, and Taiwan. International Journal of

Science and Mathematics Education, 14(5),

907-924.

Pedagogical Values: Revealing Mathematics Teachers’ Belief and Action in Teaching

529