The Effect of Angle of Attack and Chord Length of the Foil on Winged

Air Induction Pipe Optimization toward Drag Reduction by using

Numerical Approach

Yanuar

∗

, Muhammad Alief

, M. Akbar

, Fatimatuzzahra

, and Made

Department of Mechanical Engineering, University of Indonesia, Depok, Indonesia

Keywords:

Micro-bubble, Winged Air Induction Pipe (WAIP), foil, Angle of Attack, Chord Length, Drag Reduction.

Abstract:

In response to achieve better energy efﬁciency on the ship we propose the usage of air lubrication to reduce

ship drag. Winged Air Induction Pipe (WAIP) device that we used, will create micro-bubble to coat the bottom

of the ship by pulling air through induction pipe. Because of this phenomenon the drag reduction will occur.

The customization placement of the foil will give the different result of drag reduction experienced by plate

located after the foil. But, on this research we will see the different results of drag reduction caused by angle

of attack of the foil and its chord length. By using k-ω SST (shear stress transport) model on ANSYS 2-D

ﬂuent in our numerical simulation we can see how those customization and setup affect the result. On the

analysis we see the correlation between chord length and angle of attack of the foil that give most efﬁciency

for the ship. With this setup the drag reduction reach 3% of efﬁciency.

1 INTRODUCTION

Ships are the most important aspect on the distribution

of goods all around the world. According to Hydros

Foundation, there are 50.000 Cargo ships that sail ev-

ery day. All of those ships burn around 150 to 300

tons of fuel each day and produce 120 million tons of

carbon dioxide emission gas every year. Even though

it creates such an efﬁcient way on transferring goods,

it becomes such the biggest contributor on why global

warming happens.

Many efforts have been taken to reduce the con-

sumption of fuel and emission gases. One of which

is by reducing the resistances of ship so that the en-

ergy needed by ships will be much lesser. Huge im-

pact given by friction resistance makes it one of main

components needed to be reduced. Reducing friction

resistance can obtain bigger velocity, save more en-

ergy over the pump system, increase efﬁciency, re-

duce fuel consumption and minimize the operational

bill as well as the emission gases (Pang et al., 2014).

Speaking of which, there are 2 components that

affect ship’s friction resistance which also reduce the

velocity of the ships, they are water density and wet-

ted surface area of the hull. Reducing local water

density can be attained by layering up the ship’s hull

with micro-bubble so that can lower the mean density

of two phases ﬂow in the boundary layer when the

ﬂow is turbulent (Uhlman, 1987; Yanuar et al., 2012;

Zhang et al., 2018). Therefore, the reduction of lo-

cal water density makes not only its viscosity much

lower, but also make the Reynold shear stress.

This method of air lubrication is proved that it is

able to reduce the ship’s friction resistance up to 10-

15% (Kodama et al., 2000). However, this reduction

is accompanied by the undeniable energy needed to

inject micro-bubble into the water. This energy re-

quired adiabatic compression energy, the energy to

generate micro-bubble and mechanical losses in the

compressor (Kumagai et al., 2015). Hence, it causes

the net total reduction around 0-5% and hampers the

application of the full scale ship.

To overcome this, Kumagai et al. (2015) used bub-

ble generating device called Winged Air Induction

Pipe (WAIP). Hydrofoil was attached below micro-

bubble injector to create low pressure area on the up-

per surface of the hydrofoil when the ship was trav-

elling. The low pressure could make the atmospheric

air enter the ﬂow without using compressor. Yet, there

are some variables required, they are shapes and di-

mension of the hydrofoil, angle of attack, clearance

between WAIP to the hull, ﬂow types, etc. These re-

late to the relationship among variables which is difﬁ-

cult to imagine, so that the determination of how high

Yanuar, ., Alief, M., Akbar, M., , F. and , M.

The Effect of Angle of Attack and Chord Length of the Foil on Winged Air Induction Pipe Optimization toward Drag Reduction by using Numerical Approach.

DOI: 10.5220/0008543401190125

In Proceedings of the 3rd International Conference on Mar ine Technology (SENTA 2018), pages 119-125

ISBN: 978-989-758-436-7

119

or low the variables to make the most possible opti-

mum rate is still hard to be deﬁned. Besides, for those

bigger ships which have deep full water, pressure cre-

ated is not so low, so additional blower is needed to

maximize micro-bubble injection.

On their research, Kumagai et al. (2011) used

angle of attack variations by the magnitude about

◦

,16

◦

,and 20

◦

with the same length hydrofoil and

injection hole. However, length required for the hy-

drofoil was not elaborated brieﬂy. Therefore, this re-

search is going to make variation on the same amount

of angle of attack about 12

◦

,16

◦

,and 20

◦

but with

length variation of hydrofoil around 30,35,40,45,50

[mm], so that can generate different data variation

each angle of attack in every length of hydrofoil. Con-

sequently, it can be taken from optimal angle of attack

and length of hydrofoil to reduce the resistances of the

ship.

2 THEORY

2.1 Experimental Theory

The moving foil in a ﬂow will result in the negative

pressure of the area in the foil surface (Ockfen and

Matveev, 2009). Then, atmospheric air will be pulled

when the negative pressure value made higher than

the hydrostatic pressure (Series A, 1779), where

∆P ≥ ρgh (1)

where

∆P = 1/2C

ρU

(2)

and

ρgH = (ρ − ρ

air

)gH (3)

In sequencing, C

is the negative pressure coefﬁ-

cient in the foil, ρ is the density of ﬂuid, U is velocity

of the ﬂuid and H is the distance from draft to the

WAIP installed area.

However, the higher the value of ∆P does not de-

termine that the bubble will be formed. So that we

should still watch the limit of how ﬂuid stream by

U ≥ U

(4)

where

∼

2gH

(5)

Therefore, from the formula above, we can notice

that it is the value of C

which determines whether

in certain condition the bubble will be formed or not.

In addition, the higher the C

value, the higher the

value of P will be while the U

will be smaller. In

other words, the ﬁrst requirement of drag reduction

creation will be fulﬁlled (Cui et al., 2003)(Shereena

et al., 2013). This is due to the effect of how high the

value of U compare with the value of U

when the

bubble is created, which has been proved by Kumagai

et al. (2015).

From the WAIP experiment in towing tank Kuma-

gai et al. (2010) the injected energy will be smaller

when meeting this formula:

α >

∼

sinθ (6)

when L, h

and θ in sequence are cord length, air

bubble mixed layer, thickness, and angle of attack of

hydrofoil. With this formulation, L and θ in foil ad-

equately affect the amount of C

value. Net power

saving will be greater if the value of C

is also

greater (Kumagai et al., 2015). Therefore, by arrang-

ing L and θ foil, we will manage to get the same value

of C

as we expected then it will result in the highest

net power saving in this phenomenon.

Besides, to understand whether a WAIP is able to

create bubble or not, we can look at how the energies

working in the installed tool area. If the W

otal gets

zero, it can be concluded that there is bubble without

extra injection.

total

= W

−W

(7)

is the variable which describes the energy needed

to inject bubble into the stream when the energy de-

termined by how deep the installed tool are (H) and

the ﬂux volume (Q)

= ρgHQ (8)

is the variable representing the negative energy

obtained by the the installment of WAIP (foil). The

value of W

is determined by how great the C

value

and certain ﬂow velocity (U).

= 1/2C

ρU

Q (9)

represents the energy formed when the Drag force

in WAIP (foil) installed. C

in the foil and the area of

the foil contacted with ﬂuid determine the value of

= 1/2C

ρU

A (10)

Hence, the energy forming the bubble will touch the

zero point if the value of C

in the foil is as high as

possible and the value of C

is as low as possible.

SENTA 2018 - The 3rd International Conference on Marine Technology

120

2.2 Computational Theory

Along with set-up when has been prepared, there are

some formulations which can explain how this set-up

is able to represent the model being made. By using

RANS Reynold Averages Navier Stokes Equation we

can simulate how the ﬂow visualised in our simula-

tion. RANS is an equation that explain how the ﬂow

and its component happen. It also describes many

phenomenons such as transient, viscous, incompress-

ible, two phase ﬂow and three dimensional (Muste

et al., 2009). The formulation is described as follow :

∇U = 0 (11)

δρU

δt

+ ∇(ρUU

) = −∇p∗ + ∇(µ∇U)+ ∇(ρτ) + S

(12)

where U = (u

+ u

) is the velocity vector. t

is time. ∇ is vector differential factor. p

∗

is rela-

tive pressure. ρ and µ are ﬂuid properties the density

and the dynamic viscosity, respectively. τ is Reynold

stress tensor for turbulence ﬂow, which we will be

using the k-ω SST equation for this research. With

many factors and considerations we use the k-ω SST

to be our main method and equation on this research.

2.2.1 SST k-ω

Generally, Shear-Stress Transport (SST) k-ω is em-

ployed as the modelling. In the consideration that

this modelling can calculate more accurately on the

turbulent ﬂow near the wall, then this also correct

in the advanced way relating to the roughness effect

in the skin friction and thermal ﬂux which occur on

the modelling process (Olazabal-Loum

e et al., 2017).

Roughness is being essential since it is the rough-

ness which causes the friction resistance, the alter-

ation of ﬂow formation and the velocity difference in

the boundary layer. These points should be consid-

ered and emended, reckoning that the foil passing the

ﬂow will bear the phenomena above. Furthermore,

this model can simulate directly two turbulence to-

wards the wall boundary instead of correlating near

wall and far ﬁeld region by empirical wall function

(Mohanarangam et al., 2009). The formulation is de-

scribed as follow; Kinematic Eddy Viscosity

max(a

ωSF

(13)

Turbulence Kinetic Energy

δk

δt

δk

δx

= P

− βkω +

δx



(ν + σ

)

δk

δx



(14)

Speciﬁc Dissipation Rate

δω

δt

δω

δx

= aS

− βω

δx



(ν + σ

)

δk

δx



+ 2(1 − F

)σ

ω2

δk

δx

δω

δx

(15)

The turbulence kinetic energy k and speciﬁc dis-

sipation rate w are estimated from the boundary con-

dition of turbulence quantities turbulence intensity I

and length scale l, where the formulation is ;

k =

avg

(16)

and

ω =

1/2

1/4

(17)

Due to the differences in ﬂow phases after air

sucked in to the water and its mass velocity, the com-

parison of volume of ﬂuid and how the bubble enter-

ing the water, this mixed ﬂow needs to be watched on

how momentum happening in every phases. Besides,

to get the ﬂow following its compressibility, mixing

reactions, and mixture fraction as well as in the turbu-

lence ﬂow, we need to record it so that those can be

explained using the formulations below;

Continuity equation of diffusion

δt

(ρ

) + ∇(ρ

−→

) = 0 (18)

where

−→

is the mass velocity as follow;

−→

∑

k=1

−→

(19)

where ρ

is the diffusion of density described as fol-

low:

∑

k=1

(20)

where a

is volume fraction of the phase k.

Therefore the density distinction of the bubble for-

mation of foil will be answered. Consequently, the

density counted is not homogeneous in every situa-

tion. It also says that the density counted is not ho-

mogeneous in every situation.

Due to its curvature the upper surface foil will own

distinctive velocity. Then, its ﬂow will pull the atmo-

spheric air in. This ﬂow, both mixed and not, will

have heterogeneous density where the ﬂowed mass

will be different. Furthermore, velocity will also be

different, especially on upper and below surface foil.

Therefore momentum will be created in the ﬂow. The

following is the formulation used in the modelling of

SST k-ω this time.

The Effect of Angle of Attack and Chord Length of the Foil on Winged Air Induction Pipe Optimization toward Drag Reduction by using

Numerical Approach

121

δt



−→



+ ∇



−→



= −∇p + ∇





∇

−→

+ ∇

−→



+ ρmg +

−→

F + ∇

∑

k=1

−→

dr,k

−→

dr,k

(21)

where, n is number of phases,

−→

F is body force and

is the viscosity of the diffusion. Since the mixed

viscosity is not homogeneous, therefore;

∑

k=1

(22)

−→

dr,k

is drift velocity for secondary phase k, where;

−→

dr,k

−→

−

−→

(23)

where ν

deﬁned the dynamic viscosity of the k phase.

The relative velocity is deﬁned as the velocity of a

secondary phase p relative to the velocity of the pri-

mary phase q.

−→

−

−→

(24)

The mass fraction of any phase k given as :

(25)

Drift velocity and relative velocity

−→

q con-

nected by:

−→

dr,p

−→

−

∑

k=1

−→

(26)

From the previous continuity equation for sec-

ondary phase p, the volume fraction of the secondary

phase p can be obtained as :

δt

(α

) + ∇(α

) = −∇(α

dr,p

)

∑

k=1

( ˙m

− ˙m

)

(27)

where ˙m

and ˙m

is the mass ﬂow rates. Drift veloc-

ity is important to be inserted due to the ﬂow which

contacts with the plate will have different velocity.

3 COMPUTATIONAL DOMAIN

The model used is a plate with a dimension of 5000

mm in length with a thickness of 200 mm with a mod-

iﬁcation of the manufacture of 80 mm wide holes and

the addition of hydrofoil at a coordinates of 2.216 mm

from the bow section (Kumagai et al., 2010). The

Figure 1: Model and WAIP Attachment View from z+

Figure 2: WAIP Design

Modeling is using the Autodesk Inventor 2018 soft-

ware. Details of the model created can be seen in the

picture.

The WAIP device that we used is the NACA

653 - 618 proﬁle according to the power reduction

experiment using hydrofoil (Kumagai et al., 2015).

Boundary condition in this simulation has a dimen-

sion where the inlet part is placed 1-2 Lpp in front of

the hull direction, the outlet part is 3-5 Lpp from the

stern, and the exterior is 1 Lpp from the keel and up-

per exterior is 0.5 Lpp from keel (ITTC, 2011). More

grid numbers does not always produced better numer-

ical results (Gebreslassie et al., 2012). Therefore, a

Grid Independency Analysis (GIA) method is used

to ﬁnd out the right meshing method. Determination

of the right mesh size using the Grid Independency

Analysis (GIA) method by comparing the results with

the experimental results (Kumagai et al., 2015) with a

similar model as a form of initial validation.

Figure 3: Boundary Condition

SENTA 2018 - The 3rd International Conference on Marine Technology

122

Figure 4: Meshing Model

Figure 5: Zoom In of Meshing Model

4 SETUP (GRID AND

DISCRETIZATION) AND

VALIDATION

4.1 Setup (Grid and Discretization)

At the ﬁrst time, we have to choose which resolution

of grid we want to use. Because, good results depends

on good quality of meshing. To determine the quality

of the grid, we can use y+ equation ;

∆y

(28)

where ∆y is the distance from the ﬁrst node to the

wall. It is important to now about y

, where it

is determine the accuracy of the numerical simula-

tion alongside with grid density (Gebreslassie et al.,

2012). Smaller y

means more sensitive the grid it-

self. On the other hand, to achieve the efﬁciency of

simulating we have to ﬁnd which grid sensitivity and

which quantity of meshing the result had already con-

verged. As we can see on the Table 1. Because the

results had already converged on ﬁne till ﬁnest with

slightly different result, we use the grid quantity that

give the result before the converging happen.

4.2 Validation

To see how valid the results are, we compare it with

other journal experimental results. By using the same

properties of the ship and the foil, we compare our

numerical results with the experimental results done

by Kumagai et al. (2015). To achieve below 10% of

error, we used trial and error methods to see which

setup has the closest results as possible. By making

the same condition as the experimental results done

by Kumagai et al. (2015) we got that our setup re-

sults having errors below 10%, as described in table

1. From the Table 1. we can see that our average error

is 1,93% which is acceptable to continue our numeri-

cal setup (Duncan, 1981).

5 RESULTS AND DISCUSSIONS

The result that we got is the force acting on plate c

which is the viscous drag that acting along the plate.

The focus is on the drag reduction caused by the

WAIP that vary on the chord length and angle of at-

tack by compare it with the viscous drag acting along

the plate without WAIP installed. The relation be-

tween chord length, angle of attack and drag reduc-

tion can be depicted on Table 1 which θ, U, D

, ∆D

and D

is angle of attack of the foil, water inlet speed,

total drag on plate c, drag reduction and drag reduc-

tion percentage on plate c respectively.

On the angle of attack, the less drag reduction that

we got caused by the depression (w) which is bigger

as the tip of the foil tend to go deeper as the increase

of the angle. Besides the creation of the bubble by the

ﬂow is getting harder, the mixing ﬂow between air

and ﬂuids mostly appeared on the after position of the

foil. Moreover, bigger angle of attack make the up-

coming ﬂow from x+ axis hit the foil wall much big-

ger. Which make the ﬂow harder to cross and hardly

pulling air into the ﬂow.

By using ANSYS post-processing, the creation of

bubble can be seen by looking on the pressure area.

On the image, the low pressure area mostly occur on

the upper surface of the foil and after the foil which

is located below the plat c and coated it. By using the

volume of ﬂuid model on this setup, the differences

between pressure occur among regions caused by the

2 phases ﬂow between air and ﬂuid. Between those

ﬁgure we can see that the attachment of 20

◦

50mm

foil produce more low pressure than the attachment

of 12

◦

40mm.

Table 1: Error Percentage of Setup Results

Type θ Db (Exp) Db (Num) ∆Db %Error

Bare Bare 181.485 173.55 -7.935 -4.37

WAIP 12 167.751 168.241 0.49 0.29

WAIP 16 166.77 168.331 1.56 0.94

WAIP 20 164.808 168.281 3.47 2.11

Error 1.93

The Effect of Angle of Attack and Chord Length of the Foil on Winged Air Induction Pipe Optimization toward Drag Reduction by using

Numerical Approach

123

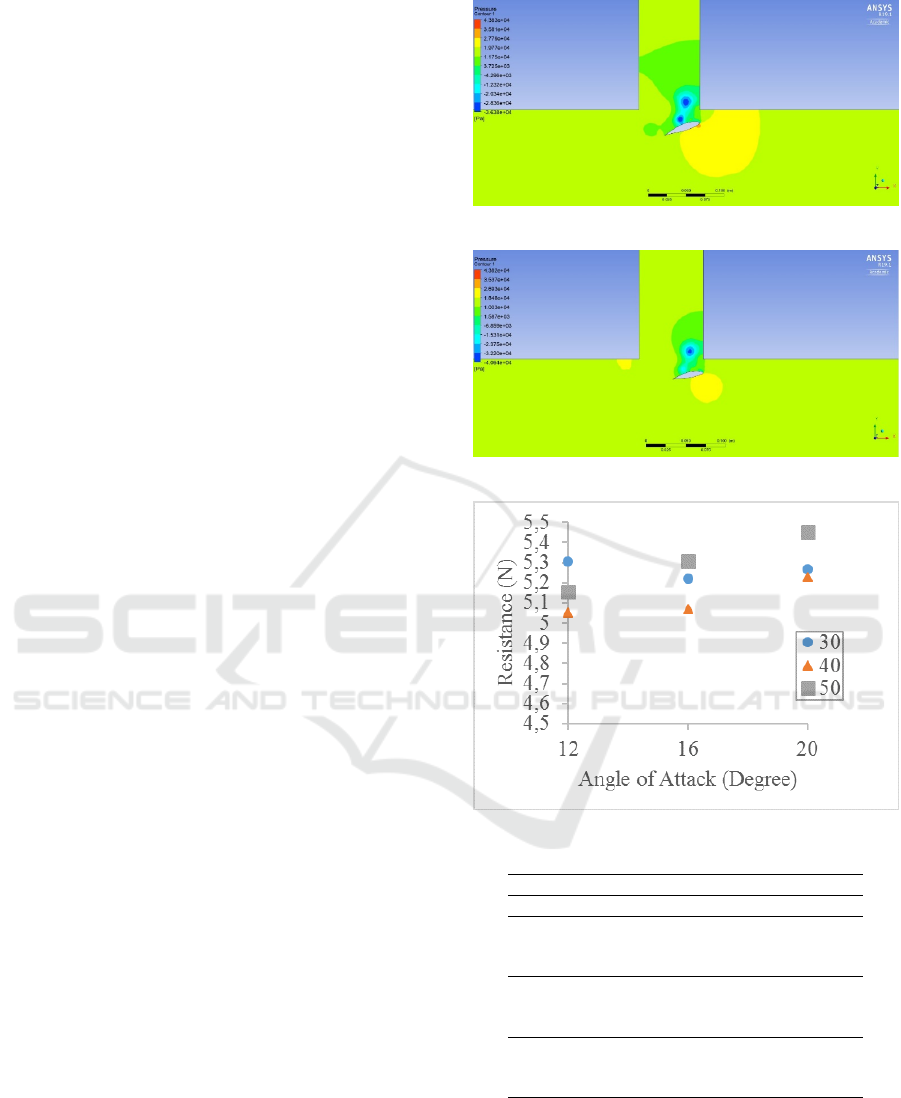
On 30 mm foil’s chord length the increase of the

angle of attack decrease the force experienced by the

plat. The biggest drag reduction output comes from

the biggest angle of attack used, by 3.13% DR. On

40 mm chord length it gives the same trend result,

so the biggest drag reduction output alos comes from

the biggest angle, with 3.103% DR. This trend also

happen on 50 mm foil’s chord length, with 3.24% DR.

This phenomena explain the bigger C

value

the bigger net power saving value done by Kumagai

et al. (2015). Where on 6

formula, we can see that

the C

value relatively bigger as the increase of

the chord length and the angle of attack. However,

we cannot conclude that bigger angle of attack and

longer chord length of the foil surely produce big-

ger drag reduction on plate E. We can see the lowest

drag reduction that is obtained is on the middle of the

chord length range. We can also see the fact that on

chord length 30mm, the correlation of bigger angle

can obtain bigger drag reduction is cannot be said as

a globally correct argument. But the same phenom-

ena does not apply to the changing chord length with

the same value of angle of attack. On the same degree

(angle of attack) variable except 12

◦

the biggest Drag

Reduction output still coming from the biggest chord

length. But the trend is different, where the second

biggest drag reduction output does not come from 40

mm foil’s chord length yet it comes from the smallest

foil’s chord length of 30 mm. On the other hand, the

resulted data on 12

◦

variable shows us that the biggest

drag reduction occurs on 30 mm, the second biggest

drag reduction comes from 50 mm, still the smallest

drag reduction is coming from 40 mm chord length.

The chord length of the foil that varied is affecting

the Reynold number on the foil which is affect the

coefﬁcient pressure. Bigger coefﬁcient pressure that

the foil can obtain produce bigger negative pressure

on the back of the foil that affecting the entertaining

of atmospheric air as can be seen on Figure 1. The

effect of Reynold number on coefﬁcient pressure of

the foil cannot be 100% predicted especially on big

angle of attack. Therefore, the appropriate design can

be obtained by using trial and error method.

The changing of drag reduction that occurs on the

plate comes from the ﬂow produced by the foil. The

characteristic of ﬂow which was occurring on plate

will occur differently because of the properties of the

foil itself. This properties of the foil occur because

of the changing of the chord length. Then the chang-

ing of the chord length make the Reynold Number of

the ﬂow occurred differently. Which is also makes the

different-kind of boundary layer. This unique charac-

teristic of the foil has already been explained in the

foil’s curve data (Naca Properties).

Figure 6: Pressure Area Condition 1

Figure 7: Pressure Area Condition 2

Figure 8: Drag Reduction

Table 2: Numerical Result of Inﬂuence of Hydrofoil

θ U (m/s) Db (N) ∆ Db DR (%)

bare 5.6 173.55 - -

12 5.6 168.2417 -5.3083 3.059

16 5.6 168.3313 -5.2187 3.102

20 5.6 168.2817 -5.2683 3.130

12 5.6 168.4979 -5.0521 3.002

16 5.6 168.479 -5.071 3.010

20 5.6 168.3218 -5.2282 3.103

12 5.6 168.3492 -5.1558 3.063

16 5.6 168.2437 -5.3063 3.151

20 5.6 168.0972 -5.4528 3.241

6 CONCLUSION

From this research we can see that bigger angle will

give lesser drag reduction on the plat c while the

longer the chord length give bigger drag reduction on

SENTA 2018 - The 3rd International Conference on Marine Technology

124

the plat c. On the other hand, smaller drag reduction

just make the air entrances the ﬂow a bit harder and

longer chord length of the foil just make the resis-

tance appendages slightly bigger. In this research we

choose the angle of attack 20

◦

and chord length 50 mm

because they were giving the biggest amount of drag

reduction among others by 3.241% drag reduction. In

the future, we hope that the friction losses which is

occur on the foil will be in the future journal.

ACKNOWLEDGEMENTS

Authors are thanks to Department of Mechanical En-

gineering, Faculty of Engineering, Universitas In-

donesia for making facility available and also grant

PITTA No. 2561/UN2.R3.1/HKP05.00/2018.

REFERENCES

Cui, Z., Fan, J. M., and Park, A.-H. (2003). Drag coefﬁ-

cients for a settling sphere with microbubble drag reduc-

tion effects. Powder technology., 138(2):132.

Duncan, J. H. (1981). An Experimental Investigation of

Breaking Waves Produced by a Towed Hydrofoil. Pro-

ceedings of the Royal Society of London. Series A, Math-

ematical and Physical Sciences, 377(1770):331–348.

Gebreslassie, M., Tabor, G., and Belmont, M. (2012). Cfd

simulations for sensitivity analysis of different parame-

ters to the wake characteristics of tidal turbine. Open J.

Fluid Dyn., 2.

Kodama, Y., Kakugawa, A., Takahashi, T., and Kawashima,

H. (2000). Experimental study on microbubbles and their

applicability to ships for skin friction reduction. Inter-

national Journal of Heat and Fluid Flow International

Journal of Heat and Fluid Flow, 21(5):582–588.

Kumagai, I., Kushida, T., Oyabu, K., Tasaka, Y., and Murai,

Y. (2011). FLOW BEHAVIOR AROUND A HYDRO-

FOIL CLOSE TO A FREE SURFACE. Vis Mech Proc

Visualization of Mechanical Processes, 1(4).

Kumagai, I., Nakamura, N., Murai, Y., Tasaka, Y., and

Takeda, Y. (2010). A new power-saving device for air

bubble generation: hydrofoil air pump for ship drag re-

duction. In Proceedings of the International Conference

on Ship Drag.

Kumagai, I., Takahashi, Y., and Murai, Y. (2015). Power-

saving device for air bubble generation using a hydrofoil

to reduce ship drag: Theory, experiments, and applica-

tion to ships. Ocean Engineering, 95:183 – 194.

Mohanarangam, K., Cheung, S. C. P., Tu, J. Y., and Chen,

L. (2009). Numerical simulation of micro-bubble drag

reduction using population balance model. Ocean Engi-

neering, 36(11):863 – 872.

Muste, M., Yu, K., Fujita, I., and Ettema, R. (2009). Two-

phase ﬂow insights into open-channel ﬂows with sus-

pended particles of different densities. Environmental

Fluid Mechanics, 9:161–186.

Ockfen, A. E. and Matveev, K. I. (2009). Aerodynamic

characteristics of NACA 4412 airfoil section with ﬂap in

extreme ground effect. International Journal of Naval

Architecture and Ocean Engineering, 1(1):1 – 12.

Olazabal-Loum

e, M., Danvin, F., Julien, M., and Aupoix,

B. (2017). Study on k-w shear stress transport model

corrections applied to rough wall turbulent hypersonic

boundary layers.

Pang, M. J., Wei, J. J., and Yu, B. (2014). Numerical study

on modulation of microbubbles on turbulence frictional

drag in a horizontal channel. Ocean Engineering, 81:58

– 68.

Series A (1779). Mathematical and Physical Science. Num-

ber 377.

Shereena, S. G., Vengadesan, S. N., Idichandy, V. G., and

Bhattacharyya, S. K. (2013). Cfd study of drag reduction

in axisymmetric underwater vehicles using air jets.

Uhlman, J. S. (1987). The Surface Singularity Method Ap-

plied to Partially Cavitating Hydrofoils. Journal of Ship

Research, 31(02):107–124.

Yanuar, Gunawan, Sunaryo, and Jamaluddin, A. (2012).

Micro-bubble drag reduction on a high speed vessel

model. Journal of Marine Science and Application,

11(3):301–304.

Zhang, J., Yang, S., and Liu, J. (2018). Numerical investi-

gation of a novel device for bubble generation to reduce

ship drag. International Journal of Naval Architecture

and Ocean Engineering, 10(5):629 – 643.

The Effect of Angle of Attack and Chord Length of the Foil on Winged Air Induction Pipe Optimization toward Drag Reduction by using

Numerical Approach

125