Strength Analysis of Glass Fibre Reinforced Plastics B-series

Propeller for Traditional Purse Seine Boat in the North Coastal

Region of Central Java Indonesia

Aulia Windyandari

, Gunawan Dwi Haryadi

, Ahmad Fauzan Zakki

and Insanu Abdilla Cendekia Abar

Industrial Technology Department, School of Vocation, Diponegoro University, Indonesia

Mechanical Engineering Department, Faculty of Engineering, Diponegoro University, Indonesia

Naval Architecture Department, Faculty of Engineering, Diponegoro University, Indonesia

Keywords: Finite Element Method, Standard B-series Propeller, Computational Fluid Dynamic, Plastic Glass Reinforced

Materials.

Abstract: In the previous study, the standard B-series propeller was developed to improve the propulsion performance

of the traditional purse seine boat in the North Coastal Region of Central Java. Since the developed propeller

design was adopted glass reinforced plastics material, therefore it is important to evaluate the strength

performance due to its application as a propulsion system. The aim of the research is to investigate the

structure response of the developed standard propeller that would be applied to the fishing boats typically

found in the North Coastal Region of Central. Finite element method (FEM) and computational fluid dynamic

analysis (CFD) for assessing the stress distribution and the maximum deformation of the standard was

performed. The loading condition of the propeller model is determined by using the pressure which is exerted

on the propeller that is provided by CFD analysis. The stress distribution and the maximum deformation

responses will be discussed.

1 INTRODUCTION

Recently, the standard B-series propellers designs

have been developed to improve the propulsion

performance of traditional purse seine boat in the

North Coast Region of Central Java (Windyandari,

2018). As a part of the research work, this paper is

focused on the investigation of structure responses of

the developed B-series propeller that using glass fiber

reinforced plastic as the material. In order to obtain a

reliable result, the process of assessing the structure

response of the propellers involves a complex

numerical analysis. Numerical analysis and

simulation is an iterative procedure that able to solve

complex problems with reliable and accepted

accuracy for predicting and estimating the exact

behaviour. As the propeller geometry is complex and

its loading conditions are more complicated, therefore

the structural response analysis should performed

with the complex computational method. Hence for

the pressure load, the computational fluid dynamics

analysis is conducted to obtain the pressure

distribution on the propellers. The complex

geometries structure analysis can be carried out by

adopting the finite element method, where the

propeller blade can be modelled as a beam, shell and

solid elements.

2 LITERATURE REVIEW

The propeller design involved complex geometry.

Some of studies are obtained to solve the complex

geometry in the structure analysis. Taylor et. al

introduced a technique that was known as elementary

beam theory which is treated the propeller blade as a

cantilever to the propeller hub (Taylor, 1993). Cohen

was proposed a simplified propeller blade model

using a helicoidally shell with infinite width (Cohen,

1955). However the approach method is not suitable

for a shell with finite width. In other studies, it is also

observed that the analytical methods based on

conventional mechanics do not offer a significant

improvement result for estimating and predicting the

Windyandari, A., Haryadi, G., Zakki, A. and Abar, I.

Strength Analysis of Glass Fibre Reinforced Plastics B-series Propeller for Traditional Purse Seine Boat in the North Coastal Region of Central Java Indonesia.

DOI: 10.5220/0008565401490152

In Proceedings of the 6th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management (ISOCEEN 2018), pages 149-152

ISBN: 978-989-758-455-8

149

stress of the propeller blade, instead of it is involved

for merely routine design activities (Connolly, 1961;

Atkinson, 1968; Wereldsma, 1965; McCarthy, 1969;

Boswell, 1969).

Since the analytical method have some limitation,

therefore numerical and computational technique

such as finite element method (FEM) and

computational fluid dynamic (CFD) analysis is

adopted to conduct the propeller performance

analysis. Some of research work is reviewed to shows

the role of finite element method in marine structure.

Sontvedt (1974) have studied the prediction of quasi

static and dynamic stress of marine propeller blade.

Young adopted a coupled boundary element method

(BEM) and finite element method to study the hydro-

elastic behaviour of the flexible composite propeller

in wake flow (Young, 2007). In the other study,

Young presented the structure response of flexible

composite propellers using fluid-structure interaction

analysis (Young, 2008). Blasques (2010) tailored the

laminate for controlling the blade deformation and the

developed thrust. Hong (2017) studied the

performance and efficiency of the 438x series of

composite propellers using finite element method and

computational fluid dynamics method (CFD). The

application FEM also can be found in the vibration

and buckling analysis of the marine structure (Yudo,

et.al. 2017; Windyandari, et.al. 2018).

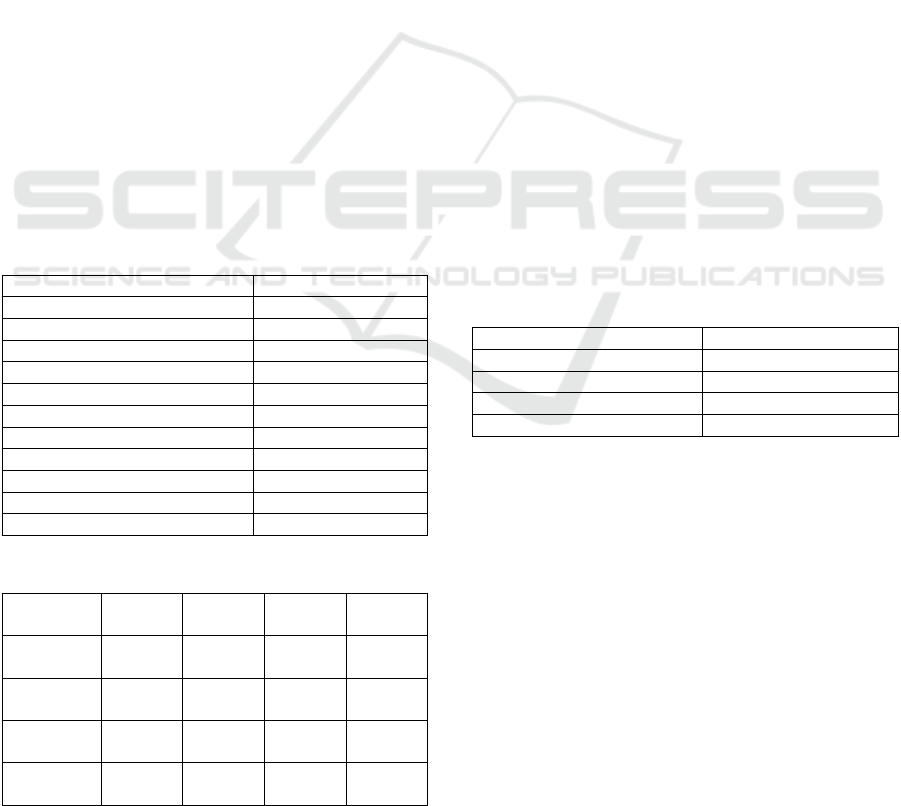
Table 1: The traditional purse seine boat characteristics.

Boat design parameters Dimension

Length of Perpendicular (Lpp) 13.1 m

Breadth 4.15 m

Draft 1.56 m

Height 1.97 m

Block Coefficient 0.53

Service speed 9 knot

Total Resistance 15.18 kN

Wake Fraction 0.15

Number of propeller Single Screw

Height of propeller aperture 1.20 m

Thrust deduction 0.12

Table 2: Propeller data specification.

Design

Parameters

3-Bladed 4-Bladed 5-Bladed 6-Bladed

Propeller

Diam. (D)

0.90 m 0.90 m 0.90 m 0.90 m

Area Ratio

(AE/A0)

0.35 0.56 0.62 0.74

Pitch Ratio

(P/D)

1.0 1.0 1.0 1.0

Advanced

Coeff. (J)

1.281 1.340 1.353 1.347

3 MATERIALS AND METHODS

In this research work the developed B-series propeller

for traditional purse seine boat are studied with the

boat characteristics and the propeller specifications

data as can be seen in the Table 1 and Table 2,

respectively. The objective of this study is to

investigate the structure response of the developed B-

series propeller of the traditional pursed seine boat in

the North Coastal Region in Central Java.

3.1 Material of the GFRP Propeller

The glass fibre reinforced plastic (GFRP) materials

have been implemented in many products in the field

of marine engineering such as boat, turbine, outfitting

components and propellers. GFRP material has

offered high strength characteristics with the low

weight and better corrosion resistance.

In the numerical analysis of the investigation of the

structural response, the material of propeller was

defined as an isotropic material. Although the

composite material is should be represented as an

orthotropic, however, for the simplification of the

computational process, the isotropic is still reliable to

provide an accurate result for estimation of the

propeller structure behaviour. The mechanical

properties of the GFRP for propeller material is can

be found in Table 3.

Table 3: Mechanical properties of GFRP for the propeller

material.

Properties GFRP

Young Modulus, (E) 42.70 GPa

Poisson Ratio (ν) 0.30

Shear Modulus (G) 5.10 GPa

Density (ρ) 1800.00 kg/m

3.2 Finite Element Model and

Simulation

The finite element model was defined as

representation of the B-series propeller. In order to

define the pressure load on the propeller blade, the

flow simulation should be made using CFD analysis.

The CFD model was considered as a cylindrical

domain. The inlet and outlet was defined as an

upstream and downstream, respectively. The

unstructured grid was adopted for the model

computation. The propeller model is represented by

the solid element which is located on the centre of the

origin axis in the coordinate system. The CFD model

is can be seen on the Fig.1.

ISOCEEN 2018 - 6th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management

150

Figure 1: CFD simulation model: Size of domain (left),

Unstructured grid mesh model (right).

Since the pressure distribution is obtained as the

result of the CFD analysis, the propeller blade FE

model is defined with the pressure results. The

pressure load is defined on the face of blade surface

and the back of blade surface. The detail of CFD

analysis to determine the pressure load can be found

in the previous study, (A. Windyandari, G. D.

Haryadi, and A. F. Zakki, 2018). The FE model of the

B-series propellers can be seen in the Fig. 2. The

meshing process was made using the auto mesh tools

of the software application. The entire solid elements

was modelled using 3D element which is 4 nodded

tetrahedrons mesh is adopted. The FE models of the

propellers consist of 198093 nodes, 1323641

elements for 3-bladed propeller; 1615082 nodes,

96463 elements for 4-bladed propeller; 198124

nodes, 118424 elements for 5-bladed propeller and

228001 nodes, 135632 elements for 6-bladed

propeller. The boundary condition of the simulation

was defined as fix support on the centre of the

propeller hub.

Figure 2: FE model of propellers: (a) 3-bladed;

(b) 4-bladed; (c) 5-bladed; (d) 6 bladed.

4 RESULTS AND DISCUSSIONS

The strength characteristics of the B-series propeller

for traditional purse seine in the North Coastal Region

of Central Java have been simulated. The numerical

simulation using FEM was conducted to observe the

essential parameters for the integrity of propeller

strength such as maximum deformation and stress

distribution which is represented as Von Mises Stress.

The results of the simulation are presented in Fig. 3

and Fig.4 for maximum deformation and Von Mises

stress distribution, respectively.

Figure 3: Maximum deformation of propellers:

(a) 3-bladed; (b) 4-bladed; (c) 5-bladed; (d) 6 bladed.

Figure 4: Stress distribution of propellers: (a) 3-bladed;

(b) 4-bladed; (c) 5-bladed; (d) 6 bladed.

The deformations of each propeller are 1.80 mm,

2.21mm, 2.50mm and 3.84 mm for 3-bladed

Strength Analysis of Glass Fibre Reinforced Plastics B-series Propeller for Traditional Purse Seine Boat in the North Coastal Region of

Central Java Indonesia

151

propeller, 4-bladed propeller, 5-bladed propeller and

6-bladed propeller, respectively, see Fig. 3.

According to the deformation results, it might be seen

that the maximum deformation is occurred on the 6-

blade propeller with the magnitude of deformation of

3.84 mm, see Fig. 3(d). The results can be explained

that the 6-bladed propeller which is able to produce

the largest thrust force have generated the largest

pressure load on the blade structure. Therefore the

generated pressure might influence the deformation

response of the propeller. The simulation results also

show that the larger blade numbers generally produce

a larger structure deformation response. The tendency

can be explained since the larger blade number was

produced the larger thrust force. This can be

identified that the larger generated thrust might

increase the hydrodynamic pressure on the blade

propeller.

The maximum stress of the propellers is obtained

on the connection between the blade and the hub of

the propeller, see Fig. 4. The stress distributions of

each propeller are 106 MPa, 120 MPa, 143 MPa and

174 MPa for 3 bladed propeller, 4-bladed propeller,

5-bladed propeller and 6-bladed propeller,

respectively. The stress distribution results have

shown the same tendency with the deformation

results that the larger blade number generates the

larger maximum stress on the propeller structure.

Therefore, it is also can be indicated that the

generated thrust of the propeller have an influenced

on the stress response of the blade propeller. Since the

properties of the GFRP material has the tensile

strength of 870 MPa, all of the propellers design is

reliable to support the propulsion system for the

traditional boat.

5 CONCLUSIONS

The study on the structural response of Glass Fibre

Reinforced Plastic B-series propellers for traditional

purse seine in the North Coastal Region of Central

Java was made. For determining the pressure load of

the propeller, the simulation of flow on the propeller

is conducted using CFD analysis. Subsequently the

pressure distribution results are defined as the load

condition on strength analysis using finite element

method.

According to FE analysis results, the maximum

deformation of 3.84 mm is obtained on the 6-bladed

propeller and the minimum deformation of 1.80 mm

is observed on the 3-bladed. It may be concluded that

the deformation of the propeller has enlarged while

the number of blade is increased. It can be explained

that the increase of propeller blade number could

generate the larger thrust force that may influence the

pressure on the blade. In the case of stress

distribution, the maximum stress of 174 MPa is

occurred on the 6-bladed propeller. The maximum

stress of the 6-bladed propeller is 64.15% larger than

3-bladed propeller. Although the 6-bladed propeller

have the largest maximum stress, however the entire

propeller design is accepted and reliable to be

implemented for the propulsion system of traditional

purse seine boat because the maximum stress is below

the tensile strength of GFRP material.

REFERENCES

A. Windyandari, G. D. Haryadi, A. F. Zakki, 2018.

Excellent Fundamental Research Report. unpublished.

A. Windyandari, H. Yudo, A. F. Zakki, 2018. ARPN

Journal of Eng. Appl. Scie. 13, 6.

D. W. Taylor, 1933. The speed and power of ships, Eansdell

Inc, Washington D. C.

H. Yudo, A. Windyandari, A. F. Zakki, 2017. IJCIET 8, 8.

J. E. Connolly, 1961. Trans. RINA 103.

J. H. McCarthy, 1969. NSIIDEC Report 3182.

J. P. Blasques, 2010. Mar. Struc. 23.

J.W. Cohen, 1955. Netherlands Res. Cen. T. N. O. Report

21S.

P. Atkinson, 1968. Trans. RINA 110.

R. J. Boswell, 1969. NSRDC Report 3247.

R. Wereldsma, 1965. Netherlands Res. Cen. T. N. O. Report

51M.

T. Sontvedt, 1974. Comp. & Struc. 4, (1974).

Y. Hong, 2017. Ocean Eng. 144.

Y. L. Young, 2007. Proc. 16th Conf. on Composite Mat.

Y. L. Young, J., 2008. Fluids & Struc. 24.

ISOCEEN 2018 - 6th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management

152