Effectiveness of The Jigsaw Strategy on Students Achievement in

Mathematical Statistics I Course

Hazmira Yozza

, Yudiantri Asdi

, and Izzati Rahmi HG

Department of Mathematics, Andalas University, Padang, Indonesia

Keywords: Mathematical Statistics, Cooperative Learning, Jigsaw, Learning Achievement.

Abstract: Mathematical Statistics I is a compulsory course for the 4th term students in the Mathematics Department,

Andalas University. The main problem faced in this course is the lack of students involvement which then

affects their academic achievement. This research is concerned about the effectiveness of the jigsaw strategy,

a cooperative learning approach, on the learning achievement of undergraduate students who took this course

in the academic year 2017/2018. The classroom action research was conducted in two cycles. By comparing

the final grade for the academic years 2016/2017 and 2017/2018 it was found that the jigsaw approach worked

successfully to enhance student’s learning achievement. It was also found that this strategy can increase

student’s involvement while improving teamwork and independence in the learning process and enhance

students’ understanding of the material being studied..

1 INTRODUCTION

At present, learning that makes lecturers as the center

of knowledge transfer is still a hallmark of learning in

universities. With this approach, the lecturer will

become a central figure in the transfer of knowledge

while students passively listen to lecturers and are not

too involved in the learning process they undergo. On

the other hand, the world of work requires university

graduates who not only have good hard skills but are

also able to think logically, analytically, critically and

creatively, are able to work in a team, have excellent

communication skills and other soft skills. As a result,

there is an imbalance between the competencies

possessed by university graduates and the expected

competencies in the world of work.

For this reason, a paradigm shift is needed in the

learning process from traditional learning to a

learning approach that can place students in the center

of the learning process, usually known as student-

centered learning. This learning strategy puts all

students as active and independent adult learners with

responsibility for their learning. With these

principles, a university graduate can be expected to

become a long-life learner with a balanced ability of

hard skills and soft skills. Meta-analysis shows that

various approaches of student-centered learning

effectively enhances students' academic achievement,

is more suitable in forming the attitudes that are

expected in the learning objectives and furthermore,

improve the retention of the lecture material being

studied (Afrizal et.al., 2014)

Mathematical Statistics I is a compulsory course

in the 4

term in the Department of Mathematics of

Andalas University. This course covers how to apply

mathematical principles to statistics and provides a

theoretical foundation for studying and developing

various statistical methods used to analyze data. At

present, most of the meetings in this course are

carried out using a teacher-centered learning

approach. With this approach, learning outcomes are

still not satisfactory, because more than 40% of

students fail or gain unsatisfactory grades.

Therefore, another learning approach is needed

that can enhance students’ learning outcome in this

course. One strategy that can be used is the jigsaw

strategy. This research aims to evaluate the impact of

using cooperative learning based on a jigsaw strategy

on students’ learning achievement in the

Mathematical Statistics I course.

At present, there is a paradigm shift in learning,

especially in higher education, from a teaching

paradigm to learning paradigm. With this new

paradigm, students are placed as a center in the

learning process. One type of student-centered

learning is cooperative learning. This learning

strategy is defined as an instructional method where

Yozza, H., Asdi, Y. and HG, I.

Effectiveness of The Jigsaw Strategy on Students Achievement in Mathematical Statistics I Course.

DOI: 10.5220/0008679000380043

In Improving Educational Quality Toward International Standard (ICED-QA 2018), pages 38-43

ISBN: 978-989-758-392-6

the students need to work collaboratively in small and

heterogeneous groups, helping each other to learn a

specific assignment to achieve a common goal

(Strother, 1990; Kagan, 1994). Compared to

individualistic learning, this approach is proven to

improve students' performance (Johnson and

Johnson, 1999; Slavin, 1999). To be effective; the

cooperative learning must be well-planned and

structured with learning materials available to all

participants (Azmin, 2015). There are several types of

cooperative learning. The Jigsaw strategy is one of

them.

Elliot Aroston originally introduced and used the

Jigsaw instructional procedure in 1971 in Austin,

Texas to help the students develop their social and

cooperative skills (Aronson and Bridgemen, 1979).

With this approach, the content of the lesson is

divided into several parts of information, just like in

jigsaw puzzle. The students are also divided into

several heterogenous groups consist of 5-6 students

refered to as the ‘jigsaw’ group, where they are each

given a specific subtopic. In the next step, students

break out of their jigsaw groups and form ‘expert’

groups, where they focus on one subtopic,

researching and discussing it and become experts on

the subtopic that they have been assigned to. Next, the

students return to their jigsaw groups and teach their

peers based on their discussions in the expert group.

Eventually, all the members of the jigsaw groups will

have learnt from each expert group discussion and

will have benefit from each other (Azmin, 2015). In

this method, the lecturer acts as a motivator,

facilitator and assesses students activities.

2 METHOD

The classroom action research conducted this study.

Learning strategy used a combination of a Teacher-

Centered Learning (TCL) approach and cooperative

learning using a jigsaw strategy.

2.1 Population and Participants

The population of this study was all students who

took Mathematical Statistics I in the academic year

2017/2018. The students were grouped into three

classes labeled A, B and C, consisting of 33, 34 and

30 students respectively. All members of the

population participated in this study.

2.2 Study Design

This classroom action research was carried out during

the even semester of the academic year 2017/2018.

This research was done in two cycles, each cycle

consisting of 4 steps, as follows:

Step 1: Planning. At this stage, a strategy was

designed to achieve the learning objectives,

starting from identifying the problems that

arose in the learning process of the

Mathematics Statistics I course, analyzing

the causes and then developing an action

plan through the development of the

Semester Learning Plan and students’

worksheets for lectures and tutorials. In this

activity, an indicator of the success of the

action was also determined. This step was

conducted through week 1-5.

Step 2: Implementation. At this stage, actions that

had been planned were implemented. The

chosen Jigsaw strategy was used. This

strategy was applied to two specific topics

(a) The Properties of Expectation Values, (b)

Special Discrete Distribution and also

applied to the tutorial class. This step was

conducted through week 6-10.

Step 3: Observation. At this stage, observations

were carried out to identify events

encountered in the implementation of the

action, which included obstacles

encountered and activities carried out by

students during the learning process. This

activity was conducted in conjunction with

the implementation step.

Step 4: Reflection. The last stage of this research was

the evaluation of the results of actions taken

based on predetermined indicators.

2.3 Data Collection and Analysis

Data were collected during the implementation step.

The collected data were the scores of the exams,

quizzes and students' perceptions of the effect of this

learning method on the active involvement of

students, motivation to learn material independently

and teamwork improvement. The measurement of

students’ opinion was carried out by distributing

questionnaires to all students. The questionnaire used

a Likert scale. Data were analyzed using descriptive

statistics (central tendency and variability measures)

as well as statistical tables and graphs.

Effectiveness of The Jigsaw Strategy on Students Achievement in Mathematical Statistics I Course

2.4 Performance Indicator

Indicators used to assess the success of teaching

methods, and assessments developed in this

Classroom Action Research activity were:

Learning Outcomes. Learning outcomes were

measured from assignments, quizzes and exams.

Distribution of students’ final grade. The criteria for

success was the percentage of students who get a

score below B is lower than the previous academic

year. Students’ opinion of the learning method was

measured from a questionaire. The criteria for success

was more than 75% of the students expressed a

positive opinion of this learning method.

3 RESULTS AND DISCUSSION

Here we will describe the development of the learning

and assessment method as a solution to problems

faced in Mathematical Statistics I learning process.

We will also discuss the result of the action done.

3.1 Development of The Learning

Method

In the previous academic year, the learning process of

Mathematics Statistics I courses was carried out by

combining the TCL, and SCL approaches with the

Think Pair and Share (TPS) method. From the

evaluation, this method was not sufficient to actively

involve all students in the learning process. In

addition, the large number of students made it

difficult for lecturers to assess the activity of all

students. Besides, the tutorial activities did not

provide enough opportunities for all students to be

active in learning activities.

From the learning outcomes of previous years, it

was suspected that the learning outcomes of students

in this course were related to their activeness in the

learning process. Students who got good grades were

generally students who participated actively in the

learning process. Therefore, it was seen advantageous

to improve the learning methods to encourage all

students to particpate actively to further improve the

quality of students learning outcomes.

The TCL and TPS methods were still used to

ensure that all material could be completed in 14

weeks of class meetings. Also, quite a lot of material

is not easy to present in other ways. Learning methods

were developed for the part of the course most

suitable for the Cooperative Learning method using

Jigsaw Strategy: “Properties of Expected Value” and

“Special Discrete Distributions”.

The procedure performed is as described

previously. The basis of the group division was the

students’ grade in Elementary Statistics, Calculus I

and Calculus II courses. A modification was made by

appointing one student from each group as a leader.

He/she was responsible for learning all the material

that would be discussed and to lead the discussion.

Ideally, this student must have good academic

abilities and be the most mature in the group. Thus,

if students have difficulty explaining the parts they

are responsible for, this leader can help him.

Furthermore, several students were appointed by the

lecturer to explain or rewrite the results of the

discussion for all participants of the course while

other students responded or asked questions about the

presentation or answer given. In this approach, the

lecturer only acts as a motivator, facilitator and

assesses the course of the discussion. The jigsaw

strategy was also applied in tutorial activities.

3.2 Development of Student Assessment

Strategy

The assessment carried out in this course included

results-assessment and process-assessment. The

results-assessment was measured through 3 Exams

and Quizzes while the process assessment was

measured through assignments, tutorials and group

discussions conducted using the jigsaw approach.

Performance indicators were: logical, analytical and

critical thinking skills; creativity, time management,

teamwork and communication skills.

3.3 Development of The Semester

Learning Plan

Furthermore, improvements were made to The

Semester Learning Plan (SLP) of the Mathematics

Statistics I course. Improvements were mainly made

on the learning approach used, where the jigsaw

strategy was applied to several topics. In addition, the

assessment method was also proscribed in more

detail. This SLP was also supplemented with a class

discussion worksheet which was used as a guide to

carrying out class discussions.

3.4 Result of The Classroom Action

Research and Discussion

This Classroom Action Research was carried out in

two cycles. The following will describe the actions

and results of each cycle.

ICED-QA 2018 - International Conference On Education Development And Quality Assurance

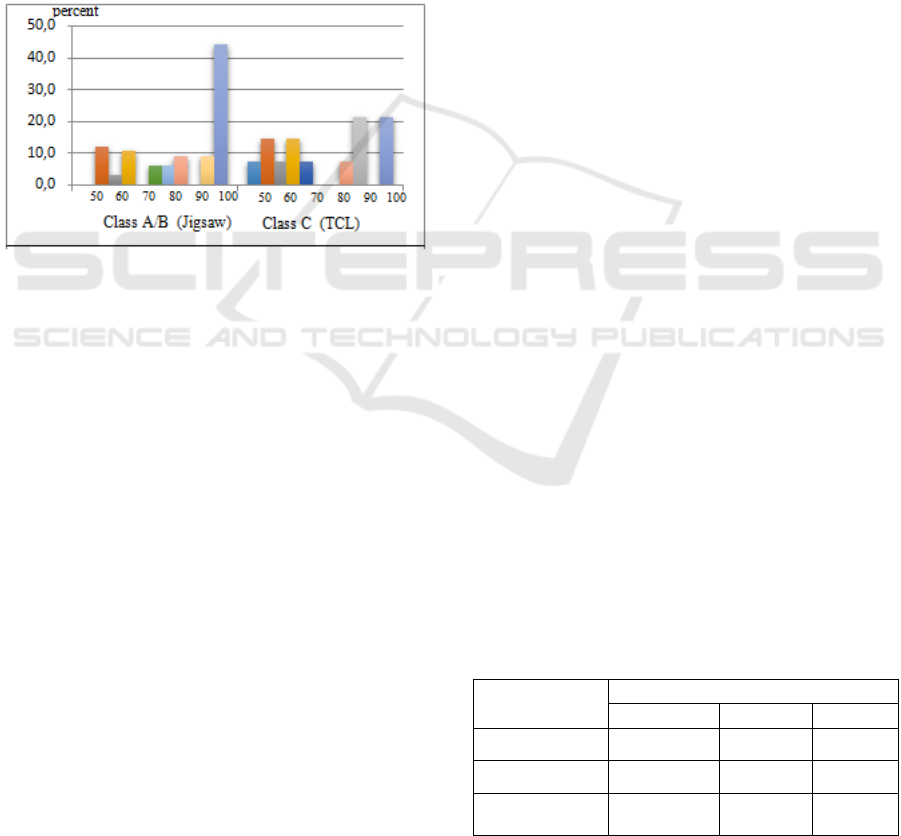
3.4.1 Cycle-1

In this cycle, a jigsaw strategy was applied to lecture

activities on topics of ‘Properties of Expectation

Values’ and ‘Special Discrete’ Distribution. For the

first topic, the jigsaw approach was only applied to

students in Class A and B, while class C still used the

TCL approach. Evaluation of learning outcomes was

measured in the form of a quiz. For Classes A and B,

the average score was 81.5 with a standard deviation

of 18.24 and for class C, the average was lower,

namely 73.18 with a more substantial standard

deviation of 19.18. Comparison of the distribution of

student quiz scores between students in Class A/B

and students in class C is shown in the following

figure.

Figure 1: Comparison of Quiz 1 Distribution

It can be seen that the distribution of grades of A

and B students (Jigsaw) is more encouraging than the

distribution of students’ grades in Class C (TCL).

Nearly 50% of students in Class A / B scored grades

95 - 100 and only about 30% of students scored less

than 75. Meanwhile, in class C only about 20% of

students scored grades at 95-100 and 50 % of students

scored below 75.

For the Special Discrete Distribution topic, the

jigsaw strategy was applied to all classes. Assessment

of learning outcomes was measured from the results

of a second quiz, and the average score was 64.73

with a standard deviation of 22.27. The number of

students scoring above 70 is quite significant, namely

42% of all students. However, this result is still

unsatisfactory, because 30% of the students scored

below 50.

The evaluation of the effect of this jigsaw strategy

on student involvement in the learning process shows

that this approach can increase the percentage of

students who are actively involved in the learning

process but is still not completely effective because

there were many students who remained uninvolved

in the learning process.

Several things might be the cause of this, namely:

 Lack of preparation. As with other SCL

strategies, with this jigsaw approach, all

students must study the discussed material

before class. However, it was found the

students did not prepare themselves well as

might be expected. This might be because

the course in Mathematics Statistics is

theoretical and requires understanding of

many new basic concepts and terms.

 Incompetent leaders.

3.4.2 Cycle-2

This cycle was done because the results obtained in

the cycle -1 were unsatisfactory. Some of the method

improvements made in this second cycle were:

1. The jigsaw strategy was applied to the tutorial

activities. From experience, students are more

enthusiastic about the completion of the exercise

which they have learned about beforehand.

2. Change of some leaders who were considered to

be less competent.

3. Motivation of students to learn the material.

Learning outcomes with the Jigsaw approach

conducted in this tutorial activity can be seen from the

grades in quiz 3. The results obtained are better than

before with a higher average (66.20) and a lower

standard deviation (16.03).

Another indicator is the active involvement of

students in the lecture/tutorial activities. Table 1

illustrates the comparison of student involvement in

learning that uses the TCL approach, jigsaw strategies

on lecture activities and jigsaw strategies in tutorial

activities.

Table 1 shows that the application of jigsaw

strategies in this course is effective in increasing

student involvement in lectures and tutorials

activities. For tutorial activities, the application of this

jigsaw method can involve almost all students

actively in the learning process. This may be because

the materials discussed were questions or exercises

related to the material they had learned about

beforehand in the lecture.

Table 1: Student Involvement

Learning

Strategy

Student Involvement (%)

Active

Moderate

Passive

TCL

Jigsaw – class

Jigsaw –

tutorial

Effectiveness of The Jigsaw Strategy on Students Achievement in Mathematical Statistics I Course

From the table, it can be seen that the application of

jigsaw strategies in this course was effective in

increasing student involvement in lectures and

tutorials activities. For tutorial activities, the

application of this jigsaw method can involve almost

all students actively in the learning process. This is

thought to be due to the material related to the

questions having been previously learnt in the

lectures.

3.4.3 The final grade distribution

The student's final score is in the 0-100 range and is

calculated based on the results- assessment and

process-assessment. Furthermore, the academic grade

for this course is based on the final score.

Fig. 2 shows a comparison of the academic grade

distribution in the academic year 2016/2017 (using

the TCL approach) and the academic year 2017/2018

(using the jigsaw approach).

Figure 2: Comparison of final grade distribution

The distribution of student grades in these two

academic years is right-skewed which means a larger

number of higher scores. The distribution of students

grades in the academic year 2017/2018 shows a

higher percentage students have higher marks than

the previous year with a higher percentage of A, A-

and B + and a lower percentage of E, D and C values.

In this academic year, there were no students who

received E grades and only 3% of students received a

D. The percentage of students who received grade B-

or less also decreased from 42% to 33%.

3.4.4 Students’ opinion of the jigsaw

strategy:

The student's opinions toward the learning method

conducted was collected by distributing

questionnaires at the final meeting. In the

questionnaire, students were asked to state the degree

of approval of several statements related to the

application of this jigsaw method. The degree of

approval is expressed using a Likert scale (1 =

strongly disagrees, 2=disagree, 3 = moderate,

4=agree, 5= strongly agree). Fig. 3 shows the average

students’ opinion scores in several areas.

Figure 3: Likert scale scores from student feedback on the

Jigsaw method's success in several areas

Fig, 3 shows that the students had positive

opinions about the implementation of this jigsaw

method. Students considered that this approach could

create a fun learning atmosphere, increase student

involvement in the learning process, increase team

collaboration and enhance students' understanding of

the material discussed. This method was generally

considered helpful to motivate students to learn the

material to be discussed before the discussion takes

place.

Also, the students were also asked for their

opinions about what activities this jigsaw method

should be applied to. Almost all students wanted this

approach to be applied in tutorial activities and part

of lecture activities. Only about 4% of students

preferred the TCL method to be fully implemented in

all lecture activities.

4 CONCLUSION

In this study, classroom action research was

conducted to determine the effect of a Cooperative

Learning Method using a Jigsaw Strategy on student

learning outcomes in Mathematics Statistics I. This

study concluded that the jigsaw method is an effective

approach to improve student learning outcomes and

resulted in fewer students failing this course. In

addition, students considered that this approach

provided a fun learning atmosphere, was able to

increase student involvement, enhance student

understanding, improve teamwork and motivate

ICED-QA 2018 - International Conference On Education Development And Quality Assurance

students to learn the material themselves before the

class activity took place.

ACKNOWLEDGMENT

This classroom action research was funded by

Institute of Educational Development and Quality

Assurance, Andalas University. On this occasion, we

are grateful for the opportunity and funds that have

been provided to make this research possible.

REFERENCES

Afrizal, Safni, Mansyudin, H. Lucida, A. Pratoto, N. A.

Syah, D.T. Iman, Maizufri, D. Hellard, M. E. Mahata.

2014. Panduan praktis pelaksanaan student-centered

learning. Padang: Andalas University.

Aronson, E., & Bridgeman, D. L., 1979. Jigsaw groups and

the desegregated classroom: In pursuit of common

goals. Personality and Social Psychology Bulletin, 5(4),

438-466.

Strother, D. B. 1990. “Cooperative learning : fad or

foundation for learning,” Phi Delta Kappan, vol. 72,

pp.158-162.

Kagan, S. 1994. Cooperative Learning. San Celemente,

California: Kagan Publishing.

Johnson, D.W. & R.T. Johnson, “Making cooperative

learning work,” Theory into Practice, 1999, vol. 38(2),

pp. 67-73.

Slavin, R. “Research on cooperative learning and

achievement : What we know, what we need to know,”

Conteporary Educational Psychology, 1999, Vol. 21,

pp. 43-69.

Azmin, N.H. 2015. “Effect of the jigsaw-based cooperative

learning method on student performance in general

certificate of education advanced-level psychology : An

Exploratory Brunei Case Study,” International

Educational Studies, vol. 9(1), pp. 91-106.

Effectiveness of The Jigsaw Strategy on Students Achievement in Mathematical Statistics I Course