
Increased Assessment for Discrete Mathematics Course with Small
Group Discussion
Des Welyyanti
and Narwen
Faculty of Mathematics and Natural Sciences, Universitas Andalas, Padang, Indonesia
Keywords: Student Centered Learning, Assessment, Small Group Discussion.
Abstract: Student Centered Learning is a learning method whereby students are the center the learning process. It means
that students must be active in the learning process under the lecturer’s supervision. One of the Student
Centered Learning methods is Small Group Discussion. Small Group Discussion is a discussion method
consisting of 3-4 students. In each group, every student actively discuss the subject. This paper determines
the increased assessment for Discrete Mathematics course which uses Small Group Discussion as a learning
method.
1 INTRODUCTION
Discrete Mathematics is a course given to
mathematics students of level II (two) in the fourth
semester. This Discrete Mathematics is one of the
compulsory subjects which are part of the field of
study in combinatorial Mathematics interests.
Students can take this course if they have taken the
Introduction to Mathematics course which is a
prerequisite for Discrete Mathematics courses. In
addition, Discrete Mathematics courses also relates to
one of the subjects in the field of combinatorial
Mathematics interest studies, namely the Number
Theory course. Introduction to Mathematics and
Number Theory courses are given to mathematics
students of the first level, namely in the first and
second semester.
In Discrete Mathematics, the emphasis is on
understanding the logic of proof and some basic
principles of proof in mathematics (Robert, 2001).
After taking this course, students are expected to be
able to think logically, systematically and structurally
in reasoning and solving a problem in the field of
mathematics (Meng et.al., 2018; Garcia et.al., 2011).
The learning objectives of Discrete Mathematics
are to allow students to build strong understanding of
logic and ways of proof, use the principle of
mathematical induction, understand the basic
principles of counting, the principle of nesting
pigeons, permutations and combinations, binomial
coefficients, basic concepts in discrete opportunities,
recurrent relations, generating functions, the principle
of inclusion-exclusion and the concept of relation.
Furthermore, the learning outcomes of Discrete
Mathematics are:
Students are expected to be able to:
a. Construct evidence inductively.
b. Understand the basic principles of
mathematical induction and some proof
techniques, and apply them to relevant cases.
c. Identify the relationship between problems in
discrete mathematics with other branches of
mathematics and science.
d. Have critical, analytical and innovative
thinking to reason logically and structurally.
e. Communicate their thoughts systematically,
work together and adapt with other students in
the group, and conduct good discussions.
The contribution of Discrete Mathematics for the
learning achievement of the Mathematics study
program is that students have a strong understanding
of logic and way of proof. They master the basic
principles of mathematical induction and some
verification techniques and can apply them to relevant
cases, and understand the basic principles of counting
(Robert, 2001; Kularbphettong, 2015).
The teaching materials that have been used in
Discrete Mathematics are presentation slides made
with Microsoft power point and a textbook in the
form of handouts. Furthermore, the learning method
that is commonly applied to discrete courses is
Teacher Centered Learning (TCL), which means that
Welyyanti, D. and Narwen, .
Increased Assessment for Discrete Mathematics Course with Small Group Discussion.
DOI: 10.5220/0008680500970100
In Improving Educational Quality Toward International Standard (ICED-QA 2018), pages 97-100
ISBN: 978-989-758-392-6
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
97
classroom learning is centered on the lecturer as a
source of learning material.
The Following is the assessments made so far.
Assessment criteria consist of evaluating results and
processes:
Table 1: Component of Assessment.
No
Component Assessment
Weight (%)
Assessment of Results
1
Midterm Examination
30 %
2
Final Examination
30 %
3
Quiz
20 %
4
Excersises+Home Work
20 %
TOTAL
100 %
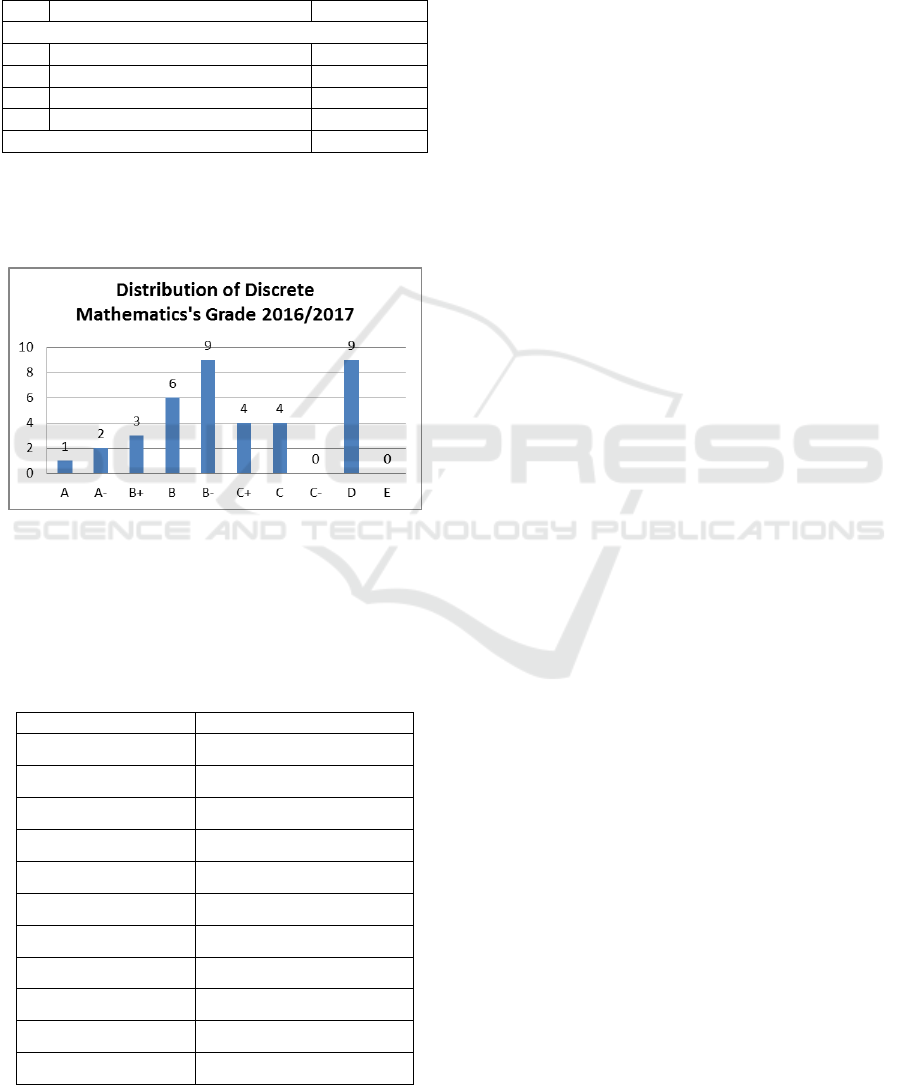
Furthermore, the distribution of the final grades of
Discrete Mathematics courses for Class B in the
academic year of 2016/2017 is as follows:
Figure 1: Distribution of Discrete mathematics’s Grade
2016/2017.
From the Distribution, the above values are obtained
as follows:
Table 2: Final grades of Discrete Mathematics courses for
Class B in the academic year of 2016/2017.
The problem that arises during this time is the low
learning ability of students in working the exercises
given. Exercises can be work done either at home or
in class during in the lecture.
2 RESEARCH METHODOLOGY
This research was conducted in the classroom within
one semester, namely even semester in the academic
years 2017/2018 and involves students in Discrete
Mathematics courses (courses in the fourth semester).
The research stages are as follows.
2.1 Research Design
The method that will be carried out in the Classroom
Action Research in Discrete Mathematics in Class B
for the academic years of 2017/2018 is Small Group
Discussion method. In this method, the lecturer will
form small groups consisting of three or four students
(Eden, 2005).
Before discussing a subject or an exercises, the
lecturer explains in advance the related subject.
Furthermore, students will be given individual
assignments done at home. The task is related to the
subject or exercises that will be discussed in the group
in the next meeting. Every student must be able to
explain and discuss the material or training in the
group that has been formed. At the end of the
discussion, the lecturer will randomly appoint
students who will explain the results of the group
discussion. It means that each student must be able to
explain what has been discussed in the group. If there
are students who cannot explain the results of the
group discussion, the group scores will be reduced.
Student’s understanding and activeness in the
discussions held are assessed. This is is a group
assessment not an individual assessment. It means
that each student must be responsible for what has
been discussed in the group. Assessment is also done
by giving individual assignments, quizzes, Midterm
Examinations, and Final Examinations.
For evaluation, students respond to development
learning methods are carried out by asking students
for suggestions and criticisms of the learning method
that has been done for one semester.
2.2 Limitation of Research
The limitation of this research is the effect of Student
Centered Learning (SCL) methods on assessment of
Discrete Mathematics courses, especially small group
discussion method. The subjects of this study are
Final Grade
Number of Students
A
1
A-
2
B+
3
B
6
B-
9
C+
4
C
4
C-
0
D
9
E
0
Number of Students
38
ICED-QA 2018 - International Conference On Education Development And Quality Assurance
98

students who took the Discrete Mathematics course
for the Academic Year 2017/2018. Especially
students in the fourth level or students who repeated
discrete mathematics in class B.
2.3 Data Analysis and Collecting
Methods
This method consists of collecting the values obtained
from students who take Discrete Mathematics in the
Academic Year 2017/ 2018. These values are
personal assignments, group assignments, quizzes,
Midterm and Final Examinations. Furthermore, this
these values will be compared with the values of
students who took the Discrete Mathematics course in
the Academic Year 2016/2017.
3 RESULTS AND DISCUSSION
Classroom Action Research that has been carried out
is applying SCL (Student Centered Learning)
Method. SCL Method is a method whereby students
are required to understand the subject under the
guidance of the lecturer. The SCL Method applied in
this research is the Small Group Discussion method.
Classroom Action Research conducted has several
parameters.
3.1 The Results of Student Learning
Achievements
Students’ activities and understanding during
learning or discussion becomes one of the parameters
of the results of the learning outcomes. In addition,
independent assignments, Midterm and Final
Examinations are also used as parameters for learning
outcomes. In Classroom Action Research, the
activeness and understanding of students at the time
of learning increased compared to those of students in
the previous school year. It is directly proportional to
the assessment of students in independent
assignments, questions about Midterm and Final
Examinations.
The distribution of students’ final grades at the
end of learning is also a parameter in this Classroom
Action Research. In Classroom Action Research, we
get an increase in the distribution of students’ final
grades. The final distribution of Discrete
Mathematics courses for Class B in the academic year
2016/2017.
Furthermore, distribution of the final grades of the
Discrete Mathematics course for Class B of the
academic year 2017/2018 is as follows:
Figure 2: Distribution of Discrete Mathematics’s Grades in
2017/2018.
From the above distribution values are obtained are
as follows:
Table 3: Final grades of Discrete Mathematics courses for
Class B in the academic year 2016/2017.
Final Value
Number of Students
A
2
A-
4
B+
4
B
7
B-
4
C+
6
C
4
C-
0
D
0
E
0
Number of Students
31
On both distributions, the value of students in
Discrete Mathematics of Class B increased in the
Academic Year 2017/2018. In Discrete Mathematics
of Class B of the Academic Year 2017/2018, there
were no students with a final grade D. Meanwhile, in
the Academic Year 2016/2017, there were nine
students with a final grade D. Then, at the final exam,
there is also an increase in the number of students in
Discrete Mathematics courses of Class B in the
Academic Year 2017/2018. Students with final
grades A, A-, B+ and B were as many as two, four,
four and seven students respectively. Meanwhile, in
the Academic Year 2016/2017 there was one student
with a final grade A, two students with a final grade
Increased Assessment for Discrete Mathematics Course with Small Group Discussion
99

A-, three students with a final grade B +, and six
students with a final grade B.
3.2 Student Response
Student Responded to the development of learning
methods by asking for suggestions and criticism on
the learning method that has been done for one
semester. In the middle of the semester and the end of
the semester, students were asked to give suggestions
and criticisms on the learning methods carried out. It
is an evaluation for lecturers in the learning method
that is carried out during one semester.
4 CONCLUSION
In the Class Action Research, it was found that
students’ understanding of Discrete Mathematics
became has a significantly increased after using SCL
(Student Centered Learning) Methods, especially
Small Group Discussion.
REFERENCES
Eden, Colin, and Fran Ackermann, Theory into practice,
practice to theory: Action research in method
development. European Journal of Operational
Research, Volume 271, Issue 3, 2018, Pages 1145-
1155, https://doi.org/10.1016/j.ejor.2018.05.061.
Meng, J., J. Huang, S.W. Sloan, D. Sheng. Discrete
modelling jointed rock slopes using mathematical
programming methods. Computers and Geotechnics,
Volume 96, 2018, Pages 189-202,
https://doi.org/10.1016/j.compgeo.2017.11.002.
García, I,. L. Jódar, P. Merello, F.-J. Santonja. A discrete
mathematical model for addictive buying: Predicting
the affected population evolution. Mathematical and
Computer Modelling, Volume 54, Issues 7–8, 2011,
Pages 1634-1637,
https://doi.org/10.1016/j.mcm.2010.12.012.
Kularbphettong, Kunyanuth, Rungnapa Putglan, Nisnart
Tachpetpaiboon, Chollticha Tongsiri, Pattarapan
Roonrakwit. Developing of mLearning for Discrete
Mathematics Based on Android Platform. Procedia -
Social and Behavioral Sciences, Volume 197, 2015,
Pages 793-796, https://doi.org/10.1016/j.sbspro.2015.
07.184.
Roberts, F.S. Discrete Mathematics. Editor(s): Neil J.
Smelser, Paul B. Baltes, International Encyclopedia of
the Social & Behavioral Sciences, Pergamon, 2001,
Pages 3743-3746, https://doi.org/10.1016/B0-08-
043076-7/00602-1.
ICED-QA 2018 - International Conference On Education Development And Quality Assurance
100
