Wave Analysisi in near Shoreline for Coastal Morphology in Mouth

of Kali Porong Sidoarjo

Mahmud Mustain, Abdul Holil Situmorang, Suntoyo and Sujantoko

Department of Ocean Engineering FTK, Instititute Technology of Sepuluh Nopember (ITS) Surabaya, Indonesia

Keywords: Wave Analysis, Kali Porong, Shoreline.

Abstract: The wave is one of the important parameters in the dynamics of seawaters. Waves can cause energy to form

the beach, sorting sediments, causing the flow and transport of material sediments (sediment transport). This

research was conducted to find out the characteristics of the waveform that occurs around the mouth of Kali

Porong. This study uses data from the meteorological station of Cape Wind Silver during the period of 5 years

from the year 2011 – 2015 with the fetch direction of the dominant East. The calculation of the length of the

fetch effectively amounted to 161968.65 meter with the significant wave height H1/3 and (significant wave

period) T1/3 is 1.26 meters and 7.35 seconds. As for looking for refraction, shoaling and the surge broke the

researcher looking for using three slices that represent characteristics of an existing wave on site research. In

this research obtained for Slice 1 high waves broke 1.5459 meters with a depth of wave broke of 1.8989 m,

Slice 2 high waves broke 1.5458 meters with a depth of wave broke of 1.9181 m, Slice 3 high waves broke

1.5458 meters with a depth of wave burst of 1.9578 m.

1 INTRODUCTION

The Kali Porong (Porong River) canal is one of the

Brantas River in Mojokerto, flows eastward and

empties in the Madura Strait. Figure 1 shows

Location Study of the Coast around the Mouth of the

Kali Porong. The River is limiting Sidoarjo Regency

Pasuruan. This River is the river an artificial Canal

used aliases to redirect a portion of the flow of the

Brantas River that empties in Surabaya. Kali Porong

has two streams namely River Sedati (KP. 100) with

DAS of 406.7 Km2 and River Kambing (KP. 148)

with DAS of 196.6 Km2. The basic conditions are an

irregular river without large stones and shrub. The

natural geology of the Valley River Porong contains

volcanic rocks such as the piedmonte grumosol,

latosol, mediteran and alluvial. In November 2006,

the Government set Sidoarjo mud caused by Porong

Mud disaster in May 2006 is thrown through River

Porong to be streamed to the sea in the Madura Strait.

This has to be one of the causes of the occurrence of

a change of the coastline around the mouth of the

porong times (Mustain, et.al, 2010, 2017, 2018).

In addition to the extra mud from the river one of

the factors that also affect very large changes in the

coastline that is ocean waves. Waves can be caused

by energy to form the beach, sorting sediments,

causing the flow and transport of material sediments

(sediment transport) base towards the shore, offshore,

and along the coast as well as cause the forces acting

on the building of the coast. So the wave data is

indispensable in planning coastal buildings (such as a

jetty, of Groin, seawall, breakwater, reclamation etc.),

determining the layout of the Harbour, cruise and

flow management of the marine environment, and

marine and recreation area determination aquaculture

in the coastal area (Sugianto, 2010). Because of the

importance of the wave data for coastal structure

planning and coastal changes to the feature, then this

research needs to be done to find out the

characteristics of the wave itself. Characteristics of

waves that will be searched in this study i.e. the

refraction of waves and wave shoaling which broke

out. Therefore, the data from the study can be used

for further research needs in order to improve the

development and to estimate the possible happens in

the beach area.

Mustain, M., Situmorang, A., Suntoyo, . and Sujantoko, .

Wave Analysisi in near Shoreline for Coastal Morphology in Mouth of Kali Porong Sidoarjo.

DOI: 10.5220/0008767201890194

In Proceedings of the 6th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management (ISOCEEN 2018), pages 189-194

ISBN: 978-989-758-455-8

189

Figure 1: Location Study of the Coast around the Mouth of

the River Porong (Google earth, 2018).

2 THEORITICAL BACKROUND

2.1 Wind Driven Wave

The ripples on the surface water will be generating by

wind driven forces. The bigger of wind blowing will

produce the bigger and the longer of the ripples as

well. For the continuous of the wind, blowing the

ripples will become the wave. The high and the wave

period will depend on the wind velocity (U), time

blowing (t), and length of Fetch (F). The length of

Fetch need the long enough distance due to enough

energy from the wind to drive then to transfer to the

water to become the wave. Fetch formulation have

been given by Triatmojo (1999):

eff



cos





(1)

where:

Feff = Fetch effective

Xi = Length of fetch

αi = Deviation on either side of the wind direction

Using the angles added up to, 6o to 42o on both side

of wind direction, then the wave parameters could be

calculated by deep-sea wave forecasting formulas:

𝐻



 5.112 𝑥 10



𝑥 𝑈𝑎 𝑥 𝐹



.

(2)

𝑇



 6.238 𝑥 10



𝑥 𝐹_𝑒𝑓𝑓^2/𝑈𝐴





(3)

Where UA is the wind stress factor. These wave

parameters could be used to determine the Hrms,

Trms, H01/3, and T01/3 using the formulation below;





irms

(4)

𝐻

/

 1.416 𝑥 𝐻



(5)





irms

(6)

𝑇

/

1.42𝑥 𝑇



(7)

2.2 Refraction and Shoaling Waves

To calculate the refraction wave we could use the

formulation from the illustration of orthogonal wave.

Figure 2 illustrates the orthogonal wave. These

formulations are based on the fluxed conservation.

There are;

𝑃0𝑃𝐶𝑜𝑛𝑠𝑡𝑎𝑛𝑡

𝑛0 𝐵0 𝐸0 𝐶0  𝑛 𝐵 𝐸 𝐶

(8)

Where:

𝐸  𝑤𝑎𝑣𝑒 𝑒𝑛𝑒𝑟𝑔𝑦 𝐸 

𝜌 𝑔 𝐻





(9)

5.0;

2sinh

15.0















 n

(10)

Then we could write;

nBC

5.0





(11)



(12)

Where;

H0 = height wave in deep sea

H = height wave in site area

L0 = length wave in deep sea

L = length wave in site area

B0 = wide of orthogonal wave in deep sea

B = wide of orthogonal wave in site area

Ks = Shoaling coefficient

Kr = Refraction coefficient

2.3 Breaking Wave

The change of bathymetry near shoreline from the

offshore direction, normally create the slope so

ISOCEEN 2018 - 6th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management

190

steeply to the shoreline. This will change the wave

properties due to this slope, the wavelength become

shorter then, before and wave high so become higher.

The ratio between high wave to the length wave is

called by wave steepness. The reduction of wave

steepness is automatically will reduce the wave

stability. When the wave stability become lest then

the minimum, then the wave will automatically break.

This case normally is called the breaking wave. The

wave stability has the formulation (CERC, 1984) of:















LeH



tanh095.0

max

(13)

edH

5.3

max

65.0

(14)

Where;

Hmax = the maximum wave height before breaking

(m)

Lb = the wave length when breaking wave in site

location (m)

Db = the depth of the position of breaking wave in

site location (m)

3 DATA COLLECTION

3.1 Bathymetry

Bathymetries map data required to perform the

analysis of refraction, shoaling and changing

coastline. For the analysis of refraction, existing

bathymetries map was divided into several slices,

then to calculate coefficients of refraction and the

characteristics of the breaking wave. As for the

analysis of the changes of coastline, the existing map

first divided into a smaller number of slices. Then

done the measurements to get the initial Y-value (the

distance from the zero point to the shorelines early).

Next, the initial Y-results used in the calculation to

get the Y-end in every step of the time to illustrate the

changes in the coastline at the site of the study.

3.2 Wind

Wind data used in this research is the wind data from

the meteorological station of Tanjung Perak during a

period of 5 years from the year 2011 – 2015. Wind

direction will be stated in the form of eight parts of

the wind direction with the speed in knots. Before the

wind data logging results using WRPLOT, first data

is stored in the form of excel with the first column

containing format date data. The second column

contains the Moon, the third column contains the

year, fourth column contains, and then the fifth and

sixth column contains the direction and speed of the

wind. After that, wind data will be processed using

the program WRPLOT to get the dominant wind

direction and the number of occurrences of the wind

according to the direction and phase.

3.3 Wave

Wave data is necessary to know the quantity and

behaviour of waves heading toward the beach. Wave

data is used based on the conversion of wind data on

surface and land near the location of the research.

In the propagation of a wave to the beach, the waves

undergo a process of change in characteristics such as

height wave and long wave from Pratikto (1996).

Winds that blow across the surface cause disruption

on the surface of the water, the ripples with the

appearance of small waves on the surface of the

water. When the wind speed increases, the ripple will

be even greater when the wind blows continuously

then it will be making waves.

Characteristics of waves include form, height and

period of a wave that is formed depends on the

influence of wind speed (U), wind gusts (t), the length

of the fetch (F), as well as the direction of the wind.

Fetch can be defined as the length of the wave

generation area in the direction of the oncoming wind,

generally limited by the land surrounding the area of

wave generation. The length of the fetch influence on

characteristics of wave, when fetch is getting longer

it will be formed waves with periods of great.

In the form of irregular power, generation areas,

then the calculations can be done effectively fetch and

then the results will be used to predict the

characteristics of waves in the deep ocean.

4 RESULT

4.1 Wind

Wind data analysis is conducted to find out the

dominant wind direction and the number of

occurrences of the wind according to directions. After

wind data obtained, then wind data processed to be

classified. The classified data shows the genesis Wind

around the coast of the estuary of Kali Porong for year

period of 2011-2015 in the shape of event frequency

and percentage respectively.

Wave Analysisi in near Shoreline for Coastal Morphology in Mouth of Kali Porong Sidoarjo

191

It also can be seen that the dominant wind

direction blows from the southeast with the number

of events 13927, with a percentage of 31.785% of all

events in a period of 5 years. The data above can be

presented in the form of a rose wind. Figure 2 shows

the Rose of the Wind (Tanjung Perak of Maritime

Meteorology Station (2011 - 2015).

Figure 2: Rose of the Wind (Tanjung Perak of Maritime

Meteorology Station 2011-2015).

4.2 Fetch

After the analysis of wind, data and the direction of

the dominant wind are obtained, and then the fetch

length is calculated (length of wave generation area).

Fetch will be longer, a wave with a large period will

be formed. In this research, the biggest fetch become

the dominant wind direction. Therefore, this

calculation uses the fetch of the dominant east

direction. When the waveform generation area is

irregular, then for effective fetch calculation can be

done equation (1) below (Triatmojo, 1999):

eff

F 65.161968

cos









(15)

With:

Feff = fetch effective

Xi = fetch-th line length

αi = deviation on both sides of the wind direction,

dominant by using an increment of 6 ° to an angle of

42 ° on both sides of the dominant wind direction.

Figure 3 shows the map for Effective Fetch

Length Calculation. Fetch effective calculation

results have be presented in table 1.

Table 1: Fetch Effective calculations.

a cos a X

(km) X

cos a

42 0,74 117,05 86,98

36 0,81 140,47 113,64

30 0,87 126,10 109,21

24 0,91 173,90 158,86

18 0,95 250,00 237,76

12 0,98 250,00 244,54

6 0,99 250,00 248,63

0 1,00 250,00 250,00

6 0,99 250,00 248,63

12 0,98 127,32 124,54

18 0,95 111,67 106,20

24 0,91 97,54 89,10

30 0,87 73,32 63,50

36 0,81 70,84 57,31

42 0,74 66,51 49,43

∑ 13,51 2188,35

eff

= 161,97 km 161968,65 m

Figure 3: Map for Effective Fetch Length Calculation.

The value of α0 is the dominant wind direction,

where the study uses the second dominant wind

direction (East) because the fetch is greater than the

direction of the first dominant wind direction. Xi is

the distance from the study location to the nearest

land. Likewise for other angles. After obtaining the

distance for each angle, the effective fetch from the

calculation using equation (1) is 161.96865 km. The

next step is to change the data from the land recording

(UL) to the sea wind speed data (Uw) to find the value

of RL that can be obtained by plotting UL values into

the characteristic graph. Then to calculate the H0, T0,

Hrms, Trms, H1/3, T1/3, could be used the

formulation of 2 till 7. Table 2 and 3 show the result

of the calculation.

ISOCEEN 2018 - 6th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management

192

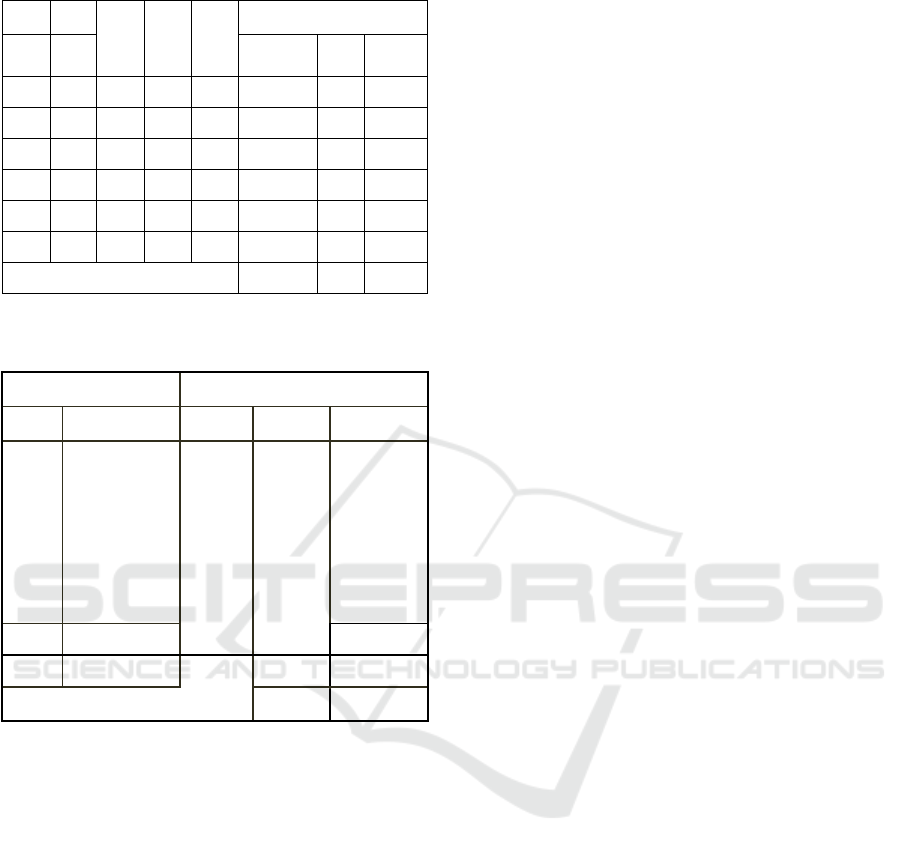
Table 2: The calculation of H0 and T0.

315

Knots m/s m/s m/s F eff (m)

(m)

(s)

2,06 1,68 3,46 3,27 161968,65 0,67 4,83

3,61 1,47 5,30 5,52 161968,65 1,14 5,74

11 5,67 1,31 7,42 8,35 161968,65 1,72 6,58

17 8,76 1,13 9,89 11,90 161968,65 2,45 7,40

21 10,82 1,05 11,36 14,10 161968,65 2,90 7,82

22 11,33 1,04 11,78 14,75 161968,65 3,04 7,94

∑ 8,88 32,37

Table 3: The calculation of Hrms (Significant wave height)

and T1/3 (Significant wave period).

0 1/3

(m) = 1.42 x Hrms

n x H

(m)

Hrms

0 1/3

(m) n x T

(s)

28889 13068,81

0,8840 1,2553

673878,62

12342 15925,85 406869,50

1361 4021,12 58972,88

52 311,64 2845,52

0 0,00 0,00

42644 33327,41 1142566,52

Hrms 0,88404

Trms

5,1762

0 1/3

(s)

7,3502

From the calculation results in Table 2, the values

of H1/3 and T1/3 are 1.26 meters and 7.35 seconds,

next for analysis of; Refraction, Shoaling, and

Breaking Waves. To perform analysis of refraction,

shoaling, and breaking waves used calculations in

Excel programs.

4.3 Breaking Wave

For analysis of; shoaling, refraction, and breaking

waves the input and assumptions used are one (1.0).

The wave data used is significant wave data obtained

from wind wave forecasting (Table 2). Coastal slope

is obtained from the height difference between

contours being reviewed divided by the distance

between the depth contours obtained from the

bathymetry map, which is then processed in the

AutoCAD system. The wave direction of calculated

result is from the Southeast. The seabed contour is

considered parallel to the coastline.

The study area have been divided become three

slices in order to calculate the slope. These calculated

slopes for each slice are; 0.0064, 0.0046, and 0.0018.

The largest distance of breaking wave from these

three slices is around it that about 1200 meter from

the shoreline perpendicular to the offshore direction.

5 DISCUSSION

Regarding to the East of dominant wind direction, the

distance as fetch effective for this direction is limited

to 250 km as a maximum fetch due to no boundary

such as island. The result of H1/3 and T1/3 are 1.26

meters and 7.35 seconds is a typical for the Madura

Strait. Annually, this dominant wind will create the

wave that furthermore to produce the near shoreline

current that have parallel direction to the shoreline.

This current normally called long shore current. In

this case, of shoreline profile, the long shore current

will flow from South to North direction.

Related to the breaking wave, the slope of

bathymetry causes the range of distance where the

breaking wave wills accordance. This research area

have been divided become three slices. These slopes

for each slice are; 0.0064, 0.0046, and 0.0018. The

distance furthest of breaking wave from these three

slices is around 1200 meter from the shoreline

perpendicular to the offshore direction. On the other

hand, the nearest distance of breaking wave from

these three slices is gradually difference the bigger of

slope the nearest distance. The largest slope, i.e.

0.0064 makes nearest distance of breaking wave of

200 meter from the shoreline perpendicular to the

offshore direction. While the smallest slope, i.e.

0.0018 makes shortest distance of breaking wave of

680 meter from the shoreline perpendicular to the

offshore direction as well. This information may

useful for related stakeholders, for instance; to

designer of coastal eco-truism planning, to local

fisheries for finding the certain fish (Mustain, et.al,

2015; Mustain, 2016; Fauzi, et.al, 2017; Mustain,

et.al, 2018).

6 CONCLUSION

The results of the analysis and calculations have been

carried out; some conclusions can be drawn as

follows:

1. The dominant wind direction in the study used in

the effective fetch calculation is the east dominant

Wave Analysisi in near Shoreline for Coastal Morphology in Mouth of Kali Porong Sidoarjo

193

direction with the effective fetch value in this

research location at 161.96865 km.

2. Significant wave height H1/3 and (significant wave

period) T1/3 at the location of this study is 1.26

meters and 7.35 seconds.

3. The height of the breaking wave for slice 1 is

1.5459 meters with a breaking wave depth of 1.8989

m; the height of the wave breaking for slice 2

amounting to 1.5458 meters with a breaking wave

depth of 1.9181 m, the breaking wave height for slice

3 is 1.5458 meters with a breaking wave depth of

1.9578 m.

ACKNOWLEDGEMENTS

The authors thank the Directorate of Empowering of

smaller islands, Directorate General Ocean and Small

Islands of the Ministry of Fisheries on support of

provided data up to this paper then could be finished

very well. This research was also supported by the

Minister of Research and Technology (Indonesia) and

LPPM-ITS. Therefore, the authors thank and

appreciate both institutions for the funds.

REFERENCES

B. Triatmodjo, 1999. Teknik Pantai, Beta Offset,

Yogyakarta.

CERC., 1984. Shore Protection Manual Volume I * II.U.S

Army, Coastal Engineering Research Centre,

Washington.

D. N. Sugianto, 2010. Maritime. Jour. 15, 3, 143-152.

M. Mustain, A. Sufyan, R. Akhwady, 2018. Int. Jour.

Civ.Eng- Techn. (IJCIET), 9, 2, 565–576.

M. Mustain, 2016. Jour. Appl. Mech.-Mate. (AMM), 836,

236, 239-244.

M. Mustain, 2017. Int. Jour. Eng-Appl. Sci. (IJEAS), 4, 11.

M. Mustain, 2018. Int. Jour. Civ.Eng- Techn. (IJCIET), 9,

1, 688–701.

M. Mustain, D.A. Haryo, T. K. Danu, 2015. Proc. Earth-

Plan.Sci., 17-24.

M. Mustain, R. I. Salim, Sholihin, Sujantoko, 2010. IPTEK,

Jour. Tech. Sci. 21, 7.

M. A. R., Fauzi, D. A. Haryo, M. Mustain, A.R. Amalia,

2017. The Third International Conference on Civil

Engineering Research (ICCER), Surabaya-Indonesia.

W. A. Pratikto, 1996. Coastal Protection Structure, ITS FTK

Surabaya.

ISOCEEN 2018 - 6th International Seminar on Ocean and Coastal Engineering, Environmental and Natural Disaster Management

194