Discovery Learning Model for Solving System of Linear Equations

using GeoGebra

Isnaini Rambe

, M. R. Syahputra

, Dhia Octariani

, Asnawati Matondang

Mathematics Education, Faculty of Teacher Training and Education, Universitas Islam Sumatera Utara, Indonesia

Department of Mathematics, Faculty of Mathematics and Natural Sciences, Universitas Sumatera Utara, Indonesia

Keywords: Discovery learning model, geogebra.

Abstract: In this paper, the authors introduce a discovery learning model to increase students' interest in learning.

Software that supports the learning process using this discovery model is GeoGebra. This study introduces

how to solve system problems in linear equations, both two variables and three variables interactively. From

the results of observations as many as 5 times carried out on third grade students in junior high school in

Bhayangkari Medan, showed a significant increase in learning interest. The average of student activity at the

beginning is 84.04% with good category. While in the main activity, the average of students’ activity on (i)

contextual understanding is 95.98% with very good category, (ii) Developing mathematical model is

85.14% with good category, (iii) constructing a program is 89.12% with very good category, (iv)

interactivity is 96.02% with very good category; (v) interest is 90.84% with very good category. For the

final activity, the average of student activity in making conclusion is 94.28% with very good category.

Overall, the total average of the observation is 90.77%. This means that the seriousness and interest in

student learning has increased.

1 INTRODUCTION

Mathematics has a field of study whose object is

abstract. This may be the reason why many people

find it difficult to understand the concepts in

mathematics. Due to the mathematics become one of

the most important subject in the curriculum at the

school, while many people are still having trouble

then it is necessary to help students to understand the

concepts of mathematics. In this era, technology has

become an integral part of human life. This is

because the benefits provided, in particular in the

field of education.

Technology is used as a medium that can assist

teachers in learning activities at school, especially in

mathematics. For example, when the teacher would

sketch geometry. Sometimes teachers will find it

difficult to sketch directly. But with the use of

technology, issues like that will be easy. In addition,

the use of technology in learning mathematics can

also be used for some of the following, (Naidoo and

Jayaluxmi, 2010).

1. Assist the process of understanding the

concept.

2. Help strengthen students’ memory about the

concepts.

3. Increase student interest and appreciation of

the concepts that has been learned.

Technological developments quickly become one

focus of which will be developed in the curriculum

2013. One of the principles of learning in the

curriculum 2013 is the utilization of information and

communication technologies to improve the

efficiency and effectiveness of learning. In other

words, technology should be integrated in each

learning and the technology used must also be

adapted to the situation and learning conditions. For

that teachers are expected to use technology to

support math learning activities so that the learning

environment becomes active and fun. In this study,

the authors use a computer as a learning medium.

The use of computers as a medium of learning in

mathematics aims to support students in

understanding the concepts in mathematics.

The computer program used in this study is

GeoGebra. GeoGebra developed by Markus

Hohenwarter in 2001. (Chrysanthou, 2008) revealed

that GeoGebra influences the educational practice in

Rambe, I., Syahputra, M., Octariani, D. and Matondang, A.

Discovery Learning Model for Solving System of Linear Equations using GeoGebra.

DOI: 10.5220/0008885503830386

In Proceedings of the 7th International Conference on Multidisciplinary Research (ICMR 2018) - , pages 383-386

ISBN: 978-989-758-437-4

383

three dimensions, namely: classroom practice,

cognitive development and learning attitudes.

Correspondingly, Ali Gunay Balim (2009) revealed

that GeoGebra is able to present an overview so that

students can understand the material. Use of

GeoGebra is very easy. Given interface makes the

students more interested in the subject presented by

the teacher.

2 DISCOVERY LEARNING

MODEL

Discovery learning model is defined as a learning

process that occurs when students are not presented

with a lesson in its final form, but is expected to

organize themselves. It is more emphasis on the

discovery of concepts or principles that were

previously unknown.

In applying the discovery learning model,

teachers act as mentors by providing opportunities

for students to learn actively, the teacher should be

able to guide directly the learning activities of

students in accordance with the purpose. Conditions

such as these will change the teaching and learning

activities from teacher-oriented to student oriented.

The following are the phases in the discovery

learning model:

1. Stimulation. Teachers raise the question or ask

the students to read or hear a description that

includes the issue.

2. Problem Statement. The students were given the

opportunity to identify problems and formulated

in the form of a question or hypothesis.

3. Data Collection. To answer a question or to

prove the hypothesis, the students were given the

opportunity to collect data and information

needed.

4. Data Processing. Event processing data and

information has been obtained by the students,

and then interpreted.

5. Verification. Based on the results of processing

and Opera-existing hypotheses formulated

question should be checked beforehand. Can it

be missed or well proven that the results are

satisfactory.

6. Generalization. In this last phase the students

learn to draw certain conclusions and

generalizations.

Illahi (2012).

A basic concept of discovery learning is that

teachers should facilitate instruction that allows

students to discover predetermined outcomes

according to the level of learning required by the

curriculum 2013, Mandrin and Preckel (2009).

Hopefully, students will pose relevant questions

such as "what if the variables is fewer than the

system?" or "what if the coefficient is the multiple of

other systems?" Discovery learning allows for

deeper thought into the subject.

As an introductory activity, the teacher, acting as

facilitator, should prompt students to recall

knowledge and experiences from previous lessons,

and encourage student participation. The teacher

should then guide students in applying already

existing knowledge to new information to construct

deeper levels of meaning and understanding. This

gives students an active opportunity to apply what

they already know about the topic to the new

situation, (Schunk, 2008).

After introducing the purpose of the lesson, the

teacher describes the materials that will be used in

the experiment and then models the actions and

procedures for the students, GTC (2006). Students

begin the actual lesson by asking questions, guided

by the teacher prompts, and then try to guess at

possible right answers.

3 SYSTEM OF LINEAR

EQUATIONS

In mathematics, a system of linear equations is a

group of two or more linear equations that involving

the same set of variables. For an example, The

following is a linear system of three equations

consisting of three variables

4𝑥 − 2𝑦 − 3𝑧 = 6

5𝑥 + 3𝑦 − 4𝑧 = 2

−𝑥 − 𝑦 + 2𝑧 = 0

(1)

A unique solution to that linear system is an

assignment of values to the variables such that all

the equations are simultaneously satisfied. A

solution to the linear system above is given by 𝑥 =

1, 𝑦 = −1, 𝑧 = 0. since there’s no other solution,

the solution is said to be unique solution. Since the

solution set value of (x, y and z) of this problem is

satisfy the equation, the word system indicates that

all the three equations are to be considered

collectively, rather than individually indeed.

The role of technology will be needed in solving

the problem of linear systems that have many

equations. The theory of linear systems is the basis

and a fundamental part of linear algebra.

Computational algorithms for finding the solutions

ICMR 2018 - International Conference on Multidisciplinary Research

384

are an important part of numerical linear algebra,

and play an important role in computer science,

economics, engineering, physics and also chemistry.

Solving a problem computationally will be even

better if able to provide a visual solution. So that,

students’ interest in lessons will increase.

The following is one of three possibilities of the

solution set in the linear system:

1. It has infinitely many solutions.

2. It has an unique solution.

3. It has no solution.

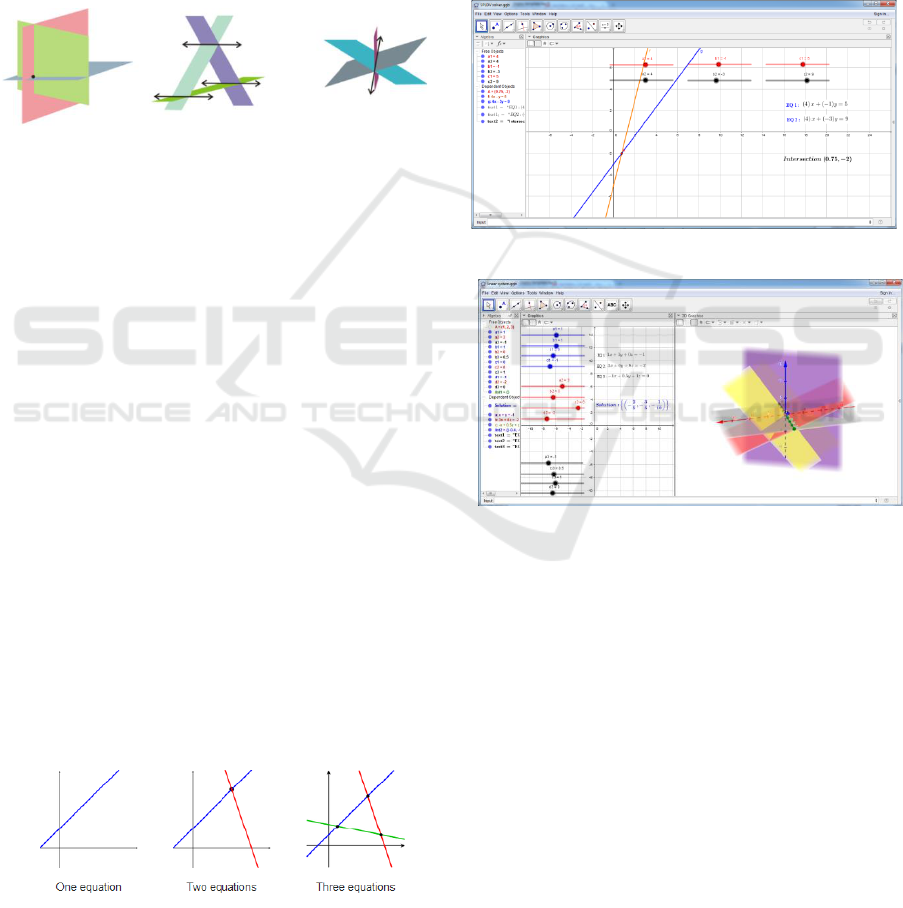
Figure 1: Solution set of linear System.

3.1 General Behaviour of System of

Linear Equations

A linear equation system is determined by the

relationship between the number of equations and

the number of variables. The following is one of

three possibilities of a common problem.

1. A system with more variables than equations has

infinitely many solutions, but it may have no

solution. It is also known as an underdetermined

system.

2. A system with the same number of variables and

equations has a single unique solution.

3. A system with fewer variables than equations has

no solution. It is also known as an over-

determined system.

In the first case, the dimension of the solution set

is usually equal to n-m, where n is the number of

variables and m is the number of equations. Figure 2

illustrate this tracheotomy in the case of two

variables.

Figure 2: Trichotomy of solution of linear system with two

variables.

3.2 Solving Linear System using

GeoGebra

There are some methods that can be use to solving a

linear system, such as: elimination, substitution,

crammer’s rule, row reduction and etc. However,

this study introduces GeoGebra as a tool for solving

linear system.

Figure 3: GeoGebra interface of linear equation system

with two variables.

Figure 4: GeoGebra interface of linear equation system

with three variables.

With the help of Geogebra, students’ curiosity

will be well stimulated. It is because GeoGebra is

able to provide visualization of the given problem.

So that students no longer have difficulties in

understanding the concept of linear equation system

problem.

Students will be able to immediately know the

relationship between coefficients and equations to

the solution of the problem. This is because the

program created authors interactively. Students can

change the coefficient and constant values in the

equation by moving the slider, and simultaneously

also can see the shift of the curve formed. Thus,

students are expected to further understand the

concept of linear equation system problems.

Discovery Learning Model for Solving System of Linear Equations using GeoGebra

385

4 OBSERVATION RESULT

Observations were carried out 5 times for third grade

students in junior high school in SMP Bhayangkari

Medan. The following is an analysis of the results of

observation of student learning improvement using

discovery learning model with GeoGebra.

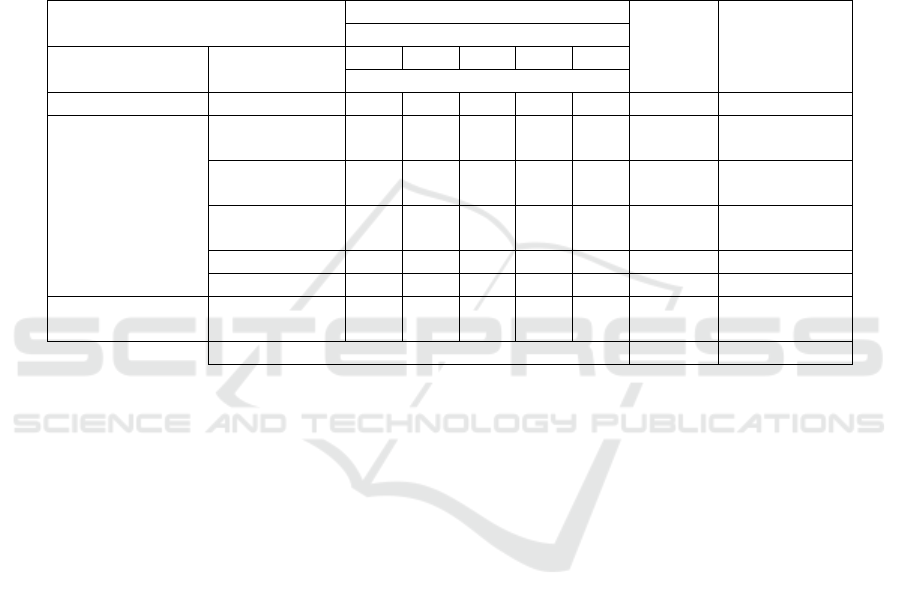
Based on Table 1, it can be seen that the average

of student activity at the beginning is 84.04% with

good category. While in the main activity, the

average of students’ activity on (i) contextual

understanding is 95.98% with very good category,

(ii) Developing mathematical model is 85.14% with

good category, (iii) constructing a program is

89.12% with very good category, (iv) inter-activity

is 96.02% with very good category, (v) interest is

90.84% with very good category. For the final

activity, the average of student activity in making

conclusion is 94.28% with very good category.

Table 1: Students’ learning improvement.

Category of Observation

Activity Observation

Average

(%)

Category of

Assessment

Session

Phase of Activity

Indicator

Score (%)

Beginning

Preparation

68.6

71.4

85.7

94.3

100

84.04

Good

Main

Contextual

Understanding

85.7

97.1

100

95.98

Very Good

Developing a

Math Model

82.9

91.4

85.7

85.14

Good

Constructing a

Program

71.4

97.1

100

97.1

89.12

Very Good

Interactivity

85.7

97.2

100

96.02

Very Good

Interest

85.7

91.4

97.1

100

90.84

Very Good

Closing

Making

Conclusion

85.7

94.3

97.1

100

94.28

Very Good

Total Average of Observation

90.77

Very Good

From the explanation it can be concluded that

the application of discovery learning model on

solving linear equation system using GeoGebra is

very helpful for students to better understand the

concept of lesson. In addition, students’ interest in

mathematics will increase as well. Overall, students

have a good improvement from all aspects.

5 CONCLUSION

As discussed in this paper, it can be concluded as

follows:

1. Discovery learning model is very helpful for

students to understand the concept, build self-

confidence, and able to improve students’

learning ability well.

2. From the results of observations five times, it

can be concluded that the use of GeGebra in

discovery learning models, especially in

learning systems of linear equations, can help

increase students' interest in learning. This can

be seen from the total value of the average

observation is 90.77%.

REFERENCES

Balim, A. G., 2009. The Effects of Discovery Learning on

Students’ Success and Inquiry Learning Skills.

Eurasian Journal of Educational Research, Issue 35,

Spring 2009, 1-20.

Chrysanthou, I., 2008. The Use of ICT In Primary

Mathematics In Cyprus: The Case Of GeoGebra.

Thesis. University of Cambridge.

General Teaching Council for England (GTC)., 2006.

Research for teachers. Jerome Bruner’s constructivist

model and the spiral curriculum for teaching and

learning.

Illahi, M. T., 2012. Strategy of Discovery Learining &

Mental Vocational Skill. Jogjakarta: DIVA Press.

Mandrin, P.A. & Preckel, D., 2009. Effect of similarity

based guided discovery learning on conceptual

performance. School Science and Mathematics. 109

(3).

Naidoo and Jayaluxmi., 2010. Strategies Used by Grade

12 Mathematics Learners in Transformation

Geometry. Proceedings of the 18th Annual Meeting of

the Southern Africa Association for Research in

Mathematics, Science, and Technology Education.

Schunk, D.H., 2008. Learning theories (5th ed.). Upper

Saddle River, NJ: Pearson Education, Inc.

ICMR 2018 - International Conference on Multidisciplinary Research

386