Improvement of College Students Mathematical Concept

Understanding through DNR-based Instruction Models

Marwia Tamrin Bakar

, Didi Suryadi

and Darhim

Mathematics Education Study Program, Universitas Khairun, Indonesia

Mathematics Education Department, Universitas Pendidikan Indonesia, Indonesia

Keywords: DNR-Based Instruction, Mathematical concept understanding, Mathematics education.

Abstract: Mathematical concept understanding is the basic ability that students must possess in learning mathematics.

Mathematics that is abstract, having symbols which can be only understood in its field, makes mathematics

complicated as felt by some students. The DNR-Based Instruction model with the principles of duality,

necessity and repeated reasoning can improve students' ability to understand mathematical concepts.

Therefore this study aims to determine the improvement in students' mathematical concept understanding

through the DNR-Based Instruction model. Descriptive and n-gain analysis was used to analyze the results

of students' work at pretest and posttest and then to discover the amount and qualification of the

improvement in 54 students at a state university in North Maluku Indonesia. The results showed that there

was an increase in students' mathematical concept understanding of 0.66 with moderate qualifications. The

implication of this research is that learning mathematics by emphasizing on concept understanding is a way

in which mathematics should be taught.

1 INTRODUCTION

Understanding mathematics is not only about

remembering concepts (Godino, J. D, 1996), or

being able to follow procedures (Idris, N, 2009).

Understanding the mathematical concept is a deeper

understanding and understanding of the basic nature

of mathematics, from simple facts to mathematical

proof which are all indicators of mathematical

understanding (Hoosain, E., 2001). Understanding

mathematical concepts is the basis for developing

other mathematical abilities (Bakar, 2018b).

Understanding mathematical concepts means

knowing the concept in depth, being able to

interpret, explain, prove and apply it in problem

solving. The activities of understanding mathematics

such as interpreting, concluding, proving,

explaining, composing, predicting, applying,

classifying, generalizing and solving problems are

mental actions that are performed not only in this

area of subject but also daily life (Bakar, 2018a).

Research related to understanding concepts has

been widely carried out, for example by Bakar

(2018b); Bakar (2018); Kieran (1994); Fuadi (2016)

which broadly states that students’ concept

understanding is still low and it is still difficult for

them to think deeply. Attorps (2006) stated that

many college students experienced problems with

mathematical concepts and symbols. The results of

(Bakar, 2018a) research in the early semester

students related to the basic concepts of mathematics

show that most students make mistakes in

interpreting the problem due to the lack of concept

understanding and weak reasoning in understanding

the problem.

The DNR-Based Instruction model, hereinafter

referred to as DNR-BI, is considered to be able to

improve students' ability to understand mathematical

concepts because this learning model emphasizes on

the intellectual needs of students in mathematics and

how mathematics should be taught.

2 METHOD

This study aims to discover and describe the

achievement and improvement of the mathematical

concept understanding ability of students who obtain

DNR-BI learning method. The subjects were fifty-

four elementary pre-service student teachers at a

state university in Ternate, North Maluku,

Indonesia, who attended lectures on Basic

190

Bakar, M., Suryadi, D. and Darhim, .

Improvement of College Students Mathematical Concept Understanding through DNR-based Instruction Models.

DOI: 10.5220/0008899101900193

In Proceedings of the 1st International Conference on Teaching and Learning (ICTL 2018), pages 190-193

ISBN: 978-989-758-439-8

Mathematical Concepts. The pre-test and post-test

questions used were arranged based on the indicators

of concept understanding. The indicators of

understanding the mathematical concept are being

able to associate a concept with other concepts,

representing mathematical situations in various

ways, and being able to determine a more

appropriate representation. The four questions used

in this article were questions that have been

published in our previous article (See Bakar 2018a)

but with a different analysis. The four questions are

presented in Table 1 below:

Table 1: Problem description.

o. Problems

Mr. Amir bought five recreational park tickets for two adults and three children for

Rp105,000.00 Meanwhile Pak Iksan bought three tickets for adults and five tickets for

children at Rp165,000.00 State this situation in the most appropriate form you think (among

SPLDV settlement methods) to determine the price of each recreational park ticket.

A convenience store sells two types of rice. Rice type I and rice type II. The price of rice type

I is Rp 10,000.00 and the price of rice type II is Rp. 13,000.00. The sales on that day were Rp.

2,935,000.00 and the amount of rice sold were as much as 250 litres.

a. What kind of rice is the bestseller? Explain your reasons.

b. Suppose that rice sold for 370 and sales were of Rp 4,450,000.00. How much is each type

of rice sold?

c. What conclusions are derived from these two problems?

The circumference of an isosceles triangle is 20 cm. If the length of both feet added by 3 cm

and the length of the base two times the original length then the circumference to be 34 cm.

Represent your answers using more than two ways to get the lengths of all three sides of the

isosceles triangle.

A rectangular object with a circumference of 22 cm. If the length is made to three times the

original length and width are made twice the original width, then the circumferences of the

ect

ecome 58 cm. Find the area of the rectan

le and explain the answers

et.

Analysis of achievement and improvement of

students' mathematical concept ability using

descriptive analysis and normalized gain formula

developed by Harel, G (2001). The results of the

normalized gain calculation were then interpreted

using the classification stated by Hake, R. R.

(1999). These interpretations and classifications

are presented in Table 2 below:

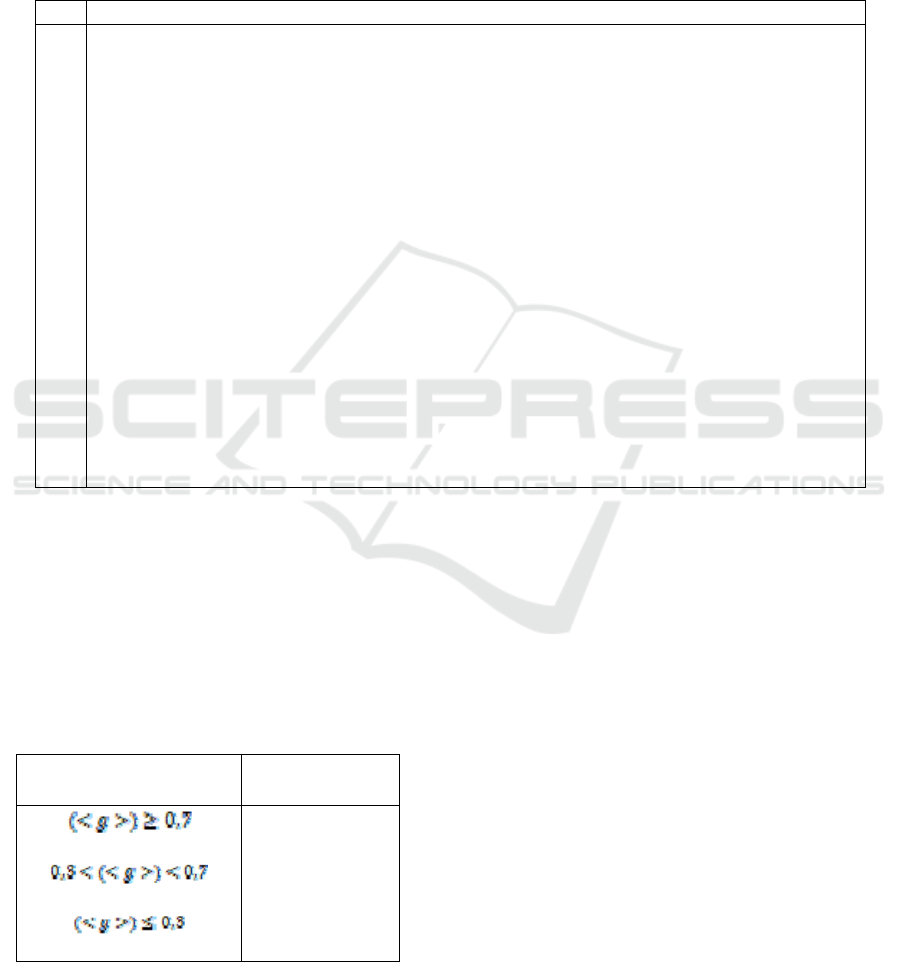
Table 2: Normalized Gain Classification.

N-Gain Value (g) Interpretation

High

Medium

Low

3 RESULT

Descriptively data regarding the achievement

ability to understand mathematical concepts of

fifty-four students who received DNR-Based

Instruction as a whole obtained an average of

78.055 with a standard deviation of 7.87 and a

variation coefficient of 10.08%. This means that

the contribution of lectures by using the DNR-

Based Instruction model is better to establish

students' understanding on mathematical concepts.

In other words, students who are applied to the

DNR-Based Instruction model in the Basic

Mathematics Concept lecture get more benefits and

get the opportunity to explore knowledge during

lectures. For example, it was shown from the

results of student’s paperwork in solving the

system problems of two variables in the form of

story problems as shown in Figure 1:

Improvement of College Students Mathematical Concept Understanding through DNR-based Instruction Models

191

Figure 1: One of Students’ Paperwork.

Overall, the results of test in increasing students’

(primary school teacher candidates) understanding

towards mathematical concepts descriptively

showed that pre-test score of 36, 38 and post-test

of 78.055 with an ideal maximum score of 100 and

obtained normalized gain of 0.66 based on Hake

normalized gain classification, in Table 1 is

categorized as medium.

4 DISCUSSION

The level of the students’ achievement and

improvement in understanding mathematical

concepts who obtain DNR-Based Instruction

learning in solving problems related to a two-

variable liner equation system with an average of

78.055 and a standard deviation of 7.87 with an n-

gain of 0.66 with a medium increase category

shows that learning by using the DNR-Based

Instruction model has a positive effect on

achieving and improving students' mathematical

concepts understanding. The high contribution of

the DNR-Based Instruction learning models is

because the DNR-Based Instruction model has the

principles of duality, necessity and repeated

reasoning (Harel 2008a) which emphasizes the

mastery of content and student’s intellectual needs.

Duality principle considers that mathematics

understanding and thinking method, which is

called as Ways of Understanding (WoU) and Ways

of Thinking (WoT) (Harel 2008b). This principle

requires learning mathematics not only in

mastering concepts, theorems, evidence, rules etc.,

but it also directs learner to master the way of

thinking.

Furthermore, the necessity principle states

that students will be interested in teacher’s

teaching if they find a necessity on the teaching

materials. Therefore, the DNR-Based Instruction

model highly regards on meeting student’s

intellectual needs (Harel 2010) Presenting and

marking student’s intellectual needs are indeed

difficult to do, but it does not mean that it is

improbable. There will be differences in teaching

methods or approach between teachers who have

the knowledge of teaching and mastering math

content with teachers who do not have that

knowledge. The principle of repeated reasoning

considers that repetition in mathematic learning

activities will improve student’s

concept/knowledge of mathematics. However

repeated reasoning is different with working on

repeated examples. Repeated reasoning

emphasizes on thinking method (Harel; 2001).

Thus the DNR-Based instruction model is a

learning model that strongly emphasizes the

aspects of mastering mathematical concepts, not on

the psychological aspects.

5 CONCLUSION

Achievement and improvement of students'

understanding towards mathematical concepts can

be improved through the DNR-Based Instruction

model, with an average achievement of 78.055.

Improvement value is categorized under the

average category.

ACKNOWLEDGEMENTS

Sincere gratitude would like to be given to the

students of Elementary School Teacher Education

Study Program, Ternate Khairun University who

were cooperating with this research activity.

REFERENCES

Godino, J. D., 1996. Mathematical Concepts, Their

Meanings, and Understanding. In Proceedings

of XX Conference of the International Group for

the Psychology of Mathematics Education. V.2,

pp. 417 – 425. Universidad de Valencia.

Idris, N., 2009. Enhancing Students’ Understanding in

Calculus through Writing International Electronic

Journal of Mathematics Education 4 1

Hoosain, E., 2001. What Does It Mean to Understand

Mathematics?, Humanistic Mathematics

Network Journal, 25, 9

Bakar, 2018b. Mathematical Concept Understanding,

Reasoning, and Disposition Ability Improvement on

Students of Elementary Teacher Education

ICTL 2018 - The 1st International Conference on Teaching and Learning

192

Program through DNR- Based Instruction Model

- Disertation

Bakar, 2018a. The association between conceptual

understanding and reasoning ability in

mathematics: An analysis of DNR-based

instruction models. IOP Conf. Series: Journal of

Physics: Conf. Series 1088 2018 012107. Doi

10.1088/1742-6596/1088/012107

Bakar, 2018. Learning Obstacles on Linear Aquation

concept in Junior High school Students: Analysis of

Intellectual Need of DNR-Based Instructions.

(in reviuw) IOP Conf, series: Journal Physics

Kieran, C., 1994. Doing and seeing things differently: A

25-year retrospective of mathematics education

research on learning. ”Journal for Research

in Mathematics Education 25 583-687

Fuadi, R., Johar, R., & Munzir, S., 2016. Improving the

ability of Mathematical Understanding and

Reasoning through Contextual Approach

Juornal Didaktika Matematika 3 1

Attorps, I., 2006. Mathematics Teachers’ Conception

about Equations. Thesis. University of

Helsinki, Fakulty of Behaviour Sciences

Department of Applied Education

Harel, G. 2001. The development of mathematical

induction as a proof scheme: A model for

DNR-Based instruction. In S. Campbell & R.

Zaskis (Eds.), Learning and teaching number

theory. In C. Maher (Ed.), Journal of

Mathematical Behavior. New Jersey, Ablex

Publishing Corporation, 185–212.

Hake, R. R. 1999. Analyzing Change/Gain Score.

Departement of Physics. Woodland Hills USA:

Indiana University.

Harel, G., 2008a. DNR perspective on mathematics

curriculum and instruction, Part II: With reference to

teacher’s knowledge base. Zentralblatt f¨ur

Didaktik der Mathematik, 40, 893– 907.

Harel, G., 2008. What is mathematics? A Pedagogical

answer to a philosophical question. In R. B.

Gold & R. Simons (Eds.), Proof and other

dilemmas: Mathematics and philosophy (pp. 265–

290). Washington, DC: Mathematical

Association of America

Harel, G., 2013. Intellectual Need, in Keith R. Leatham.

Vital Direction for Mathematics Education

Research (pp. 119- 151). New York Springer.

Harel, G., 2007. The DNR System as a Conceptual

Framework for Curriculum Development and

Instruction. In R. Lesh, J. Kaput & E. Hamilton

(Eds.), Foundations for the Future in Mathematics

Education. Erlbaum.

Improvement of College Students Mathematical Concept Understanding through DNR-based Instruction Models

193